В координатной плоскости xoy линия задана уравнением

Контрольно — измерительные материалы по дисциплине «ЭЛЕМЕНТЫ ВЫСШЕЙ МАТЕМАТИКИ» для специальности среднего профессионального образования Компьютерные сети

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

ПО ДИСЦИПЛИНЕ «ЭЛЕМЕНТЫ ВЫСШЕЙ МАТЕМАТИКИ»

для специальности среднего профессионального образования

09.02.02 «Компьютерные сети »

Разработал преподаватель математики

ГБПОУ СПО Ханнанова Э. А.

А 1. Если А и В=, то матрица С=2А+В имеет вид…

А 2. Найти произведение матриц

А 3. Если определитель второго порядка =11, то х=

a ) 0 b ) 6 c ) -6 d ) 1

А 4. Определитель равен …

a ) 0 b ) 12 c ) 10 d ) 1

А 5. Решите систему

a ) (2; 3) b ) (1;2) c ) (3; 2) d ) (-2; 3)

А 6. Система линейных уравнений имеет решение …

a ) x =-2; у=1; z =4 b ) x =-2; у=1; z =-4 c ) x =-2; у=-1; z =4 d ) x =2; у=1; z =4

А 7. Для точек А (3; -9) и В(2; -5) уравнение прямой может быть записано в виде …

a ) у=-4х+3 b ) у=-2х-3 c ) у=х-7 d ) у=3х+6

А 8. Укажите правильное соответствие между уравнением и типами уравнений прямой на плоскости 2х-5 y -9=0

a ) уравнение прямой с угловым коэффициентом

b ) уравнение прямой в отрезках

c ) каноническое уравнение прямой

d ) общее уравнение прямой

А 9. Нормальным вектором прямой х-2у+3=0 является вектор:

a ) (-2;1); b ) (-2;3); c ) (3;-2); d ) (1;-2)

А 10. Прямая проходит через точки О(0;0) и В(-2;1). Тогда ее угловой коэффициент равен:

a ) ; b ) 2; c ) ; d ) -2

А 11. В координатной плоскости XOY линия задана уравнением х 2 +у 2 =169. Тогда эта линия проходит через точки …

a ) (5; -12) и (-12; 3) b ) (-13;0) и (5; -12); c ) (6;-11) и (5; -12) d ) (12;3) и (5; -12)

А 12. Укажите соответствие между кривой второго порядка и их уравнениями
(х+6) 2 +(у-2) 2 =64

a ) парабола b ) гипербола c ) эллипс d ) окружность

А 13. Если уравнение гиперболы имеет вид , то длина ее действительной полуоси равна…

a ) 16 b ) 3 c ) 9 d ) 4

А 14. Вычислить предел функции:

a ) 7; b ) 4; c ) 13; d ) – 4

А 15. Число точек разрыва функции равно…

a ) 2 b ) 1 c ) 3 d ) 0

А 16. Производная функции у = cos 5 x имеет вид:

a) cos 5x; b) -5sin5x; c) — 5sinx; d) 5cos5x

А 17. Найти производную от функции, заданной параметрически:

a ) -2 t -2; b ) 2 t +2; c ) -; d )

А 18. Найти частную производную функции

a) 3x 2 ; b) 2y; c) 3x 2 + 2y; d) 3x 2 — 2y

А 19. Вычислить предел:

a ) 2 b ) -2 c ) 1 d ) 4

А 20. Определенный интеграл равен

a ) 54; b ); c ) 26; d )

А 1. Если А и В=, то матрица С=3А+В имеет вид…

А 2. Найти произведение матриц

А3. Если определитель второго порядка =1, то х= …

a ) -8 b ) 8 c ) 7 d ) -7

А 4. Определитель равен …

a ) 0 b ) 1 c ) 3 d ) 4

А 5. Решите систему

a ) (2; 3) b ) (7; 1) c ) (1; 7) d ) (-2; 3)

А 6. Система линейных уравнений имеет решение …

a ) x =3; у=2; z =1 b ) x =3; у=-2; z =1 c ) x =3; у=2; z =-1 d ) x =-3; у=2; z =1

А 7. Для точек А(-4;-2) и В(2;-6) уравнением прямой является …

a ) 3х+2у+14=0 b ) 2х+3у+14=0 c ) 3х+у+7=0 d ) х+3у+14=0

А 8. Укажите правильное соответствие между уравнением и типами уравнений прямой на плоскости y =-3 x +7

a ) параметрическое уравнение прямой

b ) уравнение прямой с угловым коэффициентом

c ) уравнение прямой в отрезках

d ) общее уравнение прямой

А 9. Нормальным вектором прямой 2х-3у+5=0 является вектор:

a ) (-3;2); b ) (-3;5); c ) (2;-3;5); d ) (2;-3)

А 10. Прямая проходит через точки О(0;0) и В(2; -1). Тогда ее угловой коэффициент равен:

a ) ; b ) -2; c ) ; d ) 2

А 11. В координатной плоскости XOY линия задана уравнением х 2 — у 2 = 21
Тогда эта линия проходит через точки …

a ) (-2;5) и (5;2) b ) (7;5) и (5;2) c ) (5;2) и (11;-10) d ) (11;-10) и (-7; 5)

А 12. Установите соответствие между кривой второго порядка и ее уравнением у 2 =4х

a ) парабола b ) гипербола c ) эллипс d ) окружность

А 13. Величина действительной оси гиперболы равна:

a ) 9; b ) 12; c ) 6; d ) 8

А 14. Вычислить предел функции:

a ) 15; b ) 24; c ) 13; d ) – 4

А 15. Число точек разрыва функции равно

a ) 2 b ) 1 c ) 3 d ) 0

А 16. Производная функции у = sin 10 x имеет вид:

a) -10cos10x; b) 10cosx; c) 10cos10x; d) 10sinx;

А 17. Найти производную от функции, заданной параметрически:

a) e; b) e t ; c) -e 3t ; d) -2e 3t

А 18. Найти частную производную функции

a) 3x 2 ; b) 2y; c) 3x 2 + 2y; d) 3x 2 — 2y

А 19. Вычислить предел:

a ) 2 b ) -3 c ) 1 d ) 3

А 20. Определенный интеграл равен:

a ) 12; b ) ; c ) ; d ) 8

А 1. Если А и В=, то матрица С=2А-В имеет вид…

А2. Найти произведение матриц

А3. Если определитель второго порядка =1, то х= …

a ) -8 b ) -11 c ) 13 d ) -13

А 4. Определитель равен …

a ) 0 b ) 5 c ) 7 d ) 11

А 5. Решите систему

a ) (2; 4) b ) (-2; 4) c ) (1; 7) d ) (4; 2)

А 6. Система линейных уравнений имеет решение …

a ) x =3; у=2; z =0 b ) x =0; у=12; z =-2 c ) x =0; у=2; z =-1 d ) x =12; у=2; z =1

А 7. Для точек А(5;1) и В(-2;-6) уравнение прямой может быть записано в виде …

a ) у=-2х+11 b ) у=х-4 c ) у=0,5х-5 d ) у =-х/3+1

А 8. Укажите правильное соответствие между уравнением и типами уравнений прямой на плоскости

a ) уравнение прямой, параллельной оси абсцисс

b ) уравнение прямой с угловым коэффициентом

c ) уравнение прямой в отрезках

d ) общее уравнение прямой

А 9. Направляющий вектор прямой равен:

a ) (2; -5) b ) (-2; 5) c ) (-2; -5) d ) (3; 2).

А 10. Прямая проходит через точки О (0; 0) и С(-1; 2). Тогда ее угловой коэффициент равен:

А 11. В координатной плоскости XOY линия задана уравнением
Тогда эта линия проходит через точки …

a ) (4; -3) и (12; 5) b ) (12; 5) и (2; 5) c ) (2; 5) и (-1;1) d ) (-1; 1) и (4; -3)

А 12. Координаты центра окружности заданной уравнением равны:

a ) (2; -5) b ) (-2; 5) c ) (-2; -5) d ) (2; 5).

А 13. Величина большой полуоси эллипса х 2 +4у 2 =16 равна:

a ) 16; b ) 4; c ) 8; d ) 12.

А 14. Вычислить предел функции:

a ) 1 b ) 2 c ) d ) 0

А 15. Число точек разрыва функции равно…

a ) 2 b ) 1 c ) 3 d ) 0

А 16. Производная функции у = tg 5 x имеет вид

a ) ; b ) ; c ) 5 ctg 5 x ; d )

А 17. Найти производную от функции, заданной параметрически:

a ) t ; b ) 2 t +2; c ) -; d )

А 18. Найти частную производную функции

a) 3x 2 ; b) e y ; c) 3x 2 + e y ; d) 3x 2 — 2y

А 19. Вычислить предел:

a ) 0 b ) -3 c ) 1 d ) 3

А 20. Определенный интеграл равен:

a ) 4; b ) 12; c ) 8; d )

А 1. Если А и В=, то матрица С=3А-В имеет вид…

А 2. Найти произведение матриц

А3. Если определитель второго порядка =17, то х= …

a ) -3 b ) -37 c ) 3 d ) 37

А 4. Определитель равен …

a ) -18 b ) 0 c ) 2 d ) 14

А 5. Решите систему

a ) (2; 5) b ) (-2; 5) c ) (5; 2) d ) (4; 2)

А 6. Система линейных уравнений имеет решение …

a ) x =-3; у=2; z =0 b ) x =2; у=0; z =-3 c ) x =0; у=2; z =3 d ) x =1; у=2; z =-1

А 7. Для точек А(3; 2) и В(-2; -3) уравнением прямой является …

a ) х+у-1=0 b ) х+у+1=0 c ) х-у-1=0 d ) 5х-у-1=0

А 8. Укажите правильное соответствие между уравнением и типами уравнений прямой на плоскости х=6

a ) уравнение прямой с угловым коэффициентом

b ) уравнение прямой, параллельной оси ординат

c ) уравнение прямой в отрезках

d ) общее уравнение прямой

А 9. Нормальный вектор прямой равен:

a ) (-5;3) b ) (5;-3) c ) (5;3) d ) (-5;-3).

А 10. Прямая проходит через точки В(1;-2) и О(0;0). Тогда ее угловой коэффициент равен:

a ) ; b ) 2; c ) ; d ) -2

А 11. В координатной плоскости XOY линия задана уравнением 3у 2 = -х+6. Тогда эта линия проходит через точки …

a ) (-6; -2) и (3; 1) b ) (-3; -1) и (2; 5) c ) (-2; 5) и (-3; 21) d ) (3; 2) и (-3; 2)

А 12. Найдите соответствие между заданным уравнением и видами кривых второго порядка

a ) парабола b ) гипербола c ) эллипс d ) окружность

А13. Величина мнимой оси гиперболы 4 x 2 -25 y 2 =100 равна

a ) 25; b ) 10; c ) 4; d ) 8

А 14. Вычислить предел функции:

a ) 49 b ) 39 c ) 57 d ) 42

А 15. Число точек разрыва функции равно…

a ) 2 b ) 1 c ) 3 d ) 0

А 16. . Производная функции y =3 cos 6 x имеет вид:

a) -6sin6x b) -18cos6x c) _-3sin6x d) _-18sin6x

А 17. Найти производную от функции, заданной параметрически:

a ) 5; b ) 2 t ; c ) -; d )

А 18. Найти частную производную функции

a) 3x 2 ; b) e y ; c) 3x 2 + e y ; d) 3x 2 — 2y

А 19. Вычислить предел:

a ) 0 b ) 54 c ) 12 d ) 3

А 20. Определенный интеграл равен:

a ) ; b ) 19,2; c ) 48; d )

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 920 человек из 80 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 685 человек из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 309 человек из 69 регионов

Ищем педагогов в команду «Инфоурок»

Дистанционные курсы для педагогов

«Взбодрись! Нейрогимнастика для успешной учёбы и комфортной жизни»

Свидетельство и скидка на обучение каждому участнику

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 582 244 материала в базе

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

Другие материалы

• 20.11.2018
• 794
• 1

• 20.11.2018
• 1267
• 136

• 20.11.2018
• 428
• 7

• 20.11.2018
• 818
• 37

• 20.11.2018
• 335
• 0

• 20.11.2018
• 1430
• 8

• 20.11.2018
• 246
• 0

• 20.11.2018
• 387
• 0

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 20.11.2018 216
• DOCX 201.1 кбайт
• 1 скачивание
• Оцените материал:

Настоящий материал опубликован пользователем Ханнанова Эльвира Адунисовна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 6 лет и 7 месяцев
• Подписчики: 0
• Всего просмотров: 357
• Всего материалов: 1

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Минпросвещения упростит процедуру подачи документов в детский сад

Время чтения: 1 минута

Инфоурок стал резидентом Сколково

Время чтения: 2 минуты

В Ростовской и Воронежской областях организуют обучение эвакуированных из Донбасса детей

Время чтения: 1 минута

В Курганской области дистанционный режим для школьников продлили до конца февраля

Время чтения: 1 минута

В Ленобласти школьники 5-11-х классов вернутся к очному обучению с 21 февраля

Время чтения: 1 минута

Объявлен конкурс дизайн-проектов для школьных пространств

Время чтения: 2 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

В координатной плоскости xoy линия задана уравнением

Пример 16. Через точку M(2, 0, —3) провести плоскость, параллельную двум прямым:

Решение. Найдём вектор нормали N искомой плоскости. Он должен быть перпендикулярен направляющим векторам l1 и l2 данных прямых. Поэтому в качестве N можно взять векторное произведение:

Значит, уравнение плоскости имеет вид: x + 4y + 14z + D = 0.

Точка M должна лежать на плоскости. Поэтому 2 + 4 · 0 + 14(—3) + D = 0. Отсюда D = 40. Итак, уравнение плоскости найдено:

x + 4y + 14z + 40 = 0.

5.5. Прямые на плоскости

В этом разделе мы рассматриваем геометрические задачи на некоторой плоскости. Удобно считать, что рассматриваемая плоскость есть координатная плоскость XOY, задаваемая в пространстве уравнением z = 0. Тогда 3-я координата у точек и у векторов не пишется, так как она всегда равна 0. Поэтому положение точки будем задавать двумя числами: абсциссой и ординатой. Векторы определяются своими координатами в базисе i, j. Уравнение F(x,y) = 0 задаёт на плоскости некоторую линию.

Теорема 2. Любая прямая на плоскости может быть задана уравнением вида

Обратно, каждое уравнение такого вида (кроме случая A = B = 0) задаёт прямую. Вектор N = (A, B) перпендикулярен прямой (он называется вектором нормали этой прямой).

Доказательство. Считаем, что наша плоскость в пространстве задана уравнением z = 0. Тогда любая прямая на ней есть пересечение плоскости z = 0 и некоторой другой плоскости Ax + By + Cz + D = 0. Поэтому она задаётся системой уравнений . очевидно, равносильной одному уравнению Ax + By + D = 0.

Общее уравнение плоскости : описание, примеры, решение задач

В статье рассмотрим такой тип уравнений плоскости как общее уравнение, получим его вид и разберем на практических примерах. Рассмотрим частные случаи и понятие общего неполного уравнения плоскости.

Общее уравнение плоскости: основные сведения

Перед началом разбора темы вспомним, что такое уравнение плоскости в прямоугольной системе координат в трёхмерном пространстве. Пусть нам дана прямоугольная система координат O x y z в трехмерном пространстве, уравнением плоскости в заданной системе координат будет такое уравнение с тремя неизвестными x , y , и z , которому отвечали бы координаты всех точек этой плоскости и не отвечали бы координаты никаких прочих точек. Иначе говоря, подставив в уравнение плоскости координаты некоторой точки этой плоскости, получаем тождество. Если же в уравнение подставить координаты какой-то другой точки, не принадлежащей заданной плоскости, равенство станет неверным.

Также вспомним определение прямой, перпендикулярной к плоскости: прямая является перпендикулярной к заданной плоскости, если она перпендикулярна любой прямой, принадлежащей этой плоскости.

Любую плоскость, заданную в прямоугольной системе координат O x y z трехмерного пространства, можно определить уравнением A x + B y + C z + D = 0 . В свою очередь, любое уравнение A x + B y + C z + D = 0 определяет некоторую плоскость в данной прямоугольной системе координат трехмерного пространства. A , B , C , D – некоторые действительные числа, и числа A , B , C не равны одновременно нулю.

Теорема состоит из двух частей. Разберем доказательство каждой из них.

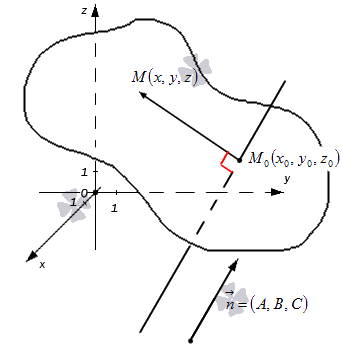
1. Первая часть теоремы гласит, что любую заданную плоскость возможно описать уравнением вида A x + B y + C z + D = 0 . Допустим, задана некоторая плоскость и точка M 0 ( x 0 , y 0 , z 0 ) , через которую эта плоскость проходит. Нормальным вектором этой плоскости является n → = ( A , B , C ) . Приведем доказательство, что указанную плоскость в прямоугольной системе координат O x y z задает уравнение A x + B y + C z + D = 0 .

Возьмем произвольную точку заданной плоскости M ( x , y , z ) .В таком случае векторы n → = ( A , B , C ) и M 0 M → = ( x — x 0 , y — y 0 , z — z 0 ) будут перпендикулярны друг другу, а значит их скалярное произведение равно нулю:

n → , M 0 M → = A x — x 0 + B ( y — y 0 ) + C ( z — z 0 ) = A x + B y + C z — ( A x 0 + B y 0 + C z 0 )

Примем D = — ( A x 0 + B y 0 + C z 0 ) , тогда уравнение преобразуется в следующий вид: A x + B y + C z + D = 0 . Оно и будет задавать исходную плоскость. Первая часть теоремы доказана.

1. Во второй части теоремы утверждается, что любое уравнение вида A x + B y + C z + D = 0 задает некоторую плоскость в прямоугольной системе координат O x y z трехмерного пространства. Докажем это.

В теореме также указано, что действительные числа А , B , C одновременно не являются равными нулю. Тогда существует некоторая точка M 0 ( x 0 , y 0 , z 0 ) , координаты которой отвечают уравнению A x + B y + C z + D = 0 , т.е. верным будет равенство A x 0 + B y 0 + C z 0 + D = 0 . Отнимем левую и правую части этого равенства от левой и правой частей уравнения A x + B y + C z + D = 0 . Получим уравнение вида

A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 , и оно эквивалентно уравнению A x + B y + C z + D = 0 . Докажем, что уравнение A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 задает некоторую плоскость.

Уравнение A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 являет собой условие, необходимое и достаточное для перпендикулярности векторов n → = ( A , B , C ) и M 0 M → = x — x 0 , y — y 0 , z — z 0 . Опираясь на утверждение, указанное перед теоремой, возможно утверждать, что при справедливом равенстве A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 множество точек M ( x , y , z ) задает плоскость, у которой нормальный вектор n → = ( A , B , C ) . При этом плоскость проходит через точку M ( x 0 , y 0 , z 0 ) . Иначе говоря, уравнение A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 задает в прямоугольной системе координат O x y z трехмерного пространства некоторую плоскость. Таким, образом, эквивалентное этому уравнению уравнение A x + B y + C z + D = 0 также определяет эту плоскость. Теорема доказана полностью.

Уравнение вида A x + B y + C z + D = 0 называют общим уравнением плоскости в прямоугольной системе координат O x y z трехмерного пространства.

Допустим, задано некоторое общее уравнение плоскости λ · A x + λ · B y + λ · C z + λ · D = 0 , где λ – некое действительное число, не равное нулю. Это уравнение также задает в прямоугольной системе координат некоторую плоскость, совпадающую с плоскостью, определяемую уравнением A x + B y + C z + D = 0 , поскольку описывает то же самое множество точек трехмерного пространства. Например, уравнения x — 2 · y + 3 · z — 7 = 0 и — 2 · x + 4 · y — 2 3 · z + 14 = 0 задают одну и ту же плоскость, поскольку им обоим отвечают координаты одних и тех же точек трехмерного пространства.

Раскроем чуть шире смысл теорем.

В пределах заданной системы координат плоскость и общее уравнение, ее определяющее, неразрывно связаны: каждой плоскости отвечает общее уравнение плоскости вида A x + B y + C z + D = 0 ( при конкретных значениях чисел A , B , C , D ). В свою очередь, этому уравнению отвечает заданная плоскость в заданной прямоугольной системе координат.

Укажем пример как иллюстрацию этих утверждений.

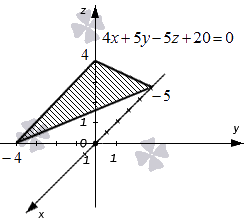
Ниже приведен чертеж, на котором изображена плоскость в фиксированной прямоугольной системе координат трехмерного пространства. Заданной плоскости отвечает общее уравнение вида 4 x + 5 y – 5 z + 20 = 0 , и ему соответствуют координаты любой точки этой плоскости. В свою очередь, уравнение 4 x + 5 y – 5 z + 20 = 0 описывает в заданной системе координат множество точек, которые составляют изображенную плоскость.

Общее уравнение плоскости, проходящей через точку

Повторимся: точка M 0 ( x 0 , y 0 , z 0 ) лежит на плоскости, заданной в прямоугольной системе координат трехмерного пространства уравнением A x + B y + C z + D = 0 в том случае, когда подставив координаты точки M 0 ( x 0 , y 0 , z 0 ) в уравнение A x + B y + C z + D = 0 , мы получим тождество.

Заданы точки M 0 ( 1 , — 1 , — 3 ) и N 0 ( 0 , 2 , — 8 ) и плоскость, определяемая уравнением 2 x + 3 y — z — 2 = 0 . Необходимо проверить, принадлежат ли заданные точки заданной плоскости.

Решение

Подставим координаты точки М 0 в исходной уравнение плоскости:

2 · 1 + 3 · ( — 1 ) — ( — 3 ) — 2 = 0 ⇔ 0 = 0

Мы видим, что получено верное равенство, значит точка M 0 ( 1 , — 1 , — 3 ) принадлежит заданной плоскости.

Аналогично проверим точку N 0 . Подставим ее координаты в исходное уравнение:

2 · 0 + 3 · 2 — ( — 8 ) — 2 = 0 ⇔ 12 = 0

Равенство неверно. Таким, образом, точка N 0 ( 0 , 2 , — 8 ) не принадлежит заданной плоскости.

Ответ: точка М 0 принадлежит заданной плоскости; точка N 0 – не принадлежит.

Приведенное выше доказательство теоремы об общем уравнении дает нам возможность использовать важный факт: вектор n → = ( A , B , C ) — нормальный вектор для плоскости, определяемой уравнением A x + B y + C z + D = 0 . Так, если нам известен вид общего уравнения, то возможно записать координаты нормального вектора заданной плоскости.

В прямоугольной системе координат задана плоскость 2 x + 3 y — z + 5 = 0 . Необходимо записать координаты всех нормальных векторов заданной плоскости.

Решение

Мы знаем, что заданные общим уравнением коэффициенты при переменных x , y , z служат координатами нормального вектора заданной плоскости. Тогда, нормальный вектор n → исходной плоскости имеет координаты 2 , 3 , — 1 . В свою очередь, множество нормальных векторов запишем так:

λ · n → = λ · 2 , λ · 3 , — λ , λ ∈ R , λ ≠ 0

Ответ: λ · 2 , λ · 3 , — λ , λ ∈ R , λ ≠ 0

Разберем обратную задачу, когда требуется составить уравнение плоскости по заданным координатам нормального вектора.

Очевидным фактом является то, что нормальный вектор n → = ( A , B , C ) является нормальным вектором бесконечного множества параллельных плоскостей. Поэтому для обозначения конкретной плоскости введем дополнительное условие: зададим некоторую точку M 0 ( x 0 , y 0 , z 0 ) , принадлежащую плоскости. Так, задавая в условии нормальный вектор и некоторую точку плоскости, мы ее зафиксировали.

Общее уравнение плоскости с нормальным вектором n → = ( A , B , C ) будет выглядеть так: A x + B y + C z + D = 0 . По условию задачи точка M 0 ( x 0 , y 0 , z 0 ) принадлежит заданной плоскости, т.е. ее координаты отвечают уравнению плоскости, а значит верно равенство: A x 0 + B y 0 + C z 0 + D = 0

Вычитая соответственно правые и левые части исходного уравнения и уравнения A x 0 + B y 0 + C z 0 + D = 0 , получим уравнение вида A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0 . Оно и будет уравнением плоскости, проходящей через точку M 0 ( x 0 , y 0 , z 0 ) и имеющей нормальный вектор n → = ( A , B , C ) .

Возможно получить это уравнение другим способом.

Очевидным фактом является то, что все точки М ( x , y , z ) трехмерного пространства задают данную плоскость тогда и только тогда, когда векторы n → = ( A , B , C ) и M 0 M → = ( x — x 0 , y — y 0 , z — z 0 ) перпендикулярны или, иначе говоря, когда скалярное произведение этих векторов равно нулю:

n → , M 0 M → = A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0

Задана точка М 0 ( — 1 , 2 , — 3 ) , через которую в прямоугольной системе координат проходит плоскость, а также задан нормальный вектор этой плоскости n → = ( 3 , 7 , — 5 ) . Необходимо записать уравнение заданной плоскости.

Решение

Рассмотрим два способа решения.

1. Исходные условия позволяют получить следующие данные:

x 0 = — 1 , y 0 = 2 , z 0 = — 3 , A = 3 , B = 7 , C = — 5

Подставим их в общее уравнение плоскости, проходящей через точку, т.е. в A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0

3 ( x — ( — 1 ) ) + 7 ( y — 2 ) — 5 ( z — ( — 3 ) ) = 0 ⇔ 3 x + 7 y — 5 z — 26 = 0

1. Допустим, М ( x , y , z ) – некоторая точки заданной плоскости. Определим координаты вектора M 0 M → по координатам точек начала и конца:

M 0 M → = ( x — x 0 , y — y 0 , z — z 0 ) = ( x + 1 , y — 2 , z + 3 )

Чтобы получить искомое общее уравнение плоскости, необходимо также воспользоваться необходимым и достаточным условием перпендикулярности векторов и тогда:

n → , M 0 M → = 0 ⇔ 3 ( x + 1 ) + 7 ( y — 2 ) — 5 ( z + 3 ) = 0 ⇔ ⇔ 3 x + 7 y — 5 z — 26 = 0

Ответ: 3 x + 7 y — 5 z — 26 = 0

Неполное общее уравнение плоскости

Выше мы говорили о том, что, когда все числа А , B , C , D отличны от нуля, общее уравнение плоскости A x + B y + C z + D = 0 называют полным. В ином случае общее уравнение плоскости является неполным.

Разберем все возможные варианты общих неполных уравнений в прямоугольной системе координат трехмерного пространства.

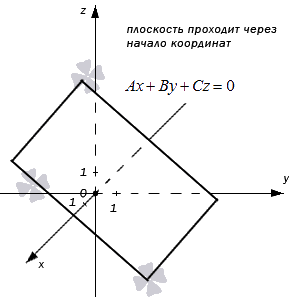
1. В случае, когда D = 0 , мы получаем общее неполное уравнение плоскости: A x + B y + C z + D = 0 ⇔ A x + B y + C z = 0

Такая плоскость в прямоугольной системе координат проходит через начало координат. В самом деле, если подставим в полученное неполное уравнение плоскости координаты точки О ( 0 , 0 , 0 ) , то придем к тождеству:

A · 0 + B · 0 + C · 0 = 0 ⇔ 0 ≡ 0

1. Если А = 0 , В ≠ 0 , С ≠ 0 , или А ≠ 0 , В = 0 , С ≠ 0 , или А ≠ 0 , В ≠ 0 , С = 0 , то общие уравнения плоскостей имеют вид соответственно: B y + C z + D = 0 , или A x + C z + D = 0 , или A x + B y + D = 0 . Такие плоскости параллельны координатным осям О x , O y , O z соответственно. Когда D = 0 , плоскости проходят через эти координатные оси соответственно. Также заметим, что неполные общие уравнения плоскостей B y + C z + D = 0 , A x + C z + D = 0 и A x + B y + D = 0 задают плоскости, которые перпендикулярны плоскостям O y z , O x z , O z y соответственно.

1. При А = 0 , В = 0 , С ≠ 0 , или А = 0 , В ≠ 0 , С = 0 , или А ≠ 0 , В = 0 , С = 0 получим общие неполные уравнения плоскостей: C z + D = 0 ⇔ z + D C = 0 ⇔ z = — D C ⇔ z = λ , λ ∈ R или B y + D = 0 ⇔ y + D B = 0 ⇔ y = — D B ⇔ y = λ , λ ∈ R или A x + D = 0 ⇔ x + D A = 0 ⇔ x = — D A ⇔ x = λ , λ ∈ R соответственно.

Эти уравнения определяют плоскости, которые параллельны координатным плоскостям O x y , O x z , O y z соответственно и проходят через точки 0 , 0 , — D C , 0 , — D B , 0 и — D A , 0 , 0 соответственно. При D = 0 уравнения самих координатных плоскостей O x y , O x z , O y z выглядят так: z = 0 , y = 0 , x = 0

Задана плоскость, параллельная координатной плоскости O y z и проходящая через точку М 0 ( 7 , — 2 , 3 ) . Необходимо составить общее уравнение заданной плоскости.

Р​​ешение

У​​​​​словием задачи определено, что заданная плоскость параллельна координатной плоскости O y z , а, следовательно, может быть задана общим неполным уравнением плоскости A x + D = 0 , A ≠ 0 ⇔ x + D A = 0 . Поскольку точка M 0 ( 7 , — 2 , 3 ) лежит на плоскости по условию задачи, то очевидно, что координаты этой точки должны отвечать уравнению плоскости x + D A = 0 , иначе говоря, должно быть верным равенство 7 + D A = 0 . Преобразуем: D A = — 7 , тогда требуемое уравнение имеет вид: x — 7 = 0 .

Задачу возможно решить еще одним способом.

Вновь обратим внимание на заданную условием задачи параллельность данной плоскости координатной плоскости O y z . Из этого условия понятно, что возможно в качестве нормального вектора заданной плоскости использовать нормальный вектор плоскости O y z : i → = ( 1 , 0 , 0 ) . Так, нам известны и точка, принадлежащая плоскости (задана условием задачи) и ее нормальный вектор. Таким образом, становится возможно записать общее уравнение заданной плоскости:

A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0 ⇔ ⇔ 1 · ( x — 7 ) + 0 · ( y + 2 ) + 0 · ( z — 3 ) = 0 ⇔ ⇔ x — 7 = 0

Ответ: x — 7 = 0

Задана плоскость, перпендикулярная плоскости O x y и проходящая через начало координат и точку М 0 ( — 3 , 1 , 2 ) .

Решение

Плоскость, которая перпендикулярна координатной плоскости O x y определяется общим неполным уравнением плоскости A x + B y + D = 0 ( А ≠ 0 , В ≠ 0 ) . Условием задачи дано, что плоскость проходит через начало координат, тогда D = 0 и уравнение плоскости принимает вид A x + B y = 0 ⇔ x + B A y = 0 .

Найдем значение B A . В исходных данных фигурирует точка М 0 ( — 3 , 1 , 2 ) , координаты которой должны отвечать уравнению плоскости. Подставим координаты, получим верное равенство: — 3 + B A · 1 = 0 , откуда определяем B A = 3 .

Так, мы имеем все данные, чтобы записать требуемое общее уравнение плоскости: x + 3 y = 0 .