В парабола уравнение директрисы y 1

Директриса параболы

Вы будете перенаправлены на Автор24

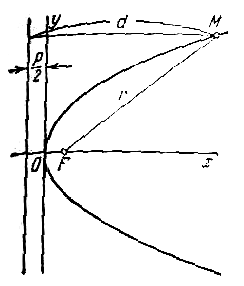
Директрисой параболы называют такую прямую, кратчайшее расстояние от которой до любой точки $M$, принадлежащей параболе точно такое же, как и расстояние от этой же точки до фокуса параболы $F$.

Рисунок 1. Фокус и директриса параболы

Основные понятия параболы

Отношение расстояний от точки $M$, лежащей на параболе, до этой прямой и от этой же точки до фокуса $F$ параболы называют эксцентриситетом параболы $ε$.

Чтобы найти эксцентриситет параболы, достаточно воспользоваться следующей формулой из определения эксцентриситета: $ε =\frac$, где точка $M_d$ — точка пересечения перпендикуляра, опущенного из точки $M$ c прямой $d$.

Каноническая парабола задается уравнением вида $y^2 = px$, где $p$ обязательно должно быть больше нуля.

Более часто приходится иметь дело с параболой, вершина которой не находится в точке начала координатных осей, и тогда уравнение параболы приобретает следующий вид:

$y = ax^2 + bx + c$, при этом коэффициент $a$ не равен нулю.

Чтобы найти директрису такой параболы, необходимо от такой формы перейти к канонической, ниже в примерах показано, как это сделать.

Расстояние от фокуса до директрисы параболы называется её фокальным параметром $p$. Уравнение директрисы канонической параболы имеет следующий вид: $x=-p/2$

Алгоритм составления уравнения директрисы параболы, заданной не каноническим уравнением

Готовые работы на аналогичную тему

Чтобы составить уравнение директрисы параболы, вершина которой не находится на пересечении осей координат, достаточно воспользоваться следующим алгоритмом:

1. Перенесите все слагаемые с $y$ в левую часть уравнения, а с $x$ — в правую.
2. Упростите полученное выражение.
3. Введите дополнительные переменные чтобы прийти к каноническому виду уравнения.

Составьте уравнение директрисы параболы, описанной уравнением $4x^2 + 24 x – 4y + 36 = 0$

Переносим все слагаемые с $y$ в левую часть и избавляемся от множителя, получаем:

$y^2 = x^2 + 6x – y + 9$

Приводим в форму квадрата:

Вводим дополнительные переменные $t = x + 3$ и $y = z$

В парабола уравнение директрисы y 1

Глава 20. Парабола

Параболой называется геометрическое место точек, для каждой из которых расстояние до некоторой фиксированной точки плоскости, называемой фокусом, равно расстоянию до некоторой фиксированной прямой, называемой директрисой. Фокус параболы обозначается буквой F , расстояние от фокуса до директрисы — буквой р. Число р называется параметром параболы.

Пусть дана некоторая парабола. Введем декартову прямоугольную систему координат так, чтобы ось абсцисс проходила через фокус данной параболы перпендикулярно к директрисе и была направлена от директрисы к фокусу; начало координат расположим посередине между фокусом и директрисой (рис.). В этой системе координат данная парабола будет определяться уравнением

(1)

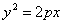
Уравнение (1) называется каноническим уравнением параболы. В этой же системе координат директриса данной параболы имеет уравнение

.

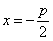
Фокальный радиус произвольной точки М( x; y ) параболы (то есть длина отрезка F(M ) может быть вычислен по формуле

.

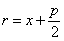
Парабола имеет одну ось симметрии, называемую осью параболы, с которой она пересекается в единственной точке. Точка пересечения параболы с осью называется ее вершиной. При указанном выше выборе координатной системы ось параолы совмещена с осью абсцисс, вершина находится в начале координат, вся парабола лежит в правой полуплоскости.

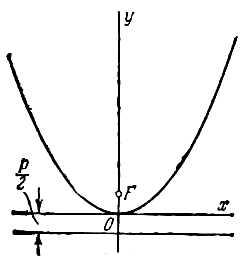
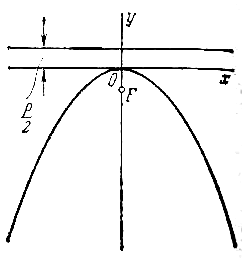
Если координатная система выбрана так, что ось абсцисс совмещена с осью параболы, начало координат — с вершиной, но парабола лежит в левой полуплоскости (рис.), то ее уравнение будет иметь вид

(2)

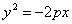
В случае, когда начало координат находится в вершине, а с осью совмещена ось ординат, парабола будет иметь уравнение

(3)

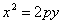
если она лежит в верхней полуплоскости (рис.), и

(4)

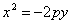
если в нижней полуплоскости (рис.)

Каждое из уравнений параболы (2), (3), (4), как и уравнение (1), называется каноническим.

Парабола: формулы, примеры решения задач

Определение параболы. Параболой называется множество всех точек плоскости, таких, каждая из которых находится на одинаковом расстоянии от точки, называемой фокусом, и от прямой, называемой директрисой и не проходящей через фокус.

Каноническое уравнение параболы имеет вид:

,

где число p, называемое параметром параболы, есть расстояние от фокуса до директрисы.

На чертеже линия параболы — бордового цвета, директриса — ярко-красного цвета, расстояния от точки до фокуса и директрисы — оранжевого.

В математическом анализе принята другая запись уравнения параболы:

то есть ось параболы выбрана за ось координат. Можно заметить, что ax² — это квадратный трёхчлен ax² + bx + c , в котором b = 0 и c = 0 . График любого квадратного трёхчлена, то есть левой части квадратного уравнения, будет параболой.

Фокус параболы имеет координаты

Директриса параболы определяется уравнением .

Расстояние r от любой точки параболы до фокуса определяется формулой .

Для каждой из точек параболы расстояние до фокуса равно расстоянию до директрисы.

Пример 1. Определить координаты фокуса параболы

Решение. Число p расстояние от фокуса параболы до её директрисы. Начало координат в данном случае — в роли любой точки, расстояния от которой от фокуса до директрисы равны. Находим p:

Находим координаты фокуса параболы:

Пример 2. Составить уравнение директрисы параболы

Решение. Находим p:

Получаем уравнение директрисы параболы:

Пример 3. Составить уравнение параболы, если расстояние от фокуса до директрисы равно 2.

Решение. Параметр p — это и есть данное расстояние от фокуса до директрисы. Подставляем и получаем:

Траектория камня, брошенного под углом к горизонту, летящего футбольного мяча или артиллерийского снаряда будет параболой (при отсутствии сопротивления воздуха). Зона достижимости для пущенных камней вновь будет параболой. В данном случае речь идёт об огибающей кривой траекторий камней, выпущенных из данной точки под разными углами, но с одной и той же начальной скоростью.

Парабола обладает следующим оптическим свойством: все лучи, исходящие из источника света, находящегося в фокусе параболы, после отражения оказываются направленными параллельно её оси. Это свойство параболы используется при изготовлении прожекторов, автомобильных фар, карманных фонариков, зеркала которых имеют вид параболоидов вращения (фигур, получающихся при вращении параболы вокруг оси). Пучок параллельных лучей, двигающийся вдоль оси параболы, отражаясь, собирается в её фокусе.