Окружность в полярных координатах
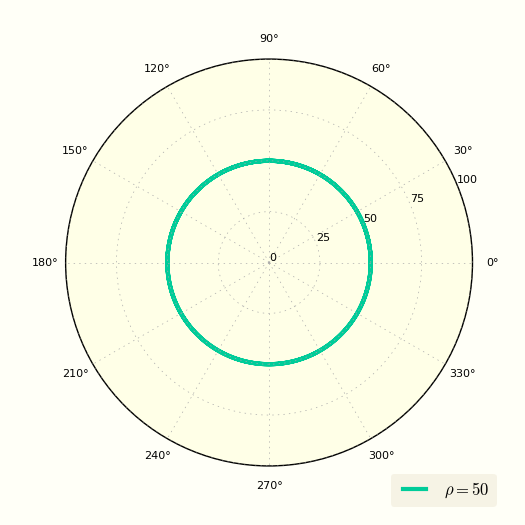
Уравнение окружности в полярных координатах выглядит очень просто
Это уравнение показывает, что ρ вообще не зависит от угла φ.
Построение окружности по простому уравнению в полярной системе координат
Еще одно уравнение окружности в полярных координатах
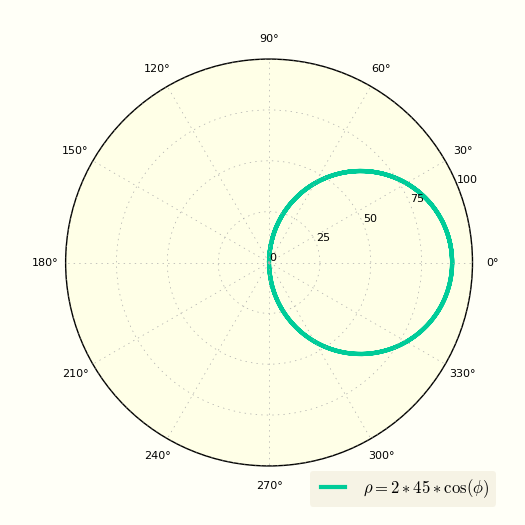
Первый пример был очень простым, теперь возьмем окружность смещенную по оси X в декартовых координатах и получим ее полярное уравнение.
Известно, что окружность в декартовой прямоугольной системе координат описывается уравнением:
Используя эти формулы и подставив их в (1) мы получим:
Уравнение окружности в полярных координатах
Изначально после подстановки имеем
И этого уравнения получается система
Первое уравнение системы описывает полюс окружности.
Второе описывает саму окружность в полярной системе координат.
В итоге получаем:
Построение окружности в полярной системе координат
Теперь сместим окружность по вверх, очередное уравнение окружности в полярных координатах
В данном варианте мы сместим окружность по оси Y в декартовых координатах и получим ее полярное уравнение.
При таком смещении окружность описывается уравнением:
И этого уравнения получается система
Первое уравнение системы описывает полюс окружности.
Второе описывает саму окружность в полярной системе координат.
Уравнение окружности в полярной системе координат.
Определим уравнение окружности, проходящей через полюс системы координат, центр которой C расположен на полярной оси, а радиус равен R. Выполним построения:
Далее отметим на окружности любую точку А и В, причем точка В — конец диаметра. Соединим выбранную пару точек. Угол ОАВ — прямой, а потому, так как диаметр равен 2R, из прямоугольного треугольника АОВ имеем:
Если же центр является началом координат, то уравнение принимает вид:
Так же уравнение может принимать вид:
Для ситуации, когда центр окружности расположен на прямой перпендикулярной полярной оси и проходящей через полюс:
Полярная система координат
Для определения положения точки на плоскости можно пользоваться и другими системами координат. В частности широко используется полярная система координат. На плоскости выберем точку и обозначим ее О. Рассмотрим луч с началом в О, а на луче выберем единичный отрезок ОЕ. Точка О называется полюсом, а луч ОЕ называется полярной осью. Положение любой точки М на плоскости, отличной от О определяется парой чисел: расстоянием r = |OM| и величиной угла между лучами ОЕ и ОМ, причем угол ориентирован, т. е. положительное направление против часовой стрелки, а отрицательное – по часовой стрелке. Для точки О считаем r = 0, а угол j не определен.
Для рассматриваемых полярных координат мы имеем r ³ 0, а j Î R. Однако, в нашем случае пары чисел (r, j) и (r, j + 2 
Например, пара чисел (−3; 

Пример 1. Найдем уравнение прямой, не проходящей через полюс О. Зададим эту прямую числом р, длиной отрезка ОР и углом a, где Р – основание перпендикуляра ОР на прямую, а a –ориентированный угол между лучом ОР и полярной осью.
Если произвольная точка М(r, j) принадлежит данной прямой, то р = rcos (j −a) и обратно.
Поэтому имеем уравнение прямой: 
Пример 2. Луч 
Решение. Примем за полярную систему координат начальное положение луча 






Рассмотрим согласованную с полярной системой координат прямоугольную декартовую систему. Известна связь между координатами этих систем.

Заменяя полярные координаты, получим параметрические уравнения траектории точки М:
РЕШЕНИЕ НУЛЕВОГО ВАРИАНТА
КОНТРОЛЬНОЙ РАБОТЫ
1.Найти уравнение плоскости, проходящей через прямую
перпендикулярно плоскости: 3х – 5 у + 5 z + 3 = 0.
Решение. Искомая плоскость a будет проходить через данную прямую, а следовательно через точку прямой М0 (2; – 3; – 1). Направляющий вектор 




Разложим определитель по первой строке


a: 
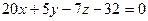
Ответ: 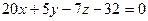
2.Даны плоскости, заданные в О 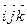
a: 2х – 3у + 3 = 0, b: х – у + z +2 = 0.
Найти уравнение плоскости, проходящей через линию пересечения данных плоскостей и перпендикулярную плоскости b.
Решение. Найдем две общие точки данных плоскостей. Для этого решим систему уравнений:
Пусть у = 0, тогда система примет вид
Отсюда получим, что х = 

Решением системы будет тройка чисел 


Отсюда получим, что х = 0, z = 



Из уравнения плоскости b находим ее нормальный вектор 
Для составления уравнения искомой плоскости обратим внимание на то, что точки М1 и М2 принадлежат ей, а вектор 

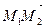








3.Найти каноническое уравнение прямой, проходящей через точку А(6; 2; 3) перпендикулярно плоскости, проходящей через точки В (1; 4; 4), С (0; 2; 4), D (1; 3; 3).
Решение. Найдем уравнение плоскости (BCD) по трем точкам B, C, D


Разложив определитель по первой строке, получим уравнение плоскости (BCD):

Нормальный вектор 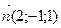
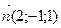


Ответ: 
4. Даны прямые, заданные в О 
ℓ1: 

Найти уравнение плоскости, проходящей через первую прямую параллельно второй прямой.
Решение. Согласно условию задачи точка М0 (– 1; – 1; 4), принадлежащая первой прямой, лежит в искомой плоскости. Кроме этого имеем два вектора: 

a: 
Раскрываем определитель по первой строке:
= – 3(х + 1) + 6(у +1) – 12(z – 4) = – 3х + 6у – 12z +51.
Следовательно, – 3х + 6у – 12z +51 = 0 и получаем уравнение плоскости a: х –2у + 4z – 17 = 0.
5. Вычислить расстояние от точки P (-1; 1; -2) до плоскости, проходящей через точки, заданные в О 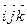
Решение. Найдем уравнение плоскости (АВС) по трем заданным точкам:

Разложив определитель по первой строке, получим:

Следовательно, 
Воспользуемся известной формулой для вычисления расстояния от точки до плоскости

Ответ: 
Тест
Отметьте номер правильного ответа в бланке ответов
| Задания | Варианты ответов | |
| А1 | Написать уравнение прямой, проходящей через две заданные точки М1(1; – 2; 1) и М2(3; 1; – 1) | 1)  2) 2)  3) 3)  4) 4)  5) 5)  =0 =0 |
| A2 | Найти расстояние от точки М0 (–1; 2) до прямой ℓ:  | 1)  2) 2)  3) 2 4) 5 5) 3) 2 4) 5 5)  |
| A3 | Найти расстояние между прямыми ℓ1: 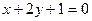 и ℓ2: и ℓ2:  | 1) 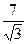 2) 5 3) 2) 5 3)  4) 4)  5) 6 5) 6 |
| А4 | Найти косинус угла между прямыми ℓ1 и ℓ2, если ℓ1 :  и ℓ2: и ℓ2:  | 1)  2) 2)  3) 3)  4) 4)  5) 0 5) 0 |
| А5 | Найти уравнение касательной к окружности  в точке в точке  | 1)  2) 2)  3) 3)  4) 4)  5) 5)  |
| А6 | Две стороны квадрата лежат на прямых ℓ1 :  и ℓ2: и ℓ2:  . Вычислить его площадь . Вычислить его площадь | 1) 64 2) 81 3) 16 4) 49 5) 25 |
| А7 | В О  заданы точки: А(1; 0), В(0; 1), С(1; 2) Найти общее уравнение прямой (ВС). заданы точки: А(1; 0), В(0; 1), С(1; 2) Найти общее уравнение прямой (ВС). | 1)  2) х + у – 1=0 3) у = х +1 4) 2) х + у – 1=0 3) у = х +1 4)  5) х – у + 1=0 5) х – у + 1=0 |
| А8 | В О  заданы точки: А(1; 0), В(0; 1), С(1; 2) Найти общее уравнение медианы (АМ) треугольника АВС. заданы точки: А(1; 0), В(0; 1), С(1; 2) Найти общее уравнение медианы (АМ) треугольника АВС. | 1)  2)х– у+1=0 3)х+3у –3=0 4) 3х+у – 3=0, 5) 2)х– у+1=0 3)х+3у –3=0 4) 3х+у – 3=0, 5)  |
| А9 | В О  заданы точки: А(1; 1), В(0; 2), С(2; 4) Найти общее уравнение биссектрисы угла ÐАВС. заданы точки: А(1; 1), В(0; 2), С(2; 4) Найти общее уравнение биссектрисы угла ÐАВС. | 1) х – у = 0, 2) 2х+3у – 1 =0, 3) х = 2, 4) у – 2 = 0, 5) у = 2х. |
| А10 | В О  заданы точки: А(1; 1),В(0; 2), С(2; 4). Вычислить расстояние от точки А до биссектрисы угла В в треугольнике АВС. заданы точки: А(1; 1),В(0; 2), С(2; 4). Вычислить расстояние от точки А до биссектрисы угла В в треугольнике АВС. | 1) 1, 2) -2, 3) 4, 4) 0, 5) 2. |
| А11 | В О  заданы точки:А(1; 1), В(0; 2), С(2; 4). Вычислить площадь треугольника АВВ1 , где ВВ1 — биссектриса угла В в треугольнике АВС. заданы точки:А(1; 1), В(0; 2), С(2; 4). Вычислить площадь треугольника АВВ1 , где ВВ1 — биссектриса угла В в треугольнике АВС. | 1) 2, 2) 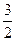 , 3) , 3)  , 4) -1, 5) 3 , 4) -1, 5) 3 |
| А12 | В О 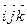 заданы плоскости a:х-у+z = -3, b: 2x-3z+4=0 найти уравнение плоскости, проходящей через линию пересечения данных плоскостей и ^ a. заданы плоскости a:х-у+z = -3, b: 2x-3z+4=0 найти уравнение плоскости, проходящей через линию пересечения данных плоскостей и ^ a. | 1)х – у — 8z=19; 2)21x — 3y — 24z+19=0; 3)x — 3y+5z — 21=0; 4) x+3y — 5z — 21=0; 5) 21x — 3y+24z+19=0 |
| A13 | Уравнение прямой имеет вид, если она проходит через точку В(4,2,-3) и перпендикулярна плоскости ACD, где A(1,-1,1), C(0,2,4), D(1,3,3), (O 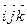 ). ). | 1)21x-3y+24z+19=0;2)  3) 3)  ; 4)х – у – z +3=0; 5) ; 4)х – у – z +3=0; 5)  |
| А14 | Уравнение плоскости ACD имеет вид, где A(1,-1,1),C(0,2,4), D(1,3,3), (O 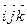 ). ). | 1) 3х – у + 2z – 6 =0, 2) 3х + у + 2z + 6 =0, 3) у + 2z – 6 =0, 4) 3х + 2z – 6 =0, 5) 3х – у -2z – 6 =0 |
| A15 | Найти расстояние от точки B(4,2,-3) до плоскости ACD, где A(1,-1,1),C(0,2,4), D(1,3,3), (O 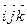 ). ). | 1) 2, 2)  , 3) 3, 4) , 3) 3, 4)  , 5) , 5)  |
| А1 | А2 | А3 | А4 | А5 | А6 | А7 | А8 | А9 | А10 | А11 | А12 | А13 | А14 | А15 |
Список литературы
1. А.Д. Александров, Н.Ю. Нецветаев. Геометрия. — М.: Наука, 1990.
2. Л.С. Атанасян, В.Т. Базылев. Геометрия. Ч. 1. — М.: Просвещение, 1986.
3. В.Т. Базылев, К.И. Дуничев и др. Геометрия. — Ч. 1. — М.: Просвещение, 1974.
4. В.Т. Базылев, К.И. Дуничев и др. Под ред. В.Т. Базылева. Сборник задач по геометрии. — М.: Просвещение, 1980.
5. Беклемишева Л.А. и др. Сборник задач по аналитической геометрии: Уч.пособие. –М. 2003.
6. Бортаковский А.С., Пантелеев А.В. Аналитическая геометрия в примерах и задачах: Учебное пособие. –М.: Высшая школа, 2005.
7. А.Л. Вернер, Б.Е. Кантор, С.А. Франгулов. Геометрия, ч.1.- С. Петербург, 1997.
8. Л.С. Атанасян, В.А. Атанасян. Сборник задач по геометрии. Ч. 1. — М.: Просвещение, 1973.
9. Ефимов Н.В., Розендорн Э.Р. Линейная алгебра и многомерная геометрия. –М., 2004. –464 с.
10. Ефимов Н.В. Высшая геометрия: Учебник для вузов. –.М.: Физматлит, 2003. –584 с.
11. Жаферов А.Ф. Геометрия: в 2-х частях. Ч.1. –Новосибирск: Сиб.унив.изд-во, 2002. –271 с.
12. Жаферов А.Ф. Геометрия: в 2-х частях. Ч.2. –Новосибирск: Сиб.унив.изд-во, 2003. –267 с.
13. Кострикин А.И., Манин Ю.И. Линейная алгебра и геометрия. –М.: МГУ, 1980. –320 с.
14. Д.В. Клетеник. Сборник задач по аналитической геометрии. — М.: Наука, 1964.
15. А.В. Погорелов. Геометрия. — М.: Наука, 1984.
16. О.Н. Цубербиллер. Сборник задач по аналитической геометрии. — М.: Наука, 1966.
Виктор Анатольевич Долженков
Елена Георгиевна Соловьева
Игорь Викторович Горчинский
Лицензия ИД № 06248 от 12.11.2001 г.
Подписано в печать Формат 60х84/16. Печать офсетная.
http://www.calc.ru/Uravneniye-Okruzhnosti-V-Polyarnoy-Sisteme-Koordinat.html
http://megalektsii.ru/s56098t7.html