Лекция. Метод наименьших квадратов (мнк) Оценка параметров линейных уравнений регрессии
| Название | Метод наименьших квадратов (мнк) Оценка параметров линейных уравнений регрессии |
| Анкор | Лекция |
| Дата | 30.06.2021 |
| Размер | 69 Kb. |
| Формат файла |  |
| Имя файла | 082_Lektsiya24_MNK.doc |
| Тип | Документы #222536 |
 С этим файлом связано 1 файл(ов). Среди них: Основые формы самостоятельных занятий.pdf. С этим файлом связано 1 файл(ов). Среди них: Основые формы самостоятельных занятий.pdf.  Показать все связанные файлы Подборка по базе: Теория и методика занятий волейболом.docx, Алгоритм для реш нер-в методом интервалов.docx, 1.История и методология науки.pdf, тема ПС и ЭПС методматериал.docx, реферат Теория и методика физической культуры.docx, Коронавирусная инфекция и методы её профилактики.docx, Отчет по лабораторной работе №1 исследование электростатического, Игра как метод обучения.docx, Тест 2 Методика преподавания по программам дополнительного образ, Классификации методов психологии.docx Показать все связанные файлы Подборка по базе: Теория и методика занятий волейболом.docx, Алгоритм для реш нер-в методом интервалов.docx, 1.История и методология науки.pdf, тема ПС и ЭПС методматериал.docx, реферат Теория и методика физической культуры.docx, Коронавирусная инфекция и методы её профилактики.docx, Отчет по лабораторной работе №1 исследование электростатического, Игра как метод обучения.docx, Тест 2 Методика преподавания по программам дополнительного образ, Классификации методов психологии.docxМетод наименьших квадратов (МНК)Оценка параметров линейных уравнений регрессииПроцедура построения системы нормальных уравнений и исходное соотношение, используемое в МНК. Для определения параметров функции, используемой в эконометрической модели, разработаны различные методы, наиболее простым и известным из которых является метод наименьших квадратов (МНК). Рассмотрим суть этого метода на примере парной линейной регрессии. Применение МНК к парной линейной регрессии . Итак, необходимо определить параметры а и b для функции Чтобы построенная модель была как можно ближе к реальности, эта сумма должна быть как можно меньше. Отметим, что полученная сумма представляет собой функцию от двух переменных а и b, и чтобы найти ее минимум, приравняем к нулю ее частные производные по а и по b: Итак, получено два линейных уравнения с двумя неизвестными – а и b (система линейна относительно параметров регрессии). Такую систему называют системой нормальных уравнений. Решив ее, можно определить искомые параметры. где 1) методом Гаусса, который заключается в том, что матрицу коэффициентов в уравнениях поэтапно преобразуют в единичную матрицу путем линейных преобразований этих уравнений (разрешающее уравнение делят на разрешающий элемент, получая на его месте единицу, а из всех остальных уравнений вычитают преобразованное разрешающее, умноженное на те коэффициенты, которые стоят в этих уравнениях в разрешающем столбце, с целью получить на их месте нули); 2) методом Крамера, который заключается в том, что рассчитывают определитель матрицы коэффициентов в уравнениях, а затем рассчитывают частные определители, поочередно заменяя один из столбцов в этой матрице столбцом свободных членов; значения переменных равны отношениям соответствующих частных определителей к определителю первой матрицы; 3) методом обратной матрицы и т.д. Матричная форма МНКРассмотрим систему нормальных уравнений МНК, используя обозначения матричной алгебры. А именно, введем следующие обозначения: где m – число признаков-факторов, n — число наблюдений. Каждая строка матрицы соответствует одному из наблюдений, а каждый столбец, кроме первого, — одному из факторов. Если транспонировать матрицу X размерности n x (m + 1), в полученной матрице X Т размерности (m + 1) x n каждый столбец будет соответствовать одному из факторов, а строки — наблюдениям. Перемножив полученную матрицу X Т на X, получим симметричную матрицу размерности (m + 1) x (m + 1): Тогда система уравнений примет вид X Т XА = X Т Y. Умножим слева обе части этого выражения на матрицу (X Т X) -1 , получим: А = (X Т X) -1 X Т Y 2. Для нахождения параметров линейной регрессии минимизируют сумму квадратов отклонений фактических значений результата от подсчитанных по уравнению регрессии. Метод, в основе которого лежит эта идея, — метод … (напишите два слова в родительном падеже) 5. В модель множественной регрессии включено семь факторов. Сколько уравнений будет в системе нормальных уравнений? 7. В модель множественной регрессии включено три фактора. Сколько уравнений будет в системе нормальных уравнений? Система нормальных уравнений и явный вид ее решения при оценивании методом наименьших квадратов линейной модели парной регрессииПредположим, что в ходе регрессионного анализа была установлена линейная взаимосвязь между исследуемыми переменными х и у, которая описывается моделью регрессии вида: В результате оценивания данной эконометрической модели определяются оценки неизвестных коэффициентов. Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК). Метод наименьших квадратов позволяет получить такие оценки параметров β0и β1, при которых сумма квадратов отклонений фактических значений результативного признака y от расчетных (теоретических) y˜ минимальна: В процессе минимизации функции (1) неизвестными являются только значения коэффициентов β0 и β1, потому что значения результативной и факторной переменных известны из наблюдений. Для определения минимума функции двух переменных вычисляются частные производные этой функции по каждому из оцениваемых параметров и приравниваются к нулю. Результатом данной процедуры будет стационарная система уравнений для функции (2):
Если разделить обе части каждого уравнения системы на (-2), раскрыть скобки и привести подобные члены, то получим систему нормальных уравнений для функции регрессии вида yi=β0+β1xi: Если решить данную систему нормальных уравнений, то мы получим искомые оценки неизвестных коэффициентов модели регрессии β0 и β1: y – среднее значение зависимой переменной; x – среднее значение независимой переменной; xy – среднее арифметическое значение произведения зависимой и независимой переменных; G 2 (x) – дисперсия независимой переменной; Gcov (x, y) – ковариация между зависимой и независимой переменными. Таким образом, явный вид решения системы нормальных уравнений может быть записан следующим образом: Метод наименьших квадратов.Поможем написать любую работу на аналогичную тему Сущность метода наименьших квадратов заключается в отыскании параметров модели тренда, которая лучше всего описывает тенденцию развития какого-либо случайного явления во времени или в пространстве (тренд – это линия, которая и характеризует тенденцию этого развития). Задача метода наименьших квадратов (МНК) сводится к нахождению не просто какой-то модели тренда, а к нахождению лучшей или оптимальной модели. Эта модель будет оптимальной, если сумма квадратических отклонений между наблюдаемыми фактическими величинами и соответствующими им расчетными величинами тренда будет минимальной (наименьшей): где и соответствующей ей расчетной величиной тренда, МНК самостоятельно применяется довольно редко. Как правило, чаще всего его используют лишь в качестве необходимого технического приема при корреляционных исследованиях. Следует помнить, что информационной основой МНК может быть только достоверный статистический ряд, причем число наблюдений не должно быть меньше 4-х, иначе, сглаживающие процедуры МНК могут потерять здравый смысл. Инструментарий МНК сводится к следующим процедурам: Первая процедура. Выясняется, существует ли вообще какая-либо тенденция изменения результативного признака при изменении выбранного фактора-аргумента, или другими словами, есть ли связь между «у» и «х». Вторая процедура. Определяется, какая линия (траектория) способна лучше всего описать или охарактеризовать эту тенденцию. Третья процедура. Рассчитываются параметры регрессионного уравнения, характеризующего данную линию, или другими словами, определяется аналитическая формула, описывающая лучшую модель тренда. Пример. Допустим, мы имеем информацию о средней урожайности подсолнечника по исследуемому хозяйству (табл. 9.1). Поскольку уровень технологии при производстве подсолнечника в нашей стране за последние 10 лет практически не изменился, значит, по всей видимости, колебания урожайности в анализируемый период очень сильно зависели от колебания погодно-климатических условий. Действительно ли это так? Первая процедура МНК. Проверяется гипотеза о существовании тенденции изменения урожайности подсолнечника в зависимости от изменения погодно-климатических условий за анализируемые 10 лет. В данном примере за «y» целесообразно принять урожайность подсолнечника, а за «x» – номер наблюдаемого года в анализируемом периоде. Проверку гипотезы о существовании какой-либо взаимосвязи между «x» и «y» можно выполнить двумя способами: вручную и при помощи компьютерных программ. Конечно, при наличии компьютерной техники данная проблема решается сама собой. Но, чтобы лучше понять инструментарий МНК целесообразно выполнить проверку гипотезы о существовании связи между «x» и «y» вручную, когда под рукой находятся только ручка и обыкновенный калькулятор. В таких случаях гипотезу о существовании тенденции лучше всего проверить визуальным способом по расположению графического изображения анализируемого ряда динамики — корреляционного поля: Корреляционное поле в нашем примере расположено вокруг медленно возрастающей линии. Это уже само по себе говорит о существовании определенной тенденции в изменении урожайности подсолнечника. Нельзя говорить о наличии какой-либо тенденции лишь тогда, когда корреляционное поле похоже на круг, окружность, строго вертикальное или строго горизонтальное облако, или же состоит из хаотично разбросанных точек. Во всех остальных случаях следует подтвердить гипотезу о существовании взаимосвязи между «x» и «y», и продолжить исследования. Вторая процедура МНК. Определяется, какая линия (траектория) способна лучше всего описать или охарактеризовать тенденцию изменения урожайности подсолнечника за анализируемый период. При наличии компьютерной техники подбор оптимального тренда происходит автоматически. При «ручной» обработке выбор оптимальной функции осуществляется, как правило, визуальным способом – по расположению корреляционного поля. То есть, по виду графика подбирается уравнение линии, которая лучше всего подходит к эмпирическому тренду (к фактической траектории). Как известно, в природе существует огромное разнообразие функциональных зависимостей, поэтому визуальным способом проанализировать даже незначительную их часть — крайне затруднительно. К счастью, в реальной экономической практике большинство взаимосвязей достаточно точно могут быть описаны или параболой, или гиперболой, или же прямой линией. В связи с этим, при «ручном» варианте подбора лучшей функции, можно ограничиться только этими тремя моделями. Прямая: Гипербола: Парабола второго порядка: Нетрудно заметить, что в нашем примере лучше всего тенденцию изменения урожайности подсолнечника за анализируемые 10 лет характеризует прямая линия, поэтому уравнением регрессии будет уравнение прямой. Третья процедура. Рассчитываются параметры регрессионного уравнения, характеризующего данную линию, или другими словами, определяется аналитическая формула, описывающая лучшую модель тренда. Нахождение значений параметров уравнения регрессии, в нашем случае параметров Эта система уравнений довольно легко решается методом Гаусса. Напомним, что в результате решения, в нашем примере, находятся значения параметров В линейном уравнении параметр Приведем также системы нормальных уравнений для отыскивания параметров нелинейных уравнений. источники: http://be5.biz/ekonomika/e008/13.html http://www.ekonomstat.ru/lektsii-po-distsipline-statistika/31-kurs-lekcij-po-statistike/654-metod-naimenshih-kvadratov.html |





 ,
, — i-ые значения наблюдаемых показателей (для каждого показателя их n).
— i-ые значения наблюдаемых показателей (для каждого показателя их n).

 — расчетные значения,
— расчетные значения,  , тогда система нормальных уравнений получается из условия …
, тогда система нормальных уравнений получается из условия …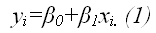
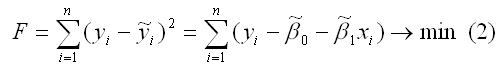
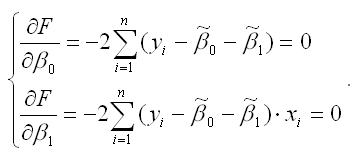 .
.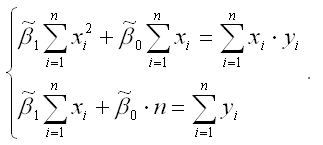
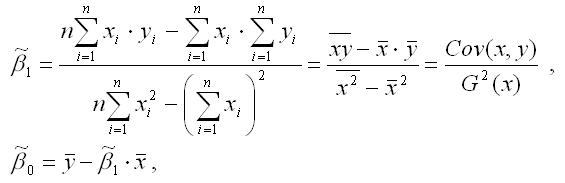
 (9.1)
(9.1) — квадратичное отклонение между наблюдаемой фактической величиной
— квадратичное отклонение между наблюдаемой фактической величиной — фактическое (наблюдаемое) значение изучаемого явления,
— фактическое (наблюдаемое) значение изучаемого явления, — расчетное значение модели тренда,
— расчетное значение модели тренда, — число наблюдений за изучаемым явлением.
— число наблюдений за изучаемым явлением.





 :
:
 и
и  , является сердцевиной МНК. Данный процесс сводится к решению системы нормальных уравнений.
, является сердцевиной МНК. Данный процесс сводится к решению системы нормальных уравнений. (9.2)
(9.2) и
и  . Таким образом, найденное уравнение регрессии будет иметь следующий вид:
. Таким образом, найденное уравнение регрессии будет иметь следующий вид: 
 с изменением
с изменением  на единицу. Он имеет единицу измерения результативного признака. В случае прямой связи
на единицу. Он имеет единицу измерения результативного признака. В случае прямой связи  при
при  . Если
. Если  не получает нулевых значений, этот параметр имеет лишь расчетное назначение.
не получает нулевых значений, этот параметр имеет лишь расчетное назначение.