Система нормальных уравнений и явный вид ее решения при оценивании методом наименьших квадратов линейной модели парной регрессии
Предположим, что в ходе регрессионного анализа была установлена линейная взаимосвязь между исследуемыми переменными х и у, которая описывается моделью регрессии вида:
В результате оценивания данной эконометрической модели определяются оценки неизвестных коэффициентов. Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК).
Метод наименьших квадратов позволяет получить такие оценки параметров β0и β1, при которых сумма квадратов отклонений фактических значений результативного признака y от расчетных (теоретических) y˜ минимальна:
В процессе минимизации функции (1) неизвестными являются только значения коэффициентов β0 и β1, потому что значения результативной и факторной переменных известны из наблюдений. Для определения минимума функции двух переменных вычисляются частные производные этой функции по каждому из оцениваемых параметров и приравниваются к нулю. Результатом данной процедуры будет стационарная система уравнений для функции (2):
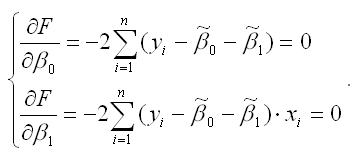
Если разделить обе части каждого уравнения системы на (-2), раскрыть скобки и привести подобные члены, то получим систему нормальных уравнений для функции регрессии вида yi=β0+β1xi:
Если решить данную систему нормальных уравнений, то мы получим искомые оценки неизвестных коэффициентов модели регрессии β0 и β1:
y – среднее значение зависимой переменной;
x – среднее значение независимой переменной;
xy – среднее арифметическое значение произведения зависимой и независимой переменных;
G 2 (x) – дисперсия независимой переменной;
Gcov (x, y) – ковариация между зависимой и независимой переменными.
Таким образом, явный вид решения системы нормальных уравнений может быть записан следующим образом:
Лекция. Метод наименьших квадратов (мнк) Оценка параметров линейных уравнений регрессии
| Название | Метод наименьших квадратов (мнк) Оценка параметров линейных уравнений регрессии |
| Анкор | Лекция |
| Дата | 30.06.2021 |
| Размер | 69 Kb. |
| Формат файла |  |
| Имя файла | 082_Lektsiya24_MNK.doc |
| Тип | Документы #222536 |
 С этим файлом связано 1 файл(ов). Среди них: Основые формы самостоятельных занятий.pdf. С этим файлом связано 1 файл(ов). Среди них: Основые формы самостоятельных занятий.pdf.  Показать все связанные файлы Подборка по базе: русский методика практич. 1.pdf, современные химические методы анализа.docx, Управление государственными и муниципальными финансами содержани, Медикаментозное лечение. Методичка.doc, Медиатексты, авторская оценка в СМИ. диплом.docx, Тема 2. Предмет и метод философии Семинар. зад.docx, математика методы.docx, русский методика преп. тест2.pdf, 12 04 04 Метод указания к выполнению магистерской диссертации.do, 6. Методы препарирования кариозных полостей.ppt Показать все связанные файлы Подборка по базе: русский методика практич. 1.pdf, современные химические методы анализа.docx, Управление государственными и муниципальными финансами содержани, Медикаментозное лечение. Методичка.doc, Медиатексты, авторская оценка в СМИ. диплом.docx, Тема 2. Предмет и метод философии Семинар. зад.docx, математика методы.docx, русский методика преп. тест2.pdf, 12 04 04 Метод указания к выполнению магистерской диссертации.do, 6. Методы препарирования кариозных полостей.pptМетод наименьших квадратов (МНК)Оценка параметров линейных уравнений регрессииПроцедура построения системы нормальных уравнений и исходное соотношение, используемое в МНК. Для определения параметров функции, используемой в эконометрической модели, разработаны различные методы, наиболее простым и известным из которых является метод наименьших квадратов (МНК). Рассмотрим суть этого метода на примере парной линейной регрессии. Применение МНК к парной линейной регрессии . Итак, необходимо определить параметры а и b для функции Чтобы построенная модель была как можно ближе к реальности, эта сумма должна быть как можно меньше. Отметим, что полученная сумма представляет собой функцию от двух переменных а и b, и чтобы найти ее минимум, приравняем к нулю ее частные производные по а и по b: Итак, получено два линейных уравнения с двумя неизвестными – а и b (система линейна относительно параметров регрессии). Такую систему называют системой нормальных уравнений. Решив ее, можно определить искомые параметры. где 1) методом Гаусса, который заключается в том, что матрицу коэффициентов в уравнениях поэтапно преобразуют в единичную матрицу путем линейных преобразований этих уравнений (разрешающее уравнение делят на разрешающий элемент, получая на его месте единицу, а из всех остальных уравнений вычитают преобразованное разрешающее, умноженное на те коэффициенты, которые стоят в этих уравнениях в разрешающем столбце, с целью получить на их месте нули); 2) методом Крамера, который заключается в том, что рассчитывают определитель матрицы коэффициентов в уравнениях, а затем рассчитывают частные определители, поочередно заменяя один из столбцов в этой матрице столбцом свободных членов; значения переменных равны отношениям соответствующих частных определителей к определителю первой матрицы; 3) методом обратной матрицы и т.д. Матричная форма МНКРассмотрим систему нормальных уравнений МНК, используя обозначения матричной алгебры. А именно, введем следующие обозначения: где m – число признаков-факторов, n — число наблюдений. Каждая строка матрицы соответствует одному из наблюдений, а каждый столбец, кроме первого, — одному из факторов. Если транспонировать матрицу X размерности n x (m + 1), в полученной матрице X Т размерности (m + 1) x n каждый столбец будет соответствовать одному из факторов, а строки — наблюдениям. Перемножив полученную матрицу X Т на X, получим симметричную матрицу размерности (m + 1) x (m + 1): Тогда система уравнений примет вид X Т XА = X Т Y. Умножим слева обе части этого выражения на матрицу (X Т X) -1 , получим: А = (X Т X) -1 X Т Y 2. Для нахождения параметров линейной регрессии минимизируют сумму квадратов отклонений фактических значений результата от подсчитанных по уравнению регрессии. Метод, в основе которого лежит эта идея, — метод … (напишите два слова в родительном падеже) 5. В модель множественной регрессии включено семь факторов. Сколько уравнений будет в системе нормальных уравнений? 7. В модель множественной регрессии включено три фактора. Сколько уравнений будет в системе нормальных уравнений? Метод наименьших квадратовНачнем статью сразу с примера. У нас есть некие экспериментальные данные о значениях двух переменных – x и y . Занесем их в таблицу.
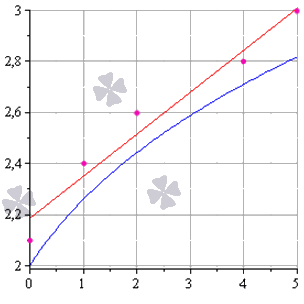
После выравнивания получим функцию следующего вида: g ( x ) = x + 1 3 + 1 . Мы можем аппроксимировать эти данные с помощью линейной зависимости y = a x + b , вычислив соответствующие параметры. Для этого нам нужно будет применить так называемый метод наименьших квадратов. Также потребуется сделать чертеж, чтобы проверить, какая линия будет лучше выравнивать экспериментальные данные. В чем именно заключается МНК (метод наименьших квадратов)Главное, что нам нужно сделать, – это найти такие коэффициенты линейной зависимости, при которых значение функции двух переменных F ( a , b ) = ∑ i = 1 n ( y i — ( a x i + b ) ) 2 будет наименьшим. Иначе говоря, при определенных значениях a и b сумма квадратов отклонений представленных данных от получившейся прямой будет иметь минимальное значение. В этом и состоит смысл метода наименьших квадратов. Все, что нам надо сделать для решения примера – это найти экстремум функции двух переменных. Как вывести формулы для вычисления коэффициентовДля того чтобы вывести формулы для вычисления коэффициентов, нужно составить и решить систему уравнений с двумя переменными. Для этого мы вычисляем частные производные выражения F ( a , b ) = ∑ i = 1 n ( y i — ( a x i + b ) ) 2 по a и b и приравниваем их к 0 . δ F ( a , b ) δ a = 0 δ F ( a , b ) δ b = 0 ⇔ — 2 ∑ i = 1 n ( y i — ( a x i + b ) ) x i = 0 — 2 ∑ i = 1 n ( y i — ( a x i + b ) ) = 0 ⇔ a ∑ i = 1 n x i 2 + b ∑ i = 1 n x i = ∑ i = 1 n x i y i a ∑ i = 1 n x i + ∑ i = 1 n b = ∑ i = 1 n y i ⇔ a ∑ i = 1 n x i 2 + b ∑ i = 1 n x i = ∑ i = 1 n x i y i a ∑ i = 1 n x i + n b = ∑ i = 1 n y i Для решения системы уравнений можно использовать любые методы, например, подстановку или метод Крамера. В результате у нас должны получиться формулы, с помощью которых вычисляются коэффициенты по методу наименьших квадратов. n ∑ i = 1 n x i y i — ∑ i = 1 n x i ∑ i = 1 n y i n ∑ i = 1 n — ∑ i = 1 n x i 2 b = ∑ i = 1 n y i — a ∑ i = 1 n x i n Мы вычислили значения переменных, при который функция Это и есть применение метода наименьших квадратов на практике. Его формула, которая применяется для поиска параметра a , включает в себя ∑ i = 1 n x i , ∑ i = 1 n y i , ∑ i = 1 n x i y i , ∑ i = 1 n x i 2 , а также параметр Обратимся вновь к исходному примеру. Здесь у нас n равен пяти. Чтобы было удобнее вычислять нужные суммы, входящие в формулы коэффициентов, заполним таблицу.
Решение Четвертая строка включает в себя данные, полученные при умножении значений из второй строки на значения третьей для каждого отдельного i . Пятая строка содержит данные из второй, возведенные в квадрат. В последнем столбце приводятся суммы значений отдельных строчек. Воспользуемся методом наименьших квадратов, чтобы вычислить нужные нам коэффициенты a и b . Для этого подставим нужные значения из последнего столбца и подсчитаем суммы: n ∑ i = 1 n x i y i — ∑ i = 1 n x i ∑ i = 1 n y i n ∑ i = 1 n — ∑ i = 1 n x i 2 b = ∑ i = 1 n y i — a ∑ i = 1 n x i n ⇒ a = 5 · 33 , 8 — 12 · 12 , 9 5 · 46 — 12 2 b = 12 , 9 — a · 12 5 ⇒ a ≈ 0 , 165 b ≈ 2 , 184 У нас получилось, что нужная аппроксимирующая прямая будет выглядеть как y = 0 , 165 x + 2 , 184 . Теперь нам надо определить, какая линия будет лучше аппроксимировать данные – g ( x ) = x + 1 3 + 1 или 0 , 165 x + 2 , 184 . Произведем оценку с помощью метода наименьших квадратов. Чтобы вычислить погрешность, нам надо найти суммы квадратов отклонений данных от прямых σ 1 = ∑ i = 1 n ( y i — ( a x i + b i ) ) 2 и σ 2 = ∑ i = 1 n ( y i — g ( x i ) ) 2 , минимальное значение будет соответствовать более подходящей линии. σ 1 = ∑ i = 1 n ( y i — ( a x i + b i ) ) 2 = = ∑ i = 1 5 ( y i — ( 0 , 165 x i + 2 , 184 ) ) 2 ≈ 0 , 019 σ 2 = ∑ i = 1 n ( y i — g ( x i ) ) 2 = = ∑ i = 1 5 ( y i — ( x i + 1 3 + 1 ) ) 2 ≈ 0 , 096 Ответ: поскольку σ 1 σ 2 , то прямой, наилучшим образом аппроксимирующей исходные данные, будет Как изобразить МНК на графике функцийМетод наименьших квадратов наглядно показан на графической иллюстрации. С помощью красной линии отмечена прямая g ( x ) = x + 1 3 + 1 , синей – y = 0 , 165 x + 2 , 184 . Исходные данные обозначены розовыми точками. Поясним, для чего именно нужны приближения подобного вида. Они могут быть использованы в задачах, требующих сглаживания данных, а также в тех, где данные надо интерполировать или экстраполировать. Например, в задаче, разобранной выше, можно было бы найти значение наблюдаемой величины y при x = 3 или при x = 6 . Таким примерам мы посвятили отдельную статью. Доказательство метода МНКЧтобы функция приняла минимальное значение при вычисленных a и b , нужно, чтобы в данной точке матрица квадратичной формы дифференциала функции вида F ( a , b ) = ∑ i = 1 n ( y i — ( a x i + b ) ) 2 была положительно определенной. Покажем, как это должно выглядеть. У нас есть дифференциал второго порядка следующего вида: d 2 F ( a ; b ) = δ 2 F ( a ; b ) δ a 2 d 2 a + 2 δ 2 F ( a ; b ) δ a δ b d a d b + δ 2 F ( a ; b ) δ b 2 d 2 b Решение δ 2 F ( a ; b ) δ a 2 = δ δ F ( a ; b ) δ a δ a = = δ — 2 ∑ i = 1 n ( y i — ( a x i + b ) ) x i δ a = 2 ∑ i = 1 n ( x i ) 2 δ 2 F ( a ; b ) δ a δ b = δ δ F ( a ; b ) δ a δ b = = δ — 2 ∑ i = 1 n ( y i — ( a x i + b ) ) x i δ b = 2 ∑ i = 1 n x i δ 2 F ( a ; b ) δ b 2 = δ δ F ( a ; b ) δ b δ b = δ — 2 ∑ i = 1 n ( y i — ( a x i + b ) ) δ b = 2 ∑ i = 1 n ( 1 ) = 2 n Иначе говоря, можно записать так: d 2 F ( a ; b ) = 2 ∑ i = 1 n ( x i ) 2 d 2 a + 2 · 2 ∑ x i i = 1 n d a d b + ( 2 n ) d 2 b . Мы получили матрицу квадратичной формы вида M = 2 ∑ i = 1 n ( x i ) 2 2 ∑ i = 1 n x i 2 ∑ i = 1 n x i 2 n . В этом случае значения отдельных элементов не будут меняться в зависимости от a и b . Является ли эта матрица положительно определенной? Чтобы ответить на этот вопрос, проверим, являются ли ее угловые миноры положительными. Вычисляем угловой минор первого порядка: 2 ∑ i = 1 n ( x i ) 2 > 0 . Поскольку точки x i не совпадают, то неравенство является строгим. Будем иметь это в виду при дальнейших расчетах. Вычисляем угловой минор второго порядка: d e t ( M ) = 2 ∑ i = 1 n ( x i ) 2 2 ∑ i = 1 n x i 2 ∑ i = 1 n x i 2 n = 4 n ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2 После этого переходим к доказательству неравенства n ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2 > 0 с помощью математической индукции.
2 ∑ i = 1 2 ( x i ) 2 — ∑ i = 1 2 x i 2 = 2 x 1 2 + x 2 2 — x 1 + x 2 2 = = x 1 2 — 2 x 1 x 2 + x 2 2 = x 1 + x 2 2 > 0 У нас получилось верное равенство (если значения x 1 и x 2 не будут совпадать).
( n + 1 ) ∑ i = 1 n + 1 ( x i ) 2 — ∑ i = 1 n + 1 x i 2 = = ( n + 1 ) ∑ i = 1 n ( x i ) 2 + x n + 1 2 — ∑ i = 1 n x i + x n + 1 2 = = n ∑ i = 1 n ( x i ) 2 + n · x n + 1 2 + ∑ i = 1 n ( x i ) 2 + x n + 1 2 — — ∑ i = 1 n x i 2 + 2 x n + 1 ∑ i = 1 n x i + x n + 1 2 = = ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2 + n · x n + 1 2 — x n + 1 ∑ i = 1 n x i + ∑ i = 1 n ( x i ) 2 = = ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2 + x n + 1 2 — 2 x n + 1 x 1 + x 1 2 + + x n + 1 2 — 2 x n + 1 x 2 + x 2 2 + . . . + x n + 1 2 — 2 x n + 1 x 1 + x n 2 = = n ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2 + + ( x n + 1 — x 1 ) 2 + ( x n + 1 — x 2 ) 2 + . . . + ( x n — 1 — x n ) 2 > 0 Выражение, заключенное в фигурные скобки, будет больше 0 (исходя из того, что мы предполагали в пункте 2 ), и остальные слагаемые будут больше 0 , поскольку все они являются квадратами чисел. Мы доказали неравенство. Ответ: найденные a и b будут соответствовать наименьшему значению функции F ( a , b ) = ∑ i = 1 n ( y i — ( a x i + b ) ) 2 , значит, они являются искомыми параметрами метода наименьших квадратов (МНК). источники: http://topuch.ru/metod-naimeneshih-kvadratov-mnk-ocenka-parametrov-linejnih-ura/index.html http://zaochnik.com/spravochnik/matematika/stati/metod-naimenshih-kvadratov/ |
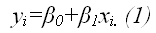
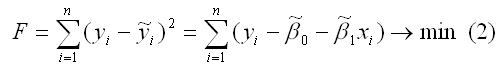
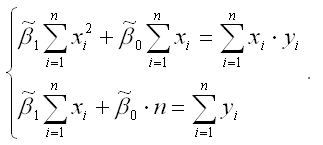
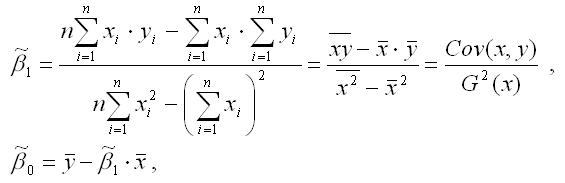





 ,
, — i-ые значения наблюдаемых показателей (для каждого показателя их n).
— i-ые значения наблюдаемых показателей (для каждого показателя их n).

 — расчетные значения,
— расчетные значения,  , тогда система нормальных уравнений получается из условия …
, тогда система нормальных уравнений получается из условия …