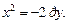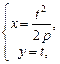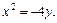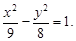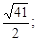Параметры параболы
Точка F(p/2, 0) называется фокусомпараболы, величина p – параметром, точка О(0, 0) – вершиной (рис. 9.15). При этом прямая OF, относительно которой парабола симметрична, задает ось этой кривой.
Величина 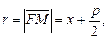
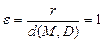
Основное характеристическое свойство параболы: все точки параболы равноудалены от директрисы и фокуса (рис. 9.15).
Существуют иные формы канонического уравнения параболы, которые определяют другие направления ее ветвей в системе координат (рис. 9.16):
а) 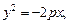
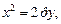
Для параметрического задания параболы в качестве параметра t может быть взята величина ординаты точки параболы:
где t – произвольное действительное число.
Пример 1.Определить параметры и форму параболы по ее каноническому уравнению:
1) 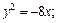
Решение.1) Уравнение y 2 = –8x определяет параболу с вершиной в точке О(0; 0), симметричную относительно оси Оx. Ее ветви направлены влево. Сравнивая данное уравнение с уравнением y 2 = –2px, находим: 2p = 8, p = 4, p/2 = 2. Следовательно, фокус находится в точке F(–2; 0), уравнение директрисы D: x = 2 (рис. 9.17).
2) Уравнение x 2 = –4y задает параболу с вершиной в точке O(0; 0), симметричную относительно оси Oy. Ее ветви направлены вниз. Сравнивая данное уравнение с уравнением x 2 = –2py, находим: 2p = 4, p = 2, p/2 = 1. Следовательно, фокус находится в точке F(0; –1), уравнение директрисы D: y = 1 (рис. 9.18).
Пример 2.Определить параметры и вид кривой x 2 + 8x – 16y – 32 = 0. Сделать рисунок.
Решение. Преобразуем левую часть уравнения, используя метод выделения полного квадрата:
(x + 4) 2 – 16 – 16y – 32 = 0;
В результате получим:
Это каноническое уравнение параболы с вершиной в точке (–4; –3), параметром p = 8, ветвями, направленными вверх 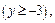
Пример 3. Написать уравнение кривой, все точки которой равноудалены от прямой y = –3 и точки F(0; 3).
Решение. Точка F(0; 3) лежит на оси Oy и находится с прямой y = –3 по разные стороны от начала координат, причем на одинаковом расстоянии (d = 3). Это позволяет заключить, что искомой кривой является парабола x 2 = 2py с параметром p = 2 × 3 = 6, т. е. x 2 = 12y (рис. 9.20).
Пример 4.Составить уравнение параболы с вершиной в точке V(3; –2) и фокусом в точке F(1; –2).
Решение. Вершина и фокус данной параболы лежат на прямой, параллельной оси Ox (одинаковые ординаты), ветви параболы направлены влево (абсцисса фокуса меньше абсциссы вершины), расстояние от фокуса до вершины равно p/2 = 3 – 1 = 2, p = 4. Следовательно, искомое уравнение
Дата добавления: 2015-09-29 ; просмотров: 8110 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Кривые второго порядка
Эллипсом называется множество точек плоскости, сумма расстояний от каждой из которых до двух данных, называемых фокусами, есть величина постоянная, равная 2a, и большая чем расстояние между фокусами, равное 2c (рисунок 6).
 |
| Рисунок 6 |
Простейшее каноническое уравнение эллипса получается в системе координат, в которой за ось абсцисс выбрана прямая, соединяющая фокусы, начало координат 0 − середина отрезка, концами которого служат фокусы, ось ординат – прямая, проходящая перпендикулярно оси ОX через точку 0. Тогда уравнение эллипса примет следую-
щий вид:
где
При таком выборе системы координат оси координат совпадают с осями симметрии эллипса, а начало координат − с центром симметрии. Точки А1(a; 0), А2(–a; 0), В1(0; b), В2(0; –b) называются вершинами эллипса. Отрезки, заключенные между вершинами, называются осями эллипса: большая (фокальная) ось А1А2 = 2a, малая ось В1В2 = 2b. Параметры a и b уравнения равны полуосям эллипса. Эксцентриситетом (e) эллипса называется отношение расстояния (2c) между фокусами к большей оси (2a), т. е. 
Ответ:
Тест 22. Уравнение эллипса, полуоси которого равны a = 3, b = 2, имеет вид:
1)
2)
3)
Тест 23. Дано уравнение эллипса
Вычислить длину осей, фокусное расстояние, эксцентриситет:
1) 16; 9; 25;
2) 8; 6; 2
Пример 12. Дан эллипс 
Уравнения директрис следующие: 
b 2 = 20. Следовательно, a = 6, 

Уравнение эллипса, центр которого находится в точке (х0; у0), а оси симметрии параллельны осям координат, имеет вид
Тест 24. Центр эллипса 
Гиперболой называется множество точек плоскости, модуль разности от каждой из которых до двух данных точек, называемых фокусами, есть величина постоянная, равная 2a, и меньшая чем расстояние между фокусами, равное 2c (рисунок 7).
 |
Простейшее каноническое уравнение гиперболы имеет вид

Прямая, соединяющая фокусы F1, F2 гиперболы, служит осью абсцисс, начало координат находится в середине между фокусами; при этом оси координат совпадают с осями симметрии гиперболы, начало координат – с ее центром симметрии (оси и центр гиперболы).
Гипербола имеет две действительные вершины А1(a; 0), А2(–a; 0) на фокальной оси; отрезок А1А2 = 2a называется действительной осью гиперболы, отрезок В1В2 = 2b – мнимой осью гиперболы. Таким образом, параметры a и b в уравнении гиперболы равны длинам действительной и мнимой полуосей соответственно.
Если a = b, то гипербола называется равносторонней.
Если мнимая ось гиперболы имеет длину 2a и направление по оси x, а действительная ось, длиной 2b, совпадает с осью y, то уравнение такой гиперболы имеет следующий вид:

где
Гиперболы (1) и (2) называются сопряженными гиперболами.
Эксцентриситетом гиперболы называется отношение расстояния между фокусами к действительной оси: e = 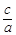


Если точка, двигаясь по гиперболе, неограниченно удаляется, то расстояние ее от одной из асимптот стремится к нулю. Асимптоты являются диагоналями прямоугольника со сторонами 2a, 2b (рисунок 7).
Пример 13.Составить уравнение гиперболы, оси которой совпадают с осями координат, зная, что:
1. Расстояние между вершинами равно 8, а расстояние между фокусами – 10.
2. Действительная ось равна 6, гипербола проходит через точку
(9; –4).
1. Уравнение гиперболы имеет вид
Так как расстояние между вершинами равно 8, то 2a = 8 или a = 4. Учитывая, что расстояние между фокусами равно 10, имеем 2c = 10, откуда c = 5. Найдем b 2 из соотношения b 2 = c 2 – а 2 , т. е. b 2 = 5 2 – 4 2 =
= 25 – 16 = 9.
Ответ:
2. Так как действительная ось равна 6, то 2a = 6 или a =3. Поэтому уравнение гиперболы принимает вид 




Ответ:
Тест 25. Уравнение гиперболы, действительная ось которой равна 10 и лежит на оси ОX, а мнимая ось равна 16 и лежит на оси ОY, имеет вид:
1)
2)
3)
Тест 26. Дано уравнение гиперболы 
1) 10; 16; 2
2) 4; 5;
3) 5; 4;
Пример 14. Дана гипербола 
Из уравнения а 2 = 16, b 2 = 25. Откуда a =4, b =5. Найдем 


Уравнения асимптот 
Ответ: x = 
Тест 27. Указать, принадлежит ли точка (0; 2) гиперболе 
Уравнение гиперболы, центр которой находится в точке (х0; у0), действительная ось совпадает с осью ОX, мнимая – с осью ОY, имеет вид
Тест 28. Центр гиперболы 
Ответы на тестовые задания
| Номер теста |
| Правильный ответ |
Парабола
Параболой называется геометрическое место точек, равноудаленных от данной точки, называемой фокусом параболы, и данной прямой, называемой директрисой параболы (рисунок 8).
 |
| Рисунок 8 |
Если за ось абсцисс принять перпендикулярную прямую, проведенную из фокуса к директрисе, а начало координат поместить посередине между фокусом и директрисой, то уравнение параболы примет вид
где р – параметр параболы, расстояние от фокуса параболы до ее директрисы.
Парабола имеет одну ось симметрии, которая совпадает при таком выборе системы координат с осью X. Единственная вершина параболы совпадает с началом координат и является единственной точкой пересечения параболы с осями.
Пример 15. Составить уравнение параболы, зная, что фокусы имеют координаты (0; 5), ось ординат служит осью симметрии, а вершина находится в начале координат.
Так как осью симметрии является ось ОY, то уравнение будет иметь вид х 2 = 2ру, так как фокус в общем случае имеет координаты 

Тест 29. В уравнении параболы у 2 = 3х значение параметра p равно:
2) 
Тест 30. Среди уравнений второго порядка указать уравнение гиперболы:
1)
2)
3)
Если вершина параболы находится в точке (x0; y0), то ее каноническое уравнение примет следующий вид:
Ответы на тестовые задания
| Номер теста |
| Правильный ответ |
Векторная алгебра
При изучении различных разделов экономики, механики, физики, других учебных дисциплин приходится иметь дело с величинами, для характеризации которых в выбранной системе единиц достаточно указать их численные значения. Эти величины называются скалярными. К числу скалярных величин можно отнести длину, площадь, объем, массу, температуру и т. п. Встречаются, тем не менее, такие величины, для определения которых необходимо знать их направления в пространстве. Указанные величины будем называть векторными. Примерами векторных величин являются сила, скорость, ускорение.
Геометрические векторные величины изображаются с помощью направленных отрезков.
Связанным вектором (или направленным отрезком) называется любой отрезок прямой, если только указано, какая из двух ограничивающих его точек является начальной, какая – конечной. Если точка А – начало отрезка, а точка В – его конец, то связанный вектор будем обозначать 
Длиной 
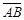

Связанные векторы 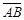


Два ненулевых связанных вектора 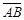

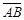

Свободным вектором а (или просто вектором) назовем множество равных между собой связанных векторов. При дальнейшем из контекста будет ясно, какой вектор имеется в виду (связанный или свободный). Для задания вектора достаточно указать какой-либо один вектор из всего множества <AB, CD, MN, ¼> равных связанных векторов, например, 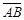
Рассмотренные понятия (длина, направление и т. п.), которые введены для связанных векторов, имеют аналоги также и для свободных. Часто векторы обозначают одной жирной строчной буквой: 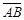
Линейные операции над векторами
Определим для свободных векторов операции их сложения, вычитания, умножения вектора на действительное число.
Суммой двух векторов a и b по правилу треугольника называется такой третий вектор с, что начало его совпадает с началом вектора а, а конец – с концом вектора b.
Иногда вместо с = а+bпишут 
… + аn конечного числа векторов называется такой вектор а, который замыкает ломаную линию, построенную из данных векторов а1, а2,…, аn таким образом, что начало каждого последующего вектора совпадает с концом предыдущего. Указанный вектор а направлен из начала первого вектора суммы в конец последнего (правило многоугольника) (рисунок 10).
c = a + b
На рисунке 11 изображена сумма а = а1 + а2 + а3 + а4 + а5 векторов а1, а2, а3, а4, а5.
Произведением вектора а на число a называется вектор b = a а, длина которого равна 
a 0 будем обозначать единичный вектор, имеющий направление вектора а.
Квадратичная функция. Построение параболы
О чем эта статья:
8 класс, 9 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные понятия
Функция — это зависимость «y» от «x», при которой «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.
Задать функцию означает определить правило в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
- Табличный способ. Помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
- Графический способ: наглядно.
- Аналитический способ, через формулы. Компактно и можно посчитать функцию при произвольном значении аргумента из области определения.
- Словесный способ.
График функции — это объединение всех точек, когда вместо «x» можно подставить в функцию произвольные значения и найти координаты этих точек.
Еще быстрее разобраться в теме и научиться строить график квадратичной функции можно на курсах по математике в онлайн-школе Skysmart.
Построение квадратичной функции
Квадратичная функция задается формулой y = ax 2 + bx + c, где x и y — переменные, a, b, c — заданные числа, обязательное условие — a ≠ 0. В уравнении существует следующее распределение:
|
График квадратичной функции — парабола, которая имеет следующий вид для y = x 2 :
Точки, обозначенные зелеными кружками называют базовыми точками. Чтобы найти их координаты для функции y = x 2 , нужно составить таблицу:
x
y
Если в уравнении квадратичной функции старший коэффициент равен единице, то график имеет ту же форму, как y = x 2 при любых значениях остальных коэффициентов.
График функции y = –x 2 выглядит, как перевернутая парабола:
Зафиксируем координаты базовых точек в таблице:
x
y
Посмотрев на оба графика можно заметить их симметричность относительно оси ОХ. Отметим важные выводы:
- Если старший коэффициент больше нуля a > 0, то ветви параболы напрaвлены вверх.
- Если старший коэффициент меньше нуля a 2 + bx + c, для построения которой нужно решить квадратное уравнение ax 2 + bx + c = 0. В процессе найдем дискриминант D = b 2 — 4ac, который даст нам информацию о количестве корней квадратного уравнения.
Рассмотрим три случая:
- Если D 0,то график выглядит так:
- Если D = 0, то уравнение имеет одно решение, а парабола пересекает ось ОХ в одной точке. Если a > 0, то график имеет такой вид:
- Если D > 0, то уравнение имеет два решения, а парабола пересекает ось ОХ в двух точках, которые можно найти следующим образом:
Если a > 0, то график выглядит как-то так:
0″ height=»671″ src=»https://lh6.googleusercontent.com/8ryBuyxmK9S2EbnsNc4AE5PEl_NpIg0RAM_Y_V8wUP-zREEHNgi9QoQTl8FXxoujjWRAvf3s-MPRsXsoepaLLSTHDX-ReGtrsnLQp4dW3WaEyPF2ywjVpYFXlDIpAEHoIiwlxiB7″ width=»602″>
На основе вышеизложенного ясно, что зная направление ветвей параболы и знак дискриминанта, у нас есть понимание, как будет выглядеть график конкретной функции.
Координаты вершины параболы также являются важным параметром графика квадратичной функции и находятся следующим способом:
Ось симметрии параболы — прямая, которая проходит через вершину параболы параллельно оси OY.
Чтобы построить график, нам нужна точка пересечения параболы с осью OY. Так как абсцисса каждой точки оси OY равна нулю, чтобы найти точку пересечения параболы y = ax 2 + bx + c с осью OY, нужно в уравнение вместо х подставить ноль: y(0) = c. То есть координаты этой точки будут соответствовать: (0; c).
На изображении отмечены основные параметры графика квадратичной функции:
Алгоритм построения параболы
Рассмотрим несколько способов построения квадратичной параболы. Наиболее удобный способ можно выбрать в соответствии с тем, как задана квадратичная функция.
Уравнение квадратичной функции имеет вид y = ax 2 + bx + c.
Разберем общий алгоритм на примере y = 2x 2 + 3x — 5.
Как строим:
- Определим направление ветвей параболы. Так как а = 2 > 0, ветви параболы направлены вверх.
- Найдем дискриминант квадратного трехчлена 2x 2 + 3x — 5.
D = b 2 — 4ac = 9 — 4 * 2 * (-5) = 49 > 0
В данном случае дискриминант больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ. Чтобы найти их координаты, решим уравнение:
2x 2 + 3x — 5 = 0 2 + 3x — 5 = 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAPoAAAAyCAYAAAB1V8bkAAAJyElEQVR4Ae2c16sUwRLGfdRX/wXFB30QFFQUQUyIKCIGBEEQzCCoKIgB01ExZwVz4JpzztljwJxzzjlnrcuvL33unD2zOzO7OzvuThU0u5N6uuvrr7u6unrKiYpqQDVQ8BooV/A11AqqBlQDokTXRqAaiIEGlOgxAFmrqBpQomsbUA3EQANK9BiArFVUDSjRtQ2oBmKgASV6DEDWKqoGlOjaBlQDMdBAQRH9z58/8vv3b5P+/v2bMXy/fv0S8kxMGWesGRgNpIMXz7jhkg28CxmWgiH69+/f5dSpU7JixQpZtmyZXLx4UX7+/JkUOxoGjSaVTJw4UVatWiUbNmwoSYcPH071iF7zqYGgeNlsT58+LZMnTy7BA2y2bNkib9++tbfor4sGCobogD19+nR5/fq1nDx5Upo0aSLHjh2TZD39x48f5ebNmy4q+d8pRo327dtLo0aNTF6NGzeWevXqCeRXyVwDQfHijXTMmzZtMjiAL6lu3brSuXNnuXfvXuaFKuAcCobojOQDBgwwgD948EAg5ubNm42Z54bfjRs3ZMqUKW6XzDk6jP379wsjD/LmzRtZt26dvHr1KukzesG/BoLiRc5gceXKFZM4/vbtmxw6dEguXbokP3788P/yGN5ZMET/8uWLvHv3Tt6/f2/Muh49esj169eTQupF9MQHIfm1a9cST+txmhoIipfba86fPy9Hjx4VrDOV1BooGKJTTYh++fJlGTt2rCxevNgcJ6t+EKIz3587d26yrPR8mhoIglfiK549e2Y6dHBU8dZA3hH9+PHjYhNmnFO+fv1qTOwDBw5Ily5dhF+nQ47ndu/ebdLChQule/fuJcecp9E477d5d+zYUW7fvm0P9TeABixW/AbBCz+LffbChQtl3rh69WpZsmSJjuZlNON+Iu+IDkGZW+N427Ztm6nVp0+f5MiRI6Zh2Dl1hw4dZOjQoaVGdebc1oM+a9Ys48Sxx/y6zfUePnwoVapUcdeenvXUQLp4LV261OA8bdo0g5nzRR8+fJBhw4YJeav400DeEf3Ro0dmZGD+/fLlS1NLzLjhw4fLmDFjhEaA4DHv16+fGeHdVOHXdKczqVy5slsWes6HBtLF6/HjxwZn/CLPnz8v9aZbt25Jt27dlOiltJL6IO+I7lYdTPY1a9bIjBkz5M6dO7Jjxw5hRN++fXtSb6xfos+ZM0cqVark9trQzrEmXFxc7LnOH1oBQs44HbycRTpz5oy0a9funyA6DkGW/NavX19mauIsc+J/OkCmJliRL168ME7FVM7jxOeDHhcE0ak05KD3P3v2rFkWO3HihHz+/DmpPlh3XbRoUdLr9gL5LF++3B6G+nv//n3ZuHGjDBw4UDp16pS0kwq1EDnKPChezmI9efJEtm7dmnJVxXl/WP8PHjxopoxXr141RG3Tpo0JsPLzPqaaLVq0kDp16kjDhg2lb9++JgbEz7Pp3FMwRKfyBLkwX2fpxivqjbm8Nf1TKY77WK/NhVBuGvGoUaNMHID1N+Ti3VG8IwhezvIR5gwm/EYlrBgMGTJE9u3bZxy4YDV69Gjf/py9e/fKypUrjSVKLEDYqwcFRfSoQM/2e2fOnGmivgqd6NnWWy7zI3CqefPmUlRUVOIXgrzly5cXfEZewr2Y/XTuyaI3vfIIcj1tolM4lpyIBZ83b56MGzdO9uzZY0YjwkSfPn0apBx6r0MDYRBd8XIoOAt/sRiZU0N4az2OHz9eKlSo4MvSgOgs6RKIBYdIYUraRMfsYpkL84m5cc+ePY1DYv78+dKnTx/B2eAlmKldu3b1TISy5luII8s/XnWbNGmSMC9PlDCIrniJcXB6YcJ15s9+JHEkrlq1qixYsMDPowLRcRqzSgSHiOkI0xeUNtHpxXBUIQQ3tGrVKnLniC8N58FNYRBd8QoOPES2Php8Agw2dvR25gZRcaaNHDnSeTrlf/JxdhTsuMQacJ5LmUHAi2kT3b6HyrNBoXXr1uYUBXVThr3f+YuCcGp4JZRsFYAV8K8lt1hremqveuE4RAeJEgbR7Tvigpfb1JG6e2HCde5DCJbCM16rVi2T2D9BiLVT6Agwv3GsgSXPumHqfAZ+sLqCNWfbNQ455ve8MwxJm+gsXeF0YFcXPRlRaAiebD/OCO5l/XDQoEGeCTPHhqZWq1ZN/rVElF2iTJ061bNemHkEhiRKGESPG141atRIVKtZevXT3tjz7kcYgIioZDRmtyM6Zk09sf0zbYIndkBgabFt27ZmeZeYAgQzvmLFimWe9VMOP/ekTXTWMXv37m16uF69esmECRNMZdgDzgcgVIJrwLm8Vr9+fSECjM4wG6J4ZUOL/8+DgQdSwwGccIRkk4jITBRGaZZM8V/ZlRRGdIJlwJzBsX///gKPwpK0iY7HkArSgKgwu8XYMnju3LmkgSr0ZNZUCatCfvLFtKIHtj2sn2dycY8NmCGcF6cQIwXx+dmQfMMLfEj/qjA1Yx29ZcuWpRLmfaLcvXtXBg8eLCNGjChxUoM1mBAdt3btWmP9ZatTT3w/x2kTHcKytAB5EeYmyYiDecpWz9mzZyf9EIRb4cI6Rw/KikGcLI98w4vlWkKYC0Uw5xkEMeGt4A/Akc28P+wBMG2i28L6+WV7IruRmjVrVmK6+HkujHuYL+3atcuUhbm/SlkNRI0Xn/iqWbOmaTNlS5d/ZzDzITOhslFJTohO5Rg98WDaOUoUFabXpBExV2JThBI9OQpR4YX1x3SQb/UxOBSCYO2yA48RPCqJFdGZmxN8w/q/Ej11k4uK6ERXMqflw4+FQvTUms7N1VgRnYgndq2RlOipG1gURCf2myhLpldNmzZVoqeGKNDV2BAdj+bOnTuNcpTo3m0k10THrCVohCAiRInujVGQO2JDdJYA8bQTpIJHt3bt2mZtk1FEpawGck10PrRB4BEf4QQjgqIIK2UbqErmGsgJ0fE2AmL16tWFj/oRwpprYcRgVCcR+URsPkELBCyolNZAFHgRVcZyrcWoQYMGwtd97KfBSpdQj4JqICdEZ3kBkwwQIZZXLHDQSvi9H687G/wJgyREkl+7McdvHnG4L0q8WG9mUOCDnASf4DxVyVwDOSF65sXMXg6QnYbMMh+/fjfgZK8EmlMqDYAPzji7WyyqQSFVGfPxWuyIno8gaZlVA5lqQImeqQb1edVAHmhAiZ4HIGkRVQOZakCJnqkGI3m+WIrKlZOi45G8XF+ahxpQouchaKbIx4uU6PmKXQTlVqJHoPTMX/lM/tOuSIozz0hziIkGlOgxAVqrGW8NKNHjjb/WPiYaUKLHBGitZrw1oESPN/5a+5hoQIkeE6C1mvHWwH8BSUfSiO3XWNEAAAAASUVORK5CYII=»>
- Координаты вершины параболы:
- Точка пересечения с осью OY находится: (0; -5) и ей симметричная.
- Нанести эти точки на координатную плоскость и построить график параболы:
2 + 3x — 5 = 0″ height=»671″ src=»https://lh6.googleusercontent.com/TYyA5dFfh0ZKINaPSps3Y_X1mCv8Mhv_8bNG3_dPbZud1AEsvo7UBFmVQNm1GcR1CQFo6HE1lNjYaAgepQUTQiK_ay_Fnuv7LEsB53woHkFO66W0R1PP8QfGsFcYzaR_h4AJdLxC» width=»602″>
Уравнение квадратичной функции имеет вид y = a * (x — x₀) 2 + y₀
Координаты его вершины: (x₀; y₀). В уравнении квадратичной функции y = 2x 2 + 3x — 5 при а = 1, то второй коэффициент является четным числом.
Рассмотрим пример: y = 2 * (x — 1) 2 + 4.
Как строим:
- Воспользуемся линейным преобразованием графиков функций. Для этого понадобится:
- построить y = x 2 ,
- умножить ординаты всех точек графика на 2,
- сдвинуть его вдоль оси ОХ на 1 единицу вправо,
- сдвинуть его вдоль оси OY на 4 единицы вверх.
- Построить график параболы для каждого случая. 2 + y₀» height=»431″ src=»https://lh5.googleusercontent.com/_zgF-CXWf4Yy0p2OnBYSJkUm0zO-mNetq5feU6LIPEbIgSrO9kdr2ti_tr7Gg3yTMOlJVnuZgG0HleAFfAzG7yr7ELHT6KSMqMrRHkHqt-VcgIiSZx80cVj0zlPMBzEM0wAWQ-L6″ width=»602″>
Уравнение квадратичной функции имеет вид y = (x + a) × (x + b)
Рассмотрим следующий пример: y = (x − 2) × (x + 1).
Как строим:
Данный вид уравнения позволяет быстро найти нули функции:
(x − 2) × (x + 1) = 0, отсюда х₁ = 2, х₂ = −1.
Определим координаты вершины параболы:
Найти точку пересечения с осью OY:
с = ab = (−2) × (1) = −2 и ей симметричная.
Отметим эти точки на координатной плоскости и соединим плавной прямой.
http://megaobuchalka.ru/7/28566.html
http://skysmart.ru/articles/mathematic/kvadratichnaya-funkciya-parabola