Вариант 1 решите уравнения 1 3х 12

Решение задач по математике онлайн

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Калькулятор онлайн.
Решение показательных уравнений.

Этот математический калькулятор онлайн поможет вам решить показательное уравнение. Программа для решения показательного уравнения не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс получения результата.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Обязательно ознакомьтесь с правилами ввода функций. Это сэкономит ваше время и нервы.
Правила ввода функций >> Почему решение на английском языке? >> С 9 января 2019 года вводится новый порядок получения подробного решения некоторых задач. Ознакомтесь с новыми правилами >> —> Введите показательное уравнение
Решить уравнение

Немного теории.

Показательная функция, её свойства и график

Напомним основные свойства степени. Пусть а > 0, b > 0, n, m — любые действительные числа. Тогда
1) a n a m = a n+m

4) (ab) n = a n b n

7) a n > 1, если a > 1, n > 0

8) a n m , если a > 1, n n > a m , если 0 x , где a — заданное положительное число, x — переменная. Такие функции называют показательными. Это название объясняется тем, что аргументом показательной функции является показатель степени, а основанием степени — заданное число.

Определение. Показательной функцией называется функция вида y = a x , где а — заданное число, a > 0, \( a \neq 1\)

Показательная функция обладает следующими свойствами

1) Область определения показательной функции — множество всех действительных чисел.
Это свойство следует из того, что степень a x где a > 0, определена для всех действительных чисел x.

2) Множество значений показательной функции — множество всех положительных чисел.
Чтобы убедиться в этом, нужно показать, что уравнение a x = b, где а > 0, \( a \neq 1\), не имеет корней, если \( b \leqslant 0\), и имеет корень при любом b > 0.

3) Показательная функция у = a x является возрастающей на множестве всех действительных чисел, если a > 1, и убывающей, если 0 x при a > 0 и при 0 x при a > 0 проходит через точку (0; 1) и расположен выше оси Oх.
Если х x при a > 0.
Если х > 0 и |х| увеличивается, то график быстро поднимается вверх.

График функции у = a x при 0 0 и увеличивается, то график быстро приближается к оси Ох (не пересекая её). Таким образом, ось Ох является горизонтальной асимптотой графика.
Если х

Показательные уравнения

Рассмотрим несколько примеров показательных уравнений, т.е. уравнений, в которых неизвестное содержится в показателе степени. Решение показательных уравнений часто сводится к решению уравнения a x = a b где а > 0, \( a \neq 1\), х — неизвестное. Это уравнение решается с помощью свойства степени: степени с одинаковым основанием а > 0, \( a \neq 1\) равны тогда и только тогда, когда равны их показатели.

Решить уравнение 2 3x • 3 x = 576
Так как 2 3x = (2 3 ) x = 8 x , 576 = 24 2 , то уравнение можно записать в виде 8 x • 3 x = 24 2 , или в виде 24 x = 24 2 , откуда х = 2.
Ответ х = 2

Решить уравнение 3 х + 1 — 2 • 3 x — 2 = 25
Вынося в левой части за скобки общий множитель 3 х — 2 , получаем 3 х — 2 (3 3 — 2) = 25, 3 х — 2 • 25 = 25,
откуда 3 х — 2 = 1, x — 2 = 0, x = 2
Ответ х = 2

Решить уравнение 3 х = 7 х
Так как \( 7^x \neq 0 \) , то уравнение можно записать в виде \( \frac<3^x> <7^x>= 1 \), откуда \( \left( \frac<3> <7>\right) ^x = 1 \), х = 0
Ответ х = 0

Решить уравнение 9 х — 4 • 3 х — 45 = 0
Заменой 3 х = t данное уравнение сводится к квадратному уравнению t 2 — 4t — 45 = 0. Решая это уравнение, находим его корни: t₁ = 9, t₂ = -5, откуда 3 х = 9, 3 х = -5.
Уравнение 3 х = 9 имеет корень х = 2, а уравнение 3 х = -5 не имеет корней, так как показательная функция не может принимать отрицательные значения.
Ответ х = 2

Решить уравнение 3 • 2 х + 1 + 2 • 5 x — 2 = 5 х + 2 х — 2
Запишем уравнение в виде
3 • 2 х + 1 — 2 x — 2 = 5 х — 2 • 5 х — 2 , откуда
2 х — 2 (3 • 2 3 — 1) = 5 х — 2 ( 5 2 — 2 )
2 х — 2 • 23 = 5 х — 2 • 23
\( \left( \frac<2> <5>\right) ^ = 1 \)
x — 2 = 0
Ответ х = 2

Решить уравнение 3 |х — 1| = 3 |х + 3|
Так как 3 > 0, \( 3 \neq 1\), то исходное уравнение равносильно уравнению |x-1| = |x+3|
Возводя это уравнение в квадрат, получаем его следствие (х — 1) 2 = (х + 3) 2 , откуда
х 2 — 2х + 1 = х 2 + 6х + 9, 8x = -8, х = -1
Проверка показывает, что х = -1 — корень исходного уравнения.
Ответ х = -1

Решение уравнений онлайн

В общем виде, уравнение относительно некоторой переменной может быть записано следующим образом:

Решить, приведенное выше уравнение, означает найти все значения переменной при которых выражение обращается в верное тождество.

Графически, корни уравнения представляют собой абсциссы точек пересечения графика функции с осью :

Таким образом, из приведенного на рисунке графика некоторой функции , мы можем сразу сказать, что значения являются корнями уравнения .

В зависимости от конкретного вида функции существует бесконечное множество различных уравнений (линейные, квадратные, кубические, тригонометрические, уравнения с корнями, степенями и т.д.).

Наш онлайн калькулятор построен на основе системы Wolfram Alpha LLC и способен решить очень много различных типов уравнений с описанием подробного решения.

Контрольная работа по алгебре в 8 классе на тему «Дробно — рациональные уравнения»

Контрольная работа содержит 4 варианта с подробным решением.

Просмотр содержимого документа
«Контрольная работа по алгебре в 8 классе на тему «Дробно — рациональные уравнения»»

В а р и а н т 1

1. Решите уравнение:

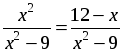
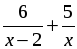
а) ; б) = 3.

2. Из пункта А в пункт В велосипедист проехал по одной дороге длиной 27 км, а обратно возвращался по другой дороге, которая была короче первой на 7 км. Хотя на обратном пути велосипедист уменьшил скорость на 3 км/ч, он все же на обратный путь затратил времени на 10 минут меньше, чем на путь из А в В. С какой скоростью ехал велосипедист из А в В?

В а р и а н т 2

1. Решите уравнение:

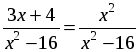
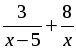
а) ; б) = 2.

2. Катер прошёл 12 км против течения реки и 5 км по течению. При этом он затратил столько времени, сколько ему потребовалось бы, если бы он шёл 18 км по озеру. Какова собственная скорость катера, если известно, что скорость течения реки равна 3 км/ч.

В а р и а н т 3

1. Решите уравнение:

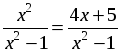
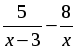
а) ; б) = 3.

2. Из пункта А в пункт В велосипедист проехал по дороге длиной 48 км, обратно он возвращался по другой дороге, которая короче первой на 8 км. Увеличив на обратном пути скорость на 4 км/ч, велосипедист затратил на 1 час меньше, чем на путь из А в В. С какой скоростью ехал велосипедист из пункта А в пункт В?

В а р и а н т 4

1. Решите уравнение:

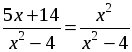
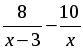
а) ; б) = 2.

2. Катер прошёл 15 км против течения и 6 км по течению, затратив на весь путь столько же времени, сколько ему потребовалось бы, если бы он шёл 22 км по озеру. Какова собственная скорость катера, если известно, что скорость течения реки равна 2 км/ч?

Решение вариантов контрольной работы

В а р и а н т 1

1. а) 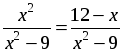. Общий знаменатель х 2 – 9.

По теореме, обратной теореме Виета, х₁ = 3; х₂ = –4.

Если х = 3, то х 2 – 9 = 0.

Если х = –4, то х 2 – 9 ≠ 0.

б) 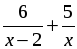= 3. Общий знаменатель х (х – 2).

D = (–17) 2 – 4 · 3 · 10 = 289 – 120 = 169, D 0, 2 корня.

x₁ = 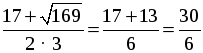= 5;

x₂ = .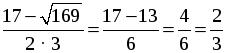

Если х = 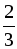, то х (х – 2) ≠ 0.

О т в е т: а) –4; б) 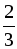; 5.

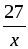
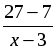
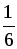
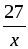
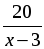
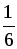
2. Пусть х км/ч – скорость велосипедиста, с которой он ехал из А в В, тогда (х – 3) км/ч – скорость, с которой он ехал обратно. На путь из А в В он затратил ч, а обратно ч. Зная, что на обратный путь он затратил на 10 мин ( часа) меньше, составим уравнение:

– = . Общий знаменатель 6х (х – 3).

D = (–45) 2 – 4 · 486 = 81, D 0, 2 корня.

x₁ = 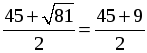= 27;

x₂ = 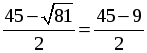= 18.

Ни один из корней не обращает знаменатель в нуль, но корень х = 27 не удовлетворяет условию задачи (слишком большая скорость для велосипедиста).

О т в е т: 18 км/ч.

В а р и а н т 2

1. а) 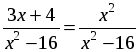. Общий знаменатель х 2 – 16.

По теореме, обратной теореме Виета х₁ = 4; х₂ = –1.

Если х = 4, то х 2 – 16 = 0.

Если х = – 1, то х 2 – 16 ≠ 0.

б) 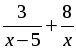= 2. Общий знаменатель х (х – 5).

D = (–21) 2 – 4 · 2 · 40 = 441 – 320 = 121, D 0, 2 корня.

x₁ = 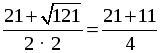= 8;

О т в е т: а) –1; б) 2,5; 8.

2. Пусть х км/ч – собственная скорость катера, тогда против течения он шёл со скоростью (х – 3) км/ч, по течению – (х + 3) км/ч и по озеру – х км/ч. Против течения он шёл ч, по течению ч, а по озеру он шёл бы ч. Зная, что на все плавание по реке он затратил бы столько же времени, сколько на плавание по озеру, составим уравнение:

12х 2 + 36х + 5х 2 – 15х – 18х 2 + 162 = 0;

D = (–21) 2 – 4 · 162 = 441 + 648 = 1089, D 0, 2 корня.

Ни один из корней не обращает знаменатель в нуль, но х = –6 не удовлетворяет условию задачи.

О т в е т: 27 км/ч.

В а р и а н т 3

1. а) 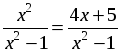. Общий знаменатель х 2 – 1.

По теореме, обратной теореме Виета, х₁ = 5; х₂ = –1.

Если х = 5, то х 2 – 1 ≠ 0.

Если х = –1, то х 2 – 1 = 0.

б) 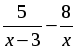= 3. Общий знаменатель х (х – 3).

По теореме, обратной теореме Виета, х₁ = 4; х₂ = –2.

О т в е т: а) 5; б) –2; 4.

2. Пусть х км/ч – скорость, с которой велосипедист ехал из А в В, тогда (х + 4) км/ч – скорость, с которой он ехал обратно. На путь из А в В он затратил ч, а обратно ч. Зная, что на обратный путь он затратил на 1 ч меньше, составим уравнение:

– = 1. Общий знаменатель х (х + 4).

Ни один из корней не обращает знаменатель в нуль, но корень х = –12 не удовлетворяет условию задачи.

О т в е т: 16 км/ч.

В а р и а н т 4

1. а) 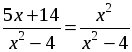. Общий знаменатель х 2 – 4.

По теореме, обратной теореме Виета, х₁ = 7; х₂ = –2.

Если х = 7, то х 2 – 4 ≠ 0.

Если х = –2, то х 2 – 4 = 0.

б) 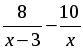= 2. Общий знаменатель х (х – 3).

По теореме, обратной теореме Виета, х₁ = 5; х₂ = –3.

О т в е т: а) 7; б) –3; 5.

2. Пусть х км/ч – собственная скорость катера, тогда против течения он шёл со скоростью (х – 2) км/ч, по течению – (х + 2) км/ч и по озеру – х км/ч. Против течения он шёл ч, по течению ч, а по озеру он шёл бы ч. Зная, что на все плавание по реке он затратил бы столько же времени, сколько на плавание по озеру, составим уравнение:

15х 2 + 30х + 6х 2 – 12х – 22х 2 + 88 = 0;

Ни один из корней не обращает знаменатель в нуль, но корень х = –4 не удовлетворяет условию задачи.