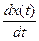Вариационное исчисление вывод уравнения эйлера

Вариационное исчисление вывод уравнения эйлера

Пример 2.1. Рассмотрим пример, который легко решить аналитически. Требуется найти экстремум функционала

при граничных условиях

Найдём частные производные и

Вычислим полную производную по x от

Составляем дифференциальное уравнение Эйлера вида

или, после упрощений

Его общее решение имеет вид

Для нахождения произвольных постоянных C₁ и C₂ подставим решение (2.16) в граничные условия (2.11):

Видно, что система (2.17) имеет единственное решение. Решая эту систему, найдём значения C₁ и C₂:

и тогда уравнение экстремали имеет вид:

Действительно ли на этой кривой достигается экстремум? И если да, то какой: минимум или максимум? Далее, в главе 13, мы рассмотрим достаточные условия экстремума . В частности, мы выведем условие Лежандра: если на экстремали выполняется условие а на функциях, близких к экстремали, для произвольных y‘ имеет место то достигается сильный минимум. В нашем случае это выполняется:

и, следовательно, на нашей экстремали достигается сильный минимум. Проверим этот результат: вычислим на нескольких функциях вида Эти функции удовлетворяют граничным условиям (2.11) и, следовательно, являются допустимыми. Для вычислений применим MATLAB.

Действительно, полученный результат не противоречит выводу о том, что на функции достигается минимум. Но, конечно же, проведенная проверка не доказывает этот факт. Ведь мы проверили только несколько из бесконечного числа функций, графики которых проходят через точки и Доказательством могут служить необходимые и достаточные условия экстремума функционала.

Пример 2.2. Найти экстремаль функционала

при граничных условиях

Выводим уравнение Эйлера вида (2.9). Частные производные:

Уравнение Эйлера после упрощений имеет вид:

Его общее решение

Находим произвольные постоянные из граничных условий (3.22). Подставляем решение (3.25) в эти граничные условия:

Мы видим, что из полученной системы уравнений можно найти только а C₂ может быть произвольной. Поэтому данная вариационная задача имеет бесчисленное множество решений вида

На любой из этих функций функционал принимает постоянное значение (какое − мы сейчас посчитаем). Проверка по достаточному условию Лежандра даёт:

поэтому на экстремалях (3.27) достигается сильный минимум.

Посчитаем значение функционала (2.21) на функциях вида (2.27) и нарисуем несколько экстремалей с помощью MATLAB.

На каждой из наших функций функционал равен нулю.

2.2. Частные случаи уравнений Эйлера

Иногда решение уравнения Эйлера существенно упрощается. Рассмотрим соответствующие частные случаи.

2.2.1. Подынтегральная функция F не зависит явно от y‘

Материал этого подраздела изложен в книге.

2.2.2. Подынтегральная функция F линейно зависит от y‘

Материал этого подраздела изложен в книге.

2.2.3. Подынтегральная функция F не зависит явно от y

Материал этого подраздела изложен в книге.

2.2.4. Подынтегральная функция F зависит только от y‘

Материал этого подраздела изложен в книге.

2.2.5. Подынтегральная функция F не зависит явно от x

Материал этого подраздела изложен в книге.

2.3. Вопросы для самопроверки

1. Какую вариационную задачу мы решаем?
2. Как выводится дифференциальное уравнение Эйлера?
3. Где используется в выводе дифференциального уравнения Эйлера основная лемма вариационного исчисления?
4. Почему обращается в нуль внеинтегральное слагаемое в формуле (2.8) при интегрировании по частям?
5. Чем отличается частная производная от полной?
6. Какие Вы знаете методы решения дифференциальных уравнений порядка?
7. Всегда ли решение вариационной задачи будет единственным? От чего это зависит?
8. Какие частные случаи уравнения Эйлера Вы знаете?
9. В каких случаях уравнение Эйлера перестаёт быть дифференциальным и становится конечным?
10. В каких случаях вариационная задача теряет смысл?
11. Как записывается интеграл уравнения Эйлера, если подынтегральная функция F не зависит явно от y?
12. Каким будет решение уравнения Эйлера, если подынтегральная функция F зависит только от y‘?
13. Как решается уравнение Эйлера, если подынтегральная функция F не зависит явно от y‘?
14. Как решается задача о брахистохроне?

2.4. Примеры выполнения заданий

2.4.1. Задание 1

Найти экстремаль функционала

Исследовать полученную экстремаль на достаточные условия экстремума. Вычислить значение функционала на найденной экстремали и, для сравнения, на прямой, соединяющей точки и Построить график решения.

В этом примере подынтегральная функция является функцией общего вида, поэтому составим уравнение Эйлера в виде (2.9) и решим его. Затем построим график решения. Попутно исследуем на выполнение достаточных условий экстремума и вычислим значение функционала на экстремали и отрезке прямой M₁M₂. Применим для решения задачи MATLAB.

Очистим память. Напечатаем заголовок решаемой задачи. Если хотите, задайте другую строку для вывода (например, свою фамилию). Опишем символические переменные [58]. Для решения уравнения Эйлера используем принятые в MATLAB обозначения производных: Dy для y‘ и D2y для y». Аргумент обозначим x , а функцию − y .

Вводим подынтегральную функцию и граничные условия. Печатаем их. Здесь вы должны поставить свои исходные данные: подынтегральную функцию F и граничные условия x₁, y₁, x₂, y₂.

Начинаем вывод дифференциального уравнения Эйлера (2.9). Найдём частные производные F_y и F_y’. Напечатаем их.

В уравнение Эйлера (2.9) входит полная производная Вычислим её по обычной формуле дифференцирования сложной функции:

Напечатаем её. Напечатаем также величину необходимую для проверки достаточных условий экстремума по признаку Лежандра.

Составим левую часть дифференциального уравнения Эйлера (2.9) и упростим её. Преобразуем символическую переменную Euler в строку.

Мы составили уравнение Эйлера, теперь решим его. Команда dsolve позволяет находить как общее решение дифференциального уравнения, так и частное его решение, удовлетворяющее заданным начальным или граничным условиям. В следующих главах при решении других заданий нам нужно будет иметь общее решение уравнения Эйлера. Найдём его.

Сформируем теперь уравнения для граничных условий. Подставим в найденное аналитическое решение Sol граничные точки x1 и x2 , и приравняем их соответственно y1 и y2 .

Решаем полученную систему конечных уравнений − находим значения произвольных постоянных C1 и C2 . Присваиваем найденные решения символическим константам, полученным при решении дифференциального уравнения. Теперь вычисляем аналитическое решение Sol21 . Такое вычисление сводится к тому, что в него будут подставлены найденные значения констант C1 и C2 . Печатаем найденное уравнение экстремали.

Вычислим значения функционала (2.86) на найденной экстремали и на прямой, соединяющей точки M₁ и M₂. Подставим в подынтегральную функцию F аналитические выражения для этих линий и их производных, а затем проинтегрируем. Напечатаем результаты.

В данном примере условие Лежандра говорит о сильном минимуме, что подтверждается полученным результатом: значение функционала на экстремали меньше, чем на другой допустимой функции. А как в вашем варианте: какой экстремум достигается? И подтверждается ли этот результат сравнением величин Jextr и Jlin ? Если нет, то не забудьте, что найденный экстремум − только локальный, а не глобальный! Попробуйте вычислить значение функционала не на прямой M₁M₂, а на какой-нибудь другой допустимой кривой, достаточно близкой к экстремали. Например, можно наложить на экстремаль несколько полуволн синусоиды, смещённой и деформированной вдоль оси Ox так, что

И, наконец, строим график. Задаём массив аргументов для рисования графика функции и вычисляем значения функции. Рисуем график, подписываем заголовок и координатные оси установленным шрифтом.

2.4.2. Задание 2

Найти экстремаль функционала

Исследовать на выполнение достаточных условий экстремума. Построить график решения.

В этом примере подынтегральная функция не зависит явно от y. Первый интеграл уравнения Эйлера имеет вид (2.43). Составим программу для решения этой вариационной задачи. Вначале введём исходные данные. У нас будет первый интеграл уравнения Эйлера, поэтому ни сама функция y, ни её вторая производная y» нам не нужны, и мы их не описываем. Поставьте свою подынтегральную функцию и граничные условия.

Строим первый интеграл и решаем полученное дифференциальное уравнение. Названия констант C1 и C2 используются в команде dsolve , поэтому при составлении интеграла уравнения Эйлера обозначим константу C . Все использованные здесь функции и операторы MATLAB были описаны ранее, в примере 1.

В переменной Sol получено общее решение, произвольные постоянные обозначены C и C1 . Найдём их. Для этого подставим в Sol граничные точки. Приравняем полученные выражения соответственно y1 и y2 . Тем самым мы сформируем систему уравнений.

Решим полученную систему − найдём произвольные постоянные C и C1 . Подставим их в решение Sol . Ограничим решение 14 знаками. Напечатаем уравнение найденной экстремали.

Дальнейшие действия не отличаются от описанных в примере 1. Рисуем график и и вычисляем F_y’y’, которая нужна для проверки достаточных условий экстремума по признаку Лежандра.

Проанализируйте достаточное условие Лежандра. Достигается ли экстремум на вашей экстремали? Если да, то какой?

2.4.3. Задание 3

Решить задачу о брахистохроне, соединяющей точки и

Мы уже решили эту задачу аналитически. Нам осталось найти значение константы C₁ и параметра в конечной точке t₂ из решения системы уравнений (2.84). Составим программу для решения этого примера. Вначале введём исходные данные задачи. Подставьте свою правую точку.

Составляем систему уравнений (2.84). Левую часть каждого уравнения мы задаём сразу в виде строки. В правой части переводим числа x2 и y2 в их строковые представления с помощью функции num2str . Ранее мы использовали конструкцию char(sym(y2)) . Оба варианта работают правильно − вы можете это проверить. Решаем полученную систему уравнений аналитически. Печатаем решения.

Рисуем график полученной брахистохроны. Выбираем начало координат в левом верхнем углу с помощью команды axis . Задаём границы по оси Ox, чтобы график занимал всё место на рисунке. Выравниваем масштабы по осям координат, чтобы брахистохрона выглядела неискажённой. Надписываем заголовок и метки осей.

2.5. Задание

Для своего варианта функционалов 1, 2, 3 найти экстремали, построить их графики и исследовать на выполнение достаточных условий экстремума.

Формировка простейшей вариационной задачи классического вариационного исчисления. Вывод уравнение Эйлера.

Основные понятия вариационного исчисления: функционал, непрерывный функционал, линейный функционал, вариация функционала.

Задача синтеза оптимальных систем в конечном счете сводится к отысканию вектора U(t) управления, обеспечивающего экстремальное (т. е. минимальное или максимальное) значение некоторого критерия качества – некоторого функционала. Как известно, методы отыскание экстремальных значений функционалов составляют основу вариационного исчисления.

1.Переменная величина V называется функционалом, зависящим от функции x(t) V = V[x(t)], если каждой функции из некоторого класса соответствует значение V, т. е. функции x(t) соответствует число V.

Пример 1: .

Набору функций e — t / T 1 , e — t / T ₂ , …, e — t / T _n будут соответствовать числа , …, _.

Пример2: функционал зависит не только от функции , но и ее производной x(t). Известно, что длина кривой x(t) сое диняющей на плоскости x, t точки t=0, x=0 и t=1,x=1 будет равна интегралу ; x ’ (t)=

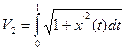
2.Приращением или вариацией x аргумента x(t) функционала V[x(t)] называется разность между двумя функциями , причем x(t), x₁(t) .

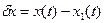
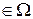
3. Функционал V[x(t)] называется непрерывным, если малому изменению x(t) cоответствует малое изменение функционала V[x(t)].

3a) Функционал V[x(t)] непрерывен при x₀(t) в смысле близости k-го порядка, ес ли для любого можно подобрать такое , что |V[x(t)-V[x₀(t)]| при , ,- — — — — — — .

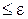
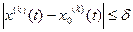
4. Линейным функционалом называется функционал L[x(t)], удовлетворяющий условиям: L[C*x(t)] =C*L[x(t)], где С — произвольная постоянная, и L[x₁(t)+x₂(t)]=L[x₁(t)]+L[x₂(t)]

Примером является

5. Если приращение функционала DV = V[x(t)+dx]-V[x(t)] можно представить в виде DV=L[x(t),dx]+B(x(t),dx)*r(x+dx,x), где L[x(t),dx] – линейный по отношению к dx функционал, и B(x(t),dx)®0 при r(x+dx,x)®0, то линейная по отношению dx часть приращения функционала, т.е. L[x(t),dx], называется вариацией функционала и обозначается dV.

6. Теорема. Если функционал V[x(t)], имеющий вариацию, достигает минимума при x₀(t), где x₀(t) – внутренняя точка области определения функционала, то dV = 0.

Если dV¹0, то при достаточно малом расстоянии r(x+dx,x) знак правой части совпадает со знаком dV, но dV меняет знак при изменении знака dx вследствие линейности, следовательно, при достаточно малом r(x+dx,x) и знак DV изменяется при изменении знака dx, т.е. при x₀(t) не достигается ни макс, ни мин. Т.о., необходимым условием экстремума функционала явл. dV=0.

Основные понятия вариационного исчисления: функционал, сильный и слабый экстремум функционала, условия экстремума.

Переменная величина V называется функционалом, зависящим от функции x(t) V = V[x(t)], если каждой функции из некоторого класса соответствует значение V, т. е. функции x(t) соответствует число V.Пример: ; Набору функций e — t / T 1 , e — t / T ₂ , …, e — t / T _n будут соответствовать числа , …, _.

Функции, обеспечивающие экстремум функционала, называются экстремалями.

По определению функционал V[x(t)] достигает на кривой x₀(t) минимума, если его значение на любой, достаточно близкой к х₀(t) кривой не меньше, чем V[x₀(t)], т.е. DV = V[x(t)] — V[x₀(t)] = 0. Говоря о максимуме или минимуме функционала, мы подразумеваем наибольшее или наименьшее значение функционала по отношению к его значениям на близких кривых, но близость кривых может быть понимаема различно. Так например, если значение функционала на некоторой кривой меньше, чем на всех других допустимых кривых, близких в смысле близости нулевого порядка, то говорят, что на этой кривой достигается сильный минимум.

Если же на кривой х₀(t) достигается минимум по отношению к более узкому классу (множеству) кривых, для которых не только модуль разности мал, но мал также и , т.е. имеет место близость первого порядка, то минимум называется слабым.

Подчеркнем, что сильный минимум является одновременно и слабым, но не наоборот. Необходимо отметить, что в сформулированной простейшей задаче вариационного исчисления определяется слабый минимум. И вообще для классического вариационного исчисления характерно в основном исследование задач на слабый экстремум функционалов. Условия сильного экстремума устанавливает принцип максимума Л.С. Понтрягина.

Если приращение функционала DV = V[x(t)+dx]-V[x(t)] можно представить в виде DV=L[x(t),dx]+B(x(t),dx)*r(x+dx,x), где L[x(t),dx] – линейный по отношению к dx функционал, и B(x(t),dx)®0 при r(x+dx,x)®0, то линейная по отношению dx часть приращения функционала, т.е. L[x(t),dx], называется вариацией функционала и обозначается dV.

Теорема. Если функционал V[x(t)], имеющий вариацию, достигает минимума при x₀(t), где x₀(t) – внутренняя точка области определения функционала, то dV = 0.

Если dV¹0, то при достаточно малом расстоянии r(x+dx,x) знак правой части совпадает со знаком dV, но dV меняет знак при изменении знака dx вследствие линейности, следовательно, при достаточно малом r(x+dx,x) и знак DV изменяется при изменении знака dx, т.е. при x₀(t) не достигается ни максимум, ни минимум. Таким образом, необходимым условием экстремума функционала является dV=0.

Введенное понятие вариации функционала, как главной линейной части приращения, известное также как сильного дифференциала (диф. Фреше) функционала, относительно сложно вычислить. В связи с этим появилось понятие слабого дифференциала (дифференциала Гато) , где функция a*h(t) есть вариация аргумента x(t) и принадлежит тому же классу функций, что и x(t); a — параметр.Доказана теорема, что если существует сильный дифференциал функционала, то существует и слабый дифференциал (но не наоборот), причем в этом случае дифференциалы совпадают.

Уравнение Эйлера – Пуассона

Простейшую вариационную задачу можно обобщить на случай, когда подынтегральная функция содержит производные высших порядков и функционал имеет вид

. (1)

Здесь функция F предлагает (n+2) раза дифференцируемой по всем аргументам, а граничные условия заданы в форме

(2)

т.е. в граничных точках заданы значения не только функции, но и ее производных до порядка (n-1) включительно (всего 2n условий).

Решение задачи J = min ищется в классе C_2n[t₀,t₁] гладких 2n раз дифференцируемых функций. Методика получения необходимого условия минимума функционала остается прежней: находится первая вариация критерия и приравнивается к нулю, что после преобразований приводит к уравнению

, (3)

которые называются уравнением Эйлера-Пуассона и представляет в общем случае нелинейное дифференциальное уравнение 2n-порядка.

Его решение x(t,c₁,c₂,…,c_2n) содержит 2n постоянных интегрирования. Последние находятся на основании такого же количества граничных условий (2).

Дадим вывод уравнения (3), ограничившись для простоты выкладок случаем, когда функционал зависит от производной не старше второго порядка:

. (4)

Предположим, что экстремум достигается на функции x(t), и прибавим к ней вариацию такую, что на концах при t=t₀ и t=t₁ как обращаются в нуль.

Определим вариацию функционала

. (5)

Преобразуем теперь выражение (5), пользуясь формулой интегрирования по частям, причем третий член вариации будем интегрировать по частям дважды:

(6)

. (7)

Вследствие условий на концах участка все неинтегральные члены обращаются в нуль, и, следовательно, на основе (5) — (7) получаем

. (8)

Поскольку необходимым условием экстремума является равенство нулю первой вариации функционала, а вариация произвольна, то из равенства и леммы Лагранжа (основной леммы вариационного исчисления) следует уравнение (3).

В этом случае имеет место следующий аналог условия Лагранжа, позволяющий отличить максимум от минимума функционала (1): если функция x(t) доставляет минимум (максимум) функционалу, необходимо, чтобы ).

ОТВЕТЫ ПО НЕКЛАССИЧЕСКОМУ ВАРИАЦИОННОМУ ИСЧИСЛЕНИЮ

ВОПРОСЫ ПО ТЕОРИИ АКОР

Основные понятия адаптивного управления. Адаптивная система со стабилизацией частотной характеристики разомкнутого объекта.

Общие понятия об адаптивном управлении.Для математической формулировки и последующего решения задачи синтеза оптимальной системы уравнения необходимо располагать определенными сведениями об объекте управления в условиях работы системы. Объект управления должен быть ма­тематически описан, т.е. найдено его дифференциальное уравнение или какой-нибудь аналог уравнения. Также должно быть детерминированном или вероятном смысле известны свойства задающих и возмущающих воздействий. Наличие такой априорной информации позволяет синтезировать оптимальную и неоптимальную систему, но имеющую нужные показатели качества. Во многих реальных ситуациях информация о свойствах объекта управления и внешних воздействиях оказывается недостаточной для построения системы с необходимыми показателями качества.

Эта недостаточность может носить двоякий характер. В первом случае на этапе проектирования структуры и расчета параметров. УУ или некоторой его части могут оказаться полностью или частично не известными свойствами ОУ и внешних воздействий. Сис­тема управления в процессе функционирования сама должна автоматически восполнять недостающую информацию и по мере ее поступления изменять структуру и параметры УУ так, чтобы показатель качества или достигал экстремального значения, или соответствовал заданным огра­ничениям. После восстановления всей недостающей информацией при У неизменных в последующем свойствах ОУ и внешних воздействиях процесс изменения структуры и параметров УУ прекращается и система работает в обычном режиме.

Во втором случае имеются исходные сведения о свойствах ОУ и внешних воздействий, позволяющих синтезировать УУ. Однако в процессе работы системы эти свойства в силу различных причин мо­гут изменяться, поэтому заранее достоверно прогнозировать характер изменения не удается. Эти изменения, если они происходят в доста­точно большом диапазоне, могут привести к тому, что УУ, спроектированное в ориентации на некоторую начальную информацию, в новых условиях уже не обеспечит соответствие показателя качества существующим ограничениям. Качество может оказаться не экстремальным, т.е. в новых условиях система не будет оптимальной, или выйдет из требуемого диапазона.

Две перечисленные ситуации изменения свойств ОУ и внешних воздействий не исключают возможнос­ти существования третьей, в которой необходимая для синтеза УУ информация может быть как неизвестна на начальном этапе так и подвер­гаться непрогнозируемым изменениям в последующем. Однако незави­симо от конкретизации ситуации общим для всех отмеченных случаев является то, что система управления в процессе функционирования должна реагировать на изменение свойств ОУ и внешних воздействий и на основании результатов обработки соответствующей информации приспосабливаться к новым условиям путем изменения структуры и параметров УУ или некоторой его части так, чтобы показатель ка­чества каждый раз достигал экстремального значения или находился в заданном диапазоне. Такие системы автоматического управления принято называть адаптивными, а процесс изменения структуры и па­раметров УУ, осуществляемый на основании информации о свойствах ОУ и внешних воздействий и обеспечивающий приспосабливаемость системы к изменяющимся условиям работы, адаптацией. Если адаптация обусловлена только отсутствием начальной ин­формации о свойствах ОУ и внешних воздействий и после ее воспол­нении из-за неизменности этих свойств необходимое качество управления обеспечивается при неизменных структуре и параметрах УУ, адаптацию принято называть однократное. В остальных случаях коррекция управляющего устройства осуществляется каждый раз при изменении свойств ОУ или внешних воздействий и адаптация называ­ется многократной.

СНС со стабилизацией амплитудно-частотных характеристик.При построении систем управления очень важно иметь возмож­ность поддерживать свойства замкнутой системы неизменными в ши­роком диапазоне изменения свойств ОУ. Свойства линейной замкнутой системы удобно оценивать по виду ее амплитудно-частотных характеристик или импульсной характеристики. Соответствующие системы, если эффект стабилизации обеспечивается рациональным из­менением параметров УУ на основании получаемой в процессе рабо­ты системы информации об ОУ принято относить к СНС со стабилиза­цией качества управления. Характерным для таких систем является наличие модели, отражающей желаемые свойства замкнутой или разомкнутой системы.

Пусть проектируется система управления минимально фазовым ОУ, особенность которых состоит в возможности исследования их частотных свойств только по виду АЧХ.

Предусмотрим в структуре УУ корректирующие цепи с переменными параметрами, изменяющимися в процессе работы системы при изменении свойств ОУ. Число m таких параметров целесообразно выбрать рав­ным числу переменных параметров в уравнении ОУ, хотя из соображе­ний простоты технической реализуемости число m может быть умень­шено. Параметры корректирующих цепей следует изменять так, чтобы свойства проектируемой системы были тождественны свойствам модели при всех состояний ОУ. Для этого можно на m частотах измерить АЧХ разомкнутой системы и полученные результаты сравнить с аналогичными значениями модели. На основании результатов сопоставления изменяются параметры УУ в направлении устранения рассогласования. Схема реализации такого исхода изображена на рис. 1.

Основной контур включает в себя объект управления, характе­ризующийся медленно изменяющимися в системе параметрами. Эта «мед­ленность» позволяет СУ вместе с неизменной частью УУ на интервалах времени, соизмеримых с длительностью переходных процессов, харак­теризовать передаточной функцией W0(p). В основной контур вхо­дит и корректирующее устройство, состоящее из m параллельно соединенных цепей с переменными коэффициентами ai (положит, сигналы с выходов интеграторов, подаваемые на умножители) и фильтрами Wi(p), . Выбор функций Wi(p) и диапазон изменения коэффициентов ai должны быть подчинены следующему достигаемому во всей области изменения параметров ОУ условию: (1) в котором левая часть представляет собой передаточную функций разомкнутой проектируемой системы. [WM(p)] — передаточная функ­ция модели. Условие (1) считается приближенно достигнутым, если выпол. равенство (2) т.е. у проектируемой системы АЧХ совпадает с АЧХ модели на m частотах . Последние должны равномерно покрывать всю полосу пропускания модели. Чтобы (2) заведомо имели действи­тельные решения относительно ai, в качестве фильтров Wi(p) выбирают узкополосные устройства, обладающие свойствами при , тогда из (2)следует (3)

Для выбора только положительных величин коэффициентов, что обеспечивает, однозначность решения (3) схемой предусмотрена система детекторов Д, которые пропускают лишь положительные входные сигналы и образуют на выходах нули при отрицательных входных сигналах. На вход системы для контроля за частотными свойствами помимо основного подается пробный сигнал , содержащий весь спектр частот .

Сигнал рассогласования подается на вход модели. Сиг­налы с выходов модели и системы преобразуются m узкополосными резонансными фильтрами с передаточными функциями , , настроенными на рабочие частоты , т.е. из всего спектра входных сигналов — пропускающими частоты» близкие к . Сигналы с выходов фильтров выпрямляются детекторами, так что для установившегося режима можем записать , (4) , (5) где амплитуда — гармоники спектра сигнала .

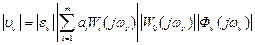
Сигналы (4) и (5) попарно вычитаются и подаются на входы ин­тегралов с пер. функ. 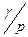. Положительные сигналы с выходов интеграторов пропускаются детекторами представляют собой значения коэффициентов настройки корректирующих цепей, которые при условии подчинены уравнениям. . Последнее уравнение можно переписать в диф. форме ; , что с учетом (4) и (5) можно представить в виде

(6) где , .

Соотношения (6)являются уравнениями контура самонастройки и показывают, что при изменении свойств ОУ величины должны меняться до тех пор, пока не бу­дут выполнены условия совпадения (2) АЧХ проектируемой системы и модели. Если выполняется условие при уравнения (6) становятся независимыми, так что , (7) Этим уравнением первого порядка соответствуют всегда устой­чивые процессы, поэтому при любых начальных значениях коэффициен­тов в последующем установятся такие значения, при которых бу­дет достигнут результат самонастройки (2), т.е. независимо от изменения свойств ОУ свойства всей системы будут соответствовать модели.

Основные понятия вариационного исчисления: функционал, непрерывный функционал, линейный функционал, вариация функционала.

Задача синтеза оптимальных систем в конечном счете сводится к отысканию вектора U(t) управления, обеспечивающего экстремальное (т. е. минимальное или максимальное) значение некоторого критерия качества – некоторого функционала. Как известно, методы отыскание экстремальных значений функционалов составляют основу вариационного исчисления.

1.Переменная величина V называется функционалом, зависящим от функции x(t) V = V[x(t)], если каждой функции из некоторого класса соответствует значение V, т. е. функции x(t) соответствует число V.

Пример 1: .

Набору функций e — t / T 1 , e — t / T ₂ , …, e — t / T _n будут соответствовать числа , …, _.

Пример2: функционал зависит не только от функции , но и ее производной x(t). Известно, что длина кривой x(t) сое диняющей на плоскости x, t точки t=0, x=0 и t=1,x=1 будет равна интегралу ; x ’ (t)=

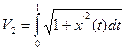
2.Приращением или вариацией x аргумента x(t) функционала V[x(t)] называется разность между двумя функциями , причем x(t), x₁(t) .

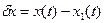
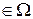
3. Функционал V[x(t)] называется непрерывным, если малому изменению x(t) cоответствует малое изменение функционала V[x(t)].

3a) Функционал V[x(t)] непрерывен при x₀(t) в смысле близости k-го порядка, ес ли для любого можно подобрать такое , что |V[x(t)-V[x₀(t)]| при , ,- — — — — — — .

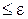
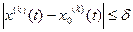
4. Линейным функционалом называется функционал L[x(t)], удовлетворяющий условиям: L[C*x(t)] =C*L[x(t)], где С — произвольная постоянная, и L[x₁(t)+x₂(t)]=L[x₁(t)]+L[x₂(t)]

Примером является

5. Если приращение функционала DV = V[x(t)+dx]-V[x(t)] можно представить в виде DV=L[x(t),dx]+B(x(t),dx)*r(x+dx,x), где L[x(t),dx] – линейный по отношению к dx функционал, и B(x(t),dx)®0 при r(x+dx,x)®0, то линейная по отношению dx часть приращения функционала, т.е. L[x(t),dx], называется вариацией функционала и обозначается dV.

6. Теорема. Если функционал V[x(t)], имеющий вариацию, достигает минимума при x₀(t), где x₀(t) – внутренняя точка области определения функционала, то dV = 0.

Если dV¹0, то при достаточно малом расстоянии r(x+dx,x) знак правой части совпадает со знаком dV, но dV меняет знак при изменении знака dx вследствие линейности, следовательно, при достаточно малом r(x+dx,x) и знак DV изменяется при изменении знака dx, т.е. при x₀(t) не достигается ни макс, ни мин. Т.о., необходимым условием экстремума функционала явл. dV=0.

Основные понятия вариационного исчисления: функционал, сильный и слабый экстремум функционала, условия экстремума.

Переменная величина V называется функционалом, зависящим от функции x(t) V = V[x(t)], если каждой функции из некоторого класса соответствует значение V, т. е. функции x(t) соответствует число V.Пример: ; Набору функций e — t / T 1 , e — t / T ₂ , …, e — t / T _n будут соответствовать числа , …, _.

Функции, обеспечивающие экстремум функционала, называются экстремалями.

По определению функционал V[x(t)] достигает на кривой x₀(t) минимума, если его значение на любой, достаточно близкой к х₀(t) кривой не меньше, чем V[x₀(t)], т.е. DV = V[x(t)] — V[x₀(t)] = 0. Говоря о максимуме или минимуме функционала, мы подразумеваем наибольшее или наименьшее значение функционала по отношению к его значениям на близких кривых, но близость кривых может быть понимаема различно. Так например, если значение функционала на некоторой кривой меньше, чем на всех других допустимых кривых, близких в смысле близости нулевого порядка, то говорят, что на этой кривой достигается сильный минимум.

Если же на кривой х₀(t) достигается минимум по отношению к более узкому классу (множеству) кривых, для которых не только модуль разности мал, но мал также и , т.е. имеет место близость первого порядка, то минимум называется слабым.

Подчеркнем, что сильный минимум является одновременно и слабым, но не наоборот. Необходимо отметить, что в сформулированной простейшей задаче вариационного исчисления определяется слабый минимум. И вообще для классического вариационного исчисления характерно в основном исследование задач на слабый экстремум функционалов. Условия сильного экстремума устанавливает принцип максимума Л.С. Понтрягина.

Если приращение функционала DV = V[x(t)+dx]-V[x(t)] можно представить в виде DV=L[x(t),dx]+B(x(t),dx)*r(x+dx,x), где L[x(t),dx] – линейный по отношению к dx функционал, и B(x(t),dx)®0 при r(x+dx,x)®0, то линейная по отношению dx часть приращения функционала, т.е. L[x(t),dx], называется вариацией функционала и обозначается dV.

Теорема. Если функционал V[x(t)], имеющий вариацию, достигает минимума при x₀(t), где x₀(t) – внутренняя точка области определения функционала, то dV = 0.

Если dV¹0, то при достаточно малом расстоянии r(x+dx,x) знак правой части совпадает со знаком dV, но dV меняет знак при изменении знака dx вследствие линейности, следовательно, при достаточно малом r(x+dx,x) и знак DV изменяется при изменении знака dx, т.е. при x₀(t) не достигается ни максимум, ни минимум. Таким образом, необходимым условием экстремума функционала является dV=0.

Введенное понятие вариации функционала, как главной линейной части приращения, известное также как сильного дифференциала (диф. Фреше) функционала, относительно сложно вычислить. В связи с этим появилось понятие слабого дифференциала (дифференциала Гато) , где функция a*h(t) есть вариация аргумента x(t) и принадлежит тому же классу функций, что и x(t); a — параметр.Доказана теорема, что если существует сильный дифференциал функционала, то существует и слабый дифференциал (но не наоборот), причем в этом случае дифференциалы совпадают.

Формировка простейшей вариационной задачи классического вариационного исчисления. Вывод уравнение Эйлера.