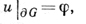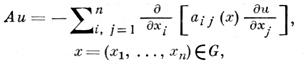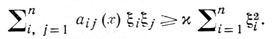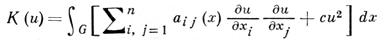Вариационные методы решения уравнений с частными производными

ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ; вариационные методы решения

ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ; вариационные методы решения — методы решения краевых задач для Д. у. с ч. п. при помощи сведения этих задач (когда это возможно) к соответствующим образом подобранным вариационным задачам (т. е. к задачам на отыскание минимума или максимума нек-рого функционала) и решения последних.

Вариационные методы широко применяются как в теоретич. исследованиях (для доказательства теорем существования, единственности и устойчивости решений, при исследовании дифференциальных свойств решений, в спектральной теории, при изучении разнообразных вопросов оптимизации и т. д.), так и в вопросах, связанных с нахождением приближенных решений уравнений. Приближенные решения вариационных задач можно находить при помощи решения конечных систем алгебраич. уравнений, при этом алгоритмы нахождения приближенных решений вариационных задач часто оказываются проще и удобнее, чем имеющиеся алгоритмы решения соответствующих задач для Д. у. с ч. п.

Вариационный метод исследования краевых задач возник в сер. 19 в. в виде так наз. Дирихле принципа отыскания в области G гармония, функции, принимающей на границе ∂G области G данное значение φ(х), x ∈ ∂G, как функции, дающей в рассматриваемом классе функций минимум интегралу Дирихле. Первоначально принцип Дирихле применялся лишь в теории линейных эллиптич. уравнений 2-го порядка (впоследствии и более высоких порядков), а затем и в теории уравнений других типов, причем не только линейных, но и нелинейных. Разработке вариационных методов были посвящены работы Б. Римана (В. Riemann), К. Вейерштрасса (К. Weierstrass), Д. Гильберта (D. Hilbert). Большую роль в развитии вариационных методов, в частности в вопросе их обоснования, сыграли вложения теоремы и их обобщения.

Одним из простых и типичных примеров использования вариационных методов является решение Дирихле задачи для эллиптического самосопряженного уравнения 2-го порядка

(G — область конечномерного евклидова пространства, ∂G — ее граница, φ — заданная на ∂G функция), и существует постоянная ϰ > 0 такая, что для всех точек x ∈ G и всех чисел ξ₁ ξ₂, . ξ_n выполняется неравенство (условие эллиптичности)

В этом случае вариационный метод решения задачи (1) — (2) состоит в отыскании функции u(х), для к-рой функционал

(уравнение (1) является Эйлера уравнением для функционала К(u)) принимает наименьшее значение в классе допустимых функций, т. е. таких функций u(х), для к-рых A(u)

Аналитические методы решения уравнений в частных производных

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

К курсовой работе по дисциплине

«ЧИСЛЕННЫЕ МЕТОДЫ»

Рецензент – доцент В.В. Луценко

Составитель Бондаренко А.И.

Методические указания к курсовой работе по дисциплине «Численные методы»/ Сост. А.И. Бондаренко; Шахтинский ин-т (филиал) ЮРГТУ (НПИ). – Новочеркасск: ЮРГТУ, 2008. — 12 с.

Методические указания содержат теоретический материал, примеры выполнения и требования к оформлению курсовой работы по дисциплине «Численные методы».

Предназначены для студентов второго курса специальностей 230201«Информационные системы и технологии» и 0808001 «Прикладная информатика».

© Шахтинский институт ЮРГТУ, 2008

© Бондаренко А.И., 2008

ВВЕДЕНИЕ

Изучение различных процессов требует наряду с глубоким пониманием физики происходящих явлений совершенного владения современными методами вычислительной математики.

Обычно математическая модель записывается в форме как угодно сложных математических структур и, как правило, получить аналитическое решение такой задачи не удаётся. Приходится использовать численные методы вычислительной математики, реализация которых на ЭВМ требует соответствующего программного обеспечения. Результаты моделирования объекта на ЭВМ позволяют “проиграть” его поведение в самых разных, под­час экстремальных условиях. Значение такого вычислительного экспери­мента трудно переоценить, особенно если натурный эксперимент опасен, дорог или просто невозможен.

Большинство физических процессов можно сформулировать на языке дифференциальных уравнений с частными производными. Производные в этих уравнениях описывают важнейшие физические величины: скорость, ускорение, силу, температуру, трение, ток, потенциал и т.д.). Многие из таких уравнений не имеют аналитического решения и, чтобы их решить, приходится прибегать к численным методам.

В курсовой работе рассматривается одно из самых важных уравнений математической физики — уравнение Лапласа на примере решения задачи Дирихле в заданной плоской области. Отсутствие аналитического решения поставленной задачи требует выбора численного метода и его реализации на ЭВМ.

Курсовая работа является завершающим этапом изучения курса “Численные методы”. Цель курсовой работы:

· систематизация, закрепление и расширение теоретических и практических знаний по компьютерному моделированию типовых вычислительных алгоритмов и анализа полученной информации;

· выявление степени подготовленности студентов к самостоятельной работе в ходе решения поставленных задач.

Аналитические методы решения уравнений в частных производных

Существует целый арсенал методов для решения уравнений в частных производных. Перечислим некоторые аналитические методы решения таких уравнений.

Метод разделения переменных. Уравнение с частными производными с n независимыми переменными сводится к n обыкновенным дифференциальным уравнениям. Решение краевых задач для уравнения Лапласа может быть найдено методом разделения переменных (методом Фурье) лишь для простейших областей (круг, прямоугольник, шар цилиндр и др.).

Метод преобразования координат. Исходное уравнение с частными производными сводится к обыкновенному дифференциальному уравнению или к другому, более простому уравнению с частными производными с помощью соответствующего преобразования координат (например, поворота координатных осей и т.п.).

Введение новых переменных. Исходное уравнение с частными производными преобразуется к такому уравнению с частными производными для другой неизвестной функции, которое решается легче, чем исходное.

Метод интегральных уравнений. Уравнение с частными производными сводится к интегральному уравнению (уравнение, в котором неизвестная функция стоит под знаком интеграла).

Вариационные методы. Вместо уравнения с частными производными решается некоторая задача минимизации. Оказывается, что функция, доставляющая минимум некоторому выражению, является решением исходного уравнения.

Метод разложения по собственным функциям. Эти собственные функции находятся как решения так называемой задачи на собственные значения, которые соответствуют исходной задаче для уравнения с частными производными.

Метод функций Грина. Начальные и граничные условия заменяются системой простейших источников, и задача решается для каждого простейшего источника. Полное решение исходной задачи получается в результате суммирования решений для элементарных источников.

Классификация методов решения уравнений с частными производными.

Несмотря на то, что с дифференциальными уравнениями в частных производных приходится сталкиваться при решении многочисленных научно-технических задач, получить их решение в явном виде, т.е. в виде конечной формулы, удаётся только в самых простейших случаях. В этой связи приобретают огромное значение приближённые методы решения различных задач для дифференциальных уравнений в частных производных и систем дифференциальных уравнений (ДУ) в частных производных или как говорят задач математической физики.

В данном курсе будут рассмотрены лишь простейшие и наиболее распространённые методы решения задач математической физики. При этом акцент делается на решение задач для линейных ДУ второго порядка с двумя независимыми переменными.

Как и в случае обыкновенных ДУ, приближённые методы решения задач математической физики делятся на две основные группы:

1. приближённо-аналитические методы – методы, в которых приближённое решение получается в аналитической форме, например, в виде отрезка некоторого ряда;

2. численные методы – методы, с помощью которых можно получить таблицу приближённых значений искомого решения в некоторых точках рассматриваемой области.

К группе приближённо—аналитических методов решения краевых задач для ДУ в частных производных относятся, прежде всего, метод Фурье (или метод разделения переменных) и вариационные методы (например, метод Ритца, метод конечных элементов).

Наиболее распространёнными методами численного решения задач для ДУ в частных производных являются:

– Метод сеток, или метод конечных разностей, в котором ДУ или система ДУ предварительно сводится к системе алгебраических уравнений.

– Метод прямых – этот метод в зависимости от способа его реализации может быть отнесён как к первой,так и ко второй группе методов. Название метода прямых связано с тем, что в нём приближённое решение ДУ в частных производных ищется вдоль некоторого семейства прямых, при этом вместо ДУ в частных производных получается система обыкновенных ДУ. Если при этом полученная система обыкновенных ДУ решается в виде системы функций, то речь идёт о приближённо-аналитическом варианте метода прямых; если же полученная система обыкновенных ДУ решается численными методами, тогда метод прямых можно отнести к группе численных методов.

§4. Корректность постановки задач для уравнений математической физики.

Каждое уравнение с частными производными, как и обыкновенное ДУ, имеет бесчисленное множество решений. Поэтому не только получение, но и формальная запись общего решения даже для простейших уравнений в частных производных зачастую вызывает затруднения. Однако ситуация не столь драматична, как это может показаться на первый взгляд, поскольку постановщикам реальных задач, как правило, общее решение и не нужно. Интерес для них представляют те решения, которые обусловлены соответствующими уравнению данными, описывающими изучаемое явление в целом.

При постановке задачи для конкретного уравнения в частных производных, следует позаботиться о том, чтобы добавляемые к уравнению из тех или иных соображений условия выделяли из общего решения некоторое единственное частное решение, и чтобы это частное решение на самом деле существовало в заданном пространстве функций, а также, чтобы оно мало изменялось при малых изменениях добавляемых к уравнению условий (с помощью которых это частное решение выделено из общего).

Обычно корректность постановки задач математической физики связывают со следующими тремя требованиями разрешимости; однозначности; непрерывной зависимости от исходных данных (иначе, устойчивости).

§5. Постановка задач для уравнений математической физики.

Для того чтобы поставить задачу математической физики, необходимо вывести дифференциальное уравнение в частных производных, описывающее рассматриваемый физический процесс, а также сформулировать начальные и краевые условия.

Для уравнений в частных производных, также как и для ОДУ ставятся начальные и краевые задачи.

Начальные условия ставятся для уравнений, содержащих частные производные по времени, при этом сами уравнения, как правило, описывают нестационарные физические процессы. Если одна из независимых переменных играет роль времени, то начальными условиями называются условия, относящиеся к начальному моменту времени (t = t₀), и соответствующая задача, которая заключается в отыскании частного решения, удовлетворяющего данному начальному условию носит название начальной задачи или задачи Коши.

Краевые (граничные) условия ставятся для уравнений, описывающих протекание физических процессов в ограниченных пространственных областях, при этом краевые условия задают (т.е. фиксируют требования) к значениям частного решения на границах пространственных областей.

Задачи математической физики, содержащие начальные и краевые условия, называются начально-краевыми; задачи, содержащие только граничные условия – краевыми, а задачи, содержащие только начальные условия (в бесконечных областях) – начальными задачами или задачами Коши.

Количество начальных и краевых условий и их вид зависят от типов уравнений математической физики, среди которых, как уже указано выше, различают уравнения параболического, гиперболического и эллиптического типа.

Как правило, для уравнений эллиптического типа, описывающих стационарные процессы, задают граничные условия, т.е. ставятся граничные задачи. Для уравнений параболического и гиперболического типа, моделирующих эволюционные процессы и явления, для определённости нужно одновременно задавать условия, начальные по времени и граничные по пространственным переменным, что приводит к постановкам смешанных задач.

Вывод основных уравнений математической физики, начальных и краевых условий к ним даётся в курсе «уравнения математической физики». Здесь будет дана математическая формулировка типовых задач математической физики.

Дата добавления: 2015-09-14 ; просмотров: 2097 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ