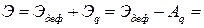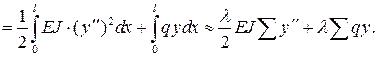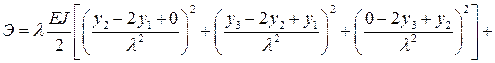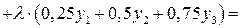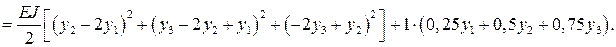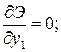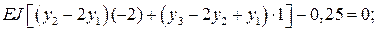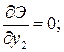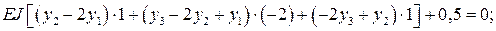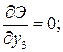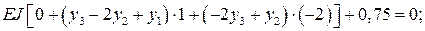Вариационный метод получения уравнения балки

Вариационно-разностный метод в расчетах балок

Здесь используются экстремальные свойства полной потенциальной
энергии системы, а точнее, принцип возможных перемещений по отношению
к энергии системы, который гласит:

! Для системы, находящейся в равновесии, из всех возможных перемещений, удовлетворяющих заданным граничным условиям, в действительности имеют место те, при которых полная потенциальная энергия принимает минимальное значение.

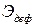
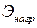
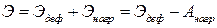
Полная потенциальная энергия системы состоит из энергии ее деформирования и изменения в процессе деформирования потенциала внешней нагрузки :

,

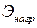
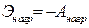
где изменение потенциальной энергии нагрузки равно с обратным знаком работе нагрузки: .

Полная потенциальная энергия систем выражается через перемещения (прогибы) и нагрузки. Функция прогибов входит в выражение энергии в виде непосредственно функции y и ее второй производной. Соответственно выражение полной потенциальной энергии системы можно представить в виде:

. (8.15)

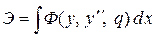
Несложно заметить, что это выражение является функционалом.

Функционал – это функция, которая зависит от одной, либо нескольких функций, и в которой аргумент x в явном виде не присутствует.

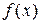
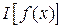
Если для обыкновенной функции значения функции определяются множеством значений аргумента x, то для функционала его значения определяются множеством функций, подчиняющихся определенным (граничным и другим) условиям.

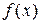
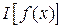
Определение функции , при которой функционал , выраженный с помощью определенного интеграла, получает экстремальное значение, является вариационной задачей.

В рассматриваемых задачах мы ищем функцию прогибов (перемещений), которая соответствует минимальному значению энергии.

Функция, которая удовлетворяет такому условию, называется экстремалью, то есть экстремаль – это решение вариационной задачи.

При использовании конечных разностей мы определяем, как уже указывалось, не саму функцию, а ее значения в ряде точек.

Функционал полной потенциальной энергии представляется в конечно-разностной форме, и берутся производные по параметрам перемещений в точках,
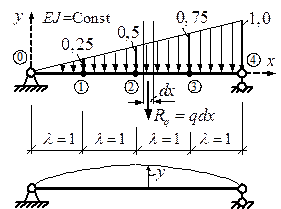
которые на основе принципа возможных перемещений приравниваются к нулю:

(8.16)

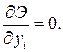
Получаем опять систему алгебраических уравнений, решая которую находим перемещения точек.

Рисунок 8.7 Рассмотрим применение вариационно-разностного метода на примере той же балки (рис. 8.7).

Полная потенциальная энергия балки запишется в виде:

Разбивая балку на четыре участка (рис. 8.7) и учитывая зависимость (8.2) для второй производной, получим:

Применяем теперь к полной потенциальной энергии балки условие ее
экстремальности (8.16) и получаем для каждой из узловых точек уравнения:

; ;

; ;

; .

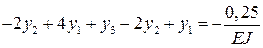
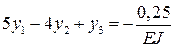
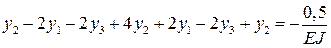
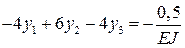
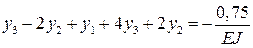
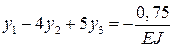
Получаем систему трех уравнений, которая полностью совпадает с системой уравнений, полученной при решении дифференциального уравнения
четвертого порядка (8.13).

Достоинством вариационно-разностного метода является то, что функционал энергии содержит производные только второго порядка.

Расчет балок вариационным методом ритца-тимошенк” (стр. 1 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11

Издательство Российского университета дружбы народов

РасЧет балок вариационным

“Аналитические и Численные методы

Для студентов магистратуры, обучающихся

по специальности “Строительство”

Издательство Российского университета дружбы народов

Российского университета дружбы народов

Расчет балок вариационным методом Ритца-Тимошенко. Методические рекомендации к выполнению курсовой работы по курсу “Численные методы расчета конструкций”. Для студентов магистратуры, обучающихся по специальности «Строительство». — М.: Изд-во РУДН, 2004. — 64 с.

Кратко излагается теоретическое обоснование метода Ритца-Тимошенко. Приводится ряд примеров по расчету балок методом Ритца-Тимошенко. Исследуется сходимость метода сравнением приближенного решения с точным решением сопротивления материалов. Приводятся пример выполнения курсовой работы с использованием микрокалькулятора, и расчет в системе Matcad.

Предназначены для студентов магистратуры при изучении курса “Численные методы расчета конструкций” в качестве пособия при выполнении курсовой работы и освоения методики расчета конструкций вариационным методом Ритца-Тимошенко.

Подготовлена на кафедре сопротивления материалов РУДН.

Ó Издательство Российского университета дружбы народов, 2004 г.

Точные решения известны лишь для ограниченного числа задач теории упругости и строительной механики. При расчете пластин, оболочек, массивных конструкций в большинстве случаев приходится использовать различные приближенные методы. Вариационные методы относятся к наиболее часто используемым в инженерной и научной практике методам приближенного расчета. Вариационные методы основаны на минимизации функционалов, и на основе их можно получать как точные, так и приближенные решения в аналитической или численной форме. Широко применяемый в расчетной практике метод конечного элемента также основан на вариационных принципах строительной механики и теории упругости.

При расчете балок постоянного сечения вариационные методы в основном не используются, так как имеются достаточно простые точные методы решения задач расчета балок методами сопротивления материалов. Однако при расчете стержневых систем на устойчивость и колебания вариационные методы могут применяться. Следует отметить, что широко используемый при расчете стержневых рамных конструкций метод сил основан на вариационных принципах.

Цель данной курсовой работы — научить студента использовать вариационный метод Ритца-Тимошенко на примере расчета балки как наиболее простого объекта исследования. Наличие точного решения сопротивления материалов позволяет исследовать процесс сходимости приближенного решения к точному путем их сравнения. Простота конструкции позволяет получить решение практически с любой степенью точности, проводя расчет с любым числом членов ряда при минимальных затратах труда. Задачи могут также легко программироваться и расчет проведен на ЭВМ с использованием алгоритмических языков программирования Фортран, Паскаль и других современных средств математического обеспечения, например Mathcad.

В работе приводится краткое теоретическое обоснование метода Ритца-Тимошенко, основанного на вариационном принципе Лагранжа. Приводится ряд расчетов шарнирно опертой балки с исследованием сходимости решения к точному решению, полученному методами сопротивления материалов. Далее приводится пример выполнения курсовой работы с использованием микрокалькулятора и на основе приведенной в приложении программы на алгоритмическом языке Паскаль, а также средств системы Mathcad.

При выполнении курсовой работы студент имеет право проводить расчет с применением любого из указанных или других альтернативных средств.

РасЧет балок Вариационным методом

Метод Ритца-Тимошенко, как и большинство вариационных методов решения задач теории упругости, основан на принципе Лагранжа — принципе минимума полной энергии деформаций [1, 2].

Принцип Лагранжа. Из всех кинематически возможных напряженно-деформированных состояний твердого деформируемого тела для действительного напряженно-деформированного состояния достигается минимум полной энергии деформаций.

Кинематически возможным деформированным состоянием называется любое деформированное состояние тела, отвечающее заданным условиям перемещения отдельных точек рассматриваемой конструкции. В основном это условия закрепления точек конструкции — граничные кинематические условия. В стержневых рамных конструкциях к кинематическим условиям можно отнести и условия сопряжения стержней. Например, сохранение угла между жестко соединяемыми в узле стержнями.

Согласно принципу Лагранжа для любого приближенного решения, описывающего напряженно-деформированное состояние конструкции, значение полной энергии деформаций будет больше полной энергии деформаций, полученной для действительного (точное решение) напряженно-деформированного состояния.

Полная энергия деформаций определяется по формуле:

где Э — полная энергия деформаций; U — потенциальная энергия деформаций (работа внутренних сил); T — работа внешних сил;

;

, (1.1а)
s, t — нормальные и касательные напряжения; e, g — линейные и угловые относительные деформации; X, Y, Z — проекции объемных сил, qx, qy, qz проекции поверхностной распределенной нагрузки на оси прямоугольной системы координат; u, v, w — проекции перемещения точки в прямоугольной системе координат.

Полная энергия деформаций (1.1, 1.1а) является функционалом. В курсе вариационного исчисления [3,4], изучающего свойства функционалов, показано, что необходимым условием экстремума функционала является равенство нулю вариации функционала. Вариация (приращение) функционала является аналогом дифференциала (приращения) функции в математическом анализе.

Таким образом, условие достижения экстремума (минимума) полной энергии деформаций имеет вид:

где d — знак вариации функционала.

1.1. Алгоритм расЧета поперечного изгиба балок

Согласно теории сопротивления материалов при поперечном изгибе балок в поперечном сечении балки возникают нормальные напряжения sх и касательные напряжения tху, остальные напряжения равны нулю. Следовательно, потенциальная энергия деформаций определяется выражением:

. (1.1.1)

При этом потенциальная энергия, определяемая касательными напряжениями, обычно составляет 1-2%, и влиянием этого слагаемого в функционале энергии пренебрегают. Окончательно получаем формулу потенциальной энергии деформаций балки:

, (1.1.2)

где Мz — изгибающий момент в поперечном сечении балки, Jz — момент инерции поперечного сечения, Е — модуль упругости материала балки, у — координата точки поперечного сечения балки, l — пролет балки.

При выводе формулы (1.1.2) использовались формула закона Гука и формула нормальных напряжений при поперечном изгибе балки.

Используя формулу дифференциального уравнения прогибов оси балки , получим формулу потенциальной энергии деформаций балки в перемещениях:

, (1.1.3)

здесь у — прогиб оси балки.

Работа внешних сил — поперечной нагрузки балки (рис. 1.1.1) определяется по формуле:

. (1.1.4)

В формуле (1.1.4) интеграл представляет работу распределенной нагрузки. При этом q(х) изменяется по любому закону, в том числе функция нагрузки может быть кусочно-переменной функцией. В этом случае интеграл берется по соответствующим участкам пролета балки. В частности если на участке балки распределенная нагрузка отсутствует q(х)=0, то интеграл на этом участке равен нулю. Суммы в выражении работы сосредоточенных поперечных сил и моментов показывают, что нужно учесть влияние всех действующих сосредоточенных сил и моментов.

На рис.1.1.1 показаны положительные направления внешних сил.

Прежде чем изложить алгоритм метода Ритца-Тимошенко, проведем замену переменной х, перейдя к безразмерным координатам, положив:

. (1.1.5)

При этом диапазон аргумента х — 0 £ х £ а , заменяется на диапазон изменения безразмерного аргумента x — 0 £ x £ 1. Использование безразмерных координат имеет много преимуществ и позволяет снизить трудоемкость вычислительного процесса и уменьшить возможность ошибок из-за неправильного использования размерных величин.

Вариационные подходы к нахождению собственных частот балок переменного сечения Текст научной статьи по специальности « Физика»

Аннотация научной статьи по физике, автор научной работы — Гусев Б.В., Саурин В.В.

Работа состоит из введения и восьми разделов. Во введении обсуждается актуальность вопросов, связанных с изучением колебаний неоднородных балок. Проводится анализ публикаций и полученных результатов в данной области. Вторая часть посвящена формулировке краевой задачи нахождения собственных частот неоднородной балки в рамках гипотез Эйлера-Бернулли. Следующий параграф касается вопросов, связанных с различными классическими вариационными формулировками спектральных задач, возникающих в теории. Обсуждаются особенности применении принципа Гамильтона и дополнительного к нему для такого типа краевых задач. В четвертом разделе описывается метод интегродифференциальных соотношений, который является альтернативным к классическим вариационным подходам. Далее исследуются возможности построения различных двусторонних энергетических оценок качества и приближенных решений, вытекающих из метода интегродифференциальных соотношений. В шестом параграфе обобщаются результаты, полученные и обсужденные в предыдущих разделах, и вводится однопараметрическое семейство квадратичных неотрицательных функционалов, условия стационарности которых совместно с интегродифференциальными ограничениями составляют полную систему уравнений, описывающую динамическое поведение неоднородных балок. В седьмом разделе рассматривается связь вариационных задач, получаемых с использованием введенного семейства функционалов с классическими вариационными принципами. В завершающей части на основе численного модельного примера обсуждаются преимущества вариационной техники в задачах о свободных колебаниях неоднородных балок, как геометрически, так и функционально.

Похожие темы научных работ по физике , автор научной работы — Гусев Б.В., Саурин В.В.

Текст научной работы на тему «Вариационные подходы к нахождению собственных частот балок переменного сечения»

Вариационные подходы к нахождению собственных частот балок переменного сечения

Гусев Борис Владимирович,

д.т.н., проф., член-корреспондент РАН,

заведующий кафедрой Российский университет транспорта

Саурин Василий Васильевич,

доктор физико-математических наук, ведущий научный сотрудник, Институт проблем механики им. А.Ю. Ишлинского РАН

Работа состоит из введения и восьми разделов. Во введении обсуждается актуальность вопросов, связанных с изучением колебаний неоднородных балок. Проводится анализ публикаций и полученных результатов в данной области. Вторая часть посвящена формулировке краевой задачи нахождения собственных частот неоднородной балки в рамках гипотез Эйлера-Бернулли. Следующий параграф касается вопросов, связанных с различными классическими вариационными формулировками спектральных задач, возникающих в теории. Обсуждаются особенности применении принципа Гамильтона и дополнительного к нему для такого типа краевых задач. В четвертом разделе описывается метод интегродифференциальных соотношений, который является альтернативным к классическим вариационным подходам. Далее исследуются возможности построения различных двусторонних энергетических оценок качества и приближенных решений, вытекающих из метода интегро-дифференциальных соотношений. В шестом параграфе обобщаются результаты, полученные и обсужденные в предыдущих разделах, и вводится однопараметрическое семейство квадратичных неотрицательных функционалов, условия стационарности которых совместно с интегродиф-ференциальными ограничениями составляют полную систему уравнений, описывающую динамическое поведение неоднородных балок. В седьмом разделе рассматривается связь вариационных задач, получаемых с использованием введенного семейства функционалов с классическими вариационными принципами. В завершающей части на основе численного модельного примера обсуждаются преимущества вариационной техники в задачах о свободных колебаниях неоднородных балок, как геометрически, так и функционально.

Ключевые слова: динамика, балка переменного сечения, собственные колебания, численные методы, структурная неоднородность, метод конечного элемента, функционально градуированные материалы.

Многие балки, применяемые в технике и строительстве, характеризуются переменными геометрическими и физическими параметрами. Типичным случаем является коническая балка. Кроме того, например, балка при неравномерном распределении температуры имеет переменные физические свойства. Наличие переменных параметров значительно затрудняет динамический анализ таких балок.

Изучение динамики конструкций в настоящее время становится все более важным для инженеров-строителей, поскольку многоэтажные сооружения становятся относительно более гибкими. Такая тенденция в строительстве, как правило, приводит к увеличению амплитуд колебаний зданий. Поэтому в некоторых случаях необходимо рассчитать динамические характеристики высотных конструкций уже на этапе проектирования. При анализе свободных колебаний консольных высотных зданий их можно моделировать, в первом приближении, балками с переменным поперечным сечением.

В течение последних нескольких десятилетий значительное количество публикаций, представляющих либо аналитические, либо численные решения, были посвящены поперечным колебаниям неоднородных балок и равномерно вращающихся балок. Характеристическая черта управляющих дифференциальных уравнений поперечных колебаний неоднородных балок состоит в том, что они представляют собой линейные уравнения четвертого порядка с переменными коэффициентами.

Поперечные колебания неоднородных балок изучались многочисленными исследователями вследствие их значимости для гражданского строительства. Эти исследования представляют из себя либо аналитические [1]-[4], либо приближенные решения [5].

Аналитические решения получены в виде ортогональных полиномов, функций Бесселя [2], гипергеометрических рядов [3], степенных рядов, полученных методом Фробениуса [4]. Метод, в котором уравнения движения неоднородных балок преобразуют в одно, описывающее

движение некоторой однородной балки, приведен в работе Abrate [17]. Приближенные методы, такие как метод Рэлея-Ритца, с использованием либо ортогональных многочленов [5], либо рядов Фурье в качестве пробных функций, метод Ритца, метод Галеркина, метод конечных разностей или метод конечного элемента были использованы для нахождения приближенных собственных частот неоднородных балок.

Среди результатов, представленных в литературе, точные решения в замкнутой форме представляют особый интерес из-за того, что они служат критериями, по которым можно оценить точность различных приближенных решений, полученных с помощью методов Релея-Ритца, Бубнова-Галеркина, конечных разностей, конечных элементов, дифференциальных квадратур и др. [6]. Кроме того, они служат тестовой базой для разработки новых систем численного решения краевых задач. Пакет, состоящий из точных решений нескольких краевых задач Штурма-Лиувилля второго порядка, который представляет собой реалистичный тест производительности доступных в настоящее время автоматических кодов для нахождения собственных значений классических задач Штурма-Лиувилля, представлен в работе Pryce [16].

Abrate [17] представил точные решения для нового класса конических балок. Он показал, что для некоторых неоднородных стержней уравнение движения можно преобразовать к уравнению однородной балки. Для проверки этих результатов была разработана общая процедура анализа свободных колебаний конических балок. Подход Рэлея-Ритца использован для формулировки задачи, и смещения раскладываются в ряд полиномиальных функций, которые могут удовлетворять граничным условиям на одном конце. Если концы стержня полностью фиксированы, то собственные значения неравномерного континуума такие же, как и у однородных балок. Для других граничных условий на концах также получены точные решения. Эффективная процедура разработана и применена для анализа колебаний неоднородной балки общей формы поперечного сечения и произвольными граничными условиями. Для нахождения фундаментальной собственной частоты неоднородной балки получены простые формулы.

Firouz-Abadi и др. [18] исследовали сужающеюся балку приближенным аналитическим методом и представили решение на основе приближений Венцеля, Крамерса, Бриллуина для свободных поперечных колебаний балок с переменным поперечным сечением.

Hsu и др. [7] применили модифицированный метод разложения Адомиана (AMDM) для неоднородной балки Эйлера-Бернулли. Полученные

решения хорошо согласуются с аналитическими и численными результатами, приведёнными в литературе.

В прошлом было проведено много исследований свободных колебаний неоднородных балок. Однако решения в замкнутой форме до сих пор получены для малого числа задач. Показано, что аналитические решения можно найти для некоторых особых случаев, например, как структуры с экспоненциально изменяющимся поперечным сечением. Обычно для построения решения применяют различные численные методы, такие как метод конечных элементов, метод конечных разностей и т. д.

Для уравнений в частных производных, решения о свободных колебаниях получаются в виде тригонометрических и гиперболических функций, гипергеометрических функций, функций Бесселя. Эти решения описывают поведение балки для различных граничных условий.

Wang [19] получил решения в замкнутой форме для свободных изгибных колебаний стержня с переменной распределённой жёсткостью, но однородно распределённой массой.

Li и др. [20] смоделировали рамную конструкцию в виде поперечной балки с переменным поперечным сечением. Последняя часть этой работы посвящена конструкции каркасно-сдвиговых стенок, которые моделировались как призматическая балка Тимошенко. Однако в целом невозможно или, по крайней мере, очень сложно получить точное аналитическое решение дифференциальных уравнений для свободных колебаний стержней с переменной массой и жесткостью, но иногда точное решение может быть получено выбором подходящего распределения массы и жесткости вдоль стержня.

Большинство рассмотренных задач относятся к исследованию поперечных колебаний сужающихся балок. Эти результаты можно систематизировать следующим образом: балки с круглым поперечным сечением либо усеченные [1], имеющими один острый конец, либо два острых конца [9]; балки с прямоугольным поперечным сечением и с постоянной шириной, с постоянной толщиной [4] или пирамидой [1].

Heidebrecht [21] с использованием тригонометрического ряда Фурье нашел из частотного уравнения приближенные собственные частоты и формы колебаний неоднородной просто опертой балки. Branch [22] оптимизировал основную частоту поперечных колебаний стержней с переменным поперечным сечением, для которых допустимо изменение формы сечения по длине так, что его момент инерции линейно связан с площадью. Gupta [23] численно нашел собственные частоты и формы колебаний сужающихся балок с использованием метода конечных элементов.

Изгибные колебания конических балок были исследованы во многих работах. Naguleswaran [24] определил приближенные собственные частоты одноконусных балок и двойных конических стержней прямым решением уравнения формы колебаний на основе метода Фробениуса. Он также исследовал однородную балку прямоугольного сечения, одна сторона которой изменяется в виде квадратного корня осевой координаты.

Zhou [25] исследовал колебательные характеристики конических балок с непрерывно изменяющимся прямоугольным поперечным сечением. Теории изгиба Бернулли-Эйлера и Тимошенко были использованы для описания движения балки. В качестве допустимых функций были разработаны новые балочные функции, которые являются полным решением задачи об изгибе конической балки при произвольной статической нагрузке. Вековое уравнение выводится с помощью метода Рэлея-Ритца. Показано, что собственные частоты могут быть получены с высокой точностью при использовании лишь небольшое числа членов статических функций.

В нескольких работах были рассмотрены балки прямоугольного сечения, в которых ширина изменялась с любой положительной полиномиальной степенью продольной координаты, а толщина была либо постоянной, либо линейной, либо также менялась с любой положительной полиномиальной степенью. Обсуждалась возможность изменения толщины балки в соответствии с параболическим законом при постоянной ширине или нулевой ширине на обоих концах балки. Cranch [26] представил решения в замкнутой форме (в терминах функций Бесселя и / или степенных рядов) для собственных частот и форм колебаний неограниченных неоднородных балок с постоянной толщиной и экспоненциально меняющейся шириной для четырех видов поперечных сечений.

Ece и др. [27] исследовали колебания изотропной балки с переменным поперечным сечением. В этом случае управляющее уравнение сводится к одному обыкновенному дифференциальному уравнению относительно пространственной координаты для семейства поперечных сечений с экспоненциально изменяющейся шириной. Получены аналитические решения задач о собственных колебаниях балки для трёх различных типов граничных условий: простое опирание, жесткое защемление и свободные концы. Собственные частоты и формы колебаний были определены для каждого набора граничных условий. Результаты показали, что такое изменение поперечного сечения существенно влияет на собственные частоты и формы колебаний. Амплитуда колебаний увеличивается для расширяющихся балок, в то время как она уменьшается для сужающихся.

Интерес исследователей к задачам о колебаниях неоднородных одномерных структур в первую очередь связан с исследованием Eisenberger [28] конических стержней, показывающее, что собственные частоты слабо зависят от конуса. Кроме того, Graf [29] упомянул, что для стержней с коническим поперечным сечением уравнение движения можно получить в виде волнового уравнения путем соответствующего изменения переменной. Изучение конических стержней важно для изучения основ и динамики композитных структур, подверженных высокоскоростному удару. В этих случаях динамический отклик полуплоскости на поверхностную нагрузку можно точно определить с использованием конической модели.

Предыдущие исследования колебаний конических балок включают исследование Conway и др. [30], который получил точное решение уравнения движения для конической балки как разложение по функциям Бесселя и представил детерминантные уравнения для нахождения собственных частот таких балок для четырех наборов граничных условий. Mabie [31] использовал тот же подход для изучения защемленных балок с постоянной шириной и линейно изменяющейся толщиной или постоянной толщиной и линейно изменяющейся шириной. Он также рассматривал полиномиальное изменение площади поперечного сечения балки и момента инерции для получения собственных частот двойной конической балки.

Bayley [32] впервые использовал подход Рэ-лея-Ритца и численно решил частотное уравнение, чтобы найти собственные частоты сужающихся консольных балок. Существенные граничные условия на другом конце выполняются с использованием метода множителей Лагранжа. Площадь поперечного сечения и момент инерции балки считаются произвольными полиномиальными функциями осевой координаты. Результаты представлены для нескольких частных случаев и показывают отличное согласие с ранее опубликованными результатами. Предложенный метод прост в применении и эффективен. Кроме того, простые формулы для предсказания основных частот получены с использованием одномерных приближений Рэлея-Ритца. Показано, что эти формулы являются точными и должны представлять интерес для конструкторов.

2. Постановка задачи

Рассмотрим тонкую балку длины L , которая может быть описана уравнениями в рамках гипотез Эйлера-Бернулли. Плоские поперечные движения балки в рамках рассматриваемой модели описываются линейным уравнением в частных производных

р(х)уи + (£Л(х)у„ )„ = д(х, О х е (0, Ь). (1)

Здесь у — поперечные перемещения точек центральной линии балки, р — линейная плотность материала балки, Е — модуль Юнга, д(х,г) — внешняя распределенная нагрузка, Л (х) — момент инерции поперечного сечения. Без потери общности будем считать, что внешняя распределенная нагрузка отсутствует, т. е.

Введем новые переменные р(г, х) и ш(г, х), которые характеризуют поведение системы и, в то же самое время, имеют ясный физический смысл. Функция р(г, х) является линейной плотностью импульса, а ш(г, х) — изгибающим моментом в поперечном сечении балки.

Уравнения в линейной теории (в дальнейшем уравнения состояния), связывающие плотность импульса р(г, х) со скоростями точек системы

у1 (х, t), а также момент ш(г, х) с кривизной балки ухх(х,г) , вызванной изгибом, могут быть соответственно записаны в виде

Введем вспомогательные функции г и 4

Тогда уравнения состояния (2) могут быть представлены в виде

Используя соотношения (2), уравнение движения упругой балки (1), записанное в перемещениях, можно выразить через функции момента ш(г, х) и импульса р(г, х):

Поскольку выражение (5) связывает распределенные инерционные, упругие и внешние силы, то это соотношение будем называть уравнением динамического равновесия.

Для того чтобы сформулировать задачу нахождения собственных частот колебаний балки представим все введенные функции, которые зависят от времени, в виде

у( х, г) = у( х)в’с г( х, г) = ](х)в»1

р( х, г) = р( х)г’с 4( х, г) = 4( х)в’ю

Подставляя функции из (6) соответственно в выражения (2), (3) и (5) получим

В дальнейшем знак тильды опускается.

В данной работе ограничимся рассмотрением случая простого опирания, когда отсутствуют перемещения и внешние моменты в торцевых сечениях стержня. Другими словами, линейные граничные условия выражаются через краевые значения функций момента ш и перемещения у в виде

3. Классические вариационные формулировки

При решении краевой задачи (7), (8) и (10) необходимо учитывать, что функция изгибной жесткости ЕЛ может иметь разрывы в некоторых точках балки. В этих точках могут существовать особенности решения, для учета которых обычно используют вариационные подходы [35]. В динамике классические вариационные принципы сформулированы для периодических и краевых по времени задач и ограниченного класса условий, заданных на концах балки. Приведем два примера вариационных формулировок, которые потребуются в дальнейшем для анализа исходной задачи.

Рассмотрим движения упругой балки на фиксированном интервале г е [0, Т]. Если в начале (t = 0) и в конце ( = т) движения заданы перемещения у(0, х) = у°(х) и у(Т’х) = ут (х) , то существуют функции кинетической энергии

К и полной потенциальной энергии и, выраженные через перемещения, и при вариациях

не изменяются изгибающие моменты ш и

перерезывающие силы х на краях балки, из принципа виртуальной работы следует принцип стационарности Гамильтона

В соответствии с этим принципом граничные условия в перемещениях являются главными, т.е. должны строго выполняться. Если на концах балки условия заданы через изгибающий момент или перерезывающую силу, то они являются естественными граничными условиями и учитываются в обобщенном смысле через соответствующие линейные члены функционала Н .

В этой вариационной задаче подразумевается строгое выполнение локальных соотношений (7). Уравнение движения (9) и краевые условия (10) являются необходимыми условиями стационарности гамильтониана Н.

Если заданы начальные и терминальные распределения импульса р(0, х) = р0(х) и

р(Т, х) = рт (х) , то существуют функции дополнительной кинетической энергии Кс и полной дополнительной энергии ис, выраженные соответственно через импульс р и момент т, и при вариациях равновесных полей 5р , 6т граничные перемещения у и наклон центральной линии ух не меняют свои значения, можно

сформулировать принцип стационарности дополнительной энергии

5Нс = 0, Нс =| (Кс — ис С,

В этой формулировке граничные условия, выраженные через изгибающие моменты являются главными, т.е. должны строго выполняться. Кроме того, функции момента т и импульса р обязаны удовлетворять уравнению динамического равновесия (5).

Отсюда следует, что граничные условия, заданные в силах, не входят в функционал Нс ,

определенный в (12). Если же граничные условия заданы в перемещениях, то именно эти соотношения являются естественными граничными условиями для дополнительного принципа Гамильтона и учитываются через соответствующие линейные члены функционала Нс .

Уравнения состояния (2) и граничные условия, заданные в перемещениях, эквивалентны условиям стационарности дополнительного к гамильтониану функционала Нс .

Оба принципа (11) и (12) сформулированы для краевых динамических задач линейной теории упругости и, вообще говоря, в представлен-

ном виде не могут быть применены для решения начально-краевой задачи.

4. Метод интегро-дифференциальных соотношений

В предлагаемом подходе вместо уравнений состояния балки (2) вводится в рассмотрение одно интегральное соотношение, связывающее функции импульса р и момента т с функцией перемещений у .

В книге [36] дана следующая интегро-дифференциальная формулировка задачи о

движении упругой балки (7)—(10): найти такие

неизвестные поля плотности импульса р , мо* *

мента т и перемещений у , которые удовлетворяют следующему интегральному соотношению

Ф = |р(р, т, у) Са = 0, р = -р) + £/#2), (13) а 2

при строгом выполнении условий (9), (10). Здесь введена область пространственно-временная область а = (0,1) х (0,Т) с границей

да в пространстве координаты х и времени I. Интеграл (13) вычисляется по прямоугольной области а (д& = сСхсИ).

Подынтегральная функция, определенная в (13) через функции г и ^ из (8), является неотрицательной по построению. Из этого свойства следует, что интеграл Ф также неотрицателен для произвольных функций р , т и у . Это обстоятельство позволяет свести интегродиф-ференциальную задачу (7), (9), (10), (13) к следующей минимизационной. Найти такие допус-* * *

тимые функции р , т и у , которые доставляют минимальное (нулевое) значение функционалу Ф :

Ф = шт Ф( р, т, у) = 0

при строгом выполнении ограничений (7), (9) и (10).

Функционал Ф можно переписать в следующем виде

Ф = ^1 -2Т2 +Т3, т, у) сЮ, I =1,2,3,

V =1 (-Р®У + Ыу1.) =1 (( + ту*; ) ^3 =1 ^рр+

Подынтегральные выражения V , * = 1,2,3

представляют собой различные представления линейной плотности полной механической энер-

гии упругой балки. Функция у/1 зависит только от поперечных перемещений y , в то время как в выражение для щъ, квадратичное по p и m , перемещения не входят. Смешанная билинейная функция плотности энергии щ2 не зависит

явно от инерционных и упругих свойств балки.

Так как решение вариационной задачи (14) может быть разрывным, уравнение динамического равновесия (9) определено только тогда, когда функция моментов m дважды непрерывно дифференцируема по x .

В вариационной формулировке условие динамического равновесия необходимо понимать в следующем интегральном смысле: для любой

области Q cQ с кусочно-гладкой границей

дй и любой непрерывно дифференцируемой

по x функции перемещений y( x, t) = y( x)* em

(по аналогии с (6)) выполняется соотношение

J (iapy — myxx) dQ = J RmVx » (n,P — nxmx)у]ddQ

Здесь nx и nt проекции единичной внешней

нормали к границе дй соответственно на оси x и t. Можно показать, что для сформулированной минимизационной задачи необходимо, чтобы на линиях х = const в области Q допустимые перемещения y и моменты m задавались непрерывно дифференцируемыми по x функциями. На линиях t= const поля плотности импульса p и перемещений y непрерывны, на наклонных кривых (| nx || nt 0) вдоль нормали должно быть непрерывным соотношение nxmx — ntp .

5. Энергетические оценки качества решения

Используя функционал Ф и энергетические интегралы , i = 1,2,3 (введенные в (15), для произвольных допустимых полей импульсов p , моментов m и перемещений y , удовлетворяющих ограничениям (10) и (16), можно предложить ряд критериев, которые могут характеризовать совершенство приближенного решения. Интегральное качество приближенных функций p , m , y можно оценивать, например, в соответствии с величиной безразмерного соотношения

Точность распределения энергии для некоторого допустимого движения р(х, г), ш(х,г), у(х, г) в области О характеризует подынтегральная функция р(р, ш, у), определенная в (13). Еще одним показателем качества приближенных движений является разность между запасенной балкой в процессе движения полной механической энергией и работой внешних сил. Для оценки этой величины введем еще одну функцию линейной плотности механической энергии ц и соответствующую ей энергию и

ц = -1 — + Л 1= К (р) + А(у), Ч = \иць,

где А(у) заданная в перемещениях линейная плотность упругой энергии из (11), Кс (р) —

выраженная через импульсы линейная плотность кинетической энергии из задачи (12). Аналогично выражениям из (15) определен интеграл по времени ¥ от полной механической энергии балки иц.

Из непрерывности по времени допустимых импульсов р и перемещений у следует непрерывность функции энергии иц по времени.

Дифференцируя эту функцию по времени и дважды производя интегрирование по частям, получаем выражение для мощности с учетом условия динамического равновесия (16)

Ж = ‘ю[шух -шху£=0, и0 = ‘Ю^-гр + ЕЛух)).

Здесь Ж — работа внешних сил, и0 — «паразитная» энергия, которая является малой величиной, когда приближенное движения близко к действительному, т.е. при малых значениях отношений А’ (‘ = 1. 4) заданных в (17).

6. Семейство вариационных формулировок

Используя свойства квадратичных функционалов, обсуждавшийся ранее, введем семейство эквивалентных вариационных формулировок для задач о движениях упругой балки

■ = \ра(р, ш, у) ё О = 0, ра= — (рг2 +аЕЛ%2), аФ 0, ^ 2

для которых, как будет показано далее, стационарные условия при выполнении ограниче-

ний (10) и (16) эквивалентны определяющим соотношениям состояния упругой балки (7). В выражении для функционала Фа из (20) а — ненулевая действительная константа. При а = 1 интеграл Фа совпадает с неотрицательным функционалом Ф, введенным в (13). Если а > 0 , то каждому функционалу Фа соответствует своя задача условной минимизации эквивалентная задаче (10), (14) и (16).

Обозначим действительные и произвольно

выбранные допустимые импульсы, моменты,

перемещения, через р , т , у и р , т, у соответственно и положим, что выполняются равенства р = р* +5р, т = т* + 5т ,

у = у * +5у . Тогда предполагая, что на точном

решении р , т , у значение функционала Фа равно нулю: Фа(р*,т*,у*) = 0, на допустимых полях р , т , у получаем

(р,т,у)=2Г^р!’/й 5т, 5у) = Ф+5Фа 8Фа=2 ОрКр, у) ^у-^рр)+аЕ7^(т, у) <зу^ -^^О,

где 5 Фа первая, а 52Фа вторая вариации функционала Фа . Отсутствие членов более высокой степени объясняется квадратичной формой функционала относительно неизвестных функций.

Для произвольных значений а можно дать общую вариационную формулировку краевой

задачи движения упругой балки: найти неиз-

вестные функции р , т , у , доставляющие при выполнении ограничений (10) и (16) стационарные значения функционалу Фа

5Ъа=5р Фа+5„ Фа+5у Фа= 0 (22)

где 5рФа , 5тФа , 5уФа — первые вариации

относительно неизвестных р, т, у соответственно.

После интегрирования по частям с учетом ограничений (10) и (16) получаем выражения для первых вариаций

5рФа+5тФа = -\(г5р + а5т )сС О,

+ а[5ух — (Е]4)х 5у] с + Г [ рг5у\ сСх.

Из выражений (23) видно, что первые вариации функционала Фа равны пулю на любых

допустимых вариациях функций 5р , 5т, 5у , если выполняются соотношения (7).

Получим в явном виде необходимые условия стационарности функционала Фа (уравнения

Эйлера). Для этого надо учесть связь между функциями импульса р и момента т , которая определяется уравнением динамического равновесия (9), а значит и связь между их вариациями 5р и 5т:

Вводя вспомогательную функцию

находим с учетом ограничения (24) выражения для первых вариаций 5Фа

5тФа = -\(хх + а) Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

Здесь управляющий параметр h1 , который может изменяться в следующих пределах 0 0, Ф0 =^EJylx — m^dx, i = 1. Nd

Стоит отметить, что применение вариационной техники в такой задаче приводит к появлению комплексных собственных значений. Можно показать (см., например, [35]), что действительные собственные частоты приближенного спек-

тра соответствуют точным значениям частот. На Рис. 2 показано поведение четвертого комплексного собственного значения в зависимости от степени аппроксимации N0. Увеличение этого параметра приводит к значительному уменьшению мнимых частей. Видно, что линия, соответствующая приближенным собственным частотам, вертикально втыкается в вещественную ось. Поэтому угол наклона частотной линии и расстояние до действительной оси могут служить специальным видом оценки качества полученных частот. В расчетах параметр N0 менялся от N0 = 7 до N0 = 25 .

Рис. 2. Действительные и мнимые части четвертой собственной частоты балки для различных полиномиальных приближений.

На Рис. 3 изображены первые собственные формы свободных колебаний незакрепленной балки с переменным поперечным сечением. Функция , введенная в уравнении (15) представлена на Рис. 4 для первой моды колебаний при N0 = 25 . Можно отметить заметное биение

функции, а также значительный ее рост в окрестностях концов балки.

Рис. 3. Первые пять собственных форм колебаний опертой балки переменного сечения.

На Рис.5 показана характерная сходимость пяти первых собственных частот (кривые отмечены соответствующими номерами) относительно числа степеней свободы (ЫйОР). Значения параметра А1 приведены в логарифмиче-

ском масштабе. Можно отметить довольно быструю сходимость (экспоненциальную). Все линии линейно убывают с ростом числа степеней свободы.

Рис. 4. Распределение локальной ошибки по длине балки для первой формы собственных колебаний.

Рис. 5. Сходимость пяти первых собственных частот относительно числа степеней свободы.

Рис. 6. Зависимость значения первой собственной часто-

ты в зависимости от значения параметра 1 .

На Рис. 6 показана зависимость первой собственной частоты для балок переменного сече-

ния, характеризующихся параметром К1. Важно

отметить что существует ярко выраженный максимум у представленной кривой

ю= 190.105 Гц при К = 0 233 . При этом отличие максимальной частоты от значения первой частоты балки постоянного сечения (Ю = 171.496 Гц при 10.85% .

h1 = 0.6) составляет

Разработан регулярный вариационный подход нахождения собственных частот и форм колебаний неоднородных балок путем сведения краевой задачи по времени к системе обыкновенных дифференциальных уравнений с переменными коэффициентами. Изучены и обсуждены свойства квадратичных соотношений и их значение для решения различных спектральных задач. В качестве примера представлены интег-родифференциальные формулировки задачи о свободных колебаниях балки с квадратично меняющейся по ее длине строительной высотой. Построены оптимальные формы бетонных балок с максимальной первой собственной частотой. Показано, что предложенные двусторонние критерии качества приближенного решения позволяют получать высокоточные решения для математических моделей малой размерности.

В будущих работах авторы планируют уделить внимания разработке эффективных численных стратегий и процедур построения достоверных решений методом конечных элементов с использованием разработанной вариационной техники на основе метода интегро-дифференциальных соотношений.

1. Rosa M.A. De, Auciello N.M. Free vibrations of tapered beams with flexible ends // Computers & Structures. 1996. V. 60, № 2. pp. 197-202.

2. Cranch E.T., Adler A. Bending vibrations of variable section beams // American Society of Mechanical Engineers. 1956. V. 23, № 1. pp. 103108.

3. Caruntu D.I. On nonlinear vibration of nonuniform beam with rectangular cross-section and parabolic thickness variation // Solid Mechanics and its Applications. 2000. V. 73. pp. 109-118.

4. Chaudhari T.D., Maiti S.K. Modelling of transverse vibration of beam of linearly variable depth with edge crack // Engineering Fracture Mechanics. 1999. V. 63. pp. 425-445.

5. Auciello N.M. On the transverse vibrations of non-uniform beams with axial loads and elastically restrained ends // International Journal of Mechanical Sciences. 2001. V. 43. pp. 193-208.

6. Elishakoff I. Eigenvalues of Inhomogeneous Structures: Unusual Closed-form Solutions. Boca Raton, FL: CRC Press, 2005.

7. Hsu J.C., Lai H.Y., Chen C.K. Free vibration of non-uniform Euler-Bernoulli beams with general elastically end constraints using Adomian modified decomposition method // Journal of Sound and Vibration. 2008. V. 318. pp. 965-981.

8. Franciosi C., Mecca M. Some finite elements for the static analysis of beams with varying cross section // Computers and Structures. 1998. V. 69, № 2. pp. 191-196.

9. Jang S.K., Bert C.W. Free vibration of stepped beams: Exact and numerical solutions // Journal of Sound and Vibration. 1989. V. 130. pp. 342-346.

10. Prediction of the influence of temperature field on the critical speeds of a rod-fastened rotor / S. Liu, Y. Zhang, Z. Du [and others.] // Gas Turbine Technology. 2011. V. 2. pp. 20-23.

11. Simsek M., Cansiz S. Dynamics of elastically connected double-functionally graded beam systems with different boundary conditions under action of a moving harmonic load // Composite Structures. 2012. V. 94, № 9. pp. 28612878.

12. Gorman D.J. Free vibration analysis of beams and shafts. New York: Wiley, 1975.

13. Rao S. Ramalingerswara, Ganesan N. Dynamic response of tapered composite beams using higher order shear deformation theory // Journal of Sound and Vibration. 1995. V. 187, № 5. pp. 737-756.

14. Calim F.F. Free and forced vibrations of non-uniform composite beams // Computers & Structures. 2009. V. 88, № 3. pp. 413-423.

15. Pakar M.B. Accurate analytical solution for nonlinear free vibration of beams // Structural Engineering and Mechanics. 2012. V. 43, № 3. pp. 337-347.

16. Pryce J.D. A test package for Sturm-Liouville solvers // ACM Transactions on Mathematical Software. 1999. V. 25, № 1. pp. 21-57.

17. Abrate S. Vibration of non-uniform rods and beams // Journal of Sound and Vibration. 1995. V 185, № 4. pp. 703-716.

18. Firouz-Abadi R.D., Haddadpour H., Novinzadeh A.B. An asymptotic solution to transverse free vibrations of variable-section beams // Journal of Sound and Vibration. 2007. V. 304. pp. 530-540.

19. Wang G.Y. Vibration of Building and Structures // Beijing Technology Science Press. 1978. pp. 168-178.

20. Kang Y. A., Li X. F. Bending of functionally graded cantilever beam with power-law nonlinearity subjected to an end force // International Journal of Non-Linear Mechanics. 2009. V. 44, № 6. pp. 696703.

21. Heidebrecht D.H. Vibration of non-uniform simply supported beams. Journal of the Engineering Mechanics Division. 1967. pp. 1-15.

22. Branch R.M. On the extremal fundamental frequencies of vibrating beams // Journal of Sound and Vibration. 1968. №. 4. pp. 667-674.

23. Gupta A. Vibration of tapered beams // Journal of Structural Engineering. 1985. V. 111, № 1. pp. 19-36.

24. Naguleswaran S. Vibration of an Euler-Bernoulli beam of constant depth and with linearly varying breadth // Journal of Sound and Vibration. 1992. V. 153. pp. 509-522.

25. Zhou D., Cheung Y.K. Vibrations of tapered Timoshenko beams in terms of static Timoshenko beam functions // Journal of Applied Mechanics. 2001. V. 68. pp. 596-602.

26. Cranch E.T., Adler A. Bending vibrations of variable section beams // American Society of Mechanical Engineers. 1956. V. 23, № 1. pp. 103108.

27. Ece M.C., Aydogdu M., Taskin V. Vibration of a variable cross-section beam // Mechanics Research Communications. 2007. V. 34. pp. 78-84.

28. Eisenberger M. Exact longitudinal vibration frequencies of a variable cross-section rod // Applied Acoustics. 1991. V. 34. pp. 123-130.

29. Graf K. F. Wave Motion in Elastic Solids. Columbus, Ohio: Ohio State University Press, 1975. p. 641.

30. Conway H.D., Dubil J.F. Vibration frequencies of truncated wedge and cone beam // Journal of Applied Mechanics. 1965. V. 32, № 4. pp. 932- 935.

31. Mabie J.J., Rogers C.B. Transverse vibrations of double-tapered cantilever beams // Journal of Acoustical Society of America. 1972. V. 51. pp. 1771-1772.

32. Bayley P.B., Everitt W.N., Zettl A. Computing eigenvalues of singular Sturm-Liouville problems // Results in Mathematics. 1991. V. 20.

33. Carrera, E., Giunta, G., Nali, P., and Petrolo, M. (2010). Refined beam elements with arbitrary cross-section geometries. Computers and Structures, 88(5-6), 283-293.

34. Elishakoff, I. (2005). Eigenvalues of Inhomogeneous Structures: Unusual Closed-form Solutions. CRC Press, Boca Raton, FL.

35. Kostin, G.V. and Saurin, V. V. (2012). Integrodifferential relations in linear elasticity. De Gruyter, Berlin.

36. Kostin, G.V. and Saurin, V. V. (2017). Dynamics of solid structures. Method using integrodifferential relations. De Gruyter, Berlin.

37. Б.В.Гусев Строительная конструкция типа балки. Патент № 25620077, 07.08.2015.

Variational approaches to finding eigenvalues for beams with variable cross-section

Gusev B.V. , Saurin V.V.

Russian University of Transport» (RUT — MIIT)

The work consists of an introduction and eight sections. The introduction discusses the relevance of the problems associated with studying vibrations of inhomogeneous beams. The analysis of publications and obtained results in this field is performed. The second part is devoted to the formulation of the boundary value problem to finding natural frequencies of an inhomogeneous beam in the framework of the Euler-Bernoulli hypotheses. The next section deals with questions related to various classical variational formulations for the spectral problem arising in the beam theory. Particularities of the application of the direct and complementary Hamiltonian principles to such type of the boundary-value problems are discussed. The fourth section describes the method of integro-differential relations, which is an alternative to the classical variational approaches. Next, the possibilities to constructing various bilateral energy quality estimates for approximate solutions that follow from the method of integro-differential relations are investigated. In the sixth section the results obtained and discussed in the previous sections are generalized and an one-parameter family of quadratic nonnegative functionals whose stationarity conditions together with integro-differential constraints constitute a complete system of equations describing the dynamic behavior of non-homogeneous beams are introduced. In the seventh section, the relations of the variational problems obtained using the introduced family of functionals to the classical variational principles are considered. In the seventh and final part, based on a numerical model example, the advantages of the variational technique in problems of free vibrations of inhomogeneous beams are discussed.

Key words: dynamics, a beam with a variable cross-section, eigenvibrations, numerical methods, structural inhomogeneity, finite element method, functionally graded materials.

1. Rosa M.A. De, Auciello N.M. Free vibrations of tapered beams with flexible ends // Computers & Structures. 1996. V. 60, № 2. pp. 197-202.

2. Cranch E.T., Adler A. Bending vibrations of variable section

beams // American Society of Mechanical Engineers. 1956. V. 23, № 1. pp. 103-108.

3. Caruntu D.I. On nonlinear vibration of nonuniform beam with

rectangular cross-section and parabolic thickness variation // Solid Mechanics and its Applications. 2000. V. 73. pp. 109-118.

4. Chaudhari T.D., Maiti S.K. Modelling of transverse vibration of

beam of linearly variable depth with edge crack // Engineering Fracture Mechanics. 1999. V. 63. pp. 425-445.

5. Auciello N.M. On the transverse vibrations of non-uniform

beams with axial loads and elastically restrained ends // International Journal of Mechanical Sciences. 2001. V. 43. pp. 193-208.

6. Elishakoff I. Eigenvalues of Inhomogeneous Structures: Unusual Closed-form Solutions. Boca Raton, FL: CRC Press, 2005.

7. Hsu J.C., Lai H.Y., Chen C.K. Free vibration of non-uniform Euler-

Bernoulli beams with general elastically end constraints using Adomian modified decomposition method // Journal of Sound and Vibration. 2008. V. 318. pp. 965-981.

8. Franciosi C., Mecca M. Some finite elements for the static

analysis of beams with varying cross section // Computers and Structures. 1998. V. 69, № 2. pp. 191-196.

9. Jang S.K., Bert C.W. Free vibration of stepped beams: Exact

and numerical solutions // Journal of Sound and Vibration. 1989. V. 130. pp. 342-346.

10. Prediction of the influence of temperature field on the critical speeds of a rod-fastened rotor / S. Liu, Y. Zhang, Z. Du [and others.] // Gas Turbine Technology. 2011. V. 2. pp. 20-23.

11. Simsek M., Cansiz S. Dynamics of elastically connected double-functionally graded beam systems with different boundary conditions under action of a moving harmonic load // Composite Structures. 2012. V. 94, № 9. pp. 2861-2878.

12. Gorman D.J. Free vibration analysis of beams and shafts. New York: Wiley, 1975.

13. Rao S. Ramalingerswara, Ganesan N. Dynamic response of tapered composite beams using higher order shear deformation theory // Journal of Sound and Vibration. 1995. V. 187, № 5. pp. 737-756.