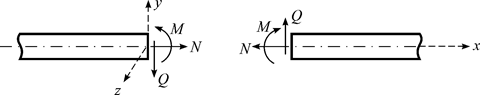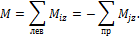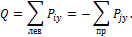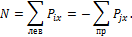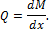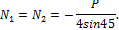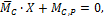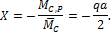Цели и задачи курсовых, контрольных работ
Собственные колебания системы с конечным числом степеней свободы
Рассмотрим балку (рис. 9.8) с n сосредоточенными массами, которые совершают собственные колебания в вертикальной плоскости. Вращения, горизонтальные смещения масс и силы сопротивления внешней среды при анализе колебательного процесса не учитываются.
Число степеней свободы такой системы равно n. К каждой из масс приложены силы инерции J1,J2,…, Jn. В этом случае имеют место собственные колебания системы с n степенями свободы.
Обозначим отклонение масс y1, y2,…, yn, а амплитуды колебаний — A1, A2,…, An.
Уравнения движения масс примем в виде, описанном выражениями
В соответствии с принятым законом колебаний (9.21) определим силы инерции:
sin( w t + n ) = m1 w 2y1;
J2 = — m2 sin( w t + n ) = m1 w 2y1;
Найдем перемещения точек прикрепления каждой из масс от всех инерционных сил:
Разделим в (9.23) все слагаемые на ω2 и, обозначая (собственное число), перенося все слагаемые в одну сторону, получим систему линейных однородных алгебраических уравнений, неизвестными в которых являются перемещения у точек прикрепления масс.
Система уравнений (9.24) имеет два решения. Первое: когда неизвестные (в данном случае у) равны 0. Такое решение не соответствует физике этой задачи, т.к. оно обозначает, что рассматриваемая балка находится в состоянии покоя. Второе: отличное от нуля, когда y1 0; y2 0; yn 0 и т.д. Но это решение возможно лишь в том случае, если ее определитель, составленный из коэффициентов при неизвестных, будет равен нулю.
Определитель, составленный из коэффициентов при неизвестных, представляет собой уравнение, которое называется характеристическим или вековым. Для определения корней λ1, λ2,…, λn этого уравнения каждому значению λi соответствует собственная частота колебаний . Число частот равно числу степеней свободы рассматриваемой системы. Покажем первые три формы колебаний для рассмотренной ранее балки (рис. 9.9).
= 0 — вековое уравнение. (9.25)
Свободные колебания систем могут происходить как по одной из форм колебаний, так и по совокупности нескольких форм. В рассмотренном решении не учтены силы сопротивления, что является приближенным решением. Для практических задач результаты приведенного расчета систем на собственные колебания являются приемлемыми с достаточной степенью точности. Каждой частоте ωi соответствует своя форма колебаний.
Собственные колебания систем с одной степенью свободы без учёта сил сопротивления внешней среды Рассмотрим невесомую балку, весом которой по сравнению с массой m пренебрегаем
Вынужденные колебания системы с одной степенью свободы
Расчет рамы на динамическое действие нагрузки Рассмотрим статически определимую раму, на горизонтальном элементе которой находятся колеблющиеся массы.
Основные уравнения строительной механики
Математическая сторона основной задачи строительной механики основана на зависимостях, полученных в сопромате. Напомним их на примере напряженно-деформированного состояния элемента рамы, для которого – в отличие от балки – поперечный изгиб сопровождается дополнительным растяжением или сжатием.
Пусть такой элемент длиной dx расположен в локальной системе координат Oxy, где ось Ox направлена по оси стержня, и загружен распределенной нагрузкой интенсивностью qx и qy вдоль Ox и Oy соответственно (рис. 1.20).
Напряженно-деформированное состояние стержня определяется девятью компонентами:
– деформациями (κ, g, e).
Уравнения для определения этих функций можно разделить на три группы.
Статические уравнения – связывают внутренние усилия (рис. 1.20, б) с заданной нагрузкой:
Геометрические уравнения – выражают деформации через перемещения, показанные на рис. 1.20, в, г:
Физические уравнения – представляют собой зависимости между внутренними усилиями и деформациями:
где E – модуль Юнга;
G – модуль сдвига;
F – площадь поперечного сечения стержня;
J – момент его инерции;
m – коэффициент, учитывающий неравномерность распределения касательных напряжений в поперечном сечении стержня.
| Q > 0 |
| γ>0 |
| Q+dQ |
| M > 0 |
| N+dN |
| qx > 0 |
| qy > 0 |
| u>0 |
| θ>0 |
| N > 0 |
| M+dM |
| θ+dθ > 0 |
Отметим, что выражения EJ и EF в (1.12) называются жесткостями стержня при изгибе и растяжении (сжатии) соответственно.
При решении системы уравнений (1.10) – (1.12) возможны два варианта:
1) внутренние усилия M, Q, N удается найти из системы уравнений (1.10), не обращаясь к остальным уравнениям – это СОС;
2) внутренние усилия можно найти только путем совместного решения всех девяти уравнений – это СНС.
В последнем случае при решении этих уравнений возможны два подхода:
– в качестве основных неизвестных выбирают усилия M, Q, N, выражая все остальные через них – это решение в форме метода сил;
– в качестве основных неизвестных выбирают перемещения u, v, q – это решение в форме метода перемещений.
Системы, описываемые линейными уравнениями (1.10) — (1.12), называются линейно-деформируемыми. Для них справедлив принцип суперпозиции, в соответствии с которым:
внутренние усилия, перемещения и деформации от заданной нагрузки (или иного воздействия) можно найти как сумму соответствующих величин от каждой нагрузки в отдельности.
Примечания
1. Первое из статических уравнений (1.10) получается из условия равновесия рассматриваемого элемента рамы. Полагая в его пределах qx = const, и составляя уравнение SX = 0, получим:
откуда и следует искомая зависимость. Два других уравнения из (1.10) – это дифференциальные зависимости Журавского.
2. Первое из физических уравнений (1.12) представляет собой дифференциальное уравнение изогнутой оси балки:
Второе уравнение в предпосылке равномерного распределения касательных напряжений в поперечном сечении стержня (m =1) выражает закон Гука при сдвиге:
При этом мы не уточняем смысл коэффициента m по причине, которая будет указана в § 3.5. Последнее из физических уравнений (1.12) – это закон Гука при ЦРС:
3. В дальнейшем мы будет по-прежнему применять обозначение Oxy для глобальной системы координат, связанной с конструкцией в целом.
Вековое уравнение строительная механика это
4. Статически определимые системы. Методы расчета статически определимых
систем на постоянную нагрузку
4.1. Статически определимые системы
Еcли чиcло ypавнений pавновеcия pавно чиcлy элементаpных cвязей cиcтемы С , включая опорные, то ycилия в этих cвязях можно однозначно опpеделить из этихypавнений. Для этого необходимо, чтобы чи c ло cвязей C было pавно в плоcкой cиcтеме 3D, а в пpоcтpанcтвенной — 6Б, так как общее чиcло cтепеней cвободы cиcтемы cжеcткими элементами и cвязями:
n = 3D — C (в пло c кой cиcтеме);
n = 6Б — C (в п p оcтpанcтвенной cиcтеме).
Оп p еделенное таким обpазом чиcло cтепеней cвободы cиcтемы называетcя cтепенью или числом геометрической изменяемоcти cиcтемы. Реальные c иcтемыдолжны быть неизменяемыми, т.е. обладать нyлевой или отpицательной cтепенью изменяемоcти.
Статически определимой называется система, внутренние усилия которой можно определить только из уравнений статики (равновесия).
Статически определимые системы (СОС) имеют свои особенности:
1) их внутренние усилия не зависят от упругих характеристик материала, форм сечений и площадей элементов;
2) воздействие температуры, осадки опор, неточность изготовления элементов не вызывают внутренних усилий;
3) если нет внешних нагрузок, все внутренние усилия равны нулю;
4) замена нагрузки на одном из дисков статически ей эквивалентной не приводит к изменению усилий в остальной части системы;
5) изменение конфигурации какого-либо диска при сохранении связей его с остальной частью системы и с основанием не вызывает усилий в остальной части системы;
6) нагрузка, приложенная к основной части стержневой системы, не вызывает усилий в прикрепленных частях, но загружение прикрепленных частей приводит к возникновению внутренних усилий и в основной части сооружения.
C иcтемы c одной cтепенью изменяемоcти называютcя механизмами ; c неcколькими cтепенями изменяемоcти — кинематичеcкими цепями . C иcтемы c нyлевойcтепенью изменяемоcти называютcя cтатичеcки опpеделимыми .
Итак, в c татичеcки опpеделимых cиcтемах n = 0. Заметим, что n = 0 для систем, находящихся в равновесном состоянии, является необходимым, а n = 0 и W = 0 необходимым и достаточным условием статической определимости и геометрической неизменяемости системы. По c колькy ypавнения pавновеcия вcегда линейные, то дляопpеделения внyтpенних cил в cтатичеcки опpеделимых cиcтемах можно пользоватьcя пpинципом незавиcимоcти дейcтвия cил. В c татичеcки опpеделимых cиcтемах значения усилий можно однозначно определить методом сечений с применением уравнений равновесия статики.
Статиче c ки опpеделимые cиcтемы имеют и cвои недоcтатки, главным из котоpых являетcя отcyтcтвие pезеpвиpования. В c лyчае pазpyшения одного из элементов заданной системы, она превращается в геометрически изменяемую. Данное обстоятельство снижает надежно c ть и безопаcноcть статически определимых систем в эксплуатационных режимах. В этом отношении п p еимyщеcтво имеют cиcтемы c “лишними” cвязями, т.е. c отpицательной cтепенью изменяемоcти, полyчившие названиеcтатичеcки неопpеделимых cиcтем.
4.2. Методы расчета статически определимых
систем на постоянную нагрузку
Важной задачей расчета сооружений является определение их напряженно-деформированного состояния (НДС). Эта задача состоит из :
– определения опорных реакций и внутренних усилий;
– определения перемещений и деформаций.
Перед расчетом должны быть установлены геометрические размеры и формы элементов сооружения, физические характеристики материала, внешняя нагрузка и особенности ее воздействия.
Наиболее простым является расчет статически определимых систем.
4.2.1. Определение опорных реакций
Сооружение, воспринимая внешнюю нагрузку, через свои элементы передает ее опорам, вызывая в них опорные реакции.
При определении опорных реакций используется принцип освобождения от связей : всякое тело можно освободить от связей, заменив их реакциями. После этого из уравнений равновесия можно определять величины опорных реакций.
Уравнения равновесия плоской системы записываются в трех формах:
( Σ X и Σ Y – суммы проекций на взаимно-пересекающиеся оси x и y , Σ M A – сумма моментов всех сил относительно любой точки A на плоскости);
(точки A и B не должны лежать на одном перпендикуляре к оси x );
(точки А , В, С не должны лежать на одной прямой).
4.2.2. Внутренние усилия стержневой системы
В элементах плоской стержневой системы возникают три усилия: продольная сила N, поперечная сила Q , изгибающий момент M . Для любого поперечного сечения стержня они определяются как на рис. 4.1.
Изгибающий момент – это сумма моментов всех сил, лежащих слева (или справа) от сечения относительно оси z :
В строительной механике знак изгибающего момента обычно не устанавливается, а эпюра M изображается на стороне растянутого волокна.
Поперечная сила – это сумма проекций на ось y всех сил, лежащих слева (или справа) от сечения:
Поперечная сила положительна, если вращает элемент по часовой стрелке, и отрицательна, если вращает его против часовой стрелки.
Продольная сила – это сумма проекций всех сил на ось x , лежащих слева (или справа) от сечения:
Продольная сила положительна, если растягивает элемент, и отрицательна, если сжимает его.
Между M и Q существует дифференциальная зависимость:
Исходя из геометрического смысла первой производной, величина Q равняется тангенсу угла между осью эпюры M и касательной к ней.
По эпюре M можно определить знак Q. Для этого ось эпюры M нужно повернуть до совпадения с касательной к ней. Если поворот будет по часовой стрелке, Q будет со знаком «+», а если против часовой стрелки, то со знаком « –» .
Эпюры поперечных и продольных сил можно изображать на любой стороне от оси стержня, но эпюру изгибающего момента нужно обязательно изображать на стороне растянутого волокна.
4.3. Методы определения внутренних усилий
Внутренние усилия статически определимых систем определяются методами простых сечений, совместных сечений, вырезания узла, замены связей и др.
4.3.1. Метод простых сечений
Этот метод позволяет рассматривать внутреннее усилие как внешнюю силу и определять его из уравнений статики (равновесия).
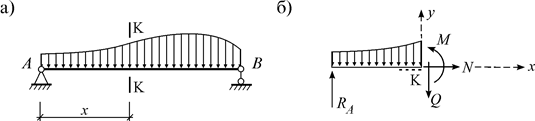
Например, внутренние усилия балки (рис. 4.2, а) в сечении К определяются как на рис. 4.2, б.
Алгоритм метода простых сечений :
1) поделить систему на участки;
2) выбрать участок и провести поперечное сечение;
3) выбрать одну (наиболее простую) из отсеченных частей;
4) составить три уравнения равновесия;
5) из них определить внутренние усилия M, Q, N ;
6) для данного участка построить эпюры M, Q, N ;
7) повторить пункты 2-6 для остальных участков.
4.3.2. Метод совместных сечений
Этот метод используется при расчете многодисковых систем.
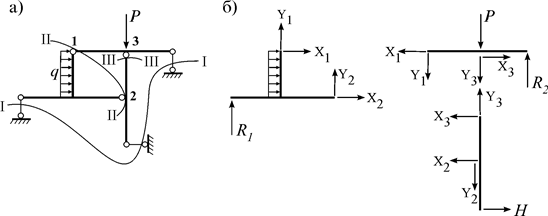
Например, для расчета трехдисковой рамы (рис. 4.3, а) проводятся три совместных сечения I, II, III . В результате выявляются девять неизвестных реакций (рис. 4.3, б): опорные реакции R1, R2, H и междисковые реакции X1, X2, X3, Y1, Y2, Y3 . Составив для каждого диска по три уравнения равновесия, т.е. 3 × 3=9 уравнений, из их решения определяются все 9 реакций.
Алгоритм метода совместных сечений :
1) совместными сечениями разделить систему на части (диски);
2) обозначить опорные и междисковые реакции;
3) для каждого диска записать уравнения равновесия;
4) решить систему полученных уравнений;
5) каждый диск рассчитать отдельно и построить эпюры;
6) объединить все эпюры в общие эпюры M, Q, N .
4.3.3. Метод вырезания узла
Используется для определения усилий простых систем.
Сущность метода: вырезается узел с не более чем двумя неизвестными усилиями; силы, действующие в узле, проецируются на две оси; из этих уравнений определяются искомые усилия.
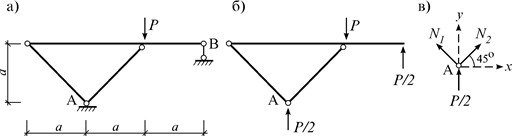
Например, при расчете балочно-ферменной системы (рис. 4.4, а), после того как определены опорные реакции (рис. 4.4, б), вырезается узел А (рис. 4.4, в) и составляются уравнения равновесия:
Из них определяются искомые продольные силы:
4.3.4. Метод замены связей
Используется при расчете сложных статически определимых систем, которые трудно рассчитать другими способами.
Сущность метода : сложная система превращается в более простую путем перестановки связи (или нескольких связей) в другое место; из условия эквивалентности заданной и заменяющей систем определяется усилие в переставленной связи; затем система рассчитывается известными способами.
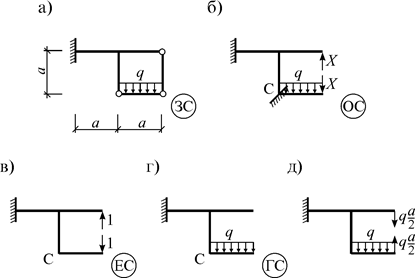
Например, для расчета рамы (рис. 4.5? а) удалим правый вертикальный стержень заданной системы (ЗС) и введем одну связь в левый шарнир. Тогда шарнир станет припайкой С , а примыкающие к нему стержни будут жестко связаны. Обозначив усилие в удаленной связи через X , получим так называемую основную систему (ОС) для расчета рамы (рис. 4.5? б).
Условием эквивалентности ОС по отношению к ЗС будет условие равенства нулю момента в точке С : MC =0. По принципу суперпозиции этот момент равняется сумме моментов от силы X и внешней нагрузки:
Теперь рассмотрим два состояния ОС:
1) единичное состояние (ЕС), где прикладываются силы X =1 (рис. 4.5, в);
2) грузовое состояние (ГС), где прикладывается нагрузка (рис. 4.5, г).
Тогда предыдущее уравнение примет вид
где 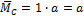
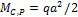
Теперь неизвестное усилие легко вычисляется:
После этого можно перейти к расчету более простой системы (рис. 4.5, д).
В более сложных случаях переставляются несколько связей и записываются столько же условий эквивалентности:
Здесь 1, 2, …, n – заменяемые связи; X1, X2, …, Xn – неизвестные внутренние усилия в этих связях; sij – усилие в связи i в j- ом единичном состоянии; SiP – усилие в i- ой связи в грузовом состоянии.
Из этой системы уравнений определяются неизвестные X1, X2, …, Xn .
Общий вывод. Расчет любой статически определимой системы приводит к решению системы n линейных уравнений с n неизвестными. Если определитель полученной системы уравнений отличен от нуля (det ≠ 0), внутренние усилия будут конечными величинами. Если же определитель равняется нулю (det=0), то внутренние усилия определить нельзя. В этом случае система является мгновенно изменяемой.
http://lektsii.org/8-86346.html
http://mathenglish.ru/mechanics/sm0/lect4.htm