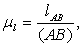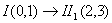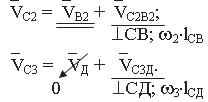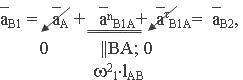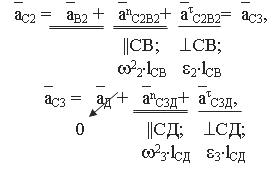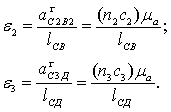Векторное уравнение для определения скорости

Векторные формулы для скоростей и ускорений точек тела

Векторные формулы для скоростей и ускорений точек тела

• Представляет скорость, касательную, нормальную и общую скорость тела POINT в формате VECTOR. Точка на модуле относительно направления может быть выражена как векторное произведение (14) Где r — радиус-вектор точки M и задается произвольной заточкой оси вращения Oz, например, точкой O (рис. 35). Уравнение (14) называется векторным уравнением Эйлера. Проверьте, чтобы проверить выражение. Фактически вектор W x G перпендикулярен следующей плоскости. болезнь Рисунок 35.

Поэтому необходимо интегрировать линейные дифференциальные уравнения, соответствующие второму этапу, используя координаты первого этапа и конечное значение скорости в качестве начального условия движения. Людмила Фирмаль

Вектор, содержащийся в векторном произведении. Направление параллельно скорости V вдоль тангенса круга. Модуль векторного производства 2. (16) В справедливости (16) мы убеждены рассчитать их правильную часть. У нас есть ex r | = ersin (s, r) = eh, Это согласуется с тангенциальным ускорением. Направление сектора ххг параллельно вектору тангенциального ускорения (рис. 36). На векторное произведение W x V w x v | = wnsin (w, v) = wi> = hw2 = a „, Это потому, что векторы w и V перпендикулярны друг другу. Направление вектора W x V параллельное N0 векторное регулярное выражение и упорядочение от точки M к оси вращения POET „= — ой w2.

• При корректировке вектора h в направлении от оси вращения. Справедливость уравнения (16) установлена. Из определения точечной скорости неизвестно V = dr / dz, Где r — радиус фиксированной точки, особенно точки, нарисованной из любой точки на оси вращения объекта, который вращается вокруг фиксированной оси. Однако скорость точности вращательного движения тела определяется векторной формулой Эйлера (Сравнение двух уравнений для скорости точки дает уравнение для вычисления производной по времени от вектора r. dr / dr = wxr. (17).

Действующая сила определяет только ускорение точки движения, а скорость и положение точки на траектории могут зависеть от скорости и начального положения точки, сообщенной в точке первого мгновения. Людмила Фирмаль

В этом выражении вектор r всегда имеет постоянный модуль, потому что он соединяет две точки сплошного модуля. Вектор

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Вектор скорости и ускорения материальной точки и их модули. Пример решения задач.

В очередной раз меня попросили решить пару задачек по физике, и я вдруг обнаружил, что не могу решить их с ходу. Немного погуглив, я обнаружил, что сайты в топе выдачи содержат сканы одного и того же учебника и не описывают конкретных примеров решений задачи о том, как найти вектор скорости и ускорения материальной точки. По-этому я решил поделиться с миром примером своего решения.

Траектория движения материальной точки через радиус-вектор

Подзабыв этот раздел математики, в моей памяти уравнения движения материальной точки всегда представлялись при помощи знакомой всем нам зависимости y(x) , и взглянув на текст задачи, я немного опешил когда увидел векторы. Оказалось, что существует представление траектории материальной точки при помощи радиус-вектора – вектора, задающего положение точки в пространстве относительно некоторой заранее фиксированной точки, называемой началом координат.

Формула траектория движения материальной точки помимо радиус-вектора описывается так же ортами – единичными векторами i, j , k в нашем случае совпадающими с осями системы координат. И, наконец, рассмотрим пример уравнения траектории материальной точки (в двумерном пространстве):

Что интересного в данном примере? Траектория движения точки задается синусами и косинусами, как вы думаете, как будет выглядеть график в всем нам знакомом представлении y(x) ? “Наверное какой-то жуткий”, подумали вы, но все не так сложно как кажется! Попробуем построить траекторию движения материальной точки y(x), если она движется по представленному выше закону:

Здесь я заметил квадрат косинуса, если вы в каком-нибудь примере видите квадрат синуса или косинуса, это значит что нужно применять основное тригонометрическое тождество, что я и сделал (вторая формула) и преобразовал формулу координаты y, чтобы вместо синуса подставить в нее формулу изменения x:

В итоге жуткий закон движения точки оказался обычной параболой, ветви которой направлены вниз. Надеюсь, вы поняли примерный алгоритм построения зависимости y(x) из представления движения через радиус-вектор. Теперь перейдем к нашему главному вопросу: как же найти вектор скорости и ускорения материальной точки, а так же их модули.

Вектор скорости материальной точки

Всем известно, что скорость материальной точки – это величина пройденного пути точкой за единицу времени, то есть производная от формулы закона движения. Чтобы найти вектор скорости нужно взять производную по времени. Давайте рассмотрим конкретный пример нахождения вектора скорости.

Пример нахождения вектора скорости

Имеем закон перемещения материальной точки:

Теперь нужно взять производную от этого многочлена, если вы забыли как это делается, то вот вам таблица производных различных функций. В итоге вектор скорости будет иметь следующий вид:

Все оказалось проще, чем вы думали, теперь найдем вектор ускорения материальной точки по тому же самому закону, представленному выше.

Как найти вектор ускорения материальной точки

Вектор ускорения точки это векторная величина, характеризующая изменение с течением времени модуля и направления скорости точки. Чтобы найти вектор ускорения материальной точки в нашем примере, нужно взять производную, но уже от формулы вектора скорости, представленной чуть выше:

Модуль вектора скорости точки

Теперь найдем модуль вектора скорости материальной точки. Как вы знаете из 9-го класса, модуль вектора – это его длина, в прямоугольных декартовых координатах равна квадратному корню из суммы квадратов его координат. И откуда же из полученного нами выше вектора скорости взять его координаты спросите вы? Все очень просто:

Теперь достаточно только подставить время, указанное в задаче и получить конкретное числовое значение.

Модуль вектора ускорения

Как вы поняли из написанного выше (и из 9-го класса), нахождение модуля вектора ускорения происходит тем же образом, что и модуля вектора скорости: извлекаем корень квадратный из суммы квадратов координат вектора, все просто! Ну и вот вам, конечно же, пример:

Как вы видите, ускорение материальной точки по заданному выше закону не зависит от времени и имеет постоянную величину и направление.

Еще примеры решений задачи нахождения вектора скорости и ускорения

А вот тут вы можете найти примеры решения и других задач по физике на тему “механика твердых тел”. А для тех, кто не совсем понял как найти вектор скорости и ускорения, вот вам еще парочка примеров из сети без всяких лишних объяснений, надеюсь, они вам помогут.

Если у вас возникли какие-нибудь вопросы, вы можете задать их в комментариях.

Векторное уравнение для определения скорости

Кинематический анализ механизмов по моделям

Цель работы: определение кинематических характеристик механизмов методом построения планов скоростей и ускорений.

Задачей кинематического анализа является определение линейных скоростей и ускорений точек звеньев и угловых скоростей и ускорении всех звеньев графо–аналитическим методом, т.е. методом построения планов скоростей и ускорений.

Планы скоростей и ускорений имеют следующие свойства:

1) В полюсе плана скоростей (ускорений) линейные скорости (ускорения) равны нулю.

2) Лучи, проведенные из полюса плана скоростей (ускорений) до соответствующих точек, обозначают абсолютные линейные скорости (ускорения) аналогичных точек звеньев механизмов в выбранном масштабе.

3) Отрезки, соединяющие концы лучей, соответствуют относительным скоростям (ускорениям) соответствующих точек звеньев в принятом масштабе.

4) Отрезки прямых, соединяющих точки на схеме механизма, и отрезки прямых, соединяющих концы векторов скоростей (ускорений) этих точек, образуют подобные сходственно расположенные фигуры.

5) Направление угловых скоростей (ускорений) определяются направлением возможности поворота звена на схеме механизма вектором относительной скорости (ускорения) плана скоростей (ускорений), приложенным к соответствующей точке звена механизма.

6) Концы векторов абсолютных скоростей (ускорений) на планах скоростей (ускорений) обозначаются теми же буквами латинского алфавита (но строчными), что и соответствующие точки на плане механизма. Например, для механизма, изображенного на рисунке 1 на плане скоростей вектор ab соответствует звену плана механизма AВ и обозначает относительную скорость точки В относительно точки А звена АВ.

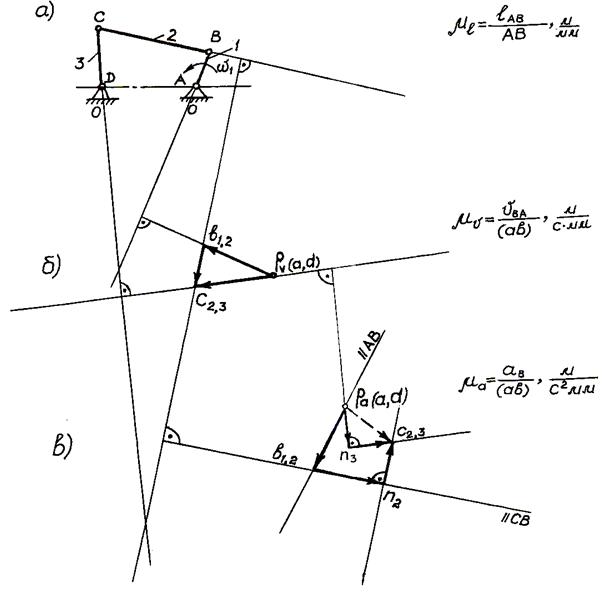
Рассмотрим пример построения планов скоростей и ускорений для механизма, представленного на рисунке 1. План механизма построен в масштабе, причем масштабный коэффициент длины равен

где l _AB – истинная длина звена АВ, м;

( АВ) – длина отрезка АВ в мм, взятая из плана механизма;

– масштабный коэффициент, м /мм –1 .

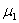
Угловая скорость ведущего звена постоянная, т.е. 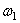= const .

Последовательность кинематического анализа определяется формулой строения механизма, полученной в результате структурного анализа. Формула строения рассматриваемого механизма

Кинематический анализ необходимо начинать с ведущего звена со стойкой (механизма I класса), затем переходить к кинематическому анализу групп Ассура второго класса первого вида II ₁ (2, 3), состоящей из 2 и 3 звеньев.

Для построения плана скоростей (ускорений) необходимо графически решить векторные уравнения:

1) Рассмотрим механизм первого класса I (О, 1), запишем векторное уравнение для определения скорости точки В звена 1, т.е.

,

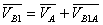
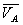
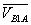
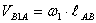
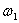
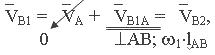
где -вектор скорости точки А , скорость точки А равна 0;

– вектор относительной скорости точки В₁ относительно точки А , причем , направлена по перпендикуляру к ( АВ) в сторону . Все это удобно записать так:

,

так как скорость точки В₁ и точки В₂, входящих во вращательную пару В, равны.

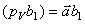
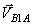
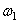
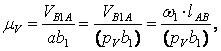
2) Выбираем полюс плана скоростей (точка р _V ), решаем векторное уравнение графически. Так как скорость точки А, принадлежащей стойке О, равна нулю, то точка А звена 1 будет находиться в полюсе плана скоростей и будет обозначена буквой (а). Из полюса (р _V ) откладываем вектор , изображающий на плане скоростей вектор скорости , он перпендикулярен звену АВ и направлен в сторону вращения . Выбрав длину отрезка (р _V b ₁ ), определяем масштабный коэффициент плана скоростей:

мс –1 мм –1 .

3) Рассмотрим группу Ассура II ₁ (2,3). Определим скорость точки С, принадлежащая звену 2 и звену 3, которые образуют кинематическую вращательную пару С, а поэтому

.

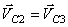
Запишем два векторных уравнения и решим их графически:

На плане скоростей из конца вектора ( ab ₂ ) проводим направление вектора скорости ` 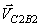перпендикулярно звену 2.

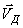
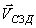
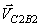
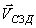
Из полюса, где находится точка Д звена 3, так как ` равна нуля, проводим направление вектора скорости ` перпендикулярно звену СД. Пересечения векторов ` и ` даст на плане скоростей точку с_2,3, принадлежащую точке С механизма. План скоростей представлен на рисунке 1.

4) Определим величину угловых ускорений звеньев 2 и 3. Из векторных уравнений имеем:

с –1 ;

с –1 ;

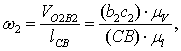
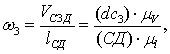
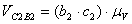
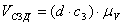
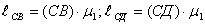
так как из плана скоростей , ; а из плана механизма .

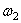
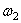
5) Определим направление угловых скоростей звеньев 2 и 3. Направление угловых скоростей определяется по направлению векторов относительных скоростей соответствующих точек звена. Например, направление определяется направлением вектора ( b ₂ c ₂ ), вектор ( b ₂ c ₂ ) из плана скоростей условно переносим в точку С звена СВ, если вектор ( b ₂ c ₂ ) поворачивает звено СВ вокруг точки В против часовой стрелки, то и направление угловой скорости – против часовой стрелки как это показано на рисунке 2.

Рассмотрим построение плана ускорений.

Записываем и решаем векторные уравнения в той же последовательности, что и при построении плана скоростей, т.е.

так как точки В₁ и В₂ образуют вращательную пару В,

где а _A – ускорение точки А равно нулю, т.к. точка А принадлежит стойке;

– нормальное (центростремительное) ускорение, направленное к «центру», т.е. к точке А , параллельно АВ;

– тангенциальное (касательное) ускорение равно нулю, т.к. по условию задачи , значит, равно нулю и угловое ускорение ведущего звена.

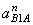
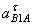
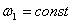
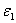
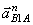
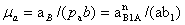
Выбираем полюс плана ускорений (точка р_а). Ускорение точки А равно нулю, значит, точка А будет в полюсе плана ускорений (точка а). Из полюса (р_а) откладываем отрезок ( а b _1,2 ) = ( p_a b _1,2 ), изображающий на плане ускорений вектор ускорения , он параллелен звену ВА и направлен к центру вращения (точке А). Масштабный коэффициент равен , м × с –2 мм –1 .

6) Рассмотрим группу Ассура, запишем векторные уравнения:

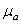
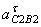
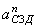
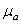
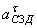
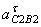
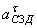
Из конца вектора ( ab _1,2 ) плана ускорений проводим вектор ( b ₂ n ₂ ), соответствующий в масштабе вектору нормального ускорения а n _С2В2 параллельно звену СВ в направлении к центру вращения (точка В), из конца вектора ( b ₂ n ₂ ) проводим перпендикулярно ( b ₂ n ₂ ) направление вектора тангенциального ускорения , величина которого пока неизвестна. Из полюса проводим параллельно звену СД в направлении к центру вращения (точка Д) вектор центростремительного ускорения , величина которого известна, в масштабе ; затем из конца вектора ( an ₃ ) проводим перпендикуляр, соответствующий касательному ускорению . Линии векторов, соответствующих тангенциальным ускорениям и пересекутся, на их пересечении будет находится точка с_2,3, соответствующая точке С на плане механизма. Соединяем точку с_2,3 с полюсом (р_а) плана ускорений.

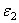
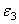
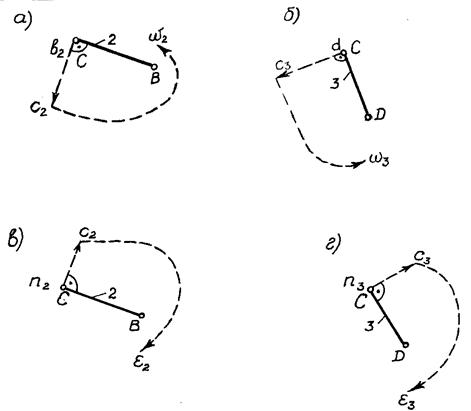
7) Из уравнений ускорений определяем величину угловых ускорений звеньев 2 и 3, т.е. и ;

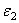
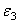
Определение направлений угловых ускорений и показано на рисунке 2.

По плану скоростей можно найти скорость любой точки механизма, например, .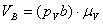

Из плана ускорений можно найти величину полного, тангенциального или центростремительного ускорения любой точки механизма, например, .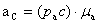

Рисунок 1 – План скоростей и ускорений

а) кинематическая схема механизма; б) план скоростей; в) план ускорений

Рисунок 2 – Определение направлений угловых скоростей и угловых ускорений

Порядок выполнения работы

1. Построить кинематическую схему механизма (план механизма в масштабе 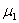) по модели, структурный анализ которого выполнен в лабораторной работе №3. Написать формулу строения механизма.

2. Построить план скоростей в масштабе .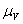

3. Определить по величине из плана скоростей скорости всех точек механизма.

4. Определить величину и направление угловых скоростей звеньев механизма.

5. Построить план ускорений в масштабе .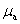

6. Определить полные ускорения всех точек механизма из плана ускорений.

7. Определить величину и направление угловых ускорений звеньев механизма.

Основные правила техники безопасности

1. Соблюдать осторожность при проведении лабораторной работы, чтобы не вывести из строя модели механизмов.

2. Тип, номер и наименование модели.

3. План механизма в масштабе.

4. План скоростей и план ускорений, построенные в масштабе.

5. Определение величин скоростей точек механизма по построенному плану скоростей.

6. Определение величин ускорений точек механизма по плану ускорений.

7. Определение величин и направлений угловых скоростей и ускорений звеньев механизма (с указанием направлений на звеньях механизма).

1. Что называется планом скоростей (ускорений)?

2. Чем определяется последовательность кинематического анализа механизма?

3. Какими буквами латинского алфавита принято обозначать точки на плане механизма, на планах скоростей и ускорений?

4. Как вычисляется масштабный коэффициент длины (скорости, ускорения)?

5. Как по планам скоростей и ускорений найти величину скоростей и ускорений точек механизма?

6. Как по плану скоростей (ускорений) найти направление угловых скоростей (угловых ускорений) звеньев механизма?

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21