Векторное уравнение для скоростей на

Векторные формулы для скоростей и ускорений точек тела

Векторные формулы для скоростей и ускорений точек тела

• Представляет скорость, касательную, нормальную и общую скорость тела POINT в формате VECTOR. Точка на модуле относительно направления может быть выражена как векторное произведение (14) Где r — радиус-вектор точки M и задается произвольной заточкой оси вращения Oz, например, точкой O (рис. 35). Уравнение (14) называется векторным уравнением Эйлера. Проверьте, чтобы проверить выражение. Фактически вектор W x G перпендикулярен следующей плоскости. болезнь Рисунок 35.

Поэтому необходимо интегрировать линейные дифференциальные уравнения, соответствующие второму этапу, используя координаты первого этапа и конечное значение скорости в качестве начального условия движения. Людмила Фирмаль

Вектор, содержащийся в векторном произведении. Направление параллельно скорости V вдоль тангенса круга. Модуль векторного производства 2. (16) В справедливости (16) мы убеждены рассчитать их правильную часть. У нас есть ex r | = ersin (s, r) = eh, Это согласуется с тангенциальным ускорением. Направление сектора ххг параллельно вектору тангенциального ускорения (рис. 36). На векторное произведение W x V w x v | = wnsin (w, v) = wi> = hw2 = a „, Это потому, что векторы w и V перпендикулярны друг другу. Направление вектора W x V параллельное N0 векторное регулярное выражение и упорядочение от точки M к оси вращения POET „= — ой w2.

• При корректировке вектора h в направлении от оси вращения. Справедливость уравнения (16) установлена. Из определения точечной скорости неизвестно V = dr / dz, Где r — радиус фиксированной точки, особенно точки, нарисованной из любой точки на оси вращения объекта, который вращается вокруг фиксированной оси. Однако скорость точности вращательного движения тела определяется векторной формулой Эйлера (Сравнение двух уравнений для скорости точки дает уравнение для вычисления производной по времени от вектора r. dr / dr = wxr. (17).

Действующая сила определяет только ускорение точки движения, а скорость и положение точки на траектории могут зависеть от скорости и начального положения точки, сообщенной в точке первого мгновения. Людмила Фирмаль

В этом выражении вектор r всегда имеет постоянный модуль, потому что он соединяет две точки сплошного модуля. Вектор

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Вектор скорости и ускорения материальной точки и их модули. Пример решения задач.

В очередной раз меня попросили решить пару задачек по физике, и я вдруг обнаружил, что не могу решить их с ходу. Немного погуглив, я обнаружил, что сайты в топе выдачи содержат сканы одного и того же учебника и не описывают конкретных примеров решений задачи о том, как найти вектор скорости и ускорения материальной точки. По-этому я решил поделиться с миром примером своего решения.

Траектория движения материальной точки через радиус-вектор

Подзабыв этот раздел математики, в моей памяти уравнения движения материальной точки всегда представлялись при помощи знакомой всем нам зависимости y(x) , и взглянув на текст задачи, я немного опешил когда увидел векторы. Оказалось, что существует представление траектории материальной точки при помощи радиус-вектора – вектора, задающего положение точки в пространстве относительно некоторой заранее фиксированной точки, называемой началом координат.

Формула траектория движения материальной точки помимо радиус-вектора описывается так же ортами – единичными векторами i, j , k в нашем случае совпадающими с осями системы координат. И, наконец, рассмотрим пример уравнения траектории материальной точки (в двумерном пространстве):

Что интересного в данном примере? Траектория движения точки задается синусами и косинусами, как вы думаете, как будет выглядеть график в всем нам знакомом представлении y(x) ? “Наверное какой-то жуткий”, подумали вы, но все не так сложно как кажется! Попробуем построить траекторию движения материальной точки y(x), если она движется по представленному выше закону:

Здесь я заметил квадрат косинуса, если вы в каком-нибудь примере видите квадрат синуса или косинуса, это значит что нужно применять основное тригонометрическое тождество, что я и сделал (вторая формула) и преобразовал формулу координаты y, чтобы вместо синуса подставить в нее формулу изменения x:

В итоге жуткий закон движения точки оказался обычной параболой, ветви которой направлены вниз. Надеюсь, вы поняли примерный алгоритм построения зависимости y(x) из представления движения через радиус-вектор. Теперь перейдем к нашему главному вопросу: как же найти вектор скорости и ускорения материальной точки, а так же их модули.

Вектор скорости материальной точки

Всем известно, что скорость материальной точки – это величина пройденного пути точкой за единицу времени, то есть производная от формулы закона движения. Чтобы найти вектор скорости нужно взять производную по времени. Давайте рассмотрим конкретный пример нахождения вектора скорости.

Пример нахождения вектора скорости

Имеем закон перемещения материальной точки:

Теперь нужно взять производную от этого многочлена, если вы забыли как это делается, то вот вам таблица производных различных функций. В итоге вектор скорости будет иметь следующий вид:

Все оказалось проще, чем вы думали, теперь найдем вектор ускорения материальной точки по тому же самому закону, представленному выше.

Как найти вектор ускорения материальной точки

Вектор ускорения точки это векторная величина, характеризующая изменение с течением времени модуля и направления скорости точки. Чтобы найти вектор ускорения материальной точки в нашем примере, нужно взять производную, но уже от формулы вектора скорости, представленной чуть выше:

Модуль вектора скорости точки

Теперь найдем модуль вектора скорости материальной точки. Как вы знаете из 9-го класса, модуль вектора – это его длина, в прямоугольных декартовых координатах равна квадратному корню из суммы квадратов его координат. И откуда же из полученного нами выше вектора скорости взять его координаты спросите вы? Все очень просто:

Теперь достаточно только подставить время, указанное в задаче и получить конкретное числовое значение.

Модуль вектора ускорения

Как вы поняли из написанного выше (и из 9-го класса), нахождение модуля вектора ускорения происходит тем же образом, что и модуля вектора скорости: извлекаем корень квадратный из суммы квадратов координат вектора, все просто! Ну и вот вам, конечно же, пример:

Как вы видите, ускорение материальной точки по заданному выше закону не зависит от времени и имеет постоянную величину и направление.

Еще примеры решений задачи нахождения вектора скорости и ускорения

А вот тут вы можете найти примеры решения и других задач по физике на тему “механика твердых тел”. А для тех, кто не совсем понял как найти вектор скорости и ускорения, вот вам еще парочка примеров из сети без всяких лишних объяснений, надеюсь, они вам помогут.

Если у вас возникли какие-нибудь вопросы, вы можете задать их в комментариях.

Кинематика материальной точки

Основные формулы кинематики материальной точки

Приведем основные формулы кинематики материальной точки. После чего дадим их вывод и изложение теории.

Радиус-вектор материальной точки M в прямоугольной системе координат Oxyz :
,
где – единичные векторы (орты) в направлении осей x, y, z .

Скорость точки:
;
;
;
Единичный вектор в направлении касательной к траектории точки:
.
Вектор можно выбрать двумя способами во взаимно противоположных направлениях. Обычно его выбирают в направлении увеличения дуговой координаты. Тогда, наряду с модулем скорости , вводят алгебраическую величину скорости . При , вектор скорости сонаправлен с . При – имеет противоположное с направление.

Скорость и ускорение точки M

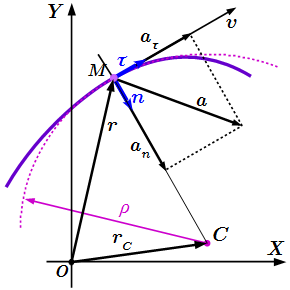
Тангенциальное (касательное) ускорение:
;
;
.
Здесь, как и для скорости, – это алгебраическое касательное ускорение, . Если , то вектор касательного ускорения сонаправлен с . При – имеет противоположное с направление.

Единичный вектор, направленный к центру кривизны траектории точки (вдоль главной нормали):
.

Радиус кривизны траектории:
.

Далее приводится вывод этих формул и изложение теории кинематики материальной точки.

Радиус-вектор и траектория точки

Рассмотрим движение материальной точки M . Выберем неподвижную прямоугольную систему координат Oxyz с центром в некоторой неподвижной точке O . Тогда положение точки M однозначно определяются ее координатами ( x, y, z ) . Эти координаты являются компонентами радиус-вектора материальной точки.

Радиус-вектор точки M – это вектор , проведенный из начала неподвижной системы координат O в точку M .
,
где – единичные векторы в направлении осей x, y, z .

При движении точки, координаты изменяются со временем . То есть они являются функциями от времени . Тогда систему уравнений
(1)
можно рассматривать как уравнение кривой, заданной параметрическими уравнениями. Такая кривая является траекторией точки.

Траектория материальной точки – это линия, вдоль которой происходит движение точки.

Если движение точки происходит в плоскости, то можно выбрать оси и системы координат так, чтобы они лежали в этой плоскости. Тогда траектория определяется двумя уравнениями

В некоторых случаях, из этих уравнений можно исключить время . Тогда уравнение траектории будет иметь зависимость вида:
,
где – некоторая функция. Эта зависимость содержит только переменные и . Она не содержит параметр .

Скорость материальной точки

Согласно определению скорости и определению производной:

Производные по времени, в механике, обозначают точкой над символом. Подставим сюда выражение для радиус-вектора:
,
где мы явно обозначили зависимость координат от времени. Получаем:

,
где
,
,

– проекции скорости на оси координат. Они получаются дифференцированием по времени компонент радиус-вектора
.

Таким образом
.
Модуль скорости:
.

Касательная к траектории

С математической точки зрения, систему уравнений (1) можно рассматривать как уравнение линии (кривой), заданной параметрическими уравнениями. Время , при таком рассмотрении, играет роль параметра. Из курса математического анализа известно, что направляющий вектор для касательной к этой кривой имеет компоненты:
.
Но это есть компоненты вектора скорости точки. То есть скорость материальной точки направлена по касательной к траектории.

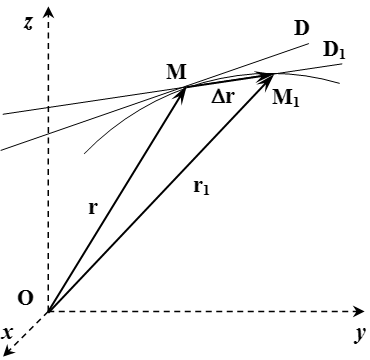
Все это можно продемонстрировать непосредственно. Пусть в момент времени точка находится в положении с радиус-вектором (см. рисунок). А в момент времени – в положении с радиус-вектором . Через точки и проведем прямую . По определению, касательная – это такая прямая , к которой стремится прямая при .
Введем обозначения:
;
;
.
Тогда вектор направлен вдоль прямой .

При стремлении , прямая стремится к касательной , а вектор – к скорости точки в момент времени :
.
Поскольку вектор направлен вдоль прямой , а прямая при , то вектор скорости направлен вдоль касательной .
То есть вектор скорости материальной точки направлен вдоль касательной к траектории.

Введем направляющий вектор касательной единичной длины:
.
Покажем, что длина этого вектора равна единице. Действительно, поскольку
, то:
.

Здесь мы направили вектор по направлению к вектору скорости, поскольку это более удобно. Но могут возникнуть случаи, когда точка останавливается и движется по той же траектории в обратном направлении. Чтобы не вводить для одной и той же точки траектории два единичных касательных вектора, нужно охватить случай, когда направлен противоположно скорости. Для этого вводят алгебраическую величину скорости:
.
Если направления векторов и совпадают, то . Если они противоположны, то .
– это проекция скорости на направление единичного вектора . Она равна скалярному произведению этих векторов:
.

Абсолютную величину (модуль) вектора скорости мы обозначаем символом с прямыми скобками, или символом без стрелки:
;
Алгебраическая величина скорости:
.

Тогда вектор скорости точки можно представить в следующем виде:
.

Ускорение материальной точки

Аналогично предыдущему, получаем компоненты ускорения (проекции ускорения на оси координат):
;
;
;
.
Модуль ускорения:
.

Тангенциальное (касательное) и нормальное ускорения

Теперь рассмотрим вопрос о направлении вектора ускорения по отношению к траектории. Для этого применим формулу:
.
Дифференцируем ее по времени, применяя правило дифференцирования произведения:
.

Вектор направлен по касательной к траектории. В какую сторону направлена его производная по времени ?

Чтобы ответить на этот вопрос, воспользуемся тем, что длина вектора постоянна и равна единице. Тогда квадрат его длины тоже равен единице:
.
Здесь и далее, два вектора в круглых скобках обозначают их скалярное произведение. Продифференцируем последнее уравнение по времени:
;
;
.
Поскольку скалярное произведение векторов и равно нулю, то эти векторы перпендикулярны друг другу. Так как вектор направлен по касательной к траектории, то вектор перпендикулярен к касательной.

Скорость, касательное и нормальное ускорение точки M

Первую компоненту называют тангенциальным или касательным ускорением:
.
Вторую компоненту называют нормальным ускорением:
.
Тогда полное ускорение:
(2) .
Эта формула представляет собой разложение ускорения на две взаимно перпендикулярные компоненты – касательную к траектории и перпендикулярную к ней.

Тангенциальное (касательное) ускорение

Также как и для скорости, введем алгебраическую величину вектора касательного ускорения :
.
Если , то вектор касательного ускорения сонаправлен с . Если , то эти векторы противоположны. Абсолютную величину касательного ускорения будем обозначать прямыми скобками: . Тогда
.

Умножим обе части уравнения (2) скалярно на :
.
Поскольку , то . Тогда
;
.
Здесь мы положили: .
Отсюда видно, что алгебраическая величина тангенциального ускорения равна проекции полного ускорения на направление касательной к траектории. Она также равна производной по времени алгебраической величины скорости точки: .

Подставив , имеем:
.
Здесь мы учли, что .

Найдем производную по времени модуля скорости . Применяем правила дифференцирования:

;
.

Итак,
.
Отсюда следует, что если между векторами ускорения и скорости острый угол: , то движение ускоренное. Абсолютное значение скорости возрастает. Если между ними тупой угол: , то движение замедленное. Абсолютное значение скорости убывает.

Выразим ускорение через тангенциальное и нормальное: , и учтем, что . Получим:
.
Тогда предыдущую формулировку можно выразить посредством тангенциального ускорения. Если векторы касательного ускорения и скорости направлены в одну сторону, то движение ускоренное. Если их направления противоположны, то движение замедленное.

Радиус кривизны траектории

Теперь исследуем вектор .

Рассмотрим вектор в два момента времени – в момент времени t и в момент t ₁ . Введем обозначения: . По определению производной:
.
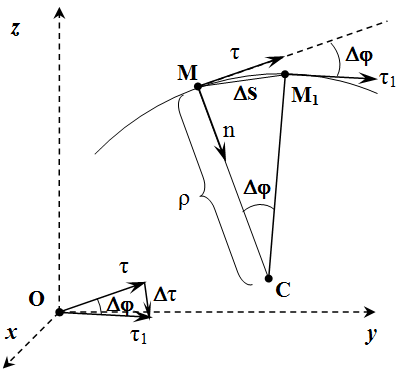
Пусть в момент времени t , точка находится в положении M , а в момент t ₁ – в положении M ₁ (см. рисунок).

Рассмотрим случай, когда алгебраическая скорость положительна: . То есть направления векторов и совпадают. Тогда точка M ₁ находится справа от M . Через точки и проведем плоскости, перпендикулярные векторам и . Пересечение этих плоскостей образует прямую. Она проходит через точку C перпендикулярно плоскости рисунка. MC – это перпендикуляр, опущенный из точки M на эту прямую.

При , точка стремится к точке , а длина отрезка CM стремится к радиусу кривизны траектории ρ . Поскольку и , то угол между отрезками и равен углу между векторами и . Отложим их для наглядности из одного центра.

Абсолютное значение производной:
.
Здесь мы учли, что .

Вектор , как указывалось выше, перпендикулярен . В данном случае он направлен вдоль единичного вектора главной нормали , направленной к центру кривизны C траектории. Поэтому при имеем:
.

Теперь рассмотрим случай, когда алгебраическое значение скорости отрицательно: . В этом случае, вектор скорости противоположен . Получается тот же рисунок, только точка располагается слева от M . В результате абсолютное значение производной остается прежней:
.
Но ее направление меняется на противоположное:
.
Поскольку , то формула сохраняет прежний вид и в этом случае:
.

Нормальное ускорение

Теперь находим нормальное ускорение:
.
Перепишем результат в следующем виде:
,
где ; – единичный вектор в направлении главной нормали траектории – то есть вектор, направленный к мгновенному центру кривизны перпендикулярно касательной к траектории. Поскольку , то также является модулем нормального ускорения. Для него не нужно вводить алгебраическое значение, как мы это делали для скорости и касательного ускорения.
Нормальное ускорение всегда направлено к центру кривизны траектории.

Из формулы (2) имеем:
(4) .
Из формулы (3) находим модуль нормального ускорения:
.

Умножим обе части уравнения (2) скалярно на :
(2) .
.
Поскольку , то . Тогда
;
.
Отсюда видно, что модуль нормального ускорения равен проекции полного ускорения на направление главной нормали.

Выпишем еще раз следующую формулу:
.
Отсюда видно, что нормальное ускорение вызывает изменение направления скорости точки, и оно связано с радиусом кривизны траектории.

Радиус кривизны траектории:
.

И в заключении заметим, что формулу (4) можно переписать в следующем виде:
.
Здесь мы применили формулу для векторного произведения трех векторов:
,
в которую подставили
.

Итак, мы получили:
;
.
Приравняем модули левой и правой частей:
.
Но векторы и взаимно перпендикулярны. Поэтому
.
Тогда
.
Это известная формула из дифференциальной геометрии для кривизны кривой.

Автор: Олег Одинцов . Опубликовано: 09-02-2016 Изменено: 27-01-2020