Векторное уравнение равномерного прямолинейного движения точки
§ 12. Уравнения равномерного прямолинейного движения
1. Уравнение в векторной форме.
Знаем, что одна из основных задач механики заключается в нахождении положения точки в любой момент времени при движении. Знаем, что положение точки может быть определено радиус-вектором, и в любом движении конечный радиус-вектор имеет вид:

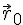
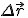
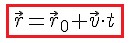
2. Уравнение в координатной форме.
Знаем, что векторы находят с помощью проекций на оси координат. Поэтому от векторного уравнения движения перейдём к проекциям векторных величин на оси координат.
Если 
.
Проекции радиусов равны соответствующим координатам. Поэтому:
.
Если траектория известна, то мы совмещаем траекторию с осью координат OX и пользуемся вместо трёх всего одним первым уравнением.
Никакую часть этого материала ни в каких целях, включая образовательные и научные, нельзя без письменного разрешения владельца авторских прав дублировать в сети Интернет и воспроизводить в какой бы то ни было форме и какими бы то ни было средствами, будь то электронные или механические, включая запись на магнитный или электронный носитель, вывод на печать, фотокопирование.
Векторное уравнение равномерного прямолинейного движения точки
«Физика — 10 класс»
Какая физическая величина характеризует быстроту движений тела?
Как, зная эту величину, определить положение тела?
Движение точки называется равномерным, если она за любые равные промежутки времени проходит одинаковые пути.
Равномерное движение может быть как криволинейным, так и прямолинейным. Равномерное прямолинейное движение — самый простой вид движения. С него мы и начнём изучение движения в кинематике.
Скорость.
Важной величиной, характеризующей движение точки, является её скорость. Некоторое представление о скорости каждый из нас имел и до начала изучения физики.
Черепаха перемещается с малой скоростью, человек движется с большей скоростью, автомобиль движется быстрее человека, а самолёт — ещё быстрее. Самой большой скорости относительно Земли человек достигает с помощью космических ракет.
В механике рассматривают скорость как векторную величину. А это означает, что скорость можно считать известной (заданной) лишь в том случае, если известны её модуль и направление.
Дадим определение скорости равномерного прямолинейного движения точки. Пусть точка, двигаясь равномерно и прямолинейно в течение промежутка времени Δt, переходит из положения М1 в положение М2 (рис. 1.9), совершив при этом перемещение Δ

(При делении вектора на число получаем вектор.) Этот вектор называют скоростью равномерного прямолинейного движения точки и обозначают буквой 
Так как промежуток времени Δt — величина положительная, то скорость направлена так же, как и перемещение Δ
Скоростью равномерного прямолинейного движения точки называется векторная величина, равная отношению перемещения точки к промежутку времени, в течение которого это перемещение произошло.
Модуль перемещения |Δ
Уравнение равномерного прямолинейного движения точки.
Пусть радиус-вектор 




Если начальный момент времени t0 принять равным нулю, то



Последнее уравнение и есть уравнение равномерного прямолинейного движения точки, записанное в векторной форме. Оно позволяет найти радиус-вектор точки при этом движении в любой момент времени, если известны скорость точки и радиус-вектор, задающий её положение в начальный момент времени.
Вместо векторного уравнения (1.4) можно записать три эквивалентных ему уравнения в проекциях на оси координат.
Радиус-вектор 





Уравнение (1.5) есть уравнение равномерного прямолинейного движения точки, записанное в координатной форме.
Оно позволяет найти координату х точки при этом движении в любой момент времени, если известны проекция её скорости на ось ОХ и её начальная координата х0.
Если 

x = x0 + 
y = y0
z = z0,
где х0, у0, z0 — проекции радиус-вектора 
Путь s, пройденный точкой при движении вдоль оси ОХ (рис. 1.10, б), равен модулю изменения её координаты: s = |х2 — х1|. Его можно найти, зная модуль скорости υ = |υx|:
Движение точки может происходить как по направлению оси ОХ (υx = υ), так и в противоположную сторону (υx = -υ). Поэтому при расчётах разумно пользоваться уравнением: х = х0 ± υt.
Отметим, что, строго говоря, равномерного прямолинейного движения не существует. Автомобиль на шоссе никогда не едет абсолютно прямо, небольшие отклонения в ту или иную сторону от прямой всегда имеются. И значение скорости слегка изменяется. Но приближённо на протяжении не слишком большого промежутка времени движение автомобиля можно считать равномерным и прямолинейным с достаточной для практических целей точностью. Таково одно из упрощений действительности, позволяющее без больших усилий описывать многие движения.
Графическое представление равномерного прямолинейного движения.
Полученные результаты можно изобразить наглядно с помощью графиков. Особенно прост график зависимости проекции скорости от времени (рис. 1.11). Это прямая, параллельная оси времени. Площадь прямоугольника ОАВС, заштрихованная на рисунке, равна изменению координаты точки за время t. Ведь сторона ОА есть υx, а сторона ОС — время движения t, поэтому Δx = υxt.
На рисунке 1.12 приведены примеры графиков зависимости координаты от времени для трёх различных случаев равномерного прямолинейного движения. Прямая 1 соответствует случаю х0 = 0, υx1 > 0; прямая 2 — случаю х0 0, а прямая 3 — случаю х0 > 0, υx3
Источник: «Физика — 10 класс», 2014, учебник Мякишев, Буховцев, Сотский
Кинематика — Физика, учебник для 10 класса — Класс!ная физика
Уравнение движения, графики равномерного прямолинейного движения
п.1. Прямолинейное равномерное движение на координатной прямой
Система отсчета, с помощью которой можно описать прямолинейное движение состоит из:
1) тела отсчета; 2) координатной прямой; 3) часов для отсчета времени.
Пусть телом отсчета будет дом.
В начальный момент времени машина стоит в 20 м справа от дома.
Рассмотрим движение машины со скоростью 10 м/с вправо.
Направим координатную прямую параллельно вектору скорости, вправо.
Составим таблицу перемещений за первые 4 секунды:
| t, c | 0 | 1 | 2 | 3 | 4 |
| x, м | 20 | 30 | 40 | 50 | 60 |
Стартуя с точки x0=20, машина каждую секунду удаляется от дома еще на 10 м.
Пройденный путь за 2 секунды – 10·2=20 м, за 3 секунды – 10·3=30 м, за t секунд s=vt метров. Значит, для произвольного времени t можем записать координату x в виде: \begin
Если при тех же начальных условиях и направлении координатной прямой машина будет двигаться влево, получим таблицу:
| t, c | 0 | 1 | 2 | 3 | 4 |
| x, м | 20 | 10 | 0 | -10 | -20 |
В этом случае координата x в любой момент времени t имеет вид: \begin
п.2. Уравнение прямолинейного равномерного движения
Зависимость координаты тела от времени в механике называют уравнением движения.
Если уравнение движения известно, то мы можем решить основную задачу механики.
п.3. Удобная система отсчета для решения задачи о прямолинейном движении
При решении задачи можно выбрать различные тела отсчета и связать с ними различные системы координат. Как правило, некоторая система отсчета является наиболее удобной для решения данной задачи в том смысле, что в ней уравнение движения выглядит и решается проще, чем в других системах.
При решении задач на прямолинейное движение телом отсчета может быть неподвижная поверхность (земля, пол, стол и т.п.), само движущееся тело или другое тело.
При этом системой координат является координатная прямая, параллельная направлению движения (вектору перемещения) тела, уравнение движения которого мы хотим получить.
Проекции скорости и перемещения на координатную прямую могут быть положительными, равными нулю или отрицательными. Величины скорости и перемещения будут равны длинам соответствующих проекций.
п.4. График движения x=x(t)
Сравним полученное уравнение движения \(x(t)=x_0+v_x t\) с уравнением прямой \(y(x)=kx+b\) (см. §38 справочника по алгебре для 7 класса).
В уравнении движения роль углового коэффициента \(k\) играет проекция скорости \(v_x\), а роль свободного члена \(b\) – начальная координата \(x_0\).
 | Построим графики зависимости координаты от времени для нашего примера: |
x=20+10t — машина движется вправо (в направлении оси OX)
x=20-10t — машина движется влево (в направлении, противоположном оси OX)
x=20 — машина стоит
п.5. Как найти уравнение движения по графику движения?
п.6. График скорости vx=vx(t)
Для рассмотренного примера:
п.7. Как найти путь и перемещение по графику скорости?
Пусть тело движется прямолинейно равномерно, зависимость его координаты от времени описывается уравнением: $$ x(t)=x_0+v_x t $$ Тогда в некоторый момент времени \(t_1\) координата равна \(x_1=x_0+v_x t_1\).
Несколько позже, в момент времени \(t_2\gt t_1\) координата равна \(x_2=x_0+v_x t_2\).
Если \(v_x\gt 0\), то пройденный за промежуток времени \(\triangle t=t_2-t_1\) путь равен разности координат: $$ s=x_2-x_1=(x_0+v_x t_2)-(x_0+v_x t_1)=x_0-x_0+v_x (t_2-t_1)=v_x \triangle t $$ В общем случае, т.к. \(v_x\) может быть и отрицательным, а путь всегда положительный, в формуле нужно поставить модуль: $$ s=|v_x|\triangle t $$
Изобразим полученное соотношение на графике скорости:
Проекция скорости \(v_x\) может быть не только положительной, но и отрицательной.
Если учитывать знак, то произведение: $$ \triangle x=v_x \triangle t $$ дает проекцию перемещения на ось OX. Знак этого произведения указывает на направление перемещения.
Проекция перемещения может быть как положительной, так и отрицательной или равной 0.
п.8. Задачи
Задача 1. Спортсмен бежит по прямолинейному участку дистанции с постоянной скоростью 8 м/с. Примите \(x_0=0\) и запишите уравнение движения.
а) Постройте график движения \(x=x(t)\) и найдите с его помощью, сколько пробежит спортсмен за \(t_1=5\ с\), за \(t_2=10\ с\);
б) постройте график скорости \(v=v(t)\) и найдите с его помощью, какой путь преодолеет спортсмен за промежуток времени \(\triangle t=t_2-t_1\)?
По условию \(x_0=0,\ v_x=8\).
Уравнение движения: \(x=x_0+v_x t=0+8t=8t\)
а) Строим график прямой \(x=8t\) по двум точкам:
| t | 0 | 5 |
| x | 0 | 40 |
По графику находим: \begin
б) Скорость \(v_x=8\) м/с — постоянная величина, её график:
$$ t_1=5\ с,\ \ t_2=10\ с $$ Пройденный путь за промежуток времени \(\triangle t=t_2-t_1\) равен площади заштрихованного прямоугольника: $$ s=v_x \triangle t=8\cdot (10-5)=40\ \text <(м)>$$ Ответ: а) 40 м и 80 м; б) 40 м
Задача 2. Космический корабль движется прямолинейно с постоянной скоростью.
Известно, что через 1 час после старта корабль находился на расстоянии 38 тыс.км от астероида Веста, а через 2 часа после старта – на расстоянии 56 тыс.км.
а) постройте график движения корабля, найдите по графику уравнение движения.
б) на каком расстоянии от астероида находился корабль в начальный момент времени?
в) на каком расстоянии от астероида будет находиться корабль через 4 часа после старта?
г) чему равна скорость корабля в километрах в секунду?
а) Будем откладывать время в часах, а расстояние в тыс.км
Отмечаем точки A(1;38) и B(2;56), проводим через них прямую.
Полученная прямая и есть график движения \(x=x(t)\).
Найдем скорость корабля \(v_x\): $$ v_x=\frac
б) В начальный момент времени корабль находился на расстоянии \(x_0=20\) тыс.км от астероида.
в) Через 4 часа после старта корабль будет находиться на расстоянии $$ x(4)=20+18\cdot 4=92\ (\text<тыс.км>) $$
г) Переведем скорость в км/с: $$ 18000\frac<\text<км>><\text<ч>>=\frac<18000\ \text<км>><1\ \text<ч>>=\frac<18000\ \text<км>><3600\ \text
а) \(x(t)=20+18t\) (\(x\) в тыс.км, \(t\) в часах); б) 20 тыс.км; в) 92 тыс.км; г) 5 км/с
http://class-fizika.ru/10_a5.html
http://reshator.com/sprav/fizika/7-klass/uravnenie-dvizheniya-grafiki-ravnomernogo-pryamolinejnogo-dvizheniya/
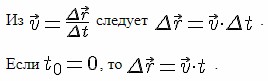
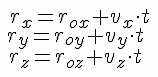 .
.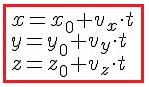 .
.