Векторный метод решения систем линейных уравнений

Решение систем линейных уравнений

Эта страничка поможет решить Системы Линейных Алгебраических Уравнений (СЛАУ) методом Гаусса, матричным методом или методом Крамера, исследовать их на совместность (теорема Кронекера-Капелли), определить количество решений, найти общее, частное и базисные решения.

Введите коэффициенты при неизвестных в поля. Если Ваше уравнение имеет меньшее количество неизвестных, то оставьте пустыми поля при переменных, не входящих в ваше уравнение. Можно использовать дроби ( 13/31 ).

Лекции по высшей математике, линейная алгебра (стр. 4 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4

Запишем в разных видах систему уравнений .

· = — матричный вид;

x 1 + x 2 = — векторный вид;

Вектор`x * = называется решением системы линейных уравнений, если при подстановке его координат в уравнения системы все уравнения обращаются в верные равенства.

Система уравнений называется совместной, если она имеет хотя бы одно решение.

Система уравнений называется несовместной, если она не имеет ни одного решения.

Система уравнений называется определенной, если она имеет ровно одно решение.

Система уравнений называется неопределенной, если она имеет более одного решения.

2. СИСТЕМЫ n ЛИНЕЙНЫХ УРАВНЕНИЙ С n НЕИЗВЕСТНЫМИ.

Квадратная матрица A называется невырожденной, если ее строки линейно независимы.

Согласно этому определению, свойствам определителей, критерию существования обратной матрицы получаем, что невырожденная матрица имеет ненулевой определитель и обладает обратной матрицей.

Благодаря этим свойствам имеем два особых метода решения системы A`x =`b с квадратной невырожденной матрицей A.

МАТРИЧНЫЙ МЕТОД РЕШЕНИЯ СЛУ.

Если матрица A системы A`x =`b квадратная невырожденная, то существует единственное решение`x * этой системы, равное произведению обратной матрицы A– 1 на столбец свободных членов`b, `x * = A– 1`b.

Докажем сначала, что вектор`x * является решением системы A`x =`b. В самом деле, A`x * = A · A– 1`b = E`b =`b, то есть A`x * =`b и`x * является решением системы A`x =`b.

Докажем теперь единственность этого решения. Предположим, что имеется еще другое решение`x 1, то есть A`x 1 =`b — верное равенство. Домножим обе части этого равенства слева на A– 1. Получим A– 1 A`x 1 = A– 1`b и, следовательно,`x 1 = A– 1`b, то есть`x 1 =`x *. Теорема доказана.

Таким образом, матричный метод решения системы A`x =`b с квадратной невырожденной матрицей A состоит в нахождении решения этой системы по формуле`x * = A– 1`b.

Если матрица A системы A`x =`b квадратная невырожденная, то существует единственное решение`x * = этой системы, которое может быть найдено по формулам:

, , … , , где D — определитель матрицы A, D j — определитель, полученный из D заменой в нем j –го столбца на столбец свободных членов`b (для всех j = 1, 2, … , n).

ПРИМЕР решения системы линейных уравнений по правилу Крамера.

.

D = = 1 + 6 = 7, D 1 = = 0 + 14 = 14, D 2 = = 7 – 0 = 7,

= 2, = 1,`x * = .

3. ОБЩИЕ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ.

Рассмотрим систему уравнений A`x =`b с произвольной матрицей A. Исследуем вопрос о ее совместности и количестве решений.

ТЕОРЕМА КРОНЕКЕРА – КАПЕЛЛИ.

Для того, чтобы система уравнений A`x =`b была совместной, необходимо и достаточно, чтобы ранг матрицы этой системы равнялся рангу ее расширенной матрицы.

1) Пусть система уравнений A`x =`b является совместной. Докажем, что ранг r A матрицы A равняется рангу r à расширенной матрицы Ã.

Представим матрицы A и Ã как системы их векторов столбцов

соответственно. Ранг матрицы A равен рангу системы векторов (1), а ранг матрицы Ã равен рангу системы векторов (2). Поскольку система векторов (1) является подсистемой системы векторов (2), то r A £ r Ã.

Так как система A`x =`b является совместной, то существует вектор `x * = , координаты которого удовлетворяют данной системе, или, в векторном виде, имеет место равенство x 1*`A 1 + x 2*`A 2 + … + x n*`A n =`b. Отсюда следует, что`b Î L (`A 1,`A 2 , … ,`A n ) и, следовательно,

`A 1,`A 2 , … ,`A n ,`b Î L (`A 1,`A 2 , … ,`A n ). По свойствам ранга системы векторов r à £ r A. Но так как r A £ r à , то r A = r à .

2) Пусть теперь r A = r à = r. Докажем, что система A`x =`b является совместной. Согласно определению базиса системы векторов базисы систем (1) и (2) содержат по r векторов. Пусть`A 1, `A 2 , … ,`A r — базис системы (1). Тогда эти же векторы будут являться и базисом системы (2). Действительно, векторы`A 1,`A 2 , … ,`A r образуют линейно независимую подсистему системы (2), а поскольку их количество совпадает с рангом системы (2), то они являются базисом этой системы. Следовательно, вектор`b можно представить в виде линейной комбинации векторов`A 1,`A 2 , …,`A r :

`b = l 1`A 1 + l 2`A 2 + … + l r`A r, а также в виде линейной комбинации

`b = l 1`A 1 + l 2`A 2 + … + l r`A r + 0`A r + 1 + … + 0`A n. Справедливость последнего равенства означает, что вектор`x *, координатами которого являются числа l 1, l 2 , … , l r , 0, … , 0 является решением системы уравнений A`x =`b, то есть система A`x =`b совместна. Теорема доказана.

ТЕОРЕМА ОБ ОПРЕДЕЛЕННОСТИ СЛУ.

Пусть система уравнений A`x =`b является совместной, имеет n неизвестных и r A = r à = r.

Метод Гаусса онлайн

Данный онлайн калькулятор находит решение системы линейных уравнений (СЛУ) методом Гаусса. Дается подробное решение. Для вычисления выбирайте количество переменных и количество уравнений. Затем введите данные в ячейки и нажимайте на кнопку «Вычислить.»

Предупреждение

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Метод Гаусса

Метод Гаусса − это метод перехода от исходной системы линейных уравнений (при помощи эквивалентных преобразований) к системе, которая решается проще, чем исходная система.

Эквивалентными преобразованиями системы линейных уравнений являются:

• перемена местами двух уравнений в системе,
• умножение какого-либо уравнения в системе на ненулевое действительное число,
• прибавление к одному уравнению другого уравнения, умноженного на произвольное число.

Рассмотрим систему линейных уравнений:

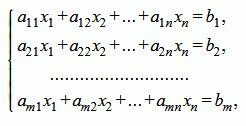(1)

Запишем систему (1) в матричном виде:

(3)

A-называется матрица коэффициентов системы, b − правая часть ограничений, x− вектор переменных, которую нужно найти. Пусть rang(A)=p.

Эквивалентные преобразования не меняют ранг матрицы коэффициентов и ранг расширеннной матрицы системы. Не меняется также множество решений системы при эквивалентных преобразованиях. Суть метода Гаусса заключается в приведении матрцы коэффициентов A к диагональному или ступенчатому.

Построим расшренную матрицу системы:

(4)

Предположим a₁₁≠0. Если это не так, то можно поменять местами эту строку со строкой с ненулевым элементом в столбце 1 (если нет таких строк, то переходим к следующему столбцу). Обнуляем все элементы столбца 1 ниже ведущего элемента a₁₁. Для этого сложим строки 2,3, . m со строкой 1, умноженной на −a₂₁/a₁₁, −a₃₁/a₁₁, . −a_m1/a₁₁, соответственно. Тогда (4) примет следующий вид:

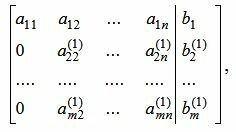(5)

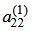
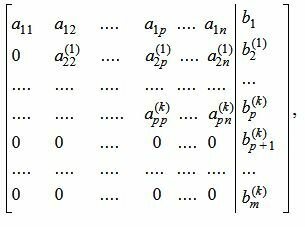На следующем этапе обнуляем все элементы столбца 2, ниже элемента . Если данный элемент нулевой, то эту строку меняем местами со строкой, лежащий ниже данной строки и имеющий ненулевой элемент во втором столбце. Далее обнуляем все элементы столбца 2 ниже ведущего элемента a₂₂. Для этого сложим строки 3, . m со строкой 2, умноженной на −a₃₂/a₂₂, . −a_m2/a₂₂, соответственно. Продолжая процедуру, получим матрицу диагонального или ступенчатого вида. Пусть полученная расширенная матрица имеет вид:

(6)

Обратим внимание на последние строки. Если 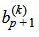. равны нулю, то система линейных уравнений имеет решение, если же хотя бы один из этих чисел отлично от нуля, то система несовместна. Иными словами, система (2) совместна тогда и только тогда, когда ранг матрицы A навен рангу расширенной матрицы (A|b).

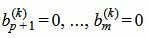
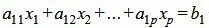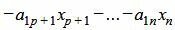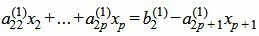Пусть . Тогда

(7)

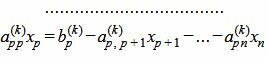Так как rangA=rang(A|b), то множество решений (7) есть (n−p)− многообразие. Следовательно n−p неизвестных можно выбрать произвольно. Остальные неизвестные из системы (7) вычисляются так. Из последнего уравнения выражаем x_p через остальные переменные и вставляем в предыдущие выражения. Далее из предпоследнего уравнения выражаем x_p−1 через остальные переменные и вставляем в предыдущие выражения и т.д. Рассмотрим метод Гаусса на конкретных примерах.

Примеры решения системы линейных уравнений методом Гаусса

Пример 1. Найти общее решение системы линейных уравнений методом Гаусса:

Матричный вид записи: Ax=b, где

Для решения системы, запишем расширенную матрицу:

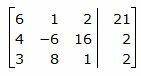Обозначим через a_ij элементы i-ой строки и j-ого столбца.

Исключим элементы 1-го столбца матрицы ниже элемента a_{1 1}. Для этого сложим строки 2,3 со строкой 1, умноженной на -2/3,-1/2 соответственно:

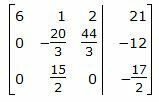Исключим элементы 2-го столбца матрицы ниже элемента a2 2. Для этого сложим строку 3 со строкой 2, умноженной на 9/8:

Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):

Из вышеизложенной таблицы можно записать:

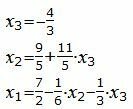Подставив верхние выражения в нижние, получим решение.

,,.

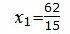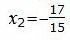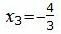Пример 2. Найти общее решение системы линейных уравнений методом Гаусса:

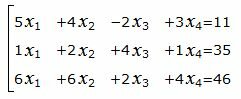Матричный вид записи: Ax=b, где

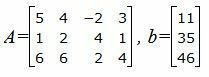Для решения системы, построим расширенную матрицу:

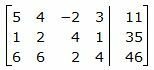Обозначим через a_ij элементы i-ой строки и j-ого столбца.

Исключим элементы 1-го столбца матрицы ниже элемента a₁₁. Для этого сложим строки 2,3 со строкой 1, умноженной на -1/5,-6/5 соответственно:

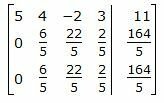Исключим элементы 2-го столбца матрицы ниже элемента a₂₂. Для этого сложим строку 3 со строкой 2, умноженной на -1:

Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):

Выразим переменные x₁, x₂ относительно остальных переменных.

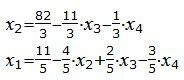где x₃, x₄− произвольные действительные числа.

Подставив верхние выражения в нижние, получим решение.

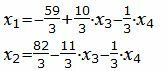где x₃, x₄− произвольные действительные числа.

Векторный вариант решения:

Запишем вышеизложенное решение, представив свободные переменные в виде тождеств:

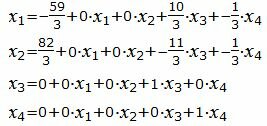Тогда векторное решение можно представить так:

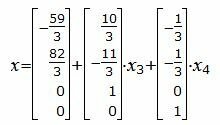где x₃, x₄− произвольные действительные числа.