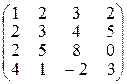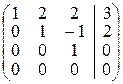Векторное пространство: размерность и базис, разложение вектора по базису
В статье о n -мерных векторах мы пришли к понятию линейного пространства, порождаемого множеством n -мерных векторов. Теперь нам предстоит рассмотреть не менее важные понятия, такие как размерность и базис векторного пространства. Они напрямую связаны с понятием линейно независимой системы векторов, так что дополнительно рекомендуется напомнить себе основы и этой темы.
Введем некоторые определения.
Размерность векторного пространства – число, соответствующее максимальному количеству линейно независимых векторов в этом пространстве.
Базис векторного пространства – совокупность линейно независимых векторов, упорядоченная и в своей численности равная размерности пространства.
Рассмотрим некое пространство n -векторов. Размерность его соответственно равна n . Возьмем систему из n -единичных векторов:
e ( 1 ) = ( 1 , 0 , . . . , 0 ) e ( 2 ) = ( 0 , 1 , . . . , 0 ) e ( n ) = ( 0 , 0 , . . . , 1 )
Используем эти векторы в качестве составляющих матрицы A : она будет являться единичной с размерностью n на n . Ранг этой матрицы равен n . Следовательно, векторная система e ( 1 ) , e ( 2 ) , . . . , e ( n ) является линейно независимой. При этом к системе невозможно добавить ни одного вектора, не нарушив ее линейной независимости.
Так как число векторов в системе равно n , то размерность пространства n -мерных векторов равна n , а единичные векторы e ( 1 ) , e ( 2 ) , . . . , e ( n ) являются базисом указанного пространства.
Из полученного определения сделаем вывод: любая система n -мерных векторов, в которой число векторов меньше n , не является базисом пространства.
Если мы поменяем местами первый и второй вектор, получим систему векторов e ( 2 ) , e ( 1 ) , . . . , e ( n ) . Она также будет являться базисом n -мерного векторного пространства. Составим матрицу, взяв за ее строки векторы полученной системы. Матрица может быть получена из единичной матрицы перестановкой местами первых двух строк, ранг ее будет равен n . Система e ( 2 ) , e ( 1 ) , . . . , e ( n ) линейно независима и является базисом n -мерного векторного пространства.
Переставив местами в исходной системе другие векторы, получим еще один базис.
Мы можем взять линейно независимую систему неединичных векторов, и она также будет представлять собой базис n -мерного векторного пространства.
Векторное пространство с размерностью n имеет столько базисов, сколько существует линейно независимых систем из n -мерных векторов числом n.
Плоскость является двумерным пространством – ее базисом будут два любых неколлинеарных вектора. Базисом трехмерного пространства послужат три любых некомпланарных вектора.
Рассмотрим применение данной теории на конкретных примерах.
Исходные данные: векторы
a = ( 3 , — 2 , 1 ) b = ( 2 , 1 , 2 ) c = ( 3 , — 1 , — 2 )
Необходимо определить, являются ли указанные векторы базисом трехмерного векторного пространства.
Решение
Для решения поставленной задачи исследуем заданную систему векторов на линейную зависимость. Составим матрицу, где строки – координаты векторов. Определим ранг матрицы.
A = 3 2 3 — 2 1 — 1 1 2 — 2 A = 3 — 2 1 2 1 2 3 — 1 — 2 = 3 · 1 · ( — 2 ) + ( — 2 ) · 2 · 3 + 1 · 2 · ( — 1 ) — 1 · 1 · 3 — ( — 2 ) · 2 · ( — 2 ) — 3 · 2 · ( — 1 ) = = — 25 ≠ 0 ⇒ R a n k ( A ) = 3
Следовательно, заданные условием задачи векторы линейно независимы, и их численность равна размерности векторного пространства – они являются базисом векторного пространства.
Ответ: указанные векторы являются базисом векторного пространства.
Исходные данные: векторы
a = ( 3 , — 2 , 1 ) b = ( 2 , 1 , 2 ) c = ( 3 , — 1 , — 2 ) d = ( 0 , 1 , 2 )
Необходимо определить, может ли указанная система векторов являться базисом трехмерного пространства.
Решение
Указанная в условии задачи система векторов является линейно зависимой, т.к. максимальное число линейно независимых векторов равно 3. Таким образом, указанная система векторов не может служить базисом трехмерного векторного пространства. Но стоит отметить, что подсистема исходной системы a = ( 3 , — 2 , 1 ) , b = ( 2 , 1 , 2 ) , c = ( 3 , — 1 , — 2 ) является базисом.
Ответ: указанная система векторов не является базисом.
Исходные данные: векторы
a = ( 1 , 2 , 3 , 3 ) b = ( 2 , 5 , 6 , 8 ) c = ( 1 , 3 , 2 , 4 ) d = ( 2 , 5 , 4 , 7 )
Могут ли они являться базисом четырехмерного пространства?
Решение
Cоставим матрицу, используя в качестве строк координаты заданных векторов
A = 1 2 3 3 2 5 6 8 1 3 2 4 2 5 4 7
По методу Гаусса определим ранг матрицы:
A = 1 2 3 3 2 5 6 8 1 3 2 4 2 5 4 7
1 2 3 3 0 1 0 2 0 1 — 1 1 0 1 — 2 1
1 2 3 3 0 1 0 2 0 0 — 1 — 1 0 0 — 2 — 1
1 2 3 3 0 1 0 2 0 0 — 1 — 1 0 0 0 1 ⇒ ⇒ R a n k ( A ) = 4
Следовательно, система заданных векторов линейно независима и их численность равна размерности векторного пространства – они являются базисом четырехмерного векторного пространства.
Ответ: заданные векторы являются базисом четырехмерного пространства.
Исходные данные: векторы
a ( 1 ) = ( 1 , 2 , — 1 , — 2 ) a ( 2 ) = ( 0 , 2 , 1 , — 3 ) a ( 3 ) = ( 1 , 0 , 0 , 5 )
Составляют ли они базис пространства размерностью 4?
Решение
Исходная система векторов линейно независима, но численность векторов в ней недостаточна, чтобы стать базисом четырехмерного пространства.
Ответ: нет, не составляют.
Разложение вектора по базису
Примем, что произвольные векторы e ( 1 ) , e ( 2 ) , . . . , e ( n ) являются базисом векторного n-мерного пространства. Добавим к ним некий n -мерный вектор x → : полученная система векторов станет линейно зависимой. Свойства линейной зависимости гласят, что хотя бы один из векторов такой системы может линейно выражаться через остальные. Переформулируя это утверждение, можно говорить о том, что хотя бы один из векторов линейно зависимой системы может раскладываться по остальным векторам.
Таким образом, мы пришли к формулировке важнейшей теоремы:
Любой вектор n -мерного векторного пространства единственным образом раскладывается по базису.
Докажем эту теорему:
зададим базис n -мерного векторного пространства — e ( 1 ) , e ( 2 ) , . . . , e ( n ) . Сделаем систему линейно зависимой, добавив к ней n -мерный вектор x → . Этот вектор может быть линейно выражен через исходные векторы e :
x = x 1 · e ( 1 ) + x 2 · e ( 2 ) + . . . + x n · e ( n ) , где x 1 , x 2 , . . . , x n — некоторые числа.
Теперь докажем, что такое разложение является единственным. Предположим, что это не так и существует еще одно подобное разложение:
Отнимем от левой и правой частей этого равенства соответственно левую и правую части равенства x = x 1 · e ( 1 ) + x 2 · e ( 2 ) + . . . + x n · e ( n ) . Получим:
1 — x 1 ) · e ( 1 ) + ( x
2 — x 2 ) · e ( 2 ) + . . . ( x
Система базисных векторов e ( 1 ) , e ( 2 ) , . . . , e ( n ) линейно независима; по определению линейной независимости системы векторов равенство выше возможно только тогда, когда все коэффициенты ( x
2 — x 2 ) , . . . , ( x
n — x n ) будут равны нулю. Из чего справедливым будет: x 1 = x
n . И это доказывает единственный вариант разложения вектора по базису.
При этом коэффициенты x 1 , x 2 , . . . , x n называются координатами вектора x → в базисе e ( 1 ) , e ( 2 ) , . . . , e ( n ) .
Доказанная теория делает понятным выражение «задан n -мерный вектор x = ( x 1 , x 2 , . . . , x n ) »: рассматривается вектор x → n -мерного векторного пространства, и его координаты заданы в некотором базисе. При этом также понятно, что этот же вектор в другом базисе n -мерного пространства будет иметь другие координаты.
Рассмотрим следующий пример: допустим, что в некотором базисе n -мерного векторного пространства задана система из n линейно независимых векторов
e ( 1 ) = ( e 1 ( 1 ) , e 2 ( 1 ) , . . . , e n ( 1 ) ) e ( 2 ) = ( e 1 ( 2 ) , e 2 ( 2 ) , . . . , e n ( 2 ) ) ⋮ e ( n ) = ( e 1 ( n ) , e 2 ( n ) , . . . , e n ( n ) )
а также задан вектор x = ( x 1 , x 2 , . . . , x n ) .
Векторы e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) в этом случае также являются базисом этого векторного пространства.
Предположим, что необходимо определить координаты вектора x → в базисе e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) , обозначаемые как x
Вектор x → будет представлен следующим образом:
2 · e ( 2 ) + . . . + x
Запишем это выражение в координатной форме:
( x 1 , x 2 , . . . , x n ) = x
1 · ( e ( 1 ) 1 , e ( 1 ) 2 , . . . , e ( 1 ) n ) + x
2 · ( e ( 2 ) 1 , e ( 2 ) 2 , . . . , e ( 2 ) n ) + . . . + + x
n · ( e ( n ) 1 , e ( n ) 2 , . . . , e ( n ) n ) = = ( x
2 e 1 ( 2 ) + . . . + x
2 e 2 ( 2 ) + + . . . + x
n e 2 ( n ) , . . . , x
2 e n ( 2 ) + . . . + x
Полученное равенство равносильно системе из n линейных алгебраических выражений с n неизвестными линейными переменными x
n e 2 n ⋮ x n = x
Матрица этой системы будет иметь следующий вид:
e 1 ( 1 ) e 1 ( 2 ) ⋯ e 1 ( n ) e 2 ( 1 ) e 2 ( 2 ) ⋯ e 2 ( n ) ⋮ ⋮ ⋮ ⋮ e n ( 1 ) e n ( 2 ) ⋯ e n ( n )
Пусть это будет матрица A , и ее столбцы – векторы линейно независимой системы векторов e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) . Ранг матрицы – n , и ее определитель отличен от нуля. Это свидетельствует о том, что система уравнений имеет единственное решение, определяемое любым удобным способом: к примеру, методом Крамера или матричным методом. Таким образом мы сможем определить координаты x
n вектора x → в базисе e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) .
Применим рассмотренную теорию на конкретном примере.
Исходные данные: в базисе трехмерного пространства заданы векторы
e ( 1 ) = ( 1 , — 1 , 1 ) e ( 2 ) = ( 3 , 2 , — 5 ) e ( 3 ) = ( 2 , 1 , — 3 ) x = ( 6 , 2 , — 7 )
Необходимо подтвердить факт, что система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) также служит базисом заданного пространства, а также определить координаты вектора х в заданном базисе.
Решение
Система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) будет являться базисом трехмерного пространства, если она линейно независима. Выясним эту возможность, определив ранг матрицы A , строки которой – заданные векторы e ( 1 ) , e ( 2 ) , e ( 3 ) .
Используем метод Гаусса:
A = 1 — 1 1 3 2 — 5 2 1 — 3
1 — 1 1 0 5 — 8 0 3 — 5
1 — 1 1 0 5 — 8 0 0 — 1 5
R a n k ( A ) = 3 . Таким образом, система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) линейно независима и является базисом.
Пусть в базисе вектор x → имеет координаты x
3 . Связь этих координат определяется уравнением:
3 e 1 ( 3 ) x 2 = x
3 e 2 ( 3 ) x 3 = x
Применим значения согласно условиям задачи:
Решим систему уравнений методом Крамера:
∆ = 1 3 2 — 1 2 1 1 — 5 — 3 = — 1 ∆ x
1 = 6 3 2 2 2 1 — 7 — 5 — 3 = — 1 , x
1 ∆ = — 1 — 1 = 1 ∆ x
2 = 1 6 2 — 1 2 1 1 — 7 — 3 = — 1 , x
2 ∆ = — 1 — 1 = 1 ∆ x
3 = 1 3 6 — 1 2 2 1 — 5 — 7 = — 1 , x
Так, вектор x → в базисе e ( 1 ) , e ( 2 ) , e ( 3 ) имеет координаты x
Ответ: x = ( 1 , 1 , 1 )
Связь между базисами
Предположим, что в некотором базисе n-мерного векторного пространства даны две линейно независимые системы векторов:
c ( 1 ) = ( c 1 ( 1 ) , c 2 ( 1 ) , . . . , c n ( 1 ) ) c ( 2 ) = ( c 1 ( 2 ) , c 2 ( 2 ) , . . . , c n ( 2 ) ) ⋮ c ( n ) = ( c 1 ( n ) , e 2 ( n ) , . . . , c n ( n ) )
e ( 1 ) = ( e 1 ( 1 ) , e 2 ( 1 ) , . . . , e n ( 1 ) ) e ( 2 ) = ( e 1 ( 2 ) , e 2 ( 2 ) , . . . , e n ( 2 ) ) ⋮ e ( n ) = ( e 1 ( n ) , e 2 ( n ) , . . . , e n ( n ) )
Указанные системы являются также базисами заданного пространства.
n ( 1 ) — координаты вектора c ( 1 ) в базисе e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) , тогда связь координат будет задаваться системой линейных уравнений:
1 ( 1 ) e 1 ( 1 ) + c
2 ( 1 ) e 1 ( 2 ) + . . . + c
n ( 1 ) e 1 ( n ) с 2 ( 1 ) = c
1 ( 1 ) e 2 ( 1 ) + c
2 ( 1 ) e 2 ( 2 ) + . . . + c
n ( 1 ) e 2 ( n ) ⋮ с n ( 1 ) = c
1 ( 1 ) e n ( 1 ) + c
2 ( 1 ) e n ( 2 ) + . . . + c
В виде матрицы систему можно отобразить так:
( c 1 ( 1 ) , c 2 ( 1 ) , . . . , c n ( 1 ) ) = ( c
n ( 1 ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )
Сделаем по аналогии такую же запись для вектора c ( 2 ) :
( c 1 ( 2 ) , c 2 ( 2 ) , . . . , c n ( 2 ) ) = ( c
n ( 2 ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )
И, далее действуя по тому же принципу, получаем:
( c 1 ( n ) , c 2 ( n ) , . . . , c n ( n ) ) = ( c
n ( n ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )
Матричные равенства объединим в одно выражение:
c 1 ( 1 ) c 2 ( 1 ) ⋯ c n ( 1 ) c 1 ( 2 ) c 2 ( 2 ) ⋯ c n ( 2 ) ⋮ ⋮ ⋮ ⋮ c 1 ( n ) c 2 ( n ) ⋯ c n ( n ) = c
n ( n ) · e 1 ( 1 ) e 2 ( 1 ) ⋯ e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) ⋯ e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) ⋯ e n ( n )
Оно и будет определять связь векторов двух различных базисов.
Используя тот же принцип, возможно выразить все векторы базиса e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) через базис c ( 1 ) , c ( 2 ) , . . . , c ( n ) :
e 1 ( 1 ) e 2 ( 1 ) ⋯ e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) ⋯ e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) ⋯ e n ( n ) = e
n ( n ) · c 1 ( 1 ) c 2 ( 1 ) ⋯ c n ( 1 ) c 1 ( 2 ) c 2 ( 2 ) ⋯ c n ( 2 ) ⋮ ⋮ ⋮ ⋮ c 1 ( n ) c 2 ( n ) ⋯ c n ( n )
Дадим следующие определения:
n ( n ) является матрицей перехода от базиса e ( 1 ) , e ( 2 ) , . . . , e ( 3 )
к базису c ( 1 ) , c ( 2 ) , . . . , c ( n ) .
n ( n ) является матрицей перехода от базиса c ( 1 ) , c ( 2 ) , . . . , c ( n )
к базису e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) .
Линейная зависимость. Базис системы векторов
В геометрии вектор понимается как направленный отрезок, причем векторы, полученные один из другого параллельным переносом, считаются равными. Все равные векторы рассматриваются как один и тот же вектор. Начало вектора можно поместить в любую точку пространства или плоскости.
Если в пространстве заданы координаты концов вектора 

Аналогичная формула имеет место на плоскости. Это значит, что вектор можно записать в виде координатной строки. Операции над векторами, – сложение и умножение на число, над строками выполняются покомпонентно. Это дает возможность расширить понятие вектора, понимая под вектором любую строку чисел. Например, решение системы линейных уравнений, а также любой набор значений переменных системы, можно рассматривать как вектор.
Над строками одинаковой длины операция сложения выполняется по правилу
Умножение строки на число выполняется по правилу
Множество векторов-строк заданной длины n с указанными операциями сложения векторов и умножения на число образует алгебраическую структуру, которая называется n-мерным линейным пространством.
Линейной комбинацией векторов 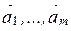
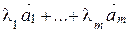
Система векторов 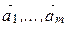
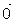
Система векторов 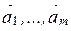
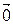
Таким образом, решение вопроса о линейной зависимости системы векторов 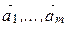
x1 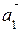
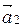

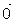
Если у этого уравнения есть ненулевые решения, то система векторов линейно зависима. Если же нулевое решение является единственным, то система векторов линейно независима.
Для решения системы (4) можно для наглядности векторы записать не в виде строк, а в виде столбцов.
Тогда, выполнив преобразования в левой части, придем к системе линейных уравнений, равносильной уравнению (4). Основная матрица этой системы образована координатами исходных векторов, расположенных по столбцам. Столбец свободных членов здесь не нужен, так как система однородная.
Базисом системы векторов (конечной или бесконечной, в частности, всего линейного пространства) называется ее непустая линейно независимая подсистема, через которую можно выразить любой вектор системы.
Пример 1.5.2.Найти базис системы векторов 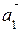
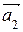

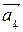
Решение. Строим матрицу, в которой координаты данных векторов располагаем по столбцам. Это матрица системы x1 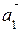
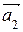

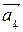
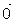
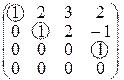
Базис данной системы векторов образуют векторы 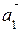
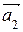
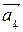

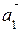
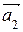
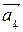




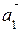
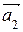
Замечание. Если требуется выразить через базис несколько векторов, то для каждого из них строится соответствующая система линейных уравнений. Эти системы будут отличаться только столбцами свободных членов. При этом каждая система решается независимо от остальных.
У п р а ж н е н и е 1.4. Найти базис системы векторов и выразить остальные векторы через базис:
а) 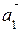
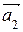

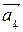
б) 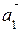
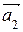

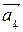
в) 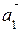
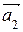

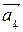
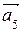
В заданной системе векторов базис обычно можно выделить разными способами, но во всех базисах будет одинаковое число векторов. Число векторов в базисе линейного пространства называется размерностью пространства. Для n-мерного линейного пространства n – это размерность пространства, так как это пространство имеет стандартный базис 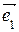
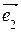



= a1(1, 0, … , 0) + a2(0, 1, … , 0) + … + an(0, 0, … ,1) = a1 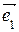
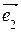

Таким образом, компоненты в строке вектора 
Прямые на плоскости
Задача аналитической геометрии – применение к геометрическим задачам координатного метода. Тем самым задача переводится в алгебраическую форму и решается средствами алгебры.
В прямоугольной декартовой системе координат каждой точке соответствует пара чисел – ее координаты.
Рассмотрим произвольное уравнение от двух переменных F(x, y) = 0. Изобразив на плоскости точки координаты которых (x, y) удовлетворяют уравнению, получим некоторую фигуру. Исходное уравнение является уравнением этой фигуры. Вместо уравнения может фигурировать неравенство или другое условие – каждое такое условие всегда можно записать в виде уравнения.
Пересечение двух фигур задается системой уравнений, определяющих эти фигуры.
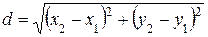
Пример 1.4.1.Построить уравнение окружности с центром в точке А(a, b) и радиусом r.
Обозначим произвольную точку окружности через M(x, y), тогда, согласно определению, окружность задается уравнением АМ = r. Воспользовавшись формулой (1), получаем алгебраическое уравнение 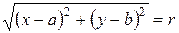
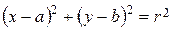
Решение задач методом Гаусса
Содержание:
Решение задач методом Гаусса. Применение метода Гаусса к задачам линейной зависимости систем векторов
Мы уже говорили о том, что одной из важных задач линейной алгебры является выяснение факта — линейно зависима или независима в пространстве 

Определение 1. Линейное уравнение называется однородным, если свободный член уравнения равен нулю. Система, состоящая из однородных уравнений, сама называется однородной.
Однородная система 


Однородная система всегда совместна, т.к. одним из ее решений является 
Это решение называют нулевым. Важно знать имеет ли конкретная однородная система ненулевые решения.
Теорема 1. Однородная линейная система, в которой число уравнений меньше числа неизвестных, всегда имеет ненулевое решение.
Заметим, что система (1) может быть записана в векторном виде

В этой записи участвуют 
Т.о., неизвестные 



Пример №19
Дана система из четырех векторов, принадлежащих 

Является ли эта система линейно зависимой в 
Решение:
Запишем уравнение 
Если система уравнений (4) имеет только нулевое решение, то система векторов (3) линейно независима в 
Применим к системе уравнений (4) метод Гаусса:
Получилась система уравнений с базисными неизвестными 


Индекс цен и индекс инфляции. Ортогональные векторы
Одним из способов определения индекса цен и уровня инфляции является расчет стоимости «потребительской корзины», состоящей из основных видов товаров и услуг, получаемых потребителями. Обычно это 300 необходимых видов товаров и услуг. В табл. 1 приведен условный пример, отражающий изменение стоимости потребительской корзины по трем товарам.
Табл. 1. Изменение стоимости товаров, входящих в потребительскую корзину
Индекс цен р и индекс инфляции i рассчитываются следующим образом:
р = 
Т.к. i > 0, то это инфляция — повышение общего (среднего) уровня цен в экономике страны. Заметим, что при i
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
http://lektsii.org/14-12865.html
http://natalibrilenova.ru/reshenie-zadach-metodom-gaussa/