Видео урок графический способ решения систем уравнений

Как решать системы уравнений с двумя переменными

Что такое система уравнений с двумя переменными

Системой уравнений в алгебре называется некое условие, смысл которого заключается в одновременном выполнении нескольких уравнений относительно нескольких (либо одной) переменных.

Это значит, что система представляет собой комплекс уравнений. Данные равенства могут содержать одну, две или более переменных. Основным условием понятия «система уравнений» является то, что все эти уравнения выполняются в одно время.

Объединить уравнения в систему можно с помощью фигурной скобки:

У р а в н е н и е 1 У р а в н е н и е 2 У р а в н е н и е 3 …

Графический метод решения

Принцип решения систем уравнений графическим способом заключается в построении графиков для каждого уравнения в общей системе координат. Тогда решения системы соответствуют точкам, в которых данные графики пересекаются. После объяснения решения ответ принято записывать, как координаты этих точек.

Разберем наглядный пример. Предположим, что дана некая система уравнений, решать которую нужно графическим способом. Выполним работу последовательно:

1. Запишем систему.
2. Выразим одну из переменных (пусть это будет у).
3. Построим на координатной прямой графики функций.
4. Найдем точки пересечения графиков.

2 x + 3 y = 12 3 x — y = 7 ⇔ y = 4 — 2 3 x y = 3 x — 7

Заметим, что точка пересечения графиков имеет следующие координаты:

Графический метод решения систем уравнений уступает в точности другим способам. Использовать график целесообразно в том случае, когда в задаче записана система линейных уравнений. Подобные задачи встречаются в средних классах школы. Такие уравнения имеют вид y = a x + b без квадратных членов, а их графики являются прямыми.

Метод подстановки

Алгоритм решения системы уравнений с помощью метода подстановки:

• выражение одной переменной через другие;
• подстановка выражения, которое получилось, в начальные уравнения на место выраженной переменной;
• повторение второго шага до тех пор, пока не будут определены другие переменные.

Рассмотрим последовательность действий на практике. Предположим, что имеется некая система уравнений, которую требуется решить:

2 x + 3 y = 12 3 x — y = 7

Выразим у из второго уравнения:

Выполним подстановку полученного выражения в первое равенство:

2 x + 3 3 x — 7 = 12

Для полученного уравнения с одной переменной несложно найти корни:

2 x + 3 3 x — 7 = 12

2 x + 3 · 3 x — 3 · 7 = 12

2 x + 9 x — 21 = 12

Зная х, выполним подстановку и найдем у:

y = 3 x — 7 = 3 · 3 — 7 = 2 .

Запишем в ответ значения двух переменных.

Ответ: x = 3 ; y = 2 , либо (3;2).

Метод сложения

При сложении левых частей пары (или более) уравнений выражение, полученное в результате, равно сложенным правым частям этих же равенств, согласно формуле:

a = b c = d ⇒ a + c = b + d

В обратную сторону записанное свойство не работает:

a + c = b + d ◃ ≠ ▹ a = b c = d

Таким образом, при решении систем уравнений можно увеличивать обе части уравнения на одинаковое число. Например, сложим первое уравнение с числом с:

a = b c = d ⇒ a + c = b + c

Исходя из того что c=d, можно выполнить замену c на d справа:

a = b c = d ⇒ a + c = b + c ⇒ a + c = b + d .

В качестве примера попробуем решить систему уравнений:

2 x + y = 12 3 x — y = 3

Следуя правилу, суммируем уравнения. В процессе левые части складываем друг с другом. Аналогичным образом поступим с правыми частями равенств. В результате:

2 x + y = 12 3 x — y = 3 ⇒ 2 x ¯ ¯ + y ¯ + 3 x ¯ ¯ — y ¯ = 15 ⇔ 5 x = 15 ⇔ x = 3 .

Получилось избавиться от переменной у. В итоге задача значительно упростилась. Подставим число 3 на место слагаемого с х:

2 x + y = 12 x = 3 ⇔ 2 · 3 + y = 12 x = 3 ⇔ y = 6 x = 3

В следующем примере система уравнений имеет следующий вид:

2 x + 3 y = 13 4 x + 5 y = 23

Заметим, что с помощью сложения задание не получится упростить. В этом случае можно воспользоваться умножением уравнения на какое-либо число, отличное от нуля. Важно выбрать такой множитель, который позволит избавиться от одной из переменных. В этом случае лучше использовать (-2):

2 x + 3 y = 13 · — 2 4 x + 5 y = 23 ⇔ — 4 x — 6 y = — 26 4 x + 5 y = 23

Приступим к сложению:

— 4 x — 6 y = — 26 4 x + 5 y = 23 ⇒ — 4 x — 6 y + 4 x + 5 y = — 26 + 23 ⇔ — y = — 3 ⇔

Выполним подстановку у=3 в первое уравнение:

2 x + 3 y = 13 y = 3 ⇔ 2 x + 9 = 13 y = 3 ⇔ x = 2 y = 3

Задания для самостоятельного решения

Нужно решить систему уравнений:

13 x + 6 y = 7 2 x — 4 y = 6

Выразим х с помощью второго уравнения:

Найти значения переменных:

2 x + 5 y = 10 8 y — 5 x = 57

Из первого равенства выразим х:

2 x + 5 y = 10 2 x = 10 — 5 y

Подставим полученное значение во второе уравнение и запишем ответ.

Дана система уравнений, которую требуется решить:

2 x + 5 y = 10 3 x — 2 y = 1

В данном случае следует умножить первое уравнение на число 2, а второе равенство умножить на число 5:

2 x + 5 y = 10 · 2 3 x — 2 y = 1 · 5 ⇔ 4 x + 10 y = 20 15 x — 10 y = 5

После сложения уравнений остается лишь определить х:

19 x = 25 ⇔ x = 25 19

При подстановке х в какое-либо из двух уравнений можно вычислить у и записать ответ.

Ответ: ( 25 19 ; 28 19 ) .

Требуется найти переменные:

3 y — 4 x = — 13 3 x + 7 y = 56

Здесь следует в первую очередь найти произведение первого уравнения и числа 3, умножить второе уравнение на множитель 4. Далее остается суммировать уравнения и записать ответ.

Нужно решить систему уравнений:

7 x + 3 y = 21 4 y — 5 x = — 15

Множителем для первого уравнения является число 4. Второе уравнение нужно умножить на -3. Полученные равенства следует сложить и записать ответ.

Решить систему уравнений:

6 x — 8 y = — 2 9 x + 10 y = 8

В данном случае предполагается умножение уравнений на дробные числа. Множителем для первого уравнения является дробь 1 4 . Второе уравнение следует умножить на 1 5 :

6 x — 8 y = — 2 · 1 4 9 x + 10 y = 8 · 1 5 ⇔ 6 4 x — 2 y = — 1 2 9 5 x — 2 y = 8 5

Далее выполним сложение:

6 4 x — 2 y = — 1 2 9 5 x — 2 y = 8 5 ⇔ 3 2 x + 9 5 x =-0,5+1,6 ⇔ ⇔ 15 10 x + 18 10 x = 1,1 ⇔ 33 10 x = 1 , 1 ⇔ ⇔ 33 = 11 x x = 3

Путем подстановки определим y:

6 3 — 8 y = — 2 x = 3 ⇔ — 8 y = — 4 x = 3 ⇔ y = 2 x = 3

Найти корни следующих систем уравнений:

2 x + 3 y = 11 3 x + 2 y = 9

3 x — y = 85 5 x + 2 y = 17

x — 3 y = 6 2 y — 5 x = — 4

y 4 — x 5 = 6 x 15 + y 12 = 0

y — x = 5 x + 3 y = 3

Ответ: (1; 3), (17; -34), (0; -2), (-15; 12), (-3; 2).

Урок «Графический способ решения систем уравнений»

Краткое описание документа:

Видеоурок «Графический способ решения систем уравнений» представляет учебный материал для освоения данной темы. Материал содержит общее понятие о решении системы уравнений, а также подробное объяснение на примере, каким образом решается система уравнений графическим способом.

Наглядное пособие использует анимацию для более удобного и понятного выполнения построений, а также разные способы выделения важных понятий и деталей для углубленного понимания материала, лучшего его запоминания.

Видеоурок начинается с представления темы. Ученикам напоминается, что такое система уравнений, и с какими системами уравнений им уже пришлось ознакомиться в 7 классе. Ранее ученикам приходилось решать системы уравнений вида ах+by=c. Углубляя понятие о решении систем уравнений и с целью формирования умения их решать в данном видеоуроке рассматривается решение системы, состоящей из двух уравнений второй степени, а также из одного уравнения второй степени, а второго – первой степени. Напоминается о том, что такое решение системы уравнений. Определение решения системы как пары значений переменных, обращающих ее уравнения при подстановке в верное равенство, выводится на экран. В соответствии с определением решения системы, конкретизируется задача. На экран выведено для запоминания, что решить систему – означает, найти подходящие решения или доказать их отсутствие.

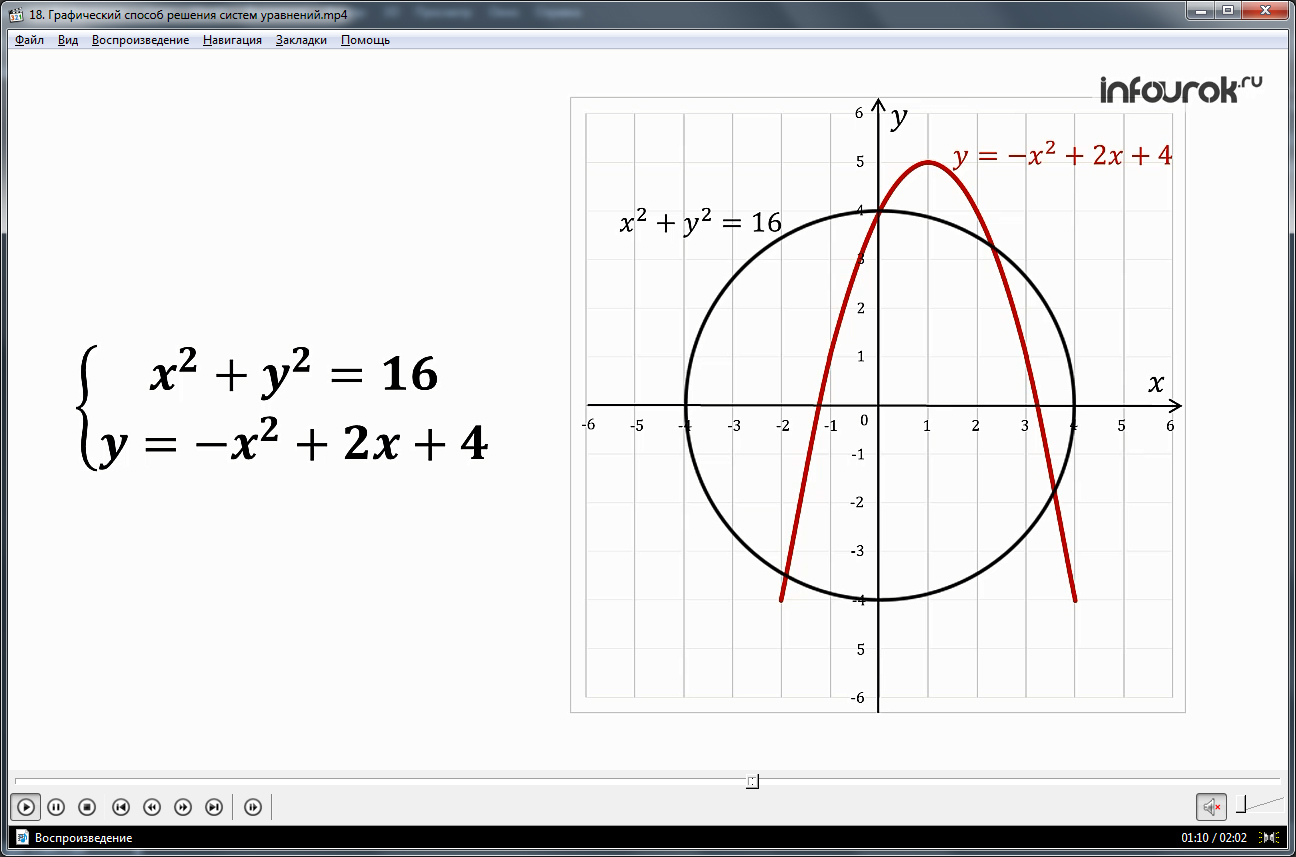
Предлагается освоить графический способ решения некоторой системы уравнений. Применение данного способа рассматривается на примере решения системы, состоящей из уравнений х 2 +у 2 =16 и у=-х 2 +2х+4. Графическое решение системы начинается с построения графика каждого из данных уравнений. Очевидно, графиком уравнения х 2 +у 2 =16 будет окружность. Точки, принадлежащие данной окружности, являются решением уравнения. Рядом с уравнением строится на координатной плоскости окружность радиусом 4 с центром О в начале координат. График второго уравнения представляет собой параболу, ветви которой опущены вниз. На координатной плоскости построена данная парабола, соответствующая графику уравнения. Любая точка, принадлежащая параболе, представляет собой решение уравнения у=-х 2 +2х+4. Объясняется, что решение системы уравнений — точки на графиках, принадлежащие одновременно графикам обоих уравнений. Это значит, что точки пересечения построенных графиков будут являться решениями системы уравнений.

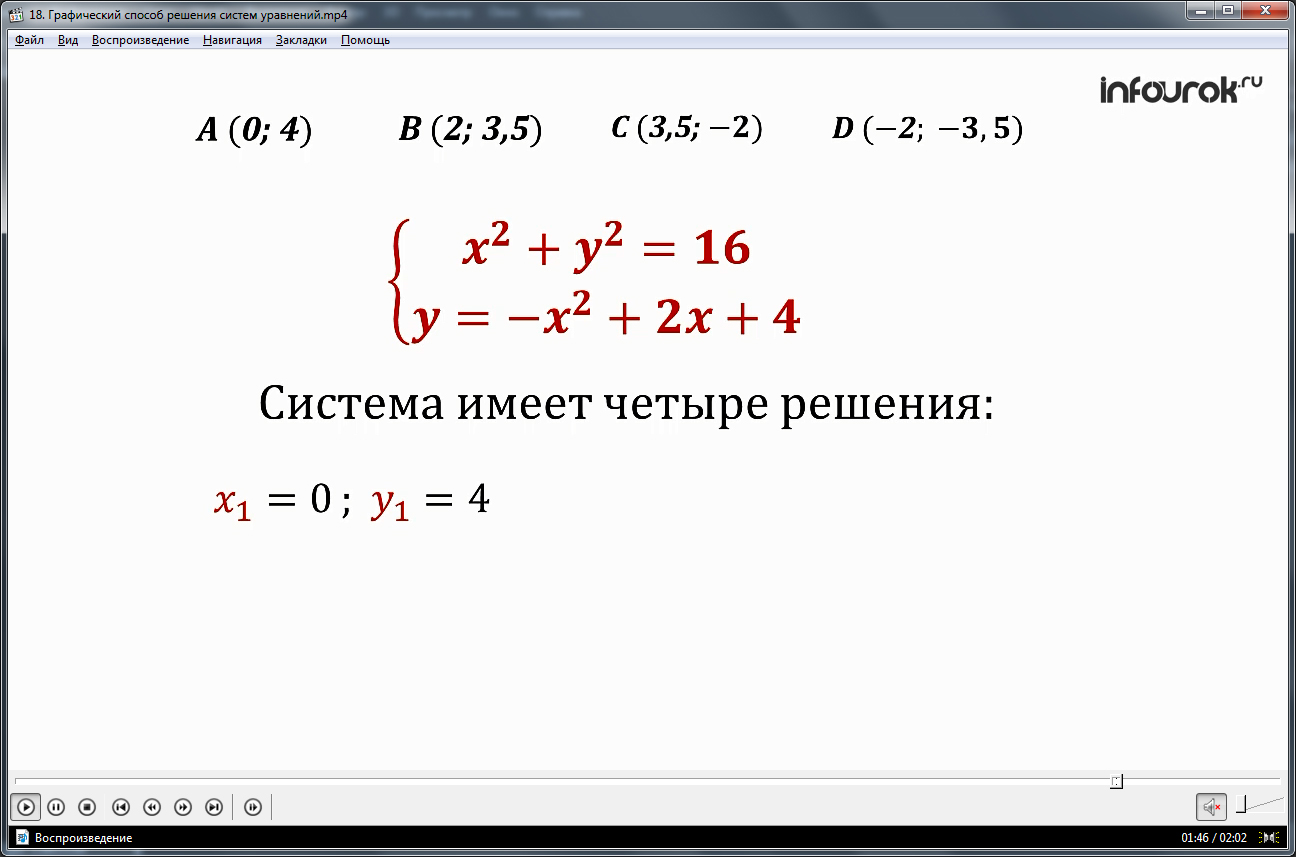
Отмечается, что графический метод состоит в нахождении приближенного значения координат точек, находящихся на пересечении двух графиков, которые отражают множество решений каждого уравнения системы. На рисунке отмечаются координат найденных точек пересечения двух графиков: А[0;4], B[2;3,5], C[3,5;-2], D[-2;-3,5]. Данные точки — решения системы уравнений, найденные графическим способом. Проверить их правильность можно, подставив в уравнение и получив справедливое равенство. После подстановки точек в уравнение, видно, что часть точек дает точное значение решения, а часть представляет приближенное значение решения уравнения: х₁=0, у₁=4; х₂=2, у₂≈3,5; х₃≈3,5, у₃=-2; х₄=-2, у₄≈-3,5.

Видеоурок подробно объясняет суть и применение графического способа решения системы уравнений. Это дает возможность использовать его в качестве видеопособия на уроке алгебры в школе при изучении данной темы. Также материал будет полезен при самостоятельном изучении учениками и может помочь объяснить тему при дистанционном обучении.

Графический метод решения системы уравнений

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На этом уроке мы будем рассматривать решение систем двух уравнений с двумя переменными. Вначале рассмотрим графическое решение системы двух линейных уравнений, специфику совокупности их графиков. Далее решим несколько систем графическим методом.