Видеоурок уравнение касательной графику функции

Уравнение касательной к графику функции. 10-й класс

Класс: 10

Презентация к уроку

Тип урока: изучение нового материала.

Методы обучения: наглядный, частично поисковый.

Цель урока.

Ввести понятие касательной к графику функции в точке, выяснить в чем состоит геометрический смысл производной, вывести уравнение касательной и научить находить его для конкретных функций.
1. Развивать логическое мышление, математическую речь.
2. Воспитывать волю и упорство для достижения конечных результатов.

Оборудование: интерактивная доска, компьютер.

I. Организационный момент

Проверка готовности учащихся к уроку. Сообщение темы урока и целей.

II. Актуализация знаний.

(Вспомнить с учащимися геометрическое определение касательной к графику функции. Привести примеры, показывающие, что данное утверждение не полно.)

Вспомним, что же такое касательная?

“Касательная – это прямая, имеющая с данной кривой одну общую точку”. (Слайд № 2)

Обсуждение правильности данного определения. (После обсуждения, учащиеся приходят к выводу, что данное определение неверно.) Для наглядного доказательства их умозаключения приводим следующий пример.

Рассмотрим пример. (Слайд № 3)

Пусть дана парабола и две прямые , имеющая с данной параболой одну общую точку М (1;1). Проводится обсуждение, почему первая прямая не является к данной параболе касательной (Рис. 1), а вторая является (Рис.2).

На данном уроке, мы с вами должны выяснить, что же такое касательная к графику функции в точке, как составить уравнение касательной?

Рассмотреть основные задачи на составление уравнения касательной.

Для этого, вспомнить общий вид уравнения прямой, условия параллельности прямых, определение производной и правила дифференцирования. (Слайд № 4)

III. Подготовительная работа к изучению нового материала.

IV Изучение нового материала.

Чтобы задать уравнение прямой на плоскости нам достаточно знать угловой коэффициент и координаты одной точки.

Пусть дан график функции . На нем выбрана точка , в этой точке к графику функции проведена касательная (мы предполагаем, что она существует). Найти угловой коэффициент касательной.

Дадим аргументу приращение и рассмотрим на графике (Рис. 3) точку P с абциссой . Угловой коэффициент секущей MP, т.е. тангенс угла между секущей и осью x, вычисляется по формуле .

Если мы теперь устремим к нулю, то точка Р начнет приближаться по кривой к точке М. Касательную мы охарактеризовали как предельное положение секущей при этом приближении. Значит, естественно считать, что угловой коэффициент касательной будет вычисляться по формуле .

Следовательно, .

Если к графику функции y = f (x) в точке х = а можно провести касательную, непараллельную оси у, то выражает угловой коэффициент касательной. (Слайд № 10)

Или по другому. Производная в точке х = а равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке .

Это и есть геометрический смысл производной. (Слайд № 11)

Причем, если :

1. 
2. 
3. .

Выясним общий вид уравнения касательной.

Пусть, прямая задана уравнением . Мы знаем, что . Для вычисления m воспользуемся тем, что прямая проходит через точку . Подставим в уравнение. Получим , т.е. . Подставим найденные значения k и m в уравнение прямой:

– уравнение касательной к графику функции. (Слайд № 12)

Составим уравнение касательной:

1. к параболе в точке (Слайд № 13)
2. к графику функции в точке

Решая эти примеры мы воспользовались очень простым алгоритмом, который заключается в следующем: (Слайд № 15)

1. Обозначим абсциссу точки касания буквой a.
2. Вычислим .
3. Найдем и .
4. Подставим найденные числа , в формулу

Рассмотрим типичные задания и их решение.

№1 Составить уравнение касательной к графику функции в точке .

Решение. Воспользуемся алгоритмом, учитывая, что в данном примере .

1)

2)

3) ;

4) Подставим найденные числа ,, в формулу.

, т.е.

Ответ:

№2 К графику функции провести касательную так, чтобы она была параллельна прямой . (Слайд № 17)

Решение. Уточним формулировку задачи. Требование “провести касательную” обычно означает “составить уравнение касательной”. Воспользуемся алгоритмом составления касательной, учитывая, что в данном примере .

Искомая касательная должна быть параллельна прямой . Две прямые параллельны, тогда и только тогда, когда равны их угловые коэффициенты. Значит угловой коэффициент касательной должен быть равен угловому коэффициенту заданной прямой: .Но . Следовательно: ; .

Из уравнения ,т.е. , находим, что и . Значит, имеются две касательные, удовлетворяющие условию задачи: одна в точке с абсциссой 2, другая в точке с абсциссой -2.

Действуем по алгоритму.

1) ,

2) ,

3)

4) Подставив значения ,, , получим , т.е. .

Подставив значения ,, , получим , т.е.

Ответ: , .

V. Решение задач.

1. Решение задач на готовых чертежах (Слайд № 18 и Слайд № 19)

2. Решение задач из учебника: № 29.3 (а,в), № 29.12 (б,г), № 29.18, № 29.23 (а) (Слайд № 20)

VI. Подведение итогов.

1. Ответьте на вопросы:

• Что называется касательной к графику функции в точке?
• В чем заключается геометрический смысл производной?
• Сформулируйте алгоритм нахождения уравнения касательной?

2. В чем были трудности на уроке, какие моменты урока наиболее понравились?

3. Выставление отметок.

VII. Комментарии к домашней работе

№ 29.3 (б,г), № 29.12 (а,в), № 29.19, № 29.23 (б) (Слайд №22)

Литература. (Слайд 23)

1. Алгебра и начала математического анализа: Учеб. Для 10-11 кл. для учащихся общеобразовательных учреждений (базовый уровень) / Под редакцией А.Г. Мордковича. – М.: Мнемозина, 2009.
2. Алгебра и начала математического анализа: Задачник, Для 10-11 кл. для учащихся общеобразовательных учреждений (базовый уровень) / Под редакцией А.Г. Мордковича. – М.: Мнемозина, 2009.
3. Алгебра и начала анализа. Самостоятельные и контрольные работы для 10-11 классов. / Ершова А.П., Голобородько В.В. – М.: ИЛЕКСА, 2010.
4. ЕГЭ 2010. Математика. Задача В8. Рабочая тетрадь / Под редакцией А.Л.Семенова и И.В.Ященко – M.: Издательство МЦНМО, 2010.

Урок «Уравнение касательной к графику функции»

Краткое описание документа:

Видеоурок «Уравнение касательной к графику функции» демонстрирует учебный материал для освоения темы. В ходе видеоурока представлен теоретический материал, необходимый для формирования понятия об уравнении касательной к графику функции в данной точке, алгоритм нахождения такой касательной, описаны примеры решения задач с использованием изученного теоретического материала.

В видеоуроке используются методы, улучшающие наглядность материала. В представлении вставлены рисунки, схемы, даются важные голосовые комментарии, применяется анимация, выделение цветом и другими инструментами.

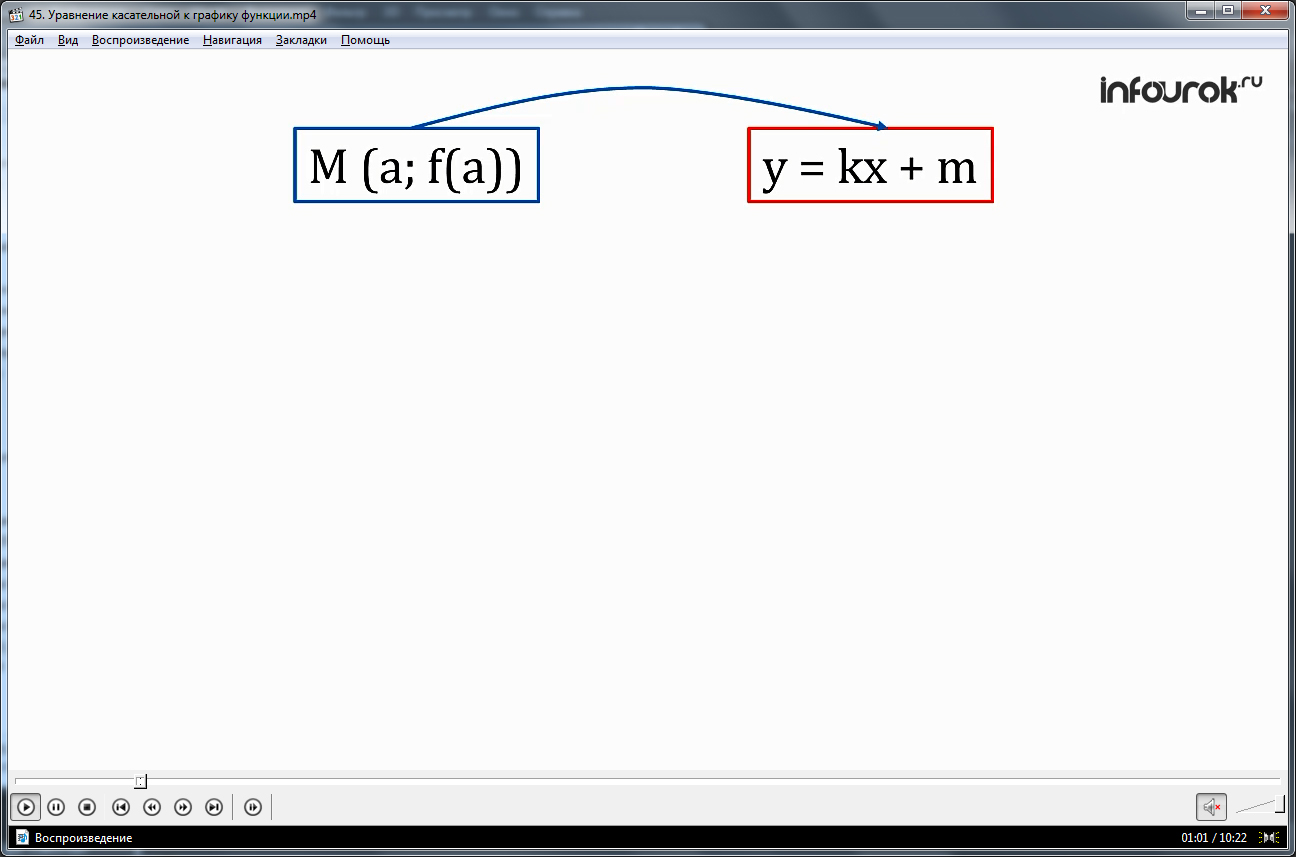
Видеоурок начинается с представления темы урока и изображения касательной к графику некоторой функции y=f(x) в точке M(a;f(a)). Известно, что угловой коэффициент касательной, построенной к графику в данной точке, равен производной функции f΄(a) в данной точке. Также из курса алгебры известно уравнение прямой y=kx+m. Схематично представлено решение задачи нахождения уравнения касательной в точке, которая сводится к нахождению коэффициентов k, m. Зная координаты точки, принадлежащей графику функции, можем найти m, подставив значение координат в уравнение касательной f(a)=ka+m. Из него находим m=f(a)-ka. Таким образом, зная значение производной в данной точке и координаты точки, можно представить уравнение касательной таким образом y=f(a)+f΄(a)(x-a).

Далее рассматривается пример составления уравнения касательной, следуя схеме. Дана функция y=x 2 , x=-2. Приняв а=-2, находим значение функции в данной точке f(a)= f(-2)=(-2) 2 =4. Определяем производную функции f΄(х)=2х. В данной точке производная равна f΄(a)= f΄(-2)=2·(-2)=-4. Для составления уравнения найдены все коэффициенты а=-2, f(a)=4, f΄(a)=-4, поэтому уравнение касательной у=4+(-4)(х+2). Упростив уравнение, получаем у=-4-4х.

В следующем примере предлагается составить уравнение касательной в начале координат к графику функции y=tgx. В данной точке а=0, f(0)=0, f΄(х)=1/cos 2 x, f΄(0)=1. Таким образом, уравнение касательной выглядит у=х.

В качестве обобщения процесс составления уравнения касательной к графику функции в некоторой точке оформляется в виде алгоритма, состоящего из 4 шагов:

• Вводится обозначение а абсциссы точки касания;
• Вычисляется f(a);
• Определяется f΄(х) и вычисляется f΄(a). В формулу уравнения касательной y=f(a)+f΄(a)(x-a) подставляются найденные значения а, f(a), f΄(a).

В примере 1 рассматривается составление уравнения касательной к графику функции у=1/х в точке х=1. Для решения задачи пользуемся алгоритмом. Для данной функции в точке а=1 значение функции f(a)=-1. Производная функции f΄(х)=1/х 2 . В точке а=1 производная f΄(a)= f΄(1)=1. Используя полученные данные, составляется уравнение касательной у=-1+(х-1), или у=х-2.

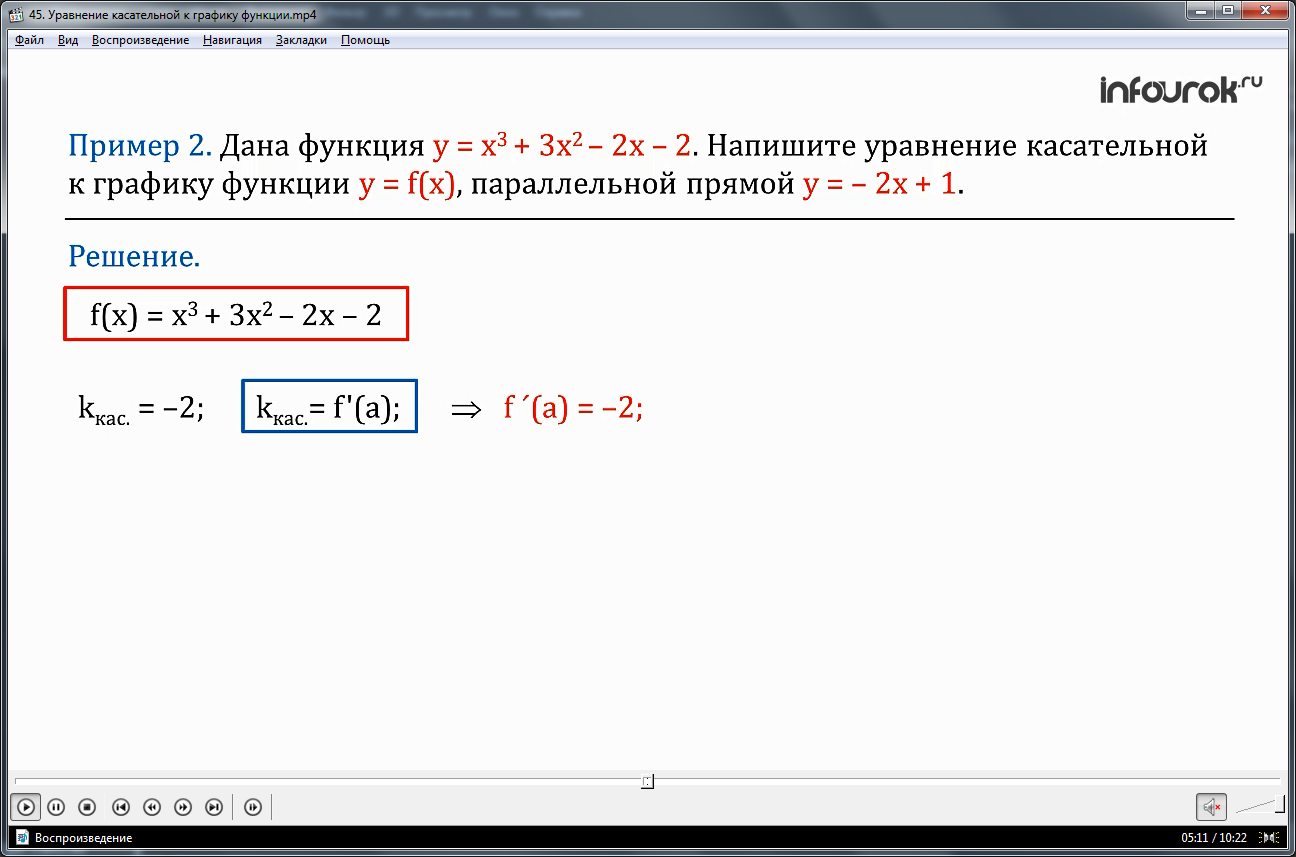
В примере 2 необходимо найти уравнение касательной к графику функции у=х 3 +3х 2 -2х-2. Основное условие – параллельность касательной и прямой у=-2х+1. Сначала находим угловой коэффициент касательной, равный угловому коэффициенту прямой у=-2х+1. Так как f΄(a)=-2 для данной прямой, то k=-2 и для искомой касательной. Находим производную функции (х 3 +3х 2 -2х-2)΄=3х 2 +6х-2. Зная, что f΄(a)=-2, находим координаты точки 3а 2 +6а-2=-2. Решив уравнение, получаем а₁=0, а₂=-2. Используя найденные координаты, можно найти уравнение касательной с помощью известного алгоритма. Находим значение функции в точках f(а₁)=-2, f(а₂)=-18. Значение производной в точке f΄( а₁)= f΄( а₂)=-2. Подставив найденные значения в уравнение касательной, получим для первой точки а₁=0 у=-2х-2, а для второй точки а₂=-2 уравнение касательной у=-2х-22.

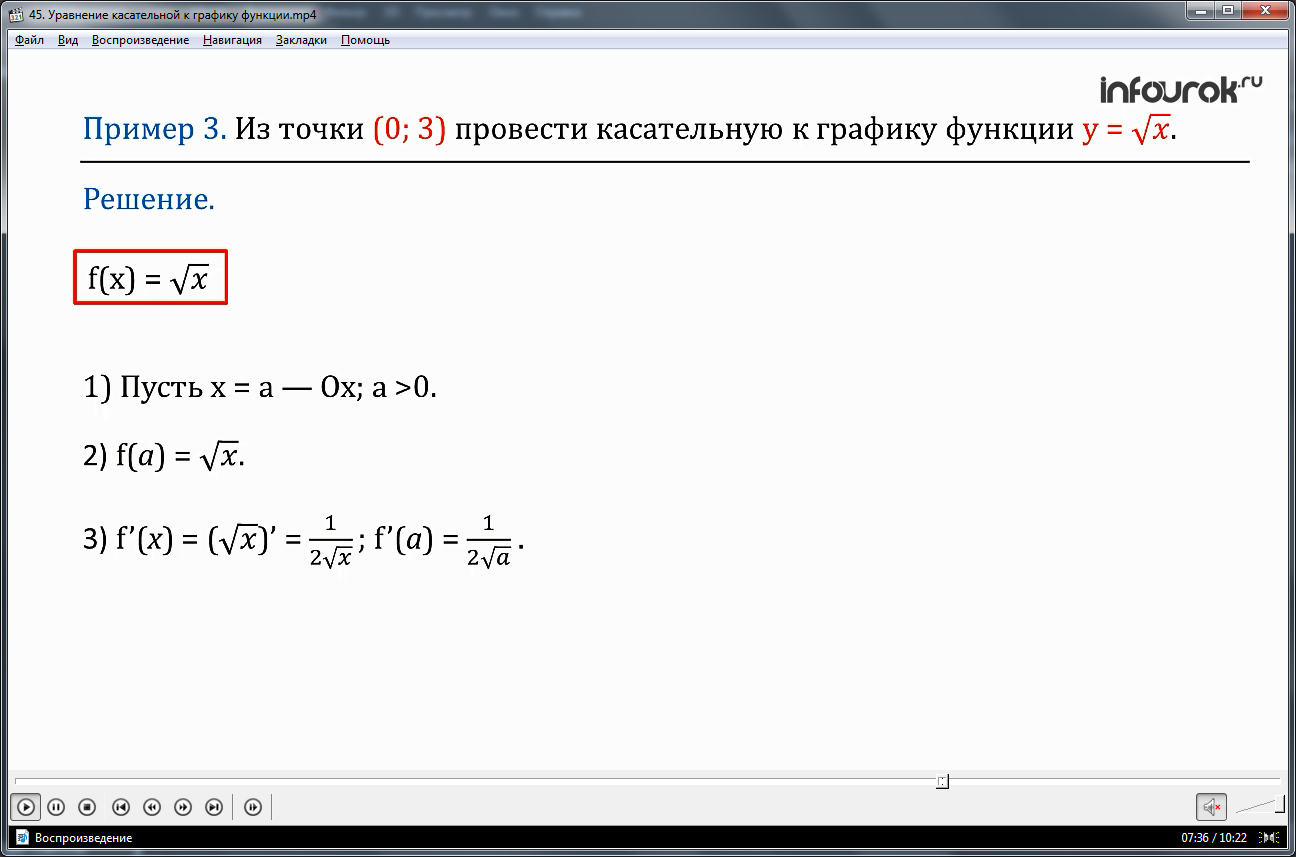
В примере 3 описывается составление уравнения касательной для ее проведения в точке (0;3) к графику функции y=√x. Решение производится по известному алгоритму. Точка касания имеет координаты х=а, где а>0. Значение функции в точке f(a)=√x. Производная функции f΄(х)=1/2√х, поэтому в данной точке f΄(а)=1/2√а. Подставив все полученные значения в уравнение касательной, получаем у=√а+(х-а)/2√а. Преобразовав уравнение, получаем у=х/2√а+√а/2. Зная, что касательная проходит через точку (0;3), находим значение а. Находим а из 3=√а/2. Отсюда √а=6, а=36. Находим уравнение касательной у=х/12+3. На рисунке изображается график рассматриваемой функции и построенная искомая касательная.

Ученикам напоминаются приближенные равенства Δy=≈f΄(x)Δxи f(x+Δx)-f(x)≈f΄(x)Δx. Принимая х=а, x+Δx=х, Δx=х-а, получаем f(х)- f(а)≈f΄(а)(х-а), отсюда f(х)≈f(а)+f΄(а)(х-а).

В примере 4 необходимо найти приближенное значение выражение 2,003 6 . Так как необходимо отыскать значение функции f(х)=х 6 в точке х=2,003, можем воспользоваться известной формулой, приняв f(х)=х 6 , а=2, f(а)= f(2)=64, f΄(x)=6х 5 . Производная в точке f΄(2)=192. Поэтому 2,003 6 ≈65-192·0,003. Вычислив выражение, получаем 2,003 6 ≈64,576.

Видеоурок «Уравнение касательной к графику функции» рекомендуется использовать на традиционном уроке математики в школе. Учителю, осуществляющему обучению дистанционно, видеоматериал поможет более понятно объяснить тему. Видео может быть рекомендовано для самостоятельного рассмотрения учениками при необходимости углубить их понимание предмета.

Нам известно, что если точка М (а; f(а)) (эм с координатами а и эф от а) принадлежит графику функции у =f (x) и если в этой точке к графику функции можно провести касательную, не перпендикулярную к оси абсцисс, то угловой коэффициент касательной равен f'(a) (эф штрих от а).

Пусть даны функция у = f(x) и точка М (a; f(a)), a также известно, что существует f´(a). Составим уравнение касательной к графику заданной функции в заданной точке. Это уравнение, как уравнение любой прямой, не параллельной оси ординат, имеет вид y = kx+m (игрек равный ка икс плюс эм), поэтому задача состоит в отыскании значений коэффициентов k и m.(ка и эм)

Угловой коэффициент k= f'(a). Для вычисления значения m воспользуемся тем, что искомая прямая проходит через точку М(а; f (а)). Это значит, что, если подставить координаты точки М в уравнение прямой, получим верное равенство: f(a) = ka+m, откуда находим, что m = f(a) – ka.

Осталось подставить найденные значения коэффициентов kи mв уравнение прямой:

Нами получено уравнение касательной к графику функции y = f(x) в точке х=а.

Если, скажем, у = х 2 и х= –2 (т.е. а = –2), то f(а) = f(–2) = (–2) 2 =4; f´(x) = 2х, значит, f'(a) = f´(–2) = 2·(–2) = –4. ( то эф от а равно четыре, эф штрих от икс равно два икс, значит эф штрих от а равно минус четыре)

Подставив в уравнение найденные значения a = –2, f(a) = 4, f'(a) = –4, получим: у = 4+(–4)(х+2), т.е. у = –4х–4.

(игрек равен минус четыре икс минус четыре)

Составим уравнение касательной к графику функции у = tgx(игрек равен тангенс икс) в начале координат. Имеем: а = 0, f(0) = tg0=0;

f'(x)= , значит, f'(0) = l. Подставив в уравнение найденные значения а=0, f(a)=0, f´(a) = 1, получим: у=х.

Обобщим наши шаги нахождения уравнения касательной к графику функции в точке х с помощью алгоритма.

АЛГОРИТМ СОСТАВЛЕНИЯ УРАВНЕНИЯ КАСАТЕЛЬНОЙ К ГРАФИКУ ФУНКЦИИ у = f(x):

1) Обозначить абсциссу точки касания буквой а.

2) Вычислить f (а).

3) Найти f´(x) и вычислить f´(a).

Пример 1. Составить уравнение касательной к графику функции у = – в

Решение. Воспользуемся алгоритмом, учитывая, что в данном примере

4) Подставим найденные три числа: а = 1, f(а) = –1, f'(а) = 1 в формулу. Получим: у = –1+(х–1), у = х–2.

Пример 2. Дана функция у = х 3 +3х 2 –2х–2. Записать уравнение касательной к графику функции у= f(х), параллельной прямой у = –2х +1.

Используя алгоритм составления уравнения касательной, учтем, что в данном примере f(x) = х 3 +3х 2 –2х–2, но здесь не указана абсцисса точки касания.

Начнем рассуждать так. Искомая касательная должна быть параллельна прямой у = –2х+1. А параллельные прямые имеют равные угловые коэффициенты. Значит, угловой коэффициент касательной равен угловому коэффициенту заданной прямой: k_кас. = –2. Hok_кас.= f'(a). Таким образом, значение а мы можем найти из уравнения f ´(а) = –2.

Из уравнения f'(а) = –2, т.е. 3а 2 +6а–2 =–2 находим а₁ =0, a₂ =–2. Значит, имеются две касательные, удовлетворяющие условию задачи: одна в точке с абсциссой 0, другая в точке с абсциссой –2.

Теперь можно действовать по алгоритму.

4) Подставив значения a₁= 0, f(a₁) =–2, f'(a₁) = –2 в формулу, получим:

Подставив значения а₂=–2, f(a₂) =6, f'(a₂)= –2 в формулу, получим:

Ответ: у=–2х–2, у=–2х+2.

Пример 3. Из точки (0; 3) провести касательную к графику функции у = . Решение. Воспользуемся алгоритмом составления уравнения касательной, учитывая, что в данном примере f(x) = . Заметим, что и здесь, как в примере 2, не указана явно абсцисса точки касания. Тем не менее, действуем по алгоритму.

1) Пусть х = а — абсцисса точки касания; ясно, что а >0.

4) Подставив значения a, f(a) = , f'(a) = в формулу

По условию касательная проходит через точку (0; 3). Подставив в уравнение значения х = 0, у = 3, получим: 3 = , и далее =6, a =36.

Как видите, в этом примере только на четвертом шаге алгоритма нам удалось найти абсциссу точки касания. Подставив значение a =36 в уравнение, получим: y=+3

На рис. 1 представлена геометрическая иллюстрация рассмотренного примера: построен график функции у =, проведена прямая у = +3.

Нам известно, что для функции y = f(x), имеющей производную в точке х, справедливо приближенное равенство: Δyf´(x)Δx (дельта игрек приближенно равно эф штрих от икс, умноженное на дельта икс)

или, подробнее, f(x+Δx)–f(x) f´(x) Δx (эф от икс плюс дельта икс минус эф от икс приближенно равно эф штрих от икс на дельта икс).

Для удобства дальнейших рассуждений изменим обозначения:

вместо х будем писать а,

вместо х+Δxбудем писать х

вместо Δх будем писать х–а.

Тогда написанное выше приближенное равенство примет вид:

f(x)f(a)+f´(a)(x–a). (эф от икс приближенно равно эф от а плюс эф штрих от а, умноженное на разность икса и а ).

Пример 4. Найти приближенное значение числового выражения 2,003 6 .

Решение. Речь идет об отыскании значения функции у = х 6 в точке х = 2,003. Воспользуемся формулой f(x)f(a)+f´(a)(x–a), учтя, что в данном примере f(x)=x 6 , a = 2,f(a) = f(2) = 2 6 =64; x = 2,003, f'(x) = 6x 5 и, следовательно, f'(а) = f'(2) = 6·2 5 =192.

В итоге получаем:

2,003 6 64+192· 0,003, т.е. 2,003 6 =64,576.

Если мы воспользуемся калькулятором, то получим:

2,003 6 = 64,5781643.

Как видите, точность приближения вполне приемлема.

Уравнение касательной к графику функции

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На уроке рассматривается тема «Уравнение касательной к графику функции». Выводится уравнение касательной к графику функции. Затем, чтобы успешно решать задачи на касательную, будет рассмотрен смысл каждого его элемента.