Видеоуроки по теме показательные уравнения

2. Уравнение вида

В уравнениях этого типа:

а) все степени имеют одинаковые основания

б) коэффициенты при неизвестном в показателе степени равны.

Чтобы решить это уравнение, нужно вынести за скобку множитель в наименьшей степени.

Пример решения уравнения этого типа:

посмотрите в ВИДЕОУРОКЕ.

3. Уравнение вида

Уравнения этого типа отличаются тем, что

а) все степени имеют одинаковые основания

б) коэффициенты при неизвестном в показателе степени разные.

Уравнения такого типа решаются с помощью замены переменных. Прежде чем вводить замену, желательно освободиться от свободных членов в показателе степени. (, , и т.д)

Посмотрите в ВИДЕОУРОКЕ решение уравнения этого типа:

4. Однородные уравнения вида

Отличительные признаки однородных уравнений:

а) все одночлены имеют одинаковую степень,

б) свободный член равен нулю,

в) в уравнении присутствуют степени с двумя различными основаниями.

Однородные уравнения решаются по сходному алгоритму.

Чтобы решить уравнение такого типа, разделим обе части уравнения на (можно разделить на или на )

Внимание! При делении правой и левой части уравнения на выражение, содержащее неизвестное, можно потерять корни. Поэтому необходимо проверить, не являются ли корни того выражения, на которое мы делим обе части уравнения, корнями исходного уравнения.

В нашем случае, поскольку выражение не равно нулю ни при каких значениях неизвестного, мы можем делить на него без опаски. Разделим левую часть уравнения на это выражение почленно. Получим:

Сократим числитель и знаменатель второй и третьей дроби:

, причем 0″ title=»t>0″/> при всех допустимых значениях неизвестного.

Получим квадратное уравнение:

Решим квадратное уравнение, найдем значения 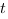, которые удовлетворяют условию 0″ title=»t>0″/>, а затем вернемся к исходному неизвестному.

Смотрите в ВИДЕОУРОКЕ подробное решение однородного уравнения:

При решении этого уравнения будем исходить из того, что 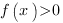0″ title=»f(x)>0″/>

Исходное равенство выполняется в двух случаях:

1. Если , поскольку 1 в любой степени равна 1,

или

2. При выполнении двух условий:

0> >>< >» title=»delim<1><0> >>< >«/>

Посмотрите в ВИДЕОУРОКЕ подробное решение уравнения

Показательные уравнения. 10-й класс

Разделы: Математика

Класс: 10

Учебник: Колягин Ю. М. Алгебра и начала математического анализа. 10 класс. Москва, «Просвещение», 2014.

Урок проведён в универсальном 10-м классе средней общеобразовательной школы.

Цели урока: изучение способов решения показательных уравнений, тренировка в применении полученных знаний при решении заданий по теме, развитие творческой и мыслительной деятельности учащихся, формирование умения чётко и ясно излагать свои мысли, формирование познавательных интересов и мотивов самосовершенствования, воспитание умения работать с имеющейся информацией и культуры труда.

Структура урока

1. Организационный этап. Постановка темы и цели урока

– Прочитайте тему сегодняшнего урока (Приложение 1, слайд № 1)
– «Показательные уравнения».
– Нам это уже известно или это новый вид уравнений?
– Это новый вид уравнений.
– Попробуйте сформулировать цели урока.
– Мы узнаем, какие уравнения называются показательными, изучим способы их решения и будем учиться применять новое знание при решении задач по теме.
Учитель корректирует ответы учащихся.

2. Актуализация знаний. Устная работа (слайд № 3)

1. Подберите корень уравнения 2 х = 32; 3 х = 27; 10 х = 10000
2. Решите уравнение х 2 = 36; х 2 + х = 0; х 2 + 2х + 1 = 0
3. Найдите область значений функции у = π х ; у = (0,5) х ; у = (0,5) |х|
4. Сравните, используя свойства функций, с единицей 2 – 5 ; (0,5) – 3 ; (0,5) 0,5

3. Изучение нового материала (лекция)

Уравнение, в котором неизвестное содержится в показателе степени, считается показательным (слайд № 4). Рассмотрим основные виды показательных уравнений (слайд № 5) (учащиеся записывают названия видов и примеры в тетрадях).

1. Элементарные показательные уравнения. Эти уравнения сводятся к решению уравнений вида а х = а в , где а >0, а ≠ 1. При этом используется свойство степени, которое мы изучали (повторить следствие 2 на стр. 160 учебника). Рассмотрим примеры решения таких уравнений.

Пример 1 (слайд № 6).

(0,0016) 0,2 х + 1 = 25;
5 – 4 (0,2 х + 1) = 52;
– 0,8 х – 4 = 2;
– 0,8 х = 6;
х = – 7,5 .

Пример 2 (слайд №7)

36 · 6 х = 1;
6 2 + х = 60;
2 + х = 0;
х = – 2.

Пример 3 (слайд №8)

81 х · 2 4х = 36;
3 4х · 2 4х = 62;
6 4х = 6 2 ;
4х = 2;
х = 0,5.
Ответ: 0,5.

Пример 4 (слайд № 9)

2 х – 3 = 3 х – 3 ;
х – 3 = 0;
х = 3.
Ответ: 3.

2. Вынесение общего множителя за скобки (слайд № 10). Рассмотрим примеры решения таких уравнений.

2 · 3 х + 1 – 6 · 3 х – 1 – 3 х = 9;
3 х (2 · 3 – 6 · 3 – 1 – 1) = 9;
3 х · 3 = 9;
3 х = 3;
х = 3.
Ответ: 3.

Пример 2 (слайд № 11).

5 2х – 7 х – 5 2х · 17 + 7 х · 17 = 0;
5 2х – 5 2х · 17 = 7 х – 7 х · 17;
5 2х (1 – 17) = 7 х (1 – 17);
– 16· 52х = – 16 · 7х;
5 2х = 7 х ;
25 х = 7 х ;
х= 0.
Ответ: 0.

3. Сведение к квадратному уравнению (слайд № 12). Рассмотрим примеры решения таких уравнений.

9 х – 4 · 3 х = 45;
3 2х – 4 · 3 х – 45 = 0;
Замена 3 х = t, t > 0;
t 2 – 4 t – 45 = 0;
D = 16 +180 = 196;
t₁ = 9,
t₂ = – 5 – не удовлетворяет условию t > 0;
3 х = 9;
3 х = 32;
х = 2;
Ответ: 2.

4. Закрепление изученного материала

– Продолжаем учиться решать показательные уравнения. (Решение всех последующих уравнений записывается на доске с объяснениями, следует вызвать ученика по желанию). Разберём №680(3), 681(1), 682(3), 684(1), 693(2).

5. Обучающая самостоятельная работа с самопроверкой

– Предлагаю вам самостоятельно решить следующие уравнения (слайд № 13), а затем проверить себя самостоятельно с помощью готовых решений (решение уравнений следует заранее заготовить, например, на слайдах, а затем показать учащимся по окончании работы).

1. (0,3) 5 – 2х = 0,09;
2. 225 · 15 2х + 1 = 1;
3. 3 х + 1 – 3 х = 18;
4. 9 х – 26 · 3 х – 27 = 0

Решение № 1 (слайд № 14)

Решение № 2 (слайд № 15)

15 2 · 15 2х + 1 = 150;
152х + 3 = 150;
2х + 3 = 0;
х = – 1,5.
Ответ: – 1,5.

Решение № 3 (слайд № 16)

3 х · 3 – 3 х = 18;
3 х (3 – 1) = 18;
3 х · 2 = 18;
3 х = 9;
3 х = 3 2 ;
х = 2.
Ответ: х = 2.

Решение № 4 (слайд № 17)

3 2х – 26 · 3 х – 27 = 0;
Замена 3 х = t, t > 0;
t 2 – 26 t – 27 = 0;
t₁ = 27,
t₂ = – 1 не удовлетворяет условию t > 0;
3 х = 27; 3 х = 3 3 ; х = 3;
Ответ: 3.

6. Подведение итога урока. Рефлексия

– Итак, подведём итоги проделанной работы. Что нового вы узнали?
– С какими видами показательных уравнений мы познакомились?

7. Домашнее задание (слайд № 18)

2.1.5 Показательные уравнения

Видеоурок 1: Показательные уравнения, часть 1

Видеоурок 2: Показательные уравнения, часть 2

Лекция: Показательные уравнения

Показательные уравнения

Данные уравнения не составят труда для тех, кто знает свойства степенных функций вида у = а х , где основание степени есть число большее нуля, а также не равное единице. Сейчас постараемся вспомнить или выучить их:

1. Областью значения данной функции являются все действительные числа.

2. Областью значения функции являются все положительные числа.

3. Если основание степени находится в пределах между нулем и единицей 0 , то график данной функции будет монотонно убывать. Если же а > 1 , то функция монотонно растет.

4. Отличительной особенностью графика данной функции является то, что он не касается оси ОХ, но стремится к ней на бесконечности. При этом ось ОУ данный график пересекает в точке (0;1), данная точка получается в том случае, если в качестве показателя степени выбрать число «0». А мы знаем, что любое число в данной степени даст единицу.

Обратите внимание на исключение, которое было задано изначально — в основании степени не может стоять единица, поскольку в данном случае при любом показателе степени число изменяться не будет и графиком такой функции будет прямая, параллельная оси ОХ.

Решение показательных уравнений

Существует несколько самых простых способов решить данное уравнение. Однако, обратите внимание, если уравнение не имеет явное сходство с уравнениями, представленными ниже, то его нужно привести к простому виду.

Главным путем решения таких уравнений является приведение его к одному основанию.

• Если одна из частей уравнения равна единицы, а вторая — степенная функция с переменной в показателе степени, то имеем основной алгоритм решения:

а f(x) = 1 => а f(x) = а 0 => f(x) = 0.

Когда уравнение приведено к конечному виду, его следует решать, как любое простейшее алгебраическое уравнение по известным, описанным ранее, способам.

• Если по обеим частям уравнения находятся выражения, в которых основания одинаковы, то имеем право отбросить основания и приравнять показатели степени:

а f(x) = а g(x) => f(x) = g(x).

• Если некоторая степень с переменным показателем равна произвольному числу, то следует воспользоваться основным свойством логарифмов:

а f(x) = b => f(x) = log_ab.