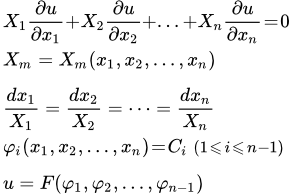Виды частных решений однородных уравнений

Пример частного решения линейного дифференциального уравнения

Рассмотрим тоже самое уравнение, но решим методом вариации произвольной постоянной.
Для нахождения производных C’_i составляем систему уравнений:
C’₁·e -3x ·cos(2x)+C’₂·e -3x ·sin(2x)=0
C’₁(-2·e -3x ·sin(2x)-3·cos(2x)·e -3x ) + C’₂(-3·e -3x ·sin(2x)+2·cos(2x)·e -3x ) = 8*exp(-x)
Выразим C’₁ из первого уравнения:
C’₁ = -c2·sin(2x)/(cos(2x))
и подставим во второе. В итоге получаем:
C’₁ = -4·e 2x ·sin(2x)
C’₂ = 4·cos(2x)·e 2x
Интегрируем полученные функции C’_i:
C₁ = -e 2x ·sin(2x)+cos(2x)·e 2x + C * ₁
C₂ = e 2x ·sin(2x)+cos(2x)·e 2x + C * ₂
Записываем полученные выражения в виде:
C₁ = (-e 2x ·sin(2x)+cos(2x)·e 2x )·cos(2x)·e -3x + C * ₁e -3x ·cos(2x)
C₂ = (e 2x ·sin(2x)+cos(2x)·e 2x )·e -3x ·sin(2x) + C * ₂e -3x ·sin(2x)
или
C₁ = -cos(2x)·e -x ·sin(2x)+cos 2 (2x)·e -x + C * ₁e -3x ·cos(2x)
C₂ = cos(2x)·e -x ·sin(2x)+sin 2 (2x)·e -x + C * ₂e -3x ·sin(2x)
y = C₁ + C₂
Таким образом, общее решение дифференциального уравнения имеет вид:

Пример . y″ + 5y’ + 6 = 12cos(2x)
Cоставляем характеристическое уравнение дифференциального уравнения: r 2 +5 r + 6 = 0
Находим дискриминант: D = 5 2 — 4·1·6 = 1


Корни характеристического уравнения: r₁ = -2, r₂ = -3. Следовательно, фундаментальную систему решений составляют функции: y₁ = e -2x , y₂ = e -3x
Общее решение однородного уравнения имеет вид: y =C₁·e -2x +C₂·e -3x
Найдем частное решение при условии:y(0) = 1, y'(0) = 3
Поскольку y(0) = c₁+c2, то получаем первое уравнение:
c₁+c2 = 1
Находим первую производную: y’ = -3·c₂·e -3·x -2·c1·e -2·x
Поскольку y'(0) = -3·c₂-2·c₂, то получаем второе уравнение:
-3·c₂-2·c₂ = 3
В итоге получаем систему из двух уравнений:
c₁+c2 = 1
-3·c₂-2·c₂ = 3
которую решаем или методом обратной матрицы или методом исключения переменных.
c₁ = 6, c₂ = -5
Тогда частное решение при заданных начальных условиях можно записать в виде: y =6·e -2x -5·e -3x
Рассмотрим правую часть: f(x) = 12·cos(2·x)
Уравнение имеет частное решение вида: y * = Acos(2x) + Bsin(2x)
Вычисляем производные: y’ = -2·A·sin(2x)+2·B·cos(2x); y″ = -4·A·cos(2x)-4·B·sin(2x)
которые подставляем в исходное дифференциальное уравнение: y″ + 5y’ + 6y = (-4·A·cos(2x)-4·B·sin(2x)) + 5(-2·A·sin(2x)+2·B·cos(2x)) + 6(Acos(2x) + Bsin(2x)) = 12·cos(2·x) или -10·A·sin(2x)+2·A·cos(2x)+2·B·sin(2x)+10·B·cos(2x) = 12·cos(2·x)
Приравнивая коэффициенты при одинаковых степенях х, получаем систему линейных уравнений:
-10A + 2B = 0
2A + 10B = 12
СЛАУ решаем методом Крамера:
A = 3 /₁₃;B = 15 /₁₃;
Частное решение имеет вид:
y * = 3 /₁₃cos(2x) + 15 /₁₃sin(2x)
Таким образом, общее решение дифференциального уравнения имеет вид:

Пример 2 . y’’ + y = cos(x)
Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям с постоянными коэффициентами. Решение уравнения будем искать в виде y = e rx . Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами:

r 2 + 1 = 0
D = 0 2 — 4·1·1 = -4

Корни характеристического уравнения:
(комплексные корни):
r₁ = i, r₂ = -i
Следовательно, фундаментальную систему решений составляют функции:
y₁ = e 0 x cos(x) = cos(x)
y₂ = e 0 x sin(x) = sin(x)

Общее решение однородного уравнения имеет вид: y =C₁·cos(x)+C₂·sin(x)

Рассмотрим правую часть: f(x) = cos(x)

Найдем частное решение. Линейное дифференциальное уравнение с постоянными коэффициентами и правой частью вида:
R(x) = e αx (P(x)cos(βx) + Q(x)sin(βx)), где P(x), Q(x) — некоторые полиномы
имеет частное решение
y(x) = x k e αx (R(x)cos(βx) + S(x)sin(βx))
где k — кратность корня α+βi характеристического полинома соответствующего однородного уравнения, R(x), S(x) — полиномы, подлежащие определению, степень которых равна максимальной степени полиномов P(x), Q(x).
Здесь P(x) = 0, Q(x) = 0, α = 0, β = 1.
Следовательно, число α + βi = 0 + 1i является корнем характеристического уравнения кратности k = 1(r₁).

Уравнение имеет частное решение вида:
y * = x (Acos(x) + Bsin(x))
Вычисляем производные:
y’ = sin(x)(B-A·x)+cos(x)(A+B·x)
y″ = cos(x)(2·B-A·x)-sin(x)(2·A+B·x)
которые подставляем в исходное дифференциальное уравнение:
y″ + y = (cos(x)(2·B-A·x)-sin(x)(2·A+B·x)) + (x (Acos(x) + Bsin(x))) = cos(x)
или
2·B·cos(x)-2·A·sin(x) = cos(x)
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
2B = 1
-2A = 0
Следовательно:
A = 0; B = 1 /₂;
Частное решение имеет вид: y * = x (0cos(x) + ½ sin(x)) = ½ x sin(x)

Таким образом, общее решение дифференциального уравнения имеет вид:

Виды однородных уравнений. Системы однородных уравнений.
методическая разработка по теме

Введение

В своей работе я рассмотрела различные методы решения однородных уравнений и систем однородных уравнений, которые чаще всего встречаются при изучении. Представленные методы могут служить опорой для решения разнообразного типа других задач. Решение систем, содержащих два уравнения с двумя переменными второй, четвертой степеней, является не очень простой темой. Но в то же время в некоторых частных случаях такие системы могут быть решены с помощью простых и изящных приёмов. Иногда, посмотрев на уравнение, кажется, что это простое уравнение, но сделав определённые преобразования, мы видим, что это однородное уравнение. Однородные уравнения применяются также и для решения задач по физике. В работе разработана классификация однородных уравнений и систем.

Скачать:

Предварительный просмотр:

Однородные уравнения. Системы однородных уравнений.

Однородные алгебраические уравнения…………………………………………………. 3

Однородные показательные уравнения…………………………………………………….. 8

Однородные логарифмические уравнения………………………………………………. 11

Однородные тригонометрические уравнения…………………………………………. 12

Системы однородных уравнений…………………………………………………………….. 13

Решение систем однородных уравнений графическим методом………….. 22

Список используемой литературы……………………………………………………………. 25

В своей работе я рассмотрела различные методы решения однородных уравнений и систем однородных уравнений, которые чаще всего встречаются при изучении. Представленные методы могут служить опорой для решения разнообразного типа других задач. Решение систем, содержащих два уравнения с двумя переменными второй, четвертой степеней, является не очень простой темой. Но в то же время в некоторых частных случаях такие системы могут быть решены с помощью простых и изящных приёмов. Иногда, посмотрев на уравнение, кажется, что это простое уравнение, но сделав определённые преобразования, мы видим, что это однородное уравнение. Однородные уравнения применяются также и для решения задач по физике. В работе разработана классификация однородных уравнений и систем.

Уравнение называется однородным , если все слагаемые, содержащие неизвестные, имеют одну и ту же степень (показатели степеней разных неизвестных в слагаемом складываются).

1. Однородные алгебраические уравнения

Однородные уравнения 4-й степени. Можно убедиться – делить можно на любой из 3-х слагаемых.

Введем новые неизвестные . Получим уравнение однородное второй степени относительно . Делим обе его части на (легко увидеть, что в случае решений нет) и полагаем . Получаем уравнение c корнями t 1 = – , t 2 = .

В первом случае ;

, это уравнение действительных корней не имеет.

Во втором случае

Ответ: x 1 =3; x 2 =

Положим Тогда уравнение принимает вид: В случае решений нет.

Разделим обе части уравнения на и введем новое неизвестное , получи уравнение c корнями t 1 = , t 2 = –2.

В первом случае ,

Во втором случае ,

Ответ: x 1 = 2; x 2 = 4; x 3 = –1; x 4 = – .

Введем еще одно неизвестное Получим однородное уравнение Его можно решать как обычно, а можно представить в виде следует

Значение x= –3 не удовлетворяет уравнению, а x=5- удовлетворяет.

Если положить то получится уравнение, которое можно было бы назвать «однородным степени », если бы было дано соответствующее определение. Чтобы не иметь дела с дробными показателями, положим:

В первом случае приходим к уравнению откуда делением на находим, что (второй корень уравнения следует отбросить), , так что на промежутке исходное уравнение не имеет корней.

Во втором случае (при ) получаем уравнение откуда Так как то это — корень исходного уравнения.

Однородные уравнения получаются при решении задач.

Задача . Из пункта А в пункт Б выехала машина. Одновременно навстречу ей из пункта Б выехал велосипедист. Через 3 минуты после встречи машина мгновенно поворачивает, едет за велосипедистом, и, догнав его, снова мгновенно поворачивает и прибывает в пункт Б. Если бы машина мгновенно повернула через 1 минуту после встречи, а велосипедист после встречи увеличил бы скорость в 15/7 раза, та машина затратила бы на всю дорогу то же самое время. Найти отношение скоростей велосипедиста и машины.

Пусть x (км/мин) – скорость машины, а y (км/мин) – скорость велосипедиста. Заметим, что на движение машины от пункта А до первой встречи с велосипедистом в первом и втором случае уходит одно и то же время и, что на движение от места первой встречи с велосипедистом до пункта Б в обоих случаях также уходит одинаковое время. Поэтому одно и то же время занимает движение машины от момента первой встречи с велосипедистом до второго прохождения места их первой встречи. Подсчитаем это время в каждом случае.

После встречи с велосипедистом машина ехала 3 минуты в направлении пункта Б. На обратную дорогу до места встречи ей потребуется еще 3 минуты. Велосипедист за это время удалится от места встречи на 6 y км. Машина будет его догонять со скоростью
( x — y ) км/мин, на это у нее уйдет На обратную дорогу до места встречи у нее уйдет также , а всего
мин.

Проводя аналогичные рассуждения, получим:

Приравнивая найденные выражения, получаем уравнение

Это – однородное уравнение второй степени относительно
и Полагая (отношение скорости машины и велосипедиста) и, решая уравнение

находим (отрицательный корень не удовлетворяет условию задачи).

В этой задаче у нас было одно уравнение с двумя независимыми переменными. Такой случай встречается довольно редко, обычно в задачах переменные связаны некоторыми дополнительными соотношениями.

2.Однородные показательные уравнения .

Это однородное уравнение второй степени относительно и . Разделим обе части на . Получим:

Вернемся к замене:

, но не принадлежит

Ответ: решений нет

В ) УНИКАЛЬНОЕ УРАВНЕНИЕ:

Нелегко увидеть, что это уравнение однородное:

Линейные дифференциальные уравнения в частных производных первого порядка

Линейные однородные уравнения в частных производных первого порядка

Пусть X ₁ , X ₂ , . X_n – заданные функции переменных x ₁ , x ₂ , . x_n .

Чтобы решить линейное однородное уравнение в частных производных первого порядка:

необходимо решить систему обыкновенных дифференциальных уравнений (уравнение характеристик):
:
Далее нужно представить решение в виде:
φ ₁( x ₁ , x ₂ , . x_n ) = C ₁ ,
φ ₂( x ₁ , x ₂ , . x_n ) = C ₂ ,
.
φ_{n- 1} ( x ₁ , x ₂ , . x_n ) = C_{n- 1} ,
где C_k – постоянные.
После чего сразу получаем общее решение:
,
где F – произвольная функция от n – 1 аргументов.

Если нужно получить частное решение с определенными граничными условиями, то необходимо подставить значения переменных из граничных условий в общее решение и найти вид функции F .

Линейные неоднородные уравнения в частных производных первого порядка

Пусть X ₁ , X ₂ , . X_{n+ 1} – заданные функции от переменных x ₁ , x ₂ , . x_n и z .

Чтобы решить линейное неоднородное уравнение в частных производных первого порядка:
,
необходимо решить уравнение характеристик:
.
Решение этой системы нужно представить в следующем виде:
φ ₁( x ₁ , x ₂ , . x_n , z ) = C ₁ ,
φ ₂( x ₁ , x ₂ , . x_n , z ) = C ₂ ,
.
φ_n ( x ₁ , x ₂ , . x_n , z ) = C_n .
После чего сразу получаем общий интеграл в неявном виде:

где F – произвольная функция. Также общий интеграл можно представить в различных вариантах, например:
φ ₁ = F ( φ ₂ , φ ₃ , . φ_n ) ,
φ ₂ = F ( φ ₁ , φ ₃ , . φ_n ) ,
и т. д.

Примеры решений линейных уравнений в частных производных первого порядка

Однородное уравнение

Найти общее решение линейного однородного уравнения в частных производных первого порядка и решить задачу Коши с указанным граничным условием:
,
при .

Это линейное однородное уравнение в частных производных первого порядка. Составляем уравнение характеристик:

Это уравнение характеристик содержит три уравнения:
;
;
.
Нам нужно выбрать и решить любые два из них. Тогда третье будет выполнено автоматически.

Выбираем и решаем первое уравнение:

Здесь переменные уже разделены, интегрируем:

Интегралы табличные,

Потенцируем:

Отсюда

Подставим во второе уравнение:

Или:

Это линейное уравнение. Решаем с помощью интегрирующего множителя. Умножим на x -1 и преобразуем:

Интегрируем:

Подставим полученное ранее выражение C₁ = x y 2 :

Итак, мы нашли два интеграла уравнения характеристик:

Общее решение исходного уравнения в частных производных имеет вид:

где F — произвольная функция от двух аргументов F(φ₁, φ₂) . Найдем ее вид из граничного условия
при .

Рассматриваем решение на границе.
Положим x y = –1 :

Отсюда

На границе
.

Итак, мы нашли, что на границе функция F имеет вид:
F ( φ ₁ , φ ₂ ) = φ ₁ φ ₂ .
Такой же вид она имеет и во всей области
Подставляя
;
,
получаем частное решение исходного уравнения в частных производных с заданным граничным условием:

Общее решение:

где F — произвольная функция от двух аргументов F ( φ ₁ , φ ₂ ) .

Неоднородное уравнение

Найти поверхность, удовлетворяющую данному уравнению
,
и проходящую через данную окружность x + y + z = 0 , x 2 + y 2 + z 2 = a 2 .

Это линейное неоднородное уравнение в частных производных первого порядка. Составляем уравнение характеристик:

Оно содержит три уравнения:
;
;
.
Нам нужно выбрать и решить любые два из них. Тогда третье удовлетворится автоматически. Выбираем первое и второе уравнения.

Решаем уравнение:

Умножаем на 2 z и интегрируем:

Интегралы табличные,

Потенцируем:

Отсюда
x = C ₁ y

Подставим во второе уравнение:

Или:

Замечаем, что , тогда

Это линейное уравнение. Решаем с помощью интегрирующего множителя. Разделим на y 2 и преобразуем:

Интегрируем:

Подставим полученное ранее выражение и преобразуем:

Итак, мы нашли два интеграла уравнения характеристик:

Для удобства дальнейших вычислений заметим, что функция от постоянной также является постоянной. Поэтому запишем интегралы в виде:

Общий интеграл исходного уравнения в частных производных имеет вид:
F ( φ ₁ , φ ₂) = 0
Но, поскольку F — произвольная функция от двух аргументов, то общий интеграл можно записать также в виде:
φ ₁ = F ( φ ₂) ,
где F — произвольная функция от одного аргумента.

Найдем вид этой функции, рассматривая решение на границе.
На границе, x 2 + y 2 + z 2 = a 2 , .
Из уравнения x + y + z = 0 , z = – ( x + y ) . Подставим в x 2 + y 2 + z 2 = a 2 и преобразуем:
x 2 + y 2 + ( x + y ) 2 = a 2
x 2 + y 2 + x 2 + 2 xy + y 2 = a 2
2 x 2 + 2 xy + 2 y 2 = a 2
Разделив на y 2 , имеем

Итак, мы нашли, что на границе:

.
Подставим в выражение общего интеграла:
φ ₁ = F ( φ ₂)
.
Сделаем подстановку
:
.

Итак, мы нашли, что на границе функция F имеет вид:
.
Такой же вид она имеет и во всей области, тогда
.
Подставляем выражения для φ₁ и φ₂ :

.
Умножим на a 2 y 2 .

Автор: Олег Одинцов . Опубликовано: 23-09-2014