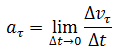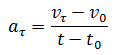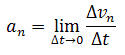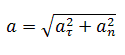Виды и уравнения криволинейного движения

Криволинейное движение

В зависимости от формы траектории движение можно подразделять на прямолинейное и криволинейное. Чаще всего можно столкнуться с криволинейными движениями, когда траектория представлена в виде кривой. Примером такого вида движения является путь тела, брошенного под углом к горизонту, движение Земли вокруг Солнца, планет и так далее.

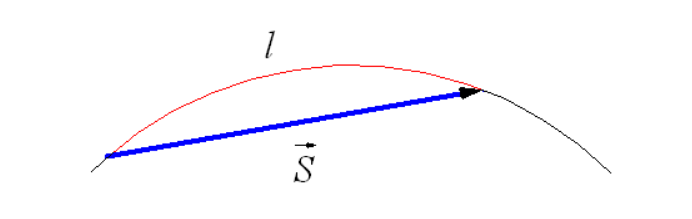
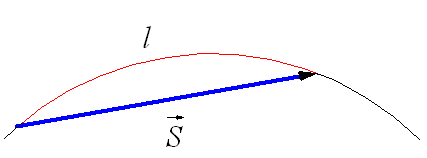
Рисунок 1 . Траектория и перемещение при криволинейном движении

Мгновенная скорость при криволинейном движении

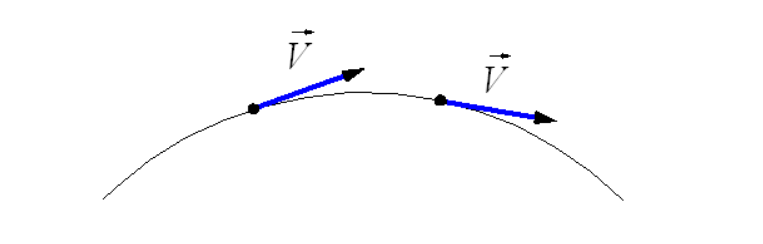
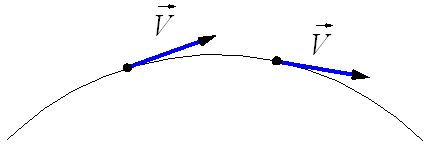
Криволинейным движением называют движение, траектория которого представляет собой кривую линию. Если тело движется по криволинейной траектории, то вектор перемещения s → направлен по хорде, как показано на рисунке 1 , а l является длиной траектории. Направление мгновенной скорости движения тела идет по касательной в той же точке траектории, где в данный момент располагается движущийся объект, как показано на рисунке 2 .

Рисунок 2 . Мгновенная скорость при криволинейном движении

Криволинейное движение материальной точки называют равномерным тогда, когда модуль скорости постоянный (движение по окружности), и равноускоренным при изменяющемся направлении и модуле скорости (движение брошенного тела).

Криволинейное движение всегда ускоренное. Это объясняется тем, что даже при неизмененном модуле скорости, а измененном направлении, всегда присутствует ускорение.

Для того чтобы исследовать криволинейное движение материальной точки, применяют два метода.

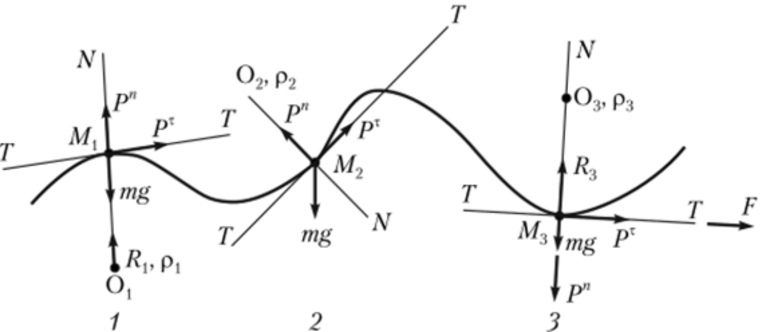
Путь разбивается на отдельные участки, на каждом из которых его можно считать прямолинейным, как показано на рисунке 3 .

Рисунок 3 . Разбиение криволинейного движения на поступательные

Теперь для каждого участка можно применять закон прямолинейного движения. Такой принцип допускается.

Разбиение на движения по дугам

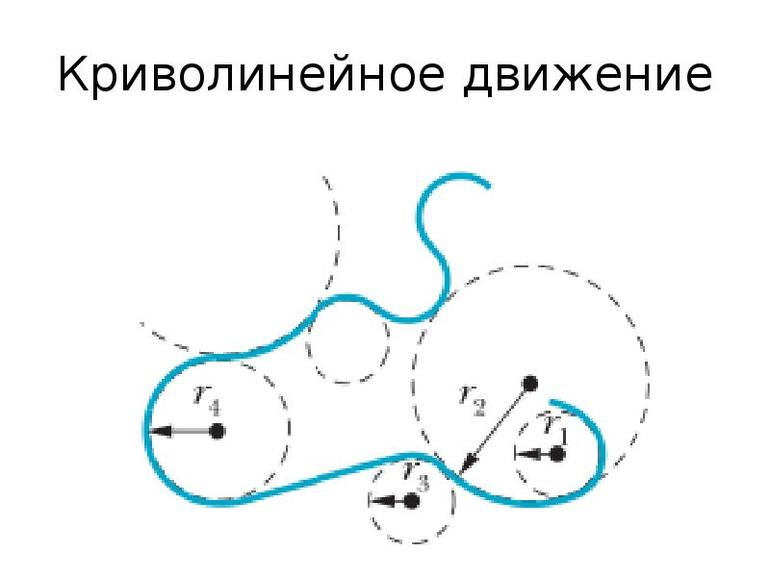
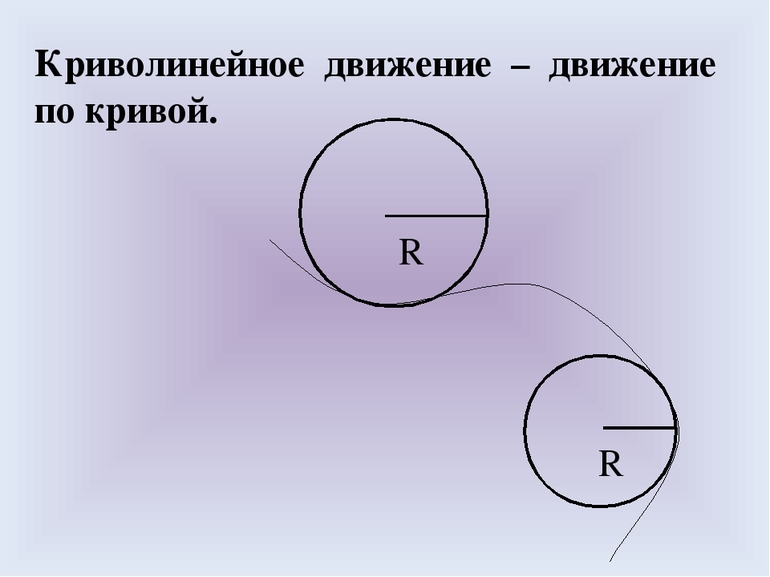
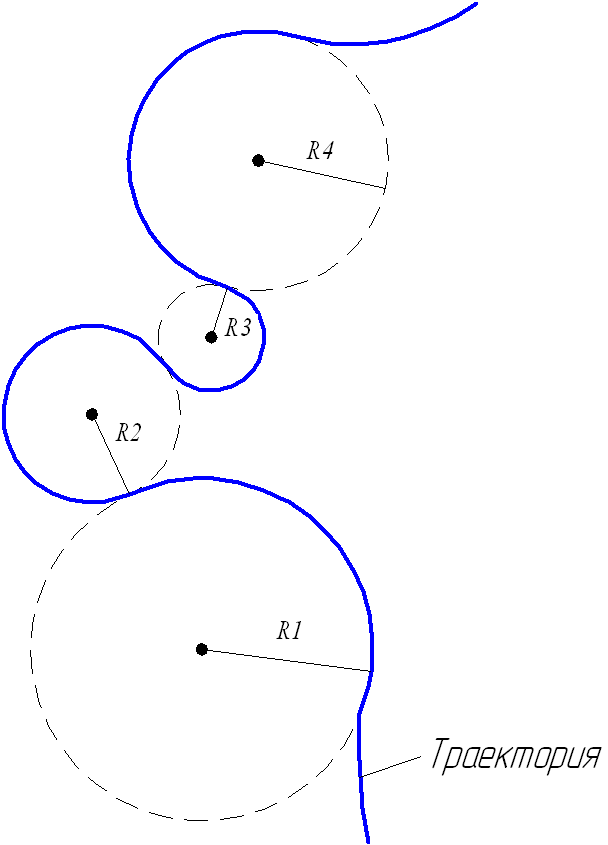
Самым удобным методом решения считается представление пути в качестве совокупности нескольких движений по дугам окружностей, как показано на рисунке 4 . Количество разбиений будет намного меньше, чем в предыдущем методе, кроме того, движение по окружности уже является криволинейным.

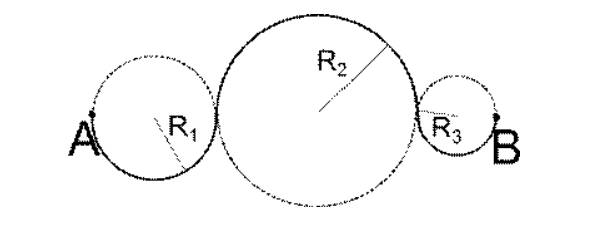
Рисунок 4 . Разбиение криволинейного движения на движения по дугам окружностей

Для записи криволинейного движения необходимо уметь описывать движение по окружности, произвольное движение представлять в виде совокупностей движений по дугам этих окружностей.

Исследование криволинейного движения включает в себя составление кинематического уравнения, которое описывает это движение и позволяет по имеющимся начальным условиям определить все характеристики движения.

Дана материальная точка, движущаяся по кривой, как показано на рисунке 4 . Центры окружностей O 1 , O 2 , O 3 располагаются на одной прямой. Необходимо найти перемещение
s → и длину пути l во время движения из точки А в В .

Решение

По условию имеем, что центры окружности принадлежат одной прямой, отсюда:

s → = R 1 + 2 R 2 + R 3 .

Так как траектория движения – это сумма полуокружностей, то:

A B = π R 1 + R 2 + R 3 .

Ответ: s → = R 1 + 2 R 2 + R 3 , l

A B = π R 1 + R 2 + R 3 .

Дана зависимость пройденного телом пути от времени, представленная уравнением s ( t ) = A + B t + C t 2 + D t 3 ( C = 0 , 1 м / с 2 , D = 0 , 003 м / с 3 ) . Вычислить, через какой промежуток времени после начала движения ускорение тела будет равно 2 м / с 2

Криволинейное движение

Криволинейное движение – это движение, траектория которого представляет собой кривую линию (например, окружность, эллипс, гиперболу, параболу). Примером криволинейного движения является движение планет, конца стрелки часов по циферблату и т.д. В общем случае скорость при криволинейном движении изменяется по величине и по направлению.

Криволинейное движение материальной точки считается равномерным движением, если модуль скорости постоянен (например, равномерное движение по окружности), и равноускоренным, если модуль и направление скорости изменяется (например, движение тела, брошенного под углом к горизонту).

Рис. 1.19. Траектория и вектор перемещения при криволинейном движении.

При движении по криволинейной траектории вектор перемещения направлен по хорде (рис. 1.19), а l – длина траектории. Мгновенная скорость движения тела (то есть скорость тела в данной точке траектории) направлена по касательной в той точке траектории, где в данный момент находится движущееся тело (рис. 1.20).

Рис. 1.20. Мгновенная скорость при криволинейном движении.

Криволинейное движение – это всегда ускоренное движение. То есть ускорение при криволинейном движении присутствует всегда, даже если модуль скорости не изменяется, а изменяется только направление скорости. Изменение величины скорости за единицу времени – это тангенциальное ускорение:

Где v_τ, v₀ – величины скоростей в момент времени t₀ + Δt и t₀ соответственно.

Тангенциальное ускорение в данной точке траектории по направлению совпадает с направлением скорости движения тела или противоположно ему.

Нормальное ускорение — это изменение скорости по направлению за единицу времени:

Нормальное ускорение направлено по радиусу кривизны траектории (к оси вращения). Нормальное ускорение перпендикулярно направлению скорости.

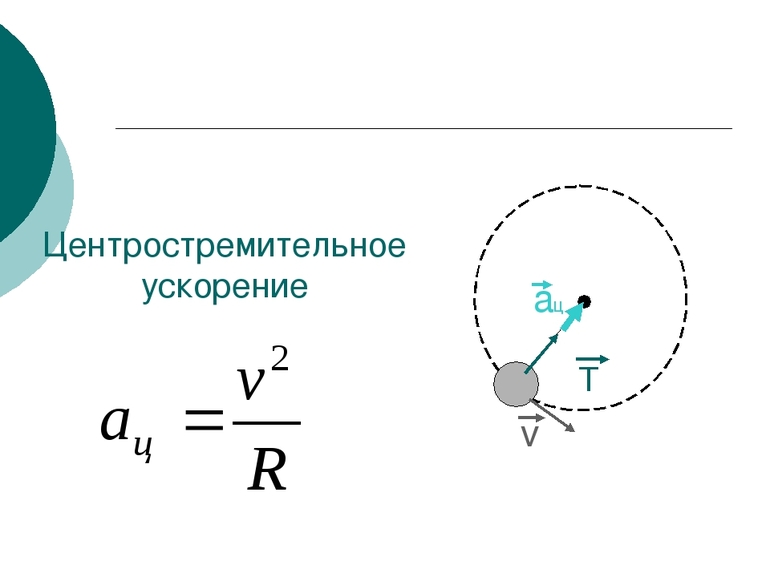
Центростремительное ускорение – это нормальное ускорение при равномерном движении по окружности.

Полное ускорение при равнопеременном криволинейном движении тела равно:

Движение тела по криволинейной траектории можно приближённо представить как движение по дугам некоторых окружностей (рис. 1.21).

Рис. 1.21. Движение тела при криволинейном движении.

Криволинейное движение — общая характеристика, формулы и примеры

Общие сведения

В физике даётся вполне однозначное определение движению. Под ним понимают изменение положения физической точки в пространстве по отношению с другими объектами. Считается, что любое тело состоит из совокупности точек, перемещающихся одинаково по отношению друг к другу. Поэтому любой объект принято обозначать в виде элементарной точки.

Кинематика не изучает, почему движение таково, а рассматривает только путь перемещения. С точки зрения физики, криволинейное движение — это путь, пройденный материальной точкой по кривой траектории. Если же траектория прямая, то изменение положения называется прямолинейным.

Криволинейное движение — это всегда ускоренное перемещение. Оно может быть:

• Равномерным. В этом случае скорость перемещения по модулю остаётся постоянной на всём прошедшем расстоянии. Например, движение по окружности.
• Равноускоренным. Признаком такого движения является изменение скорости и направления. Например, брошенное тело под углом.

Основной характеристикой понятия является вектор перемещения. Обозначается он латинской буквой S со стрелочкой вверху. Направлен он всегда по хорде. Кроме вектора, передвижение по кривой линии определяется тангенциальным и нормальным ускорением.

В первом случае характеристика обозначает изменение величины скорости в единицу времени: at = lim Δv / Δt, где: v — начальная скорость в момент времени t0 + Δt. Тангенциальное ускорение может как совпадать по направлению со скоростью, так и быть ей противоположной.

Нормальным ускорением называют характеристику, перпендикулярную направлению скорости: an = V 2 / r, где: r — радиус окружности. Оно всегда совпадает с радиусом кривизны пути. Подвидом такого ускорения является центростремительная сила. Проявляется она при равномерном перемещении по окружности.

Таким образом, если движение является криволинейным, то вектора скорости и ускорения не лежат на одной прямой. Из простых примеров криволинейного движения можно выделить: течение воды в реке, перелёт на самолёте, катание на колесе обозрения.

Центростремительное ускорение

Если движение равномерное, но происходит оно по кривой, всё равно будет фиксироваться ускорение точки. Это происходит из-за того, что ускорение определяется как изменение скорости к промежутку времени. Поэтому если точка движется равномерно, то это значит, что модуль скорости остаётся одинаковым, но направление вектора изменяется. То есть будет справедливо записать: v = v0, но v ≠ v0. Можно сделать вывод, что изменение скорости существует, если Δv ≠ 0, при этом ускорение тоже не равно нулю: a ≠ 0.

Рассмотрим самый простой вид криволинейного перемещения. Существует история, что ещё во времена Аристотеля древние греки считали окружность идеальной линией. Из-за этого исторического факта астрономам приходилось объяснять движение планет, как комбинацию перемещений космических тел по окружности.

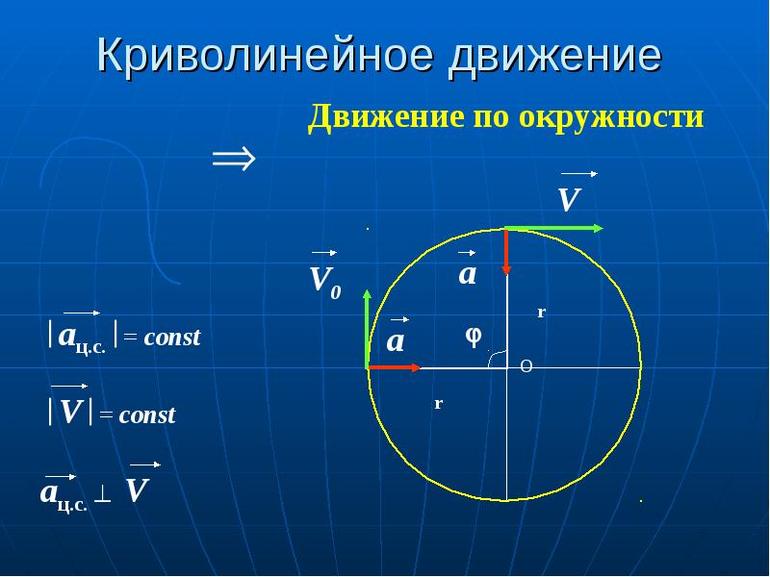
Можно представить тело, изменяющее своё положение по окружности. Траектория перемещения в декартовой системе координат будет выглядеть в виде полусферы. Пусть за её центр будет принята точка O. Тело движется равномерно. В какой-то момент времени его скорость будет V0. Её вектор направлен по касательной и совпадает по направлению с перемещением тела. Через некоторое время объект переместится в другую точку. Его скорость по-прежнему останется направленной по касательной, при этом модуль не изменится. То есть V = V0, но вектора их неравны: V ≠ V0.

Пусть стоит задача — найти равномерное движение по окружности. Иными словами, определить направление вектора и вычислить его модуль. В первую очередь необходимо узнать, куда же направлен вектор ускорения. Чтобы ответить на этот вопрос, нужно опираться на исходную формулу: a = Δv / Δt. Отсюда можно сделать вывод, что куда будет направлен вектор V, туда будет направлено и ускорение a.

Для наглядности можно построить вектор изменения скорости частицы, движущейся по рассматриваемой траектории. Чтобы построить график, описывающий ситуацию, нужно перенести V0 параллельно вектору V к его началу. Соединив два свободных конца перпендикуляром, получится треугольник. По правилу вычитания векторов можно получить вектор изменения скорости: Δv = V — V0. Направлен он будет сверху вниз.

Так как V0 направлен по касательной перпендикулярно радиусу, при этом угол треугольника при основании стремится к нулю, можно утверждать, что Δv перпендикулярен V. Значит, и вектор ускорения перпендикулярен V. Отсюда следует, что вектор ускорения направлен к центру окружности, поэтому его и называют центростремительным ускорением.

Движение по произвольной кривой

Рассмотрим простейший случай равномерного перемещения. Можно представить ситуацию, что если руль автомобиля держать неподвижно, то он будет ехать по прямой или по окружности. В реальной ситуации при езде всё время приходится поворачивать руль автомобиля, то есть в каждый момент времени происходит перемещение по окружности. При этом с каждым поворотом колеса управления радиус окружности изменяется. В данный момент времени он всегда совпадает с траекторией движения и называется радиусом кривизны траектории.

На графике движения можно отметить несколько точек. В одной из них скорость будет равняться V1. Немного дальше пройденное расстояние изменится, но скорость останется той же. Поменяется и направление V2. Через определённое время скорость будет равняться V3. Это движение равномерное.

Относительно точки V1 можно построить касающуюся её окружность с центром r1. По аналогии движения за рулём, это то же самое, что в рассматриваемой точке зафиксировать поворот управления на постоянный угол. Для V2 центр радиуса находится в точке r2, а V3 в r3.

В любом из этих трёх случаев происходит движение по окружности. То есть криволинейное движение произвольной формы — это перемещение по окружности любого радиуса. Если же радиус изменяется, то в любой момент меняется и центростремительное ускорение. Но при этом направление всегда совпадает с радиусом. Самое большое ускорение будет в том месте, где радиус самый маленький, и наоборот. Таким образом можно утверждать, что всякий раз ускорение будет перпендикулярно скорости при равномерном движении.

Кроме центростремительного ускорения, важными характеристиками, описывающими движение, являются следующие величины:

• Период. Показывает, за сколько времени точка совершит один оборот: T = t /n. Где t — время, за которое происходит определённое число оборотов, равное n.
• Частота. Определяет, сколько оборотов совершенно за единицу времени: λ = n / t.
• Угловая скорость. Является отношением угла поворота радиуса ко времени, за который произошёл поворот: W = φ / Δt = 2 * p / T = V / r.

Это основные формулы для криволинейного движения, использующиеся при решении задач. Кроме того, в заданиях используется связь между линейной и угловой скоростями: v = w * r, а также формула полного ускорения: a = at + an.

Решение простых задач

Виды движения изучаются на уроках физики в седьмом классе средней школы. На них ученикам объясняют понятия поступательного и равномерного движения, даются необходимые уравнения. Решение задач на уроках необходимо для закрепления пройденного материала и реального понимания ситуаций, при которых используются знания о видах перемещения.

Вот некоторые типы заданий, часто встречающиеся в различных вариантах у учащихся при сдаче ими тестов или написании контрольных работ:

1. Линейная скорость точек рабочей поверхности наждачного круга диаметром 300 мм не должна превышать 35 метров в секунду. Допустима ли посадка круга на вал электродвигателя, совершающего обращение со скоростью 1400 оборотов в минуту? Согласно условию, необходимо найти, как связаны между собой V1 c Vmax. То есть линейную скорость и частоту вращения. Для расчёта необходимо использовать формулу связи скоростей: v = w * r. Так как поверхность абразива плоская, то радиус его будет равняться: r = d / 2. Подставив все исходные данные, можно записать: v = 2 * p * n / 2 = p * n * d = 3,14 * 1400 * 1/60с * 0,3 м = 22 м/с. Следовательно, из полученного значения можно сделать вывод, что посадка допустима.
2. Какова линейная скорость точек земной поверхности на широте 46,5 0 при суточном вращении? Радиус Земли принять равным 6400 км. Другими словами, нужно выяснить линейную скорость. Широта рассчитывается вдоль меридиана и, по сути, это угол, измеряемый между двумя точками. Одна из них находится на экваторе, а другая — в указанном месте. Между радиусами, проведёнными из этих точек, угол составляет φ. Решить поставленную задачу можно, используя формулы: v = w * r и w = 2 * p / T. Следует учесть, что радиус, соответствующий 46,5 0, будет меньше радиуса Земли. Для того чтобы найти нужное значение, необходимо построить виртуальный треугольник и, используя тригонометрические формулы, записать, что cos φ = r / R. Учитывая, что направлена мгновенная скорость при криволинейном движении к центру, формула будет иметь вид: V = (2 * p / T) * R * cos φ = (6,28 * 6400 * 10 3 * cos 46,5 0 ) / 24 * 3,600 c = 465 * 0,69 м/с = 320 м/с.

Таким образом решать задачи на нахождение различных параметров при криволинейном движении без учёта его вызвавшей причины несложно. При этом следует правильно определить тип движения и знать основные формулы.

Пример сложного уровня

В большей мере такого уровня задачи являются поучительными, так как они используются для реальных случаев. Например, при расчётах работы различных технических установок. Вот одна из них.

Пусть движение от шкива один к шкиву четыре передаётся при помощи двух временных передач. Найти частоту вращения в оборотах в минуту и угловую скорость шкива четыре, если шкив один делает 1200 об/мин, а радиусы шкивов: R1 — 8 см, R2 — 32 см, R3 — 11 см, R4 — 55 см, при этом они жёстко укреплены на одном валу. Передающие ремни принять идеальными.

Для решения этой задачи нужно вначале определить направление вращения. Из условия задачи следует, что первый шкив будет вращаться в другую сторону по сравнению с остальными тремя. Для того чтобы найти угловую скорость последнего ролика, нужно будет последовательно определить параметры предшествующих ему шкивов.

Линейная скорость точек движения на ролике первого и второго шкива одинакова. Это следует из того, что ремни идеальные, не проскакивают и не растягиваются. Таким образом будет справедливо записать: V1 = V2. Так как w1 * r1 = w2 * r2, можно составить отношение: r1 / r2 = w1 / w2 или r1 / r2 = 2 * p * n2 / 2 * p * n1. То есть отношение примет вид: r1 / r2 = n2 / n1.

Так как третий шкив закреплён жёстко на валу со вторым, то образованную систему можно считать одним твёрдым телом. Применительно к нему можно говорить об общей угловой скорости или одинаковой частоте вращения. Получается, что n3 = n2. Тогда можно записать: n3 = n1 = r1 / r2.

На следующем шаге необходимо определить линейную скорость на четвёртом ролике. Из условия известно, что V3 = V4, так как их соединение идеальное. Это значит, что можно связать скорости третьего и четвёртого шкива с частотами: V4 = 2 *p * n4 * r4; V3 = 2 * p * n3. Из полученного равенства нужно выразить n4. Оно будет равняться: n4 = n3 * r3 / r4. В эту формулу необходимо подставить n3 и получить итоговую формулу: n4 = n1 * (r1 * r3) / (r2 * r4).

Теперь нужно подставить исходные данные и выполнить расчёт. При этом переходить в систему СИ нет необходимости: n1 = 1200 об/мин * (8 * 11) / (32 * 55) = 1200 * 1 / 20 об/мин = 60 об/мин. Для того чтобы найти угловую скорость, частоту необходимо умножить на 2p. При этом учесть, что угловая скорость измеряется в радианах в секунду. Поэтому w4 = 2 * p * n4 = 6, 28 * 1 = 6,28 рад/сек. Интересной особенностью является то, что частота вращения первого шкива в двадцать раз больше четвёртого. Задача решена.