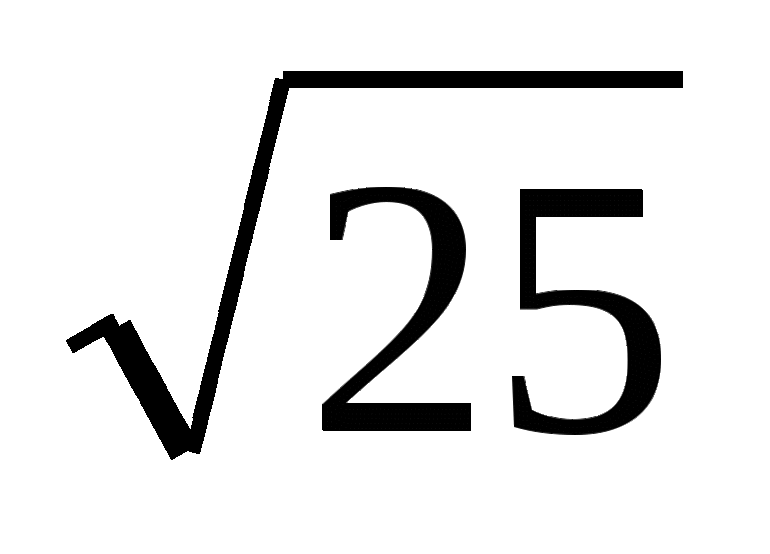Линейные уравнения с параметром
Рассмотрим линейные уравнения с параметром вида: $$p(a)x-q(a)=0,$$ где \(p(a)\) и \(q(a)\)- выражения, которые зависят от параметра. Для того, чтобы решить такое уравнение, нужно найти все \(x\) при всех значениях параметра \(a\). Приведем наше уравнение к виду: $$p(a)x=q(a),$$ Отсюда единственное решение: \(x=\frac
Решить уравнение \(ax-5a=7x-3\) при всех возможных \(a\).
Перенесем все одночлены с \(x\) влево, а оставшиеся члены – вправо. И вынесем \(x\) за скобку, как общий множитель: $$x(a-7)=5a-3;$$ Первый случай, когда \((a-7)≠0\). Тогда мы можем поделить все уравнение на \(a-7\) и выразить: $$x=\frac<5a-3>
Ответ: При \(a=7\) \(x∈∅;\)
при \(a≠7\) \(x=\frac<5a-3>
Найдите все \(a\), при которых корнем уравнения $$ax+5a-2(3x+2)=-5x+a^2$$ будет любое число.
Раскроем скобки и перенесем все члены, содержащие \(x\), влево, а остальные – вправо. $$ax-6x+5x=-5a+4+a^2$$ Приведем подобные: $$ax-x=a^2-5a+4$$ И вынесем за скобку \(x\) и разложим квадратный многочлен на множители: $$x(a-1)=a^2-5a+4$$ $$x(a-1)=(a-1)(a-4)$$ Первый случай: \((a-1)=0\),т.е. \(a=1\) $$x*0=(a-1)(a-4)$$ $$x*0=0.$$ Решением уравнения будет любое число.
Второй случай: \((a-1)≠0\), т.е. \(a≠1\) $$x=\frac<(a-1)(a-4)>
Ответ: \(a=1.\)
Из ОДЗ видно, что \(5a+x≠0\) и \(x-5a≠0,\) таким образом, \(x≠±5a.\) Приведем уравнение к общему знаменателю \(x^2-25a^2\) и умножим на него все уравнение: $$x^2-5ax-x^2-10ax-25a^2=-100a^2$$ $$-15ax=-75a^2$$ $$ax=5a^2.$$
После преобразований получили линейное уравнение.
Первый случай: \(a=0.\) Получаем уравнение \(0*x=0.\) Решениями этого уравнения будет любое число, кроме \(x=0\) (ОДЗ \(x≠±5a\)).
Ответ: При \(a=0\) решениями уравнения будут все действительные числа, кроме \(x=0.\) Если \(a≠0,\) то решений нет.
Уравнения с параметром — алгоритмы и примеры решения
Общие сведения
Уравнением является любое математическое тождество или физический закон, в котором присутствуют неизвестные величины. Последние необходимо находить. Этот процесс называется поиском корней. Однако не во всех случаях у равенства с переменными бывают решения, а это также нужно доказать.
Корень — величина или диапазон, превращающие искомое выражение в верное равенство. Например, в 5s=10 переменная эквивалентна 2, поскольку только это значение позволяет получить верное тождество, то есть 5*2=10.
Примером диапазона или интервала решений является выражение следующего вида: 0/t=0. Его корнем может быть любое действительное число, кроме нуля. Записывается решение в таком виде: t ∈ (-inf;0)U (0;+inf), где «∈» — знак принадлежности, «-inf» и «inf» — минус и плюс бесконечно большие числа соответственно.
Параметром в уравнении называется некоторая величина, от которой зависит поведение равенства на определенном интервале. Следует отметить, что он также влияет на значение корня, когда входит с ним в различные арифметические операции: сложения, вычитания, умножения, деления, возведения в степень и так далее. Тождества такого типа называют также параметрическими. Далее необходимо разобрать классификацию уравнений.
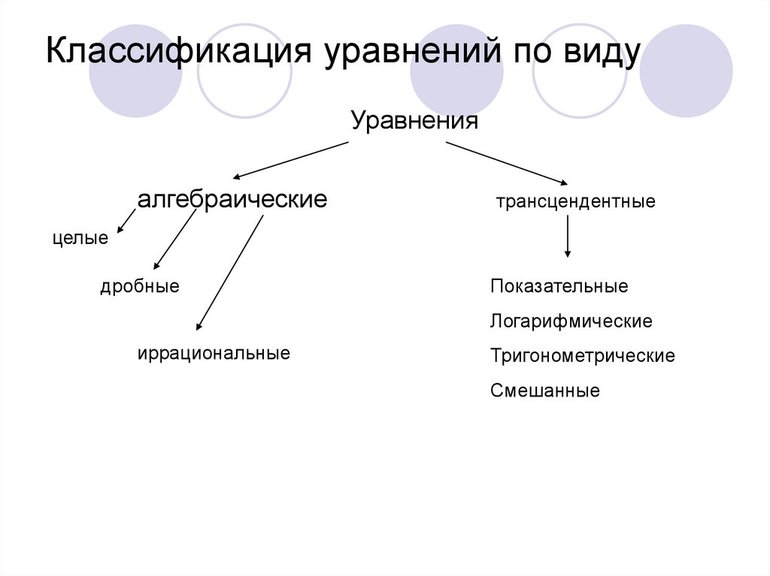
Классификация уравнений
Уравнения делятся на определенные виды, от которых зависит выбор методики их решения. Они бывают следующими: алгебраическими, дифференциальными, функциональными, трансцендентными и тригонометрическими. Кроме того, все они могут содержать некоторую величину — параметр. Его часто обозначают литерой «р» или «а».
Алгебраический тип является наиболее простым, поскольку не содержит сложные элементы. Дифференциальные тождества с неизвестными — одни из самых сложных выражений с точки зрения алгоритма. Они бывают первого, второго, третьего, а также высших порядков. Для нахождения их корней необходимо знать правила дифференцирования и интегрирования.
Практически все функциональные уравнения содержат один или более параметров. Основное их отличие от остальных заключается в функции, которая задается сложным выражением. Последнее может включать несколько неизвестных и параметрических элементов. Примером такого тождества является функция Лапласа, содержащая интеграл обыкновенного типа, а также экспоненту.
К трансцендентным относятся выражения, содержащие показательную, логарифмическую и радикальную (знак корня). Последний тип — тригонометрические. Они содержат любое равенство, содержащее следующие функции: sin, cos, tg и ctg. Однако в математике встречаются также их производные: arcsin, arccos, arcctg, arctg и гиперболические тождества.
Специалисты рекомендуют освоить на начальных этапах обучения методики, позволяющие решать уравнения с параметром линейного типа. После этого можно переходить к более сложным тождествам — функциональным, трансцендентным и так далее.
Алгебраический вид
Алгебраические не содержат в своем составе сложных функций, но в них могут присутствовать компоненты со степенным показателем.
На основании последней характеристики они делятся на 5 типов:
- Линейные.
- Квадратные (квадратичные).
- Кубические.
- Биквадратные.
- Высших порядков.
Линейные — выражения с переменной, которая имеет только первую степень (равную единице). Если показатель эквивалентен двойке, то такое тождество называется квадратным. В математической интерпретации его еще называют квадратным трехчленом. Когда показатель при неизвестной эквивалентен тройке, тогда это равенство называется кубическим.
Наиболее сложными по своей структуре являются биквадратные (содержат 4 степень). Однако на этом виды линейных уравнений не заканчиваются, поскольку бывают равенства с более высокими показателями. Их называют уравнениями высших порядков. Кроме того, любые тождества могут объединяться в системы уравнений. Их особенностью являются общие решения.
Линейные и квадратичные
Линейное — это самое простое уравнение, которое имеет всего одно решение. Оно решается по следующей методике:
- Записывается искомое выражение.
- При необходимости раскрываются скобки и приводятся подобные элементы.
- Неизвестные (переменные) остаются в левой части тождества, а все константы (числа) — переносятся вправо.
- Правая часть сокращается на коэффициент при неизвестной.
- Записывается результат.
- Выполняется проверка посредством подстановки корня в исходное выражение.
Следует отметить, что линейное выражение с переменной может не иметь решений, поскольку иногда невозможно выполнить операцию сокращения. Например, 0t=85. Равенство не имеет корней, поскольку на нулевое значение делить нельзя, так как при этом получается пустое множество.
Следующим типом является уравнение квадратичной формы At 2 +Bt+C=0. Оно может иметь один или два решения. Однако бывают случаи, при которых корней нет вообще. Для получения результата вводится понятие дискриминанта «D=(-B)^2−4*А*С». Для решения следует воспользоваться следующим алгоритмом:
- Записать выражение.
- Выполнить при необходимости математические преобразования по раскрытию скобок и приведению подобных слагаемых.
- Вычислить значение D (D 0 — два решения).
- При D=0 формула корня имеет такой вид: t=-В/(2А).
- Если D>0, то решения определяются по следующим соотношениям: t1=[-В-D^(½)]/(2А) и t2=[-В+D^(½)]/(2А).
- Записать результат.
- Выполнить проверку по отсеиванию ложных корней.
Следует отметить, что ложный корень — значение переменной, полученное по соответствующей формуле, но при подстановке в исходное выражение не выполняет условие равенства нулевому значению.
Кроме того, нужно обратить внимание на типы квадратных уравнений. Они бывают полными и неполными. Первые содержат все коэффициенты (А, В и С), а во вторых — некоторые из них могут отсутствовать, кроме А, так как тогда тождество должно содержать вторую степень при неизвестной.
Неполные решаются методом разложения на множители. Например, «v 2 −81=0» раскладывается следующим образом (формула сокращенного умножения — разность квадратов): (v-9)(t+9)=0. Анализируя последнее равенство, можно сделать вывод о понижении степени. Корнями уравнения являются два значения, t1=-9 и t2=9.
Кубичеcкие и биквадрaтные
Кубические и биквадратные равенства с неизвестным рекомендуется решать при помощи замены переменной. Однако в некоторых случаях можно применить формулы понижения степени или разложения на множители. Иными словами, суть решения алгебраических уравнений, степень которых превышает двойку, сводится к ее понижению различными методами.
Замена переменной производится на другую неизвестную величину. В примере (t 3 −2)+2t 3 −4=0 можно ввести следующий элемент — v=t 3 −2. В результате этого получится равенство такого вида: v+2v=0. Оно решается очень просто:
- Приводятся подобные элементы: 3v=0.
- Находится корень: v=0.
- Приравнивается к выражению, которое заменяли: t 3 −2=0.
- Находится корень (один, поскольку у радикала нечетная степень): t=[2]^(1/3).
- Проверяется условие: 2^(1/3)^3−2+2*(2^(1/3)^3)-4=4−4=0 (истина).
Биквадратные тождества решаются таким же методом. Однако существует еще один способ — разложение на множители. Его необходимо разобрать на примере решения выражения «4m 4 −324=0». Решать нужно по такому алгоритму:
- Упростить (вынести четверку за скобки и сократить на нее): 4 (m 4 −81)=m 4 −81=0.
- Разложить на множители (разность квадратов): (m 2 −9)(m 2 +9)=(m-3)(m+3)(m 2 +9)=0/
- Решить три уравнения: m1=3, m2=-3, m3=-3 и m4=3.
- Результат: m1=-3 и m2=3.
- Проверка: 4*(-3)^4−324=0 (истинно) и 4*(3)^4−324=0 (истинно).
Каждый из методов решения выбирается в зависимости от самого уравнения. При чтении условия задачи необходимо определить способ решения. Последний должен быть простым и удобным, а главное — количество шагов решения должно быть минимальным, что существенно сказывается на затраченном времени при вычислениях. Далее нужно рассмотреть подробный алгоритм решения уравнения с параметром.
Пример решения
На основании изученного материала можно приступить к практике решения уравнения с параметром, которое имеет следующий вид: 2v 4 −32−4p-(v 2 +4)+(v-2)(v+2)-v 4 +16=-4, где р — некоторый параметр. Корни и величину р необходимо искать по следующему алгоритму:
- Записать равенство с неизвестным и параметром: 2v 4 −32−4p-(v 2 +4)+(v-2)(v+2)-v 4 +16=-4.
- Выполнить математические преобразования: 2v 4 −32−4p-v 2 +4+v 2 −4-v 4 +16+4=v 4 −16+4p+4=0.
- Ввести замену v 4 −16=m: m+4p+4=0.
- Вывести формулу нахождения параметра: р=-(m/4)-1.
- Подставить величину m: р=-1-(v 4 +16)/4.
- C учетом соотношения равенство будет иметь такой вид: v 4 −16+4[-(v 4 +16−4)/4]+4=-32+8=0 (корней нет, поскольку -24 4 −12=0.
- Корни: v1=[12]^(¼) и v2=-[12]^(¼).
- Отрицательного корня v2 не существует, поскольку показатель радикала — четное число.
- Результат: v1=[12]^(¼).
- Проверка: <[12]^(¼)>^4−16+4=16−16=0 (истина).
Следует отметить, что v2 — ложный корень, а также параметр p, равный какому-либо значению, превращает уравнение в пустое множество. Для проверки можно воспользоваться специальным приложением, которое называется онлайн-калькулятором.
Таким образом, уравнения с параметром являются наиболее сложными, поскольку необходимо искать их корни, а также некоторое значение, влияющее на логику выражения. Для их решения необходимо следовать специальному алгоритму, предложенному математиками.
Решение линейных уравнений с параметрами
В работе показаны основные методы решения уравнений с параметрами. Материал будет полезен при подготовке к ГИА и ЕГЭ. Приведены собственные наблюдения в решении уравнений с параметрами.
Скачать:
| Вложение | Размер |
|---|---|
| В работе показаны основные методы решения линейных уравнений с параметрами. Материал будет полезен при подготовке к ЕГЭ и ГИА | 131.77 КБ |
| nauchno-issledvatelskaya_rabota.docx | 131.77 КБ |
Предварительный просмотр:
«Средняя общеобразовательная школа имени Р.З. Сагдеева»
«От гипотезы к открытию»
«Линейные уравнения и системы уравнений
Первые шаги в решении задач с параметрами
ученица 10 »А» класса Гибадуллина Камилла
учитель математики Зудина Наталия Ивановна
Г. Буинск, 2013 год
1. Виды линейных уравнений с параметрами
1.1. Линейные уравнения с параметрами и одной переменной
1.2. Линейные уравнения с параметрами и двумя переменными
2. Особенности задач с параметрами
2.1. Задачи с параметрами первого класса
2.2. Задачи с параметрами второго класса
3 Решение систем уравнений с параметрами
3.1 Методические рекомендации учащимся по выбору алгоритма решения систем линейных уравнений с параметрами
Список использованных источников
В классическом определении параметр – это некоторое фиксированное, но неизвестное число [1].
Впервые с параметрами в школьном курсе учащиеся встречаются при изучении линейных уравнений и неравенств [2].
Если в уравнении кроме неизвестных входят числа, обозначенные буквами, то они называются параметрами, а уравнение параметрическим [3].
Решить уравнение с параметром – это значит установить соответствие, с помощью которого для каждого значения параметра указывается множество корней соответствующего уравнения.
Следует отметить, что в настоящее время при изучении математики в общеобразовательных школах решению уравнений с параметрами не уделяется должного внимания. Поэтому при встрече с такого рода задачами на вступительных экзаменах в высшие учебные заведения и на олимпиадах учащимся приходится действовать на свой страх и риск, полагаясь лишь на собственное логическое мышление. Увы, правильное логическое мышление от природы не даётся, — его у себя надо развивать даже людям, способным к математике [4].
В связи с этим, целью настоящей научной работы является исследование особенностей решения линейных уравнений с параметрами и разработка методических рекомендаций учащимся по выбору алгоритма нахождения их корней.
1. Виды линейных уравнений с параметрами
1.1. Линейные уравнения с параметрами и одной переменной
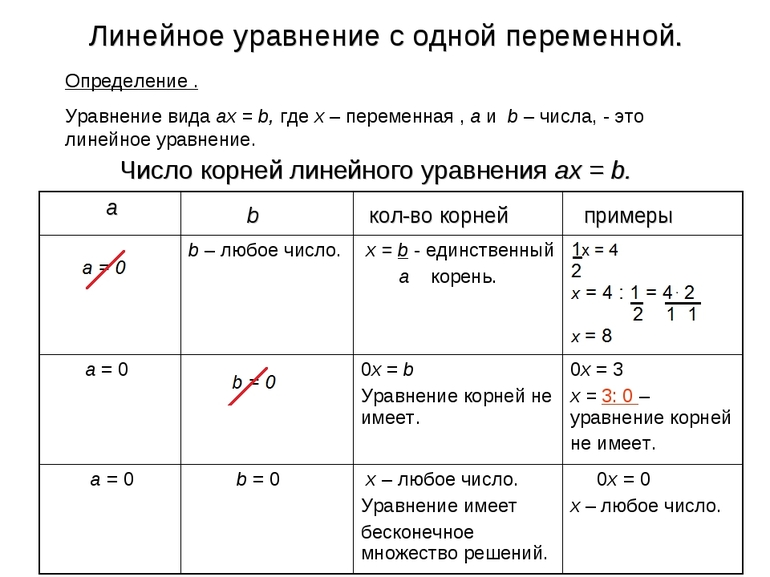
Уравнение вида a . x=b, где x- переменная, a и b – некоторые числа, называется линейным уравнением с одной переменной.
В практике решения задач с параметрами, применительно к линейным уравнениям с одной переменной, уравнения с параметрами преимущественно встречаются двух видов [5]:
— с одной переменной и одним параметром;
— с одной переменной и двумя параметрами.
К первому виду относятся уравнения, где значение одного из параметров (a или b) изначально задано условием или в уравнение входит только один параметр.
Примером могут служить уравнения вида:
Ко второму виду относятся уравнения, в которых значения параметров (a или b) изначально не определены, а обозначены буквами.
Примером могут служить уравнения вида:
1.2. Линейные уравнения с параметрами и двумя
Уравнение вида a . x+b . y=c, где x и y — переменные, a, b и c – некоторые числа, называется линейным уравнением с двумя переменными.
В практике решения задач с параметрами, применительно к линейным уравнениям с двумя переменным, и уравнения с параметрами преимущественно встречаются двух видов [5]:
— с двумя переменными и одним параметром;
— с двумя переменными и двумя параметрами.
К первому виду относятся уравнения, где значение двух из трех параметров (a, b или c) изначально заданы условием или в уравнение входит только один параметр.
Примером могут служить уравнения вида:
Ко второму виду относятся уравнения, где значение одного из трех параметров (a, b или c) изначально задано условием, а значения остальных двух параметров не определены, а обозначены буквами.
Примером могут служить уравнения вида:
Следует отметить, что на данном этапе особенности решения линейных уравнений с параметрами и двумя переменными не являлись предметом исследований, поэтому их классификация приведена лишь в ознакомительном плане.
2. Особенности задач с параметрами
Все задачи с параметрами можно условно разбить на два класса [6].
К первому классу относятся задачи, в которых требуется решить уравнение при всех значениях параметра.
Ко второму классу – задачи, в которых нужно из всех значений параметра выделить те, при которых уравнение будет обладать некоторыми задаваемыми свойствами, например, будет выполняться при любом значении переменной, или вообще не будет иметь решений, или будет иметь только одно положительное или отрицательное решение и т. д.
2.1. Задачи с параметрами первого класса
В задачах первого класса нужно провести полное исследование решения, которое заключается, как правило, в обязательном рассмотрении следующих случаев решения уравнения[7]:
— случай, при котором уравнение не имеет смысла;
— случай, при котором уравнение не имеет решения;
— случай, при котором уравнение имеет единственное решение или конечное число конкретных решений;
— случай, при котором уравнение имеет бесчисленное множество решений.
Ответ в задачах первого класса обычно формулируется следующим образом:
Ответ: уравнение при таких – то значениях параметров имеет корни…, при таких – то значениях параметров – бесчисленное множество решений, решением уравнения является любое действительное число, при таких – то значениях параметров уравнение корней не имеет, при таких – то значениях параметров не имеет смысла.
Особенностью решения линейных параметрических уравнений данного класса является рассмотрение двух случаев:
а) коэффициент при переменной равен нулю;
в) коэффициент при переменной не равен нулю.
В качестве примера рассмотрим решение уравнения с одной переменной и одним параметром:
Решение уравнения сводится к рассмотрению двух случаев.
1) Если коэффициент при х равен нулю, т.е. а-1=0, а=1, то получим уравнение 0 . х=1, которое не имеет решений.
Ответ: при а=1 — нет корней; при а≠1, х = .
В данном уравнении значение параметра – а, равное единице, обращает коэффициент (а-1) при переменной х в нуль.
В задачах с параметрами принято значение параметра, обращающего коэффициент при неизвестном (переменной) в нуль называть контрольным .
Так, например в уравнении:
значение параметра – а. равное -6, является контрольным, так как обращает коэффициент (а+6) при неизвестном – х в нуль.
Решение уравнения сводится к рассмотрению двух случаев.
Если m=0, уравнение имеет вид 0·x=1, которое не имеет корней.
Если m≠0, то можно разделить обе части уравнения на m, и уравнение имеет единственное решение x = .
Ответ: при m=0 уравнение не имеет решений, при m≠0 уравнение имеет единственное решение x =
Решение уравнения сводится к двум случаям.
Если коэффициент при x равен нулю, т. е. n−1=0, n=1, то получим уравнение 0·x=1, которое не имеет решений.
Если n≠1, то уравнение имеет единственное решение x =
Ответ: при n=1 не имеет решений, при n≠1 уравнение имеет единственное решение x =
Решение уравнения сводится к рассмотрению двух случаев.
Определим контрольное значение параметра b, для чего приравняем коэффициент при неизвестном к нулю, т. е.b+3=0, b=−3 — контрольное значение. Исследуем и решим уравнение относительно найденного контрольного значения параметра.
Если b=−3, то получим уравнение 0·x=0, которое имеет бесчисленное множество решений.
Если b≠−3,то x = уравнение имеет единственное решение x=1.
Ответ: при b=−3 уравнение имеет бесчисленное множество решений, x-любое действительное число , при b≠3 x=1.
2.2. Задачи с параметрами второго класса.
В задачах второго класса не следует проводить полного исследования решения задачи, а достаточно привести решение, которое приведет к ответу на поставленный вопрос задачи[7].
Вопрос в задачах второго класса формулируется, как правило, следующим образом:
Вопрос: При каком значении параметра уравнение…:
-не имеет смысла;
— не имеет решения;
— имеет единственное решение или конечное число конкретных решений;
— имеет бесчисленное множество решений и т.п.?
В качестве примера рассмотрим решение уравнения:
с вопросом задачи: При каком значении параметра — а уравнение не имеет корней?
Решение: При значении параметра – а, равном единице, знаменатель дроби уравнения обращается в нуль, поэтому уравнение не имеет смысла.
Ответ: при а=1 уравнение теряет смысл и не имеет корней.
В задачах с параметрами принято значение параметра, при котором уравнение имеет смысл называть допустимым .
В рассмотренном примере допустимыми значениями параметра – а являются все действительные числа кроме единицы.
При каком значении параметра а корнем уравнения ax−100x=a−100 является любое число?
Преобразуем данное уравнение к виду (a−100)x=a−100, используя распределительное свойство умножения
Определим контрольное значение параметра: a−100=0, a=100При a=100 уравнение имеет вид 0·x=0, решением которого является любое действительное число.
Ответ: при a=100 x-любое число.
При каком значении параметра s уравнение (3−2s)x=0 имеет единственное решение?
Определим контрольное значение параметра: 3−2s=0, s=1,5
При s≠1,5 уравнение имеет один корень x =0
Ответ: при s≠1,5, уравнение имеет единственное решение.
При каком значении параметра k, уравнение 2·x = не имеет корней?
При k=−3 знаменатель дроби уравнения обращается в нуль, поэтому уравнение не имеет смысла.
Ответ: при k=−3 уравнение теряет смысл.
3.Методы решения систем линейных уравнений
Определение: Система вида
где A 1, A 2, B 1 ,B 2, C 1 C 2 – выражения , зависящие от параметров, а х и у – неизвестные, называется системой двух линейных алгебраических уравнений с двумя неизвестными в параметрах. Возможны следующие случаи:
1) Если , то система имеет единственное решение
2) Если , то система не имеет решений
3) Если , то система имеет бесконечно много решений.
Пример 1. При каких значениях параметра а система
- 2х — 3у = 7
- ах — 6у = 14
- а) имеет бесконечное множество решений;
б) имеет единственное решение
а) если а=4, то система имеет бесконечное множество решений;
б) если а 4, то решение единственное.
Решите систему уравнений
Решение: а) , т.е. при m 1 система имеет единственное решение.
б) , т.е. при m=1 (2=m+1) и n 1 исходная система решений не имеет
в) , при m=1 и n=1 система имеет бесконечно много решений.
Ответ: а) если m=1 и n 1, то решений нет
б) m=1 и n=1, то решение бесконечное множество
в) если m 1 и n — любое, то
Рассмотрим II способ решения системы (1).
Решим систему (1) методом алгебраического сложения: вначале умножим первое уравнение системы на В 2, второе на – В 1 и сложим почленно эти уравнения, исключив, таким образом, переменную у:
Т.к. А 1 В 2 -А 2 В 1 0, то х =
Теперь исключим переменную х. Для этого умножим первое уравнение системы (1) на А 2 , а второе на – А 1 , и оба уравнения сложим почленно:
- А 1 А 2 х +А 2 В 1 у=А 2 С 1
- -А 1 А 2 х-А 1 В 2 у=-А 1 С 2
- у(А 2 В 1 -А 1 В 2 )=А 2 С 1 -А 1 С 2
т.к. А 2 В 1 -А 1 В 2 0 у =
Для удобства решения системы (1) введем обозначения:
Теперь решение системы (1) можно записать с помощью определителей:
Приведенные формулы называют формулами Крамера.
— Если , то система (1) имеет единственное решение: х= ; у=
— Если , или , , то система (1) не имеет решений
— Если , , , , то система (1) имеет бесконечное множество решений.
В этом случае систему надо исследовать дополнительно. При этом, как правило, она сводится к одному линейному уравнению. В случае часто бывает удобно исследовать систему следующим образом: решая уравнение , найдем конкретные значения параметров или выразим один из параметров через остальные и подставим эти значения параметров в систему. Тогда получим систему с конкретными числовыми коэффициентами или с меньшим числом параметров, которую надо и исследовать.
Если коэффициенты А 1 , А 2 , В 1 , В 2 , системы зависят от нескольких параметров, то исследовать систему удобно с помощью определителей системы.
Пример 3.Для всех значений параметра а решить систему уравнений
Решение: Найдем определитель системы:
= (а+5)(5а+6) – (3а+10) (2а+3)= 5а 2 +31а+30-6а 2 -29а-30=-а 2 +2а=а(2-а)
= (3а+2) (5а+6) –(2а+4)(2а+3)=15а 2 +28а+12-4а 2 -14а-12=11а 2 +14а=а(11а+14)
=(а+5) (2а+4)-(3а+10)(3а+2)=2а 2 +14а+20-9а 2 -36а-20=-7а 2 -22а=-а(7а+22)
При а=0 определители
Тогда система имеет вид:
При а=2 Этого достаточно, чтобы утверждать, что система не имеет решений.
Ответ:1) если а и а , то х= у=
3) если а=2, то (х; у)
3.1 Методические рекомендации учащимся по выбору
алгоритма решения линейных уравнений с параметрами
Рассмотрим решение вышеприведенных линейных уравнений с параметрами в общемвиде .Исследуем, сколько корней может иметь линейное уравнение с одним неизвестным ax = b.
1.Если a ≠0, b – любое число то уравнение имеет один корень x =
Определим знак корня
— корень положительный( x>0 ), если а и b – одинакового знака, т.е. a>0, b>0 или a
В более сложных или общих случаях, в том числе при решении линейных уравнений с одной неизвестной и двумя параметрами удобнее пользоваться алгоритмом, блок-схема которого приведена на рис
http://nauka.club/matematika/algebra/uravneniya-s-parametrom.html
http://nsportal.ru/ap/library/nauchno-tekhnicheskoe-tvorchestvo/2014/05/10/reshenie-lineynykh-uravneniy-s-parametrami