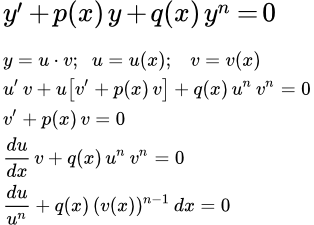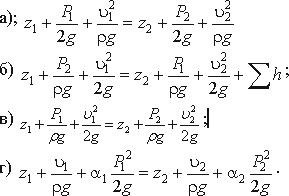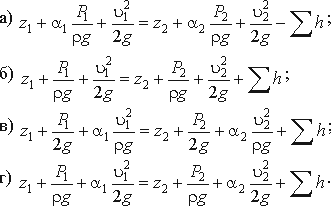Виды уравнений бернулли в тестах

Дифференциальное уравнение Бернулли и методы его решения

Решение дифференциального уравнения Бернулли приведением к линейному уравнению

Рассмотрим дифференциальное уравнение Бернулли:
(1) ,
где n ≠ 0 , n ≠ 1 , p и q – функции от x .
Разделим его на y n . При y ≠ 0 или n 0 имеем:
(2) .
Это уравнение сводится к линейному с помощью замены переменной:
.
Покажем это. По правилу дифференцирования сложной функции:
;
.
Подставим в (2) и преобразуем:
;
.
Это – линейное, относительно z , дифференциальное уравнение. После его решения, при n > 0 , следует рассмотреть случай y = 0 . При n > 0 , y = 0 также является решением уравнения (1) и должно входить в ответ.

Решение методом Бернулли

Рассматриваемое уравнение (1) также можно решить методом Бернулли. Для этого ищем решение исходного уравнения в виде произведения двух функций:
y = u·v ,
где u и v – функции от x . Дифференцируем по x :
y′ = u′ v + u v′ .
Подставляем в исходное уравнение (1):
;
(3) .
В качестве v возьмем любое, отличное от нуля, решение уравнения:
(4) .
Уравнение (4) – это уравнение с разделяющимися переменными. Решаем его и находим частное решение v = v ( x ) . Подставляем частное решение в (3). Поскольку оно удовлетворяет уравнению (4), то выражение в круглых скобках обращается в нуль. Получаем:
;
.
Здесь v – уже известная функция от x . Это уравнение с разделяющимися переменными. Находим его общее решение, а вместе с ним и решение исходного уравнения y = uv .

Примеры решений дифференциального уравнения Бернулли

Пример 1

Решить уравнение
(П1.1)

Это дифференциальное уравнение Бернулли. Решаем его методом Бернулли. Ищем решение в виде произведения двух функций: . Тогда
. Подставляем в (П1.1):
;
(П1.2) .
Одну из этих функций мы можем выбрать произвольным образом. Выберем v так, чтобы выражение в круглых скобках равнялось нулю:
(П1.3) .
Тогда подставляя (П1.3) в (П1.2), мы получим дифференциальное уравнение с разделяющимися переменными:
(П1.4) .

Сначала мы определим функцию v . Нам нужно найти любое, отличное от нуля, решение уравнения (П1.3). Решаем его. Для этого разделяем переменные и интегрируем.
;
;
;
;
.
Отсюда , или . Возьмем решение с и знаком ′плюс′. Тогда , или .

Итак, мы нашли функции u и v . Находим искомую функцию y :
.
Заменим постоянную интегрирования: . Тогда общее решение исходного уравнения (П1.1) примет вид:
.

Когда мы делили на u , то предполагали, что . Теперь рассмотрим случай . Тогда . Нетрудно видеть, что постоянная функция также является решением исходного уравнения (П1.1) ⇑.

Общее решение уравнения: .
Уравнение также имеет решение .

Пример 2

На первый взгляд, кажется, что это дифференциальное уравнение не похоже на уравнение Бернулли. Если считать x независимой переменной, а y – зависимой (то есть если y – это функция от x ), то это так. Но если считать y независимой переменной, а x – зависимой, то легко увидеть, что это – уравнение Бернулли.

Итак, считаем что x является функцией от y . Подставим в исходное уравнение и умножим на :
;
;
(П2.1) .
Это – уравнение Бернулли с n = 2 . Оно отличается от рассмотренного выше, уравнения (1), только обозначением переменных ( x вместо y ). Решаем методом Бернулли. Делаем подстановку:
x = u v ,
где u и v – функции от y . Дифференцируем по y :
.
Подставим в (П2.1):
;
(П2.2) .
Ищем любую, отличную от нуля функцию v ( y ) , удовлетворяющую уравнению:
(П2.3) .
Разделяем переменные и интегрируем:
;
;
.
Поскольку нам нужно любое решение уравнения (П2.3), то положим C = 0 :
; ; .
Возьмем решение со знаком ′плюс′:
.
Подставим в (П2.2) учитывая, что выражение в скобках равно нулю (ввиду (П2.3)):
;
;
.
Разделяем переменные и интегрируем. При u ≠ 0 имеем:
;
(П2.4) ;
.
Во втором интеграле делаем подстановку :
;
.
Интегрируем по частям:
;
.
Подставляем в (П2.4):
.
Возвращаемся к переменной x :
;
;
.

Автор: Олег Одинцов . Опубликовано: 07-08-2012 Изменено: 29-10-2020

Дифференциальные уравнения Бернулли в примерах решений

Дифференциальным уравнением Бернулли называется уравнение вида

,

Таким образом, дифференциальное уравнение Бернулли обязательно содержит функцию y в степени, отличной от нуля и единицы.

В случае, если m = 0 , уравнение является линейным, а в случае, если m = 1 , уравнение является уравнением с разделяющимися переменными.

Дифференциальное уравнение Бернулли можно решить двумя методами.

1. Переходом с помощью подстановки к линейному уравнению.
2. Методом Бернулли.

Переход от уравнения Бернулли к линейному уравнению.

Уравнение делим на :

,

.

Обозначим . Тогда , откуда . Переходя к новой переменной, получим уравнение

,

которое является линейным дифференциальным уравнение первого порядка. Его можно решить методом вариации константы Лагранжа или методом Бернулли.

Решение методом Бернулли.

Решение следует искать в виде произведения двух функций y = u ⋅ v . Подставив его в дифференциальное уравнение, получим уравнение

.

Из слагаемых, содержащих функцию u в первой степени, вынесем её за скобки:

.

Приравняв выражение в скобках нулю, то есть

,

получим дифференциальное уравнение с разделяющимися переменными для определения функции v .

Функцию u следует находить из дифференциального уравнения

,

которое также является уравнение с разделяющимися переменными.

Пример 1. Решить дифференциальное уравнение Бернулли

.

Решение. Решим дифференциальное уравнение двумя методами.

1. Переход от уравнения Бернулли к линейному уравнению. Данное уравнение умножим на y³ :

.

Введём обозначение , тогда , и приходим к уравнению

.

Решим его методом Бернулли. В последнее уравнение подставим z = u ⋅ v , z‘ = u‘v + uv‘ :

,

.

Выражение в скобках приравняем нулю и решим полученное дифференциальное уравнение:

Полученную функцию v подставим в уравнение:

2. Методом Бернулли. Ищем решение в виде произведения двух функций y = u ⋅ v . Подставив его и y‘ = u‘v + uv‘ в данное дифференциальное уравнение, получим

Выражение в скобках приравняем нулю и определим функцию v :

Полученную функцию v подставим в уравнение и определим функцию u :

И, наконец, найдём решение данного дифференциального уравнения:

Пример 2. Решить дифференциальное уравнение Бернулли

.

Решение. Это уравнение, в котором m = −1 . Применив подстановку y = u ⋅ v , получим

Выражение в скобках приравняем нулю и определим функцию v :

Полученную функцию v подставим в уравнение и определим функцию u :

Таким образом, получаем решение данного дифференциального уравнения:

.

Пример 3. Решить дифференциальное уравнение Бернулли

.

Решение. Это уравнение можно решить, используя подстановку y = u ⋅ v . Получаем

Приравняем нулю выражение в скобках и решим полученное уравнение с разделяющимися переменными:

Подставляем v в данное уравнение и решаем полученное уравнение:

и проинтегрируем обе части уравнения:

Далее используем подстановку

:

.

Таким образом, получаем функцию u :

.

и решение данного дифференциального уравнения:

Пример 4. Решить задачу Коши для дифференциального уравнения

при условии .

Решение. Перепишем уравнение, перенося в левую сторону линейные слагаемые, а в правую — нелинейные:

.

Это уравнение Бернулли, которое можно решить, используя подстановку y = u ⋅ v , y‘ = u‘v + uv‘ :

Выражение в скобках приравняем нулю и решим дифференциальное уравнение с разделяющимися переменными:

Подставим функцию v в данное уравнение и решим полученное дифференциальное уравнение:

Вычислим каждый интеграл отдельно. Первый:

.

Второй интеграл интегрируем по частям. Введём обозначения:

Приравниваем друг другу найденные значения интегралов и находим функцию u :

Таким образом, общее решение данного дифференциального уравнения:

.

Используем начальное условие, чтобы определить значение константы:

Ищем частное решение, удовлетворяющее начальному условию:

В результате получаем следующее частное решение данного дифференциального уравнения:

.

И напоследок — пример с альтернативным обозначением производных — через дробь.

Пример 5. Решить дифференциальное уравнение Бернулли

.

Решение. Решим это уравнение первым из представленных в теоретической части методом — переходом к линейному уравнению. Разделив данное уравнение почленно на y³ , получим

.

Введём новую функцию . Тогда

.

Подставляя эти значения в уравнение, полученное на первом шаге, получим линейное уравнение:

.

Найдём его общий интеграл:

,

.

Подставляя эти значение в полученное линейное уравнение, получаем

.

Приравниваем нулю выражение в скобках:

Для определения функции u получаем уравнение

.

Интегрируем по частям:

Таким образом, общий интеграл данного уравнения

.

Виды уравнений бернулли в тестах

3.1. Площадь поперечного сечения потока, перпендикулярная направлению движения называется

а) открытым сечением;
б) живым сечением;
в) полным сечением;
г) площадь расхода.

3.2. Часть периметра живого сечения, ограниченная твердыми стенками называется

а) мокрый периметр;
б) периметр контакта;
в) смоченный периметр;
г) гидравлический периметр.

3.3. Объем жидкости, протекающий за единицу времени через живое сечение называется

а) расход потока;
б) объемный поток;
в) скорость потока;
г) скорость расхода.

3.4. Отношение расхода жидкости к площади живого сечения называется

а) средний расход потока жидкости;
б) средняя скорость потока;
в) максимальная скорость потока;
г) минимальный расход потока.

3.5. Отношение живого сечения к смоченному периметру называется

а) гидравлическая скорость потока;
б) гидродинамический расход потока;
в) расход потока;
г) гидравлический радиус потока.

3.6. Если при движении жидкости в данной точке русла давление и скорость не изменяются, то такое движение называется

а) установившемся;
б) неустановившемся;
в) турбулентным установившимся;
г) ламинарным неустановившемся.

3.7. Движение, при котором скорость и давление изменяются не только от координат пространства, но и от времени называется

а) ламинарным;
б) стационарным;
в) неустановившимся;
г) турбулентным.

3.8. Расход потока обозначается латинской буквой

3.9. Средняя скорость потока обозначается буквой

3.10. Живое сечение обозначается буквой

3.11. При неустановившемся движении, кривая, в каждой точке которой вектора скорости в данный момент времени направлены по касательной называется

а) траектория тока;
б) трубка тока;
в) струйка тока;
г) линия тока.

3.12. Трубчатая поверхность, образуемая линиями тока с бесконечно малым поперечным сечением называется

а) трубка тока;
б) трубка потока;
в) линия тока;
г) элементарная струйка.

3.13. Элементарная струйка — это

а) трубка потока, окруженная линиями тока;
б) часть потока, заключенная внутри трубки тока;
в) объем потока, движущийся вдоль линии тока;
г) неразрывный поток с произвольной траекторией.

3.14. Течение жидкости со свободной поверхностью называется

а) установившееся;
б) напорное;
в) безнапорное;
г) свободное.

3.15. Течение жидкости без свободной поверхности в трубопроводах с повышенным или пониженным давлением называется

а) безнапорное;
б) напорное;
в) неустановившееся;
г) несвободное (закрытое).

3.16. Уравнение неразрывности течений имеет вид

3.17. Уравнение Бернулли для идеальной жидкости имеет вид

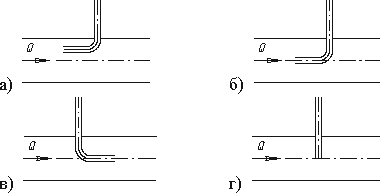
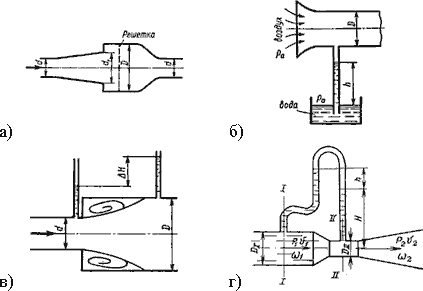
3.18. На каком рисунке трубка Пито установлена правильно

3.19. Уравнение Бернулли для реальной жидкости имеет вид

3.20. Член уравнения Бернулли, обозначаемый буквой z, называется

а) геометрической высотой;
б) пьезометрической высотой;
в) скоростной высотой;
г) потерянной высотой.

3.21. Член уравнения Бернулли, обозначаемый выражением 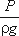называется

а) скоростной высотой;
б) геометрической высотой;
в) пьезометрической высотой;
г) потерянной высотой.

3.22. Член уравнения Бернулли, обозначаемый выражением 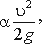называется

а) пьезометрической высотой;
б) скоростной высотой;
в) геометрической высотой;
г) такого члена не существует.

3.23. Уравнение Бернулли для двух различных сечений потока дает взаимосвязь между

а) давлением, расходом и скоростью;
б) скоростью, давлением и коэффициентом Кориолиса;
в) давлением, скоростью и геометрической высотой;
г) геометрической высотой, скоростью, расходом.

3.24. Коэффициент Кориолиса в уравнении Бернулли характеризует

а) режим течения жидкости;
б) степень гидравлического сопротивления трубопровода;
в) изменение скоростного напора;
г) степень уменьшения уровня полной энергии.

3.25. Показание уровня жидкости в трубке Пито отражает

а) разность между уровнем полной и пьезометрической энергией;
б) изменение пьезометрической энергии;
в) скоростную энергию;
г) уровень полной энергии.

3.26. Потерянная высота характеризует

а) степень изменения давления;
б) степень сопротивления трубопровода;
в) направление течения жидкости в трубопроводе;
г) степень изменения скорости жидкости.

3.27. Линейные потери вызваны

а) силой трения между слоями жидкости;
б) местными сопротивлениями;
в) длиной трубопровода;
г) вязкостью жидкости.

3.28. Местные потери энергии вызваны

а) наличием линейных сопротивлений;
б) наличием местных сопротивлений;
в) массой движущейся жидкости;
г) инерцией движущейся жидкоcти.

3.29. На участке трубопровода между двумя его сечениями, для которых записано уравнение Бернулли можно установить следующие гидроэлементы

а) фильтр, отвод, гидромотор, диффузор;
б) кран, конфузор, дроссель, насос;
в) фильтр, кран, диффузор, колено;
г) гидроцилиндр, дроссель, клапан, сопло.

3.30. Укажите правильную запись

3.31. Для измерения скорости потока используется

а) трубка Пито;
б) пьезометр;
в) вискозиметр;
г) трубка Вентури.

3.32. Для измерения расхода жидкости используется

а) трубка Пито;
б) расходомер Пито;
в) расходомер Вентури;
г) пьезометр.

3.33. Укажите, на каком рисунке изображен расходомер Вентури

3.34. Установившееся движение характеризуется уравнениями

3.35. Расход потока измеряется в следующих единицах

3.36. Для двух сечений трубопровода известны величины P₁, υ₁, z₁ и z₂. Можно ли определить давление P₂ и скорость потока υ₂?

а) можно;
б) можно, если известны диаметры d₁ и d₂;
в) можно, если известен диаметр трубопровода d₁;
г) нельзя.

3.37. Неустановившееся движение жидкости характеризуется уравнением

3.38. Значение коэффициента Кориолиса для ламинарного режима движения жидкости равно

3.39. Значение коэффициента Кориолиса для турбулентного режима движения жидкости равно

3.40. По мере движения жидкости от одного сечения к другому потерянный напор

а) увеличивается;
б) уменьшается;
в) остается постоянным;
г) увеличивается при наличии местных сопротивлений.

3.41. Уровень жидкости в трубке Пито поднялся на высоту H = 15 см. Чему равна скорость жидкости в трубопроводе