Виды уравнения и неравенства с параметрами

Учебное пособие «Уравнения и неравенства с параметрами»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Государственное бюджетное общеобразовательное учреждение

Самарской области средняя общеобразовательная

школа № 2 им. В. Маскина ж.-д. ст. Клявлино

муниципального района Клявлинский

« Уравнения и неравенства с параметрами» для учащихся 10 –11 классов

данное пособие является приложением к программе элективного курса «Уравнения и неравенства с параметрами», которая прошла внешнюю экспертизу (научно-методическим экспертным советом министерства образования и науки Самарской области от 19 декабря 2008 года бала рекомендована к использованию в образовательных учреждениях Самарской области)

Авторы

учитель математики МОУ Клявлинской средней общеобразовательной

школы № 2 им. В.Маскина Клявлинского района Самарской области

Ромаданова Ирина Владимировна

учитель математики МОУ Клявлинской средней общеобразовательной

школы № 2 им. В.Маскина Клявлинского района Самарской области

Сербаева Ирина Алексеевна

Линейные уравнения и неравенства с параметрами……………..4-7

Квадратные уравнения и неравенства с параметрами……………7-9

Дробно- рациональные уравнения с параметрами……………..10-11

Иррациональные уравнения и неравенства с параметрами……11-13

Тригонометрические уравнения и неравенства с параметрами.14-15

Показательные уравнения и неравенства с параметрами………16-17

Логарифмические уравнения и неравенства с параметрами…. 16-18

Задания для самостоятельной работы…………………………. 21-28

Уравнения и неравенства с параметрами.

Если в уравнении или неравенстве некоторые коэффициенты заданы не конкретными числовыми значениями, а обозначены буквами, то они называются параметрами, а само уравнение или неравенство параметрическим.

Для того, чтобы решить уравнение или неравенство с параметрами необходимо:

Выделить особое значение — это то значение параметра, в котором или при переходе через которое меняется решение уравнения или неравенства.

Определить допустимые значения – это значения параметра, при которых уравнение или неравенство имеет смысл.

Решить уравнение или неравенство с параметрами означает:

1) определить, при каких значениях параметров существуют решения;

2) для каждой допустимой системы значений параметров найти соответствующее множество решений.

Решить уравнение с параметром можно следующими методами: аналитическим или графическим.

Аналитический метод предполагает задачу исследования уравнения рассмотрением нескольких случаев, ни один из которых нельзя упустить.

Решение уравнения и неравенства с параметрами каждого вида аналитическим методом предполагает подробный анализ ситуации и последовательное исследование, в ходе которого возникает необходимость «аккуратного обращения» с параметром.

Графический метод предполагает построение графика уравнения, по которому можно определить, как влияет соответственно, на решение уравнения изменение параметра. График подчас позволяет аналитически сформулировать необходимые и достаточные условия для решения поставленной задач. Графический метод решения особенно эффективен тогда, когда нужно установить, сколько корней имеет уравнение в зависимости от параметра и обладает несомненным преимуществом увидеть это наглядно.

§ 1. Линейные уравнения и неравенства.

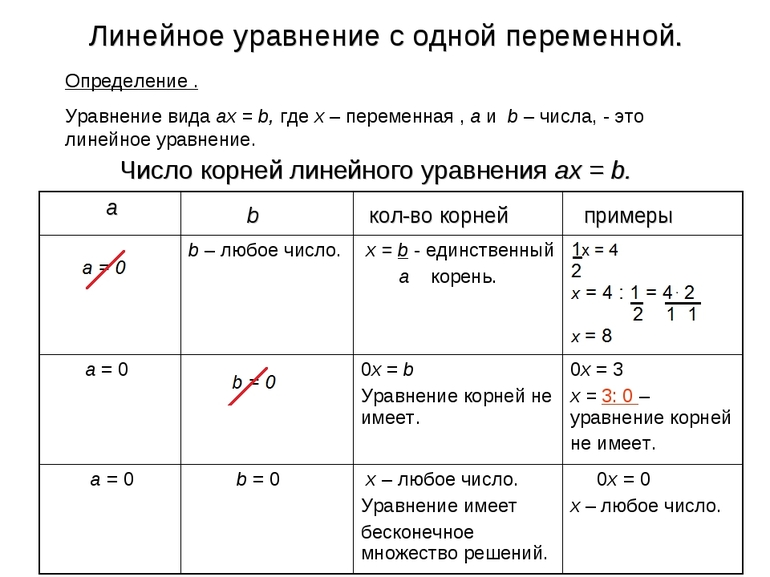
Линейное уравнение а x = b , записанное в общем виде, можно рассматривать как уравнение с параметрами, где x – неизвестное, a , b – параметры. Для этого уравнения особым или контрольным значением параметра является то, при котором обращается в нуль коэффициент при неизвестном.

При решении линейного уравнения с параметром рассматриваются случаи, когда параметр равен своему особому значению и отличен от него.

Особым значением параметра a является значение а = 0.

Если а ¹ 0, то при любой паре параметров а и b оно имеет единственное решение х=.

Если а = 0, то уравнение принимает вид : 0х= b . В этом случае значение

b = 0 является особым значением параметра b .

При b ¹ 0 уравнение решений не имеет.

При b = 0 уравнение примет вид: 0х = 0. Решением данного уравнения является любое действительное число.

Неравенства вида ах > b и ax b ( а ≠ 0) называются линейными неравенствами. Множество решений неравенства ах > b – промежуток

(; +), если a > 0 , и (-;) , если а . Аналогично для неравенства

ах b множество решений – промежуток (-;), если a > 0, и (; +), если а

Пример 1. Решить уравнение ах = 5

Решение : Это линейное уравнение .

Если а = 0, то уравнение 0 × х = 5 решения не имеет.

Если а ¹ 0, х = — решение уравнения.

Ответ: при а ¹ 0, х=

при а = 0 решения нет.

Пример 2. Решить уравнение ах – 6 = 2а – 3х.

Решение: Это линейное уравнение, ах – 6 = 2а – 3х (1)

ах + 3х = 2а +6

Переписав уравнение в виде (а+3)х = 2(а+3), рассмотрим два случая:

Если а= -3, то любое действительное число х является корнем уравнения (1). Если же а ¹ -3, уравнение (1) имеет единственный корень х = 2.

Ответ: При а = -3, х R ; при а ¹ -3, х = 2.

Пример 3. При каких значениях параметра а среди корней уравнения

2ах – 4х – а 2 + 4а – 4 = 0 есть корни больше 1 ?

Решение: Решим уравнение 2ах – 4х – а 2 + 4а – 4 = 0 – линейное уравнение

2(а — 2) х = а 2 – 4а +4

2(а — 2) х = (а – 2) 2

При а = 2 решением уравнения 0х = 0 будет любое число, в том числе и большее 1.

При а ¹ 2 х =. По условию х > 1, то есть >1, а > 4.

Ответ: При а <2>U (4;∞).

Пример 4. Для каждого значения параметра а найти количество корней уравнения ах=8.

Решение. ах = 8 – линейное уравнение.

а =,

y = a – семейство горизонтальных прямых;

y = — графиком является гипербола. Построим графики этих функций.

Ответ: Если а =0, то уравнение решений не имеет. Если а ≠ 0, то уравнение имеет одно решение.

Пример 5. С помощью графиков выяснить, сколько корней имеет уравнение:

y = ах – 1 – графиком является прямая, проходящая через точку (0;-1).

Построим графики этих функций.

Ответ:При|а|>1— один корень

при | а|≤1 – уравнение корней не имеет.

Решение : ах + 4 > 2х + а 2 (а – 2) х > а 2 – 4. Рассмотрим три случая.

а=2 . Неравенство 0 х > 0 решений не имеет.

а > 2. (а – 2) х > ( а – 2)(а + 2) х > а + 2

а (а – 2) х > ( а – 2)(а + 2) х а + 2

Ответ. х > а + 2 при а > 2; х при а при а=2 решений нет.

§ 2. Квадратные уравнения и неравенства

Для решения квадратных уравнений с параметром можно использовать стандартные способы решения на применение следующих формул:

1 ) дискриминанта квадратного уравнения: D = b ² — 4 ac , (²- ас)

2) формул корней квадратного уравнения: х 1 =, х 2 =,

(х 1,2 = )

Квадратными называются неравенства вида

Множество решений неравенства (3) получается объединением множеств решений неравенства (1) и уравнения , a х 2 + b х + с=0. Аналогично находится множество решений неравенства (4).

Если дискриминант квадратного трехчлена a х 2 + b х + с меньше нуля, то при а >0 трехчлен положителен при всех х R .

Если квадратный трехчлен имеет корни (х 1 2 ), то при а > 0 он положителен на множестве (-; х 2 )( х 2; +) и отрицателен на интервале

(х 1 ; х 2 ). Если а 1 ; х 2 ) и отрицателен при всех х (-; х 1 )( х 2; +).

Пример 1. Решить уравнение ах² — 2 (а – 1)х – 4 = 0.

Это квадратное уравнение

Решение: Особое значение а = 0.

При а = 0 получим линейное уравнение 2х – 4 = 0. Оно имеет единственный корень х = 2.

При а ≠ 0. Найдем дискриминант.

Если а = -1, то D = 0 – один корень.

Найдем корень, подставив вместо а = -1.

-х² + 4х – 4= 0, то есть х² -4х + 4 = 0, находим, что х=2.

Если а ≠ — 1 , то D >0 . По формуле корней получим: х=;

х 1 =2, х 2 = —.

Ответ: При а=0 и а= -1 уравнение имеет один корень х = 2; при а ≠ 0 и

а ≠ — 1 уравнение имеет два корня х 1 =2, х 2 =-.

Пример 2. Найдите количество корней данного уравнения х²-2х-8-а=0 в зависимости от значений параметра а.

Решение. Перепишем данное уравнение в виде х²-2х-8=а

y = х²-2х-8— графиком является парабола;

y =а— семейство горизонтальных прямых.

Построим графики функций.

Ответ: При а -9, уравнение имеет два решения.

Пример 3. При каких а неравенство (а – 3) х 2 – 2ах + 3а – 6 >0 выполняется для всех значений х ?

Решение. Квадратный трехчлен положителен при всех значениях х, если

, откуда следует, что a > 6 .

§ 3. Дробно- рациональные уравнения с параметром,

сводящиеся к линейным

Процесс решения дробных уравнений выполняется по обычной схеме: дробное заменяется целым путем умножения обеих частей уравнения на общий знаменатель левой и правой его частей. После чего решается целое уравнение, исключая посторонние корни, то есть числа, которые обращают знаменатель в нуль.

В случае уравнений с параметром эта задача более сложная. Здесь, чтобы «исключить» посторонние корни, требуется найти значение параметра, обращающее общий знаменатель в нуль, то есть решить соответствующие уравнения относительно параметра.

Пример 1. Решить уравнение = 0

Это дробно- рациональное уравнение

Решение: Д.З: х +2 ≠ 0 , х ≠ -2

При а = -2 корней нет.

Пример 2 . Решить уравнение— = (1)

Это дробно- рациональное уравнение

Решение: Значение а = 0 является особым. При а = 0 уравнение теряет смысл и, следовательно, не имеет корней. Если а ≠ 0, то после преобразований уравнение примет вид: х² + 2 (1-а) х + а² — 2а – 3 = 0 (2) – квадратное уравнение.

Найдем дискриминант = (1 – а)² — (а² — 2а – 3)= 4, находим корни уравнения х 1 = а + 1, х 2 = а — 3.

При переходе от уравнения (1) к уравнению (2) расширилась область определения уравнения (1), что могло привести к появлению посторонних корней. Поэтому, необходима проверка.

П р о в е р к а. Исключим из найденных значений х такие, при которых

х 1+1=0, х 1+2=0, х2+1=0, х2+2=0.

Если х 1+2=0, то есть (а+1)+2=0, то а = — 3. Таким образом, при а = — 3, х1 — посторонний корень уравнения. (1).

Если х2+1=0, то есть (а – 3) + 1= 0, то а = 2. Таким образом, при а = 2 х2 — посторонний корень уравнения (1).

Если х2+2=0, то есть (а – 3) + 2 = 0, то а=1. Таким образом, при а = 1,

х2 — посторонний корень уравнения (1).

В соответствии с этим при а = — 3 получаем х = — 3 – 3 = -6;

при а = — 2 х = -2 – 3= — 5;

при а = 1 х =1 + 1= 2;

при а = 2 х=2+1 = 3.

Можно записать ответ.

Ответ: 1) если а= -3, то х= -6; 2) если а= -2, то х= -5; 3) если а= 0, то корней нет; 4) если а= 1, то х= 2; 5) если а=2, то х=3; 6) если а ≠ -3, а ≠ -2, а ≠ 0, а≠ 1, а ≠ 2, то х1 = а + 1, х2 = а-3.

§4. Иррациональные уравнения и неравенства

Уравнения и неравенства, в которых переменная содержится под знаком корня, называется иррациональным.

Решение иррациональных уравнений сводится к переходу от иррационального к рациональному уравнению путем возведения в степень обеих частей уравнения или замены переменной. При возведении обеих частей уравнения в четную степень возможно появление посторонних корней. Поэтому при использовании указанного метода следует проверить все найденные корни подстановкой в исходное уравнение, учитывая при этом изменения значений параметра.

Уравнение вида = g ( x ) равносильно системе

Неравенство f ( x ) ≥ 0 следует из уравнения f ( x ) = g 2 ( x ).

При решении иррациональных неравенств будем использовать следующие равносильные преобразования:

≤ g(x) ≥g(x)

Пример 1. Решите уравнение = х + 1 (3)

Это иррациональное уравнение

Решение: По определению арифметического корня уравнение (3) равносильно системе .

При а = 2 первое уравнение системы имеет вид 0 х = 5, то есть не имеет решений.

При а≠ 2 х=. Выясним, при каких значениях а найденное значение х удовлетворяет неравенству х ≥ -1: ≥ — 1, ≥ 0,

откуда а ≤ или а > 2.

Ответ: При а≤, а > 2 х= , при уравнение решений не имеет.

Пример 2. Решить уравнение = а (приложение 4)

Решение. y =

y = а – семейство горизонтальных прямых.

Построим графики функций.

Пример 3 . Решим неравенство (а+1)

Решение. О.Д.З. х ≤ 2. Если а+1 ≤0, то неравенство выполняется при всех допустимых значениях х. Если же а+1>0, то

(а+1)

откуда х (2- 2

Ответ. х (- ;2 при а ( —;-1, х (2- 2

при а ( -1;+).

§ 5. Тригонометрические уравнения и неравенства.

Приведем формулы решений простейших тригонометрических уравнений:

Sinx = a x= (-1) n arcsin a+πn, n Z, ≤1, (1)

Cos x = a x = ±arccos a + 2 πn, , n Z, ≤1. (2)

Если >1, то уравнения (1) и (2) решений не имеют .

tg x = a x= arctg a + πn, n Z, aR

ctg x = a x = arcctg a + πn, n Z, aR

Для каждого стандартного неравенства укажем множество решений:

1. sin x > a arcsin a + 2 πn Z,

при a xR ; при a ≥ 1, решений нет.

при а≤-1, решений нет; при а >1, xR

3. cos x > a — arccos a + 2 πn x arccos a + 2 πn , n Z ,

при а xR ; при a ≥ 1 , решений нет.

при а≤-1 , решений нет ; при a > 1, x R

5. tg x > a, arctg a + πnZ

Пример1. Найти а, при которых данное уравнение имеет решение:

Cos 2 x + 2(a-2)cosx + a 2 – 4a – 5 =0.

Решение. Запишем уравнение в виде

Уравнение cosx = 5- а имеет решения при условии -1≤ 5- а ≤1 4≤ а ≤ 6, а уравнение cosx = — а-1 при условии -1≤ -1- а ≤ 1 -2 ≤ а ≤0.

Ответ. а -2; 0 4; 6

Пример 2. При каких b найдется а такое, что неравенство + b > 0 выполняется при всех х ≠ πn , n Z .

Решение. Положим а = 0. Неравенство выполняется при b >0. Покажем теперь, что ни одно b ≤0 не удовлетворяет условиям задачи. Действительно, достаточно положить х = π /2, если а π /2 при а ≥0.

§ 6. Показательные уравнения и неравенства

1. Уравнение h ( x ) f ( x ) = h ( x ) g ( x ) при h ( x ) > 0 равносильно совокупности двух систем и

2. В частном случае ( h ( x )= a ) уравнение а f ( x ) = а g ( x ) при а > 0, равносильно совокупности двух систем

и

3. Уравнение а f ( x ) = b , где а > 0, a ≠1, b >0, равносильно уравнению

f ( x )= log a b . Случай а =1 рассматриваем отдельно.

Решение простейших показательных неравенств основано на свойстве степени. Неравенство вида f ( a x ) > 0 при помощи замены переменной t = a x сводится к решению системы неравенств а затем к решению соответствующих простейших показательных неравенств.

При решении нестрого неравенства необходимо к множеству решений строгого неравенства присоединить корни соответствующего уравнения. Как и при решении уравнений во всех примерах, содержащих выражение а f ( x ) , предполагаем а > 0. Случай а = 1 рассматриваем отдельно.

Пример 1 . При каких а уравнение 8 х = имеет только положительные корни?

Решение. По свойству показательной функции с основанием, большим единицы, имеем х>0 8 х >1 >1 >0, откуда a (1,5;4).

Ответ. a (1,5;4).

Решение. Рассмотрим три случая:

1. а . Так как левая часть неравенства положительна, а правая отрицательна, то неравенство выполняется для любых х R .

3. а > 0 . a 2 ∙2 x > a 2 x > x > — log 2 a

Ответ. х R при а > 0; решений нет при a =0; х (- log 2 a ; +) при а> 0 .

§ 7. Логарифмические уравнения и неравенства

Приведем некоторые эквивалентности, используемые при решении логарифмических уравнений и неравенств.

В частности, если а >0, а ≠1, то

log a g (x)= log a h(x)

2. Уравнение log a g (x)=b g (x)= a b ( а >0, a ≠ 1, g(x) >0).

3. Неравенство log f ( x ) g ( x ) ≤ log f ( x ) h ( x ) равносильно совокупности двух систем: и

Если а, b – числа, а >0, а ≠1, то

log a f (x) ≤ b

log a f (x) > b

Пример 1. Решите уравнение

Решение. Найдем ОДЗ: х > 0, х ≠ а 4 , a > 0, а ≠ 1. Преобразуем уравнение

log х – 2 = 4 – log a x log х + log a x – 6 = 0, откуда log a x = — 3

х = а -3 и log a x = 2 х = а 2 . Условие х = а 4 а – 3 = а 4 или а 2 = а 4 не выполняется на ОДЗ.

Ответ: х = а -3 , х = а 2 при а ( 0; 1) (1; ).

Пример 2. Найдите наибольшее значение а, при котором уравнение

2 log — + a = 0 имеет решения.

Решение. Выполним замену = t и получим квадратное уравнение 2 t 2 – t + a = 0. Решая, найдем D = 1-8 a . Рассмотрим D ≥0, 1-8 а ≥0 а ≤.

При а = квадратное уравнение имеет корень t = >0.

Ответ. а =

Пример 3 . Решить неравенство log ( x 2 – 2 x + a ) > — 3

Решение. Решим систему неравенств

Корни квадратных трехчленов х 1,2 = 1 ± и х 3,4 = 1 ±.

Критические значения параметра : а = 1 и а = 9.

Пусть Х1 и Х2 – множества решений первого и второго неравенств, тогда

Х 1 Х 2 = Х – решение исходного неравенства.

При 0 a 1 = (- ;1 — )( 1 + ; +), при а > 1 Х 1 = (-;+).

При 0 a 2 = (1 —; 1 +), при а ≥9 Х 2 – решений нет.

Рассмотрим три случая:

1. 0 a ≤1 Х = (1 —;1 — )(1 + ;1 +).

3. a ≥ 9 Х – решений нет.

Высокий уровень С1, С2

Пример 1. Найдите все значения р, при которых уравнение

р ∙ ctg 2 x + 2 sinx + p = 3 имеет хотя бы один корень.

Решение. Преобразуем уравнение

р ∙ ( — 1) + 2 sinx + p = 3, sinx = t , t , t 0.

— p + 2 t + p = 3, + 2 t = 3, 3 -2t = , 3t 2 – 2t 3 = p .

Пусть f ( y ) = 3 t 2 – 2 t 3 . Найдем множество значений функции f ( x ) на . у / = 6 t – 6 t 2 , 6 t — 6 t 2 = 0, t 1 =0, t 2 = 1. f (-1) = 5, f (1) = 1.

При t , E ( f ) = ,

При t , E ( f ) = , то есть при t , E ( f ) = .

Чтобы уравнение 3 t 2 – 2 t 3 = p ( следовательно, и данное) имело хотя бы один корень необходимо и достаточно p E ( f ), то есть p .

Ответ. .

При каких значениях параметра а уравнение log (4 x 2 – 4 a + a 2 +7) = 2 имеет ровно один корень?

Решение. Преобразуем уравнение в равносильное данному:

4 x 2 – 4 a + a 2 +7 = (х 2 + 2) 2 .

Отметим, что если некоторое число х является корнем полученного уравнения, то число – х также является корнем этого уравнения. По условию это не выполнимо, поэтому единственным корнем является число 0.

4∙ 0 2 — 4 a + a 2 +7 = (0 2 + 2) 2 ,

1) a 1 = 1. Тогда уравнение имеет вид: log (4 x 2 +4) =2. Решаем его

4 x 2 + 4 = (х 2 + 2) 2 , 4 x 2 + 4 = х 4 + 4 x 2 + 4, х 4 = 0, х = 0 – единственный корень.

2) a 2 = 3. Уравнение имеет вид: log (4 x 2 +4) =2 х = 0 – единственный корень.

Высокий уровень С4, С5

Пример 3. Найдите все значения р, при которых уравнение

х 2 – ( р + 3)х + 1= 0 имеет целые корни и эти корни являются решениями неравенства: х 3 – 7рх 2 + 2х 2 – 14 рх — 3х +21 р ≤ 0.

Решение. Пусть х 1, х 2 – целые корни уравнения х 2 – ( р + 3)х + 1= 0. Тогда по формуле Виета справедливы равенства х 1 + х 2 = р + 3, х 1 ∙ х 2 = 1. Произведение двух целых чисел х 1 , х 2 может равняться единице только в двух случаях: х 1 = х 2 = 1 или х 1 = х 2 = — 1. Если х 1 = х 2 = 1, то р + 3 = 1+1 = 2 р = — 1; если х 1 = х 2 = — 1, то р + 3 = — 1 – 1 = — 2 р = — 5. Проверим являются ли корни уравнения х 2 – ( р + 3)х + 1= 0 в описанных случаях решениями данного неравенства. Для случая р = — 1, х 1 = х 2 = 1 имеем

1 3 – 7 ∙ (- 1) ∙ 1 2 +2∙ 1 2 – 14 ∙ ( — 1) ∙ 1 – 3 ∙ 1 + 21 ∙ ( — 1) = 0 ≤ 0 – верно; для случая р = — 5, х1 = х2 = — 1 имеем ( — 1) 3 – 7 ∙ ( — 5) ∙ ( -1) 2 + 2 ∙ (-1) 2 – 14 ∙ ( -5) × ( — 1) – 3 ∙ ( — 1) + 21∙ ( -5 ) = — 136 ≤ 0 – верно. Итак, условию задачи удовлетворяют только р = — 1 и р = — 5.

Пример 4. Найдите все положительные значения параметра а, при которых число 1 принадлежит области определения функции

у = ( а — а ).

Решение. у = ( а — а ). Область определения данной функции составляют все значения х, для которых а — а ≥ 0.

Если значения х = 1 принадлежит области определения, то должно выполняться неравенство а— а ≥ 0, а≥ а (1)

Таким образом, необходимо найти все а > 0, удовлетворяющие неравенству (1).

1) а = 1 удовлетворяет неравенству (1).

2) При а > 1 неравенство (1) равносильно неравенству 2 + 5а ≥ а 2 +6,

а 2 — 5а + 4 ≤ 0. Решение этого неравенства: 1≤ а ≤ 4. Учитывая условие а >1, получим 1

а 2 — 5а + 4 ≥ 0. Его решение а ≤ 1; а ≥ 4 с учетом условия 0

Уравнения с параметром — алгоритмы и примеры решения

Общие сведения

Уравнением является любое математическое тождество или физический закон, в котором присутствуют неизвестные величины. Последние необходимо находить. Этот процесс называется поиском корней. Однако не во всех случаях у равенства с переменными бывают решения, а это также нужно доказать.

Корень — величина или диапазон, превращающие искомое выражение в верное равенство. Например, в 5s=10 переменная эквивалентна 2, поскольку только это значение позволяет получить верное тождество, то есть 5*2=10.

Примером диапазона или интервала решений является выражение следующего вида: 0/t=0. Его корнем может быть любое действительное число, кроме нуля. Записывается решение в таком виде: t ∈ (-inf;0)U (0;+inf), где «∈» — знак принадлежности, «-inf» и «inf» — минус и плюс бесконечно большие числа соответственно.

Параметром в уравнении называется некоторая величина, от которой зависит поведение равенства на определенном интервале. Следует отметить, что он также влияет на значение корня, когда входит с ним в различные арифметические операции: сложения, вычитания, умножения, деления, возведения в степень и так далее. Тождества такого типа называют также параметрическими. Далее необходимо разобрать классификацию уравнений.

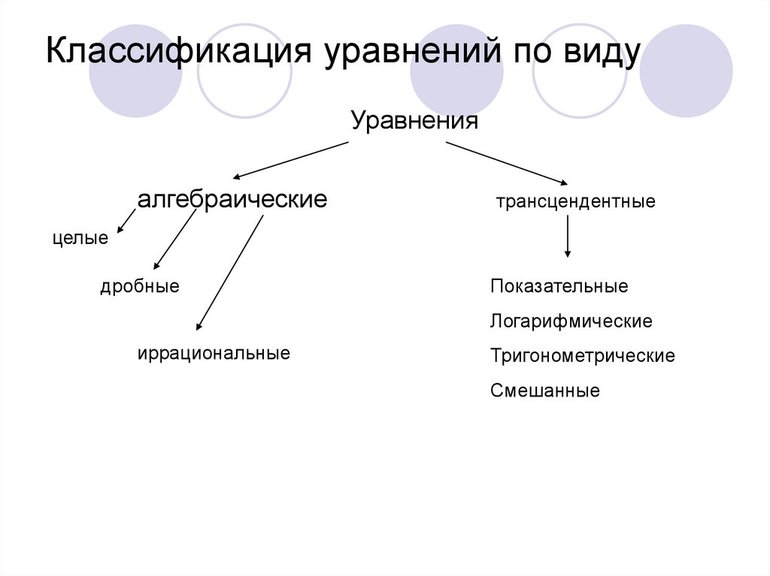
Классификация уравнений

Уравнения делятся на определенные виды, от которых зависит выбор методики их решения. Они бывают следующими: алгебраическими, дифференциальными, функциональными, трансцендентными и тригонометрическими. Кроме того, все они могут содержать некоторую величину — параметр. Его часто обозначают литерой «р» или «а».

Алгебраический тип является наиболее простым, поскольку не содержит сложные элементы. Дифференциальные тождества с неизвестными — одни из самых сложных выражений с точки зрения алгоритма. Они бывают первого, второго, третьего, а также высших порядков. Для нахождения их корней необходимо знать правила дифференцирования и интегрирования.

Практически все функциональные уравнения содержат один или более параметров. Основное их отличие от остальных заключается в функции, которая задается сложным выражением. Последнее может включать несколько неизвестных и параметрических элементов. Примером такого тождества является функция Лапласа, содержащая интеграл обыкновенного типа, а также экспоненту.

К трансцендентным относятся выражения, содержащие показательную, логарифмическую и радикальную (знак корня). Последний тип — тригонометрические. Они содержат любое равенство, содержащее следующие функции: sin, cos, tg и ctg. Однако в математике встречаются также их производные: arcsin, arccos, arcctg, arctg и гиперболические тождества.

Специалисты рекомендуют освоить на начальных этапах обучения методики, позволяющие решать уравнения с параметром линейного типа. После этого можно переходить к более сложным тождествам — функциональным, трансцендентным и так далее.

Алгебраический вид

Алгебраические не содержат в своем составе сложных функций, но в них могут присутствовать компоненты со степенным показателем.

На основании последней характеристики они делятся на 5 типов:

  1. Линейные.
  2. Квадратные (квадратичные).
  3. Кубические.
  4. Биквадратные.
  5. Высших порядков.

Линейные — выражения с переменной, которая имеет только первую степень (равную единице). Если показатель эквивалентен двойке, то такое тождество называется квадратным. В математической интерпретации его еще называют квадратным трехчленом. Когда показатель при неизвестной эквивалентен тройке, тогда это равенство называется кубическим.

Наиболее сложными по своей структуре являются биквадратные (содержат 4 степень). Однако на этом виды линейных уравнений не заканчиваются, поскольку бывают равенства с более высокими показателями. Их называют уравнениями высших порядков. Кроме того, любые тождества могут объединяться в системы уравнений. Их особенностью являются общие решения.

Линейные и квадратичные

Линейное — это самое простое уравнение, которое имеет всего одно решение. Оно решается по следующей методике:

  1. Записывается искомое выражение.
  2. При необходимости раскрываются скобки и приводятся подобные элементы.
  3. Неизвестные (переменные) остаются в левой части тождества, а все константы (числа) — переносятся вправо.
  4. Правая часть сокращается на коэффициент при неизвестной.
  5. Записывается результат.
  6. Выполняется проверка посредством подстановки корня в исходное выражение.

Следует отметить, что линейное выражение с переменной может не иметь решений, поскольку иногда невозможно выполнить операцию сокращения. Например, 0t=85. Равенство не имеет корней, поскольку на нулевое значение делить нельзя, так как при этом получается пустое множество.

Следующим типом является уравнение квадратичной формы At 2 +Bt+C=0. Оно может иметь один или два решения. Однако бывают случаи, при которых корней нет вообще. Для получения результата вводится понятие дискриминанта «D=(-B)^2−4*А*С». Для решения следует воспользоваться следующим алгоритмом:

  1. Записать выражение.
  2. Выполнить при необходимости математические преобразования по раскрытию скобок и приведению подобных слагаемых.
  3. Вычислить значение D (D 0 — два решения).
  4. При D=0 формула корня имеет такой вид: t=-В/(2А).
  5. Если D>0, то решения определяются по следующим соотношениям: t1=[-В-D^(½)]/(2А) и t2=[-В+D^(½)]/(2А).
  6. Записать результат.
  7. Выполнить проверку по отсеиванию ложных корней.

Следует отметить, что ложный корень — значение переменной, полученное по соответствующей формуле, но при подстановке в исходное выражение не выполняет условие равенства нулевому значению.

Кроме того, нужно обратить внимание на типы квадратных уравнений. Они бывают полными и неполными. Первые содержат все коэффициенты (А, В и С), а во вторых — некоторые из них могут отсутствовать, кроме А, так как тогда тождество должно содержать вторую степень при неизвестной.

Неполные решаются методом разложения на множители. Например, «v 2 −81=0» раскладывается следующим образом (формула сокращенного умножения — разность квадратов): (v-9)(t+9)=0. Анализируя последнее равенство, можно сделать вывод о понижении степени. Корнями уравнения являются два значения, t1=-9 и t2=9.

Кубичеcкие и биквадрaтные

Кубические и биквадратные равенства с неизвестным рекомендуется решать при помощи замены переменной. Однако в некоторых случаях можно применить формулы понижения степени или разложения на множители. Иными словами, суть решения алгебраических уравнений, степень которых превышает двойку, сводится к ее понижению различными методами.

Замена переменной производится на другую неизвестную величину. В примере (t 3 −2)+2t 3 −4=0 можно ввести следующий элемент — v=t 3 −2. В результате этого получится равенство такого вида: v+2v=0. Оно решается очень просто:

  1. Приводятся подобные элементы: 3v=0.
  2. Находится корень: v=0.
  3. Приравнивается к выражению, которое заменяли: t 3 −2=0.
  4. Находится корень (один, поскольку у радикала нечетная степень): t=[2]^(1/3).
  5. Проверяется условие: 2^(1/3)^3−2+2*(2^(1/3)^3)-4=4−4=0 (истина).

Биквадратные тождества решаются таким же методом. Однако существует еще один способ — разложение на множители. Его необходимо разобрать на примере решения выражения «4m 4 −324=0». Решать нужно по такому алгоритму:

  1. Упростить (вынести четверку за скобки и сократить на нее): 4 (m 4 −81)=m 4 −81=0.
  2. Разложить на множители (разность квадратов): (m 2 −9)(m 2 +9)=(m-3)(m+3)(m 2 +9)=0/
  3. Решить три уравнения: m1=3, m2=-3, m3=-3 и m4=3.
  4. Результат: m1=-3 и m2=3.
  5. Проверка: 4*(-3)^4−324=0 (истинно) и 4*(3)^4−324=0 (истинно).

Каждый из методов решения выбирается в зависимости от самого уравнения. При чтении условия задачи необходимо определить способ решения. Последний должен быть простым и удобным, а главное — количество шагов решения должно быть минимальным, что существенно сказывается на затраченном времени при вычислениях. Далее нужно рассмотреть подробный алгоритм решения уравнения с параметром.

Пример решения

На основании изученного материала можно приступить к практике решения уравнения с параметром, которое имеет следующий вид: 2v 4 −32−4p-(v 2 +4)+(v-2)(v+2)-v 4 +16=-4, где р — некоторый параметр. Корни и величину р необходимо искать по следующему алгоритму:

  1. Записать равенство с неизвестным и параметром: 2v 4 −32−4p-(v 2 +4)+(v-2)(v+2)-v 4 +16=-4.
  2. Выполнить математические преобразования: 2v 4 −32−4p-v 2 +4+v 2 −4-v 4 +16+4=v 4 −16+4p+4=0.
  3. Ввести замену v 4 −16=m: m+4p+4=0.
  4. Вывести формулу нахождения параметра: р=-(m/4)-1.
  5. Подставить величину m: р=-1-(v 4 +16)/4.
  6. C учетом соотношения равенство будет иметь такой вид: v 4 −16+4[-(v 4 +16−4)/4]+4=-32+8=0 (корней нет, поскольку -24 4 −12=0.
  7. Корни: v1=[12]^(¼) и v2=-[12]^(¼).
  8. Отрицательного корня v2 не существует, поскольку показатель радикала — четное число.
  9. Результат: v1=[12]^(¼).
  10. Проверка: <[12]^(¼)>^4−16+4=16−16=0 (истина).

Следует отметить, что v2 — ложный корень, а также параметр p, равный какому-либо значению, превращает уравнение в пустое множество. Для проверки можно воспользоваться специальным приложением, которое называется онлайн-калькулятором.

Таким образом, уравнения с параметром являются наиболее сложными, поскольку необходимо искать их корни, а также некоторое значение, влияющее на логику выражения. Для их решения необходимо следовать специальному алгоритму, предложенному математиками.

Параметрические уравнения, неравенства и системы, часть С

Теория к заданию 18 из ЕГЭ по математике (профильной)

Параметрические уравнения

Уравнение, которое кроме неизвестной величины содержит также другую дополнительную величину, которая может принимать различные значения из некоторой области, называется параметрическим. Эта дополнительная величина в уравнении называется параметр. На самом деле с каждым параметрическим уравнением может быть написано множество уравнений.

Способ решения параметрических уравнений

  1. Находим область определения уравнения.
  2. Выражаем a как функцию от $х$.
  3. В системе координат $хОа$ строим график функции, $а=f(х)$ для тех значений $х$, которые входят в область определения данного уравнения.
  4. Находим точки пересечения прямой, $а=с$, где $с∈(-∞;+∞)$ с графиком функции $а=f(х)$. Если прямая, а=с пересекает график, $а=f(х)$, то определяем абсциссы точек пересечения. Для этого достаточно решить уравнение вида, $а=f(х)$ относительно $х$.
  5. Записываем ответ.

Общий вид уравнения с одним параметром таков:

При различных значениях, а уравнение $F(x, a) = 0$ может иметь различные множества корней, задача состоит в том, чтобы изучить все случаи, выяснить, что будет при любом значении параметра. При решении уравнений с параметром обычно приходится рассматривать много различных вариантов. Своевременное обнаружение хотя бы части невозможных вариантов имеет большое значение, так как освобождает от лишней работы.

Поэтому при решении уравнения $F(x, a) = 0$ целесообразно под ОДЗ понимать область допустимых значений неизвестного и параметра, то есть множество всех пар чисел ($х, а$), при которых определена (имеет смысл) функция двух переменных $F(x, а)$. Отсюда естественная геометрическая иллюстрация ОДЗ в виде некоторой области плоскости $хОа$.

ОДЗ различных выражений (под выражением будем понимать буквенно — числовую запись):

1. Выражение, стоящее в знаменателе, не должно равняться нулю.

2. Подкоренное выражение должно быть неотрицательным.

3. Подкоренное выражение, стоящее в знаменателе, должно быть положительным.

4. У логарифма: подлогарифмическое выражение должно быть положительным; основание должно быть положительным; основание не может равняться единице.

Алгебраический способ решения квадратных уравнений с параметром $ax^2+bx+c=0$

Квадратное уравнение $ax^2+bx+c=0, а≠0$ не имеет решений, если $D 0$;

Квадратное уравнение имеет один корень, если $D=0$

Тригонометрические тождества

3. $sin^<2>α+cos^<2>α=1$ (Основное тригонометрическое тождество)

Из основного тригонометрического тождества можно выразить формулы для нахождения синуса и косинуса


источники:

http://nauka.club/matematika/algebra/uravneniya-s-parametrom.html

http://examer.ru/ege_po_matematike/teoriya/parametricheskie_uravneniya

© 2023 Русский язык. Привила написания. Наш первый проект тут и тут