Виды условных уравнений в триангуляции при коррелатном способе уравнивания
Рассмотрим условные уравнения, возникающие при уравнивании углов триангуляции. При этом углы редуцированы на плоскость проекции Гаусса-Крюгера и исправлены за центрировку прибора и редукцию визирных целей.
8.1.1 Условие фигур. Сумма измеренных углов в замкнутой фигуре (например, в треугольнике) должна быть равна теоретической.
8.1.2 Условие суммы углов (условие станции). Условие возникает при измерении на станции углов между смежными направлениями и углов, являющихся суммой измеренных углов.
8.1.3 Условие горизонта. Возникает в случаях, когда на станции измерены углы с замыканием горизонта.
8.1.4 Условие полюса (боковое условие). Полюсное условие заключается в требовании, чтобы длина стороны, вычисленная двумя независимыми путями из решения треугольников сети, имела одно и тоже значение.
Примем, что Di = D lg sin bi – изменение lg sin bi при увеличении угла bi на 1”.
8.1.5 Условие исходных дирекционных углов (азимутальное условие). Условие возникает в сети, в которой две или более сторон сети имеют значения дирекционных углов, не подлежащие изменению при уравнивании.
При этом выбор ходовой линии не имеет значения. Частный случай:
8.1.6 Условие базисов возникает в случаях, когда в сети имеется две или более сторон, длины которых не подлежат изменению в процессе уравнивания. Условие базиса заключается в требовании, чтобы длина одной исходной стороны, полученная от другой исходной стороны решением треугольников совпадала с заданным ее значением.
8.1.7 Условие координат возникает в том случае, если в сети имеется два и более разобщенных между собой исходных пункта с координатами, не подлежащими изменению при уравнивании. Для составления уравнений координат из сети выделяют простую и наиболее короткую цепь треугольников, соединяющих два исходных пункта.
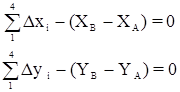
где 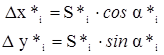
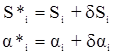
С учетом малости поправок 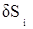
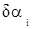
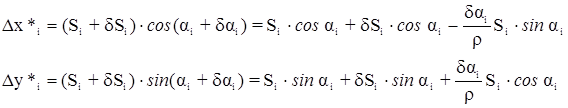
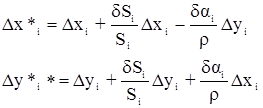
где 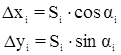
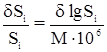
где d lg Si – изменение lg Si, соответствующее поправке 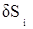
М = 0,43429 – lg e – модуль натуральных логарифмов.
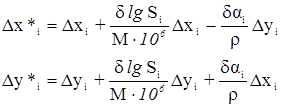
Подставим эти уравнения в исходные условные уравнения и получим:
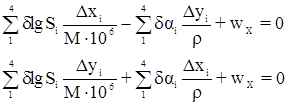
где 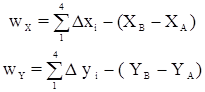
Выразим длины и дирекционные углы ходовой линии через измеренные углы треугольников сети триангуляции:
Из этого следует, что dai и dSi независимы, так как ai вычисляются через промежуточные углы ci, а стороны Si вычисляются при помощи связующих углов ai и bi. Независимость поправок dai и dSi существенно упрощает составление условных уравнений координат. Определим поправки:
d lg S2 = 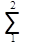
d lg S3 = 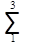
d lg S4 = 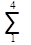
Подставляя dai и d lg Si в условные уравнения получим в окончательном виде:
где 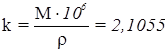
xi, yi – приближенные координаты в км;
Dai, Dbi – изменения lg sin ai и lg sin bi, выраженные в шестом знаке lg;
Дата добавления: 2016-06-02 ; просмотров: 2575 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Виды условных уравнений в триангуляции

webkonspect.com — сайт, с элементами социальной сети, создан в помощь студентам в их непростой учебной жизни.
Здесь вы сможете создать свой конспект который поможет вам в учёбе.
Чем может быть полезен webkonspect.com:
- простота создания и редактирования конспекта (200 вопросов в 3 клика).
- просмотр конспекта без выхода в интернет.
- удобный текстовый редактор позволит Вам форматировать текст, рисовать таблицы, вставлять математические формулы и фотографии.
- конструирование одного конспекта совместно с другом, одногрупником.
- webkonspect.com — надёжное место для хранения небольших файлов.
Виды условных уравнений. Некоторые виды условных уравнений в тригонометрических сетях
| Название | Некоторые виды условных уравнений в тригонометрических сетях |
| Анкор | Виды условных уравнений |
| Дата | 13.01.2022 |
| Размер | 95.78 Kb. |
| Формат файла |  |
| Имя файла | Vidy_uslovnykh_uravneniy.docx |
| Тип | Документы #330099 |
 С этим файлом связано 1 файл(ов). Среди них: КОНТРОЛЬНОЕ ЗАДАНИЕ Психология девиантного поведения.doc. С этим файлом связано 1 файл(ов). Среди них: КОНТРОЛЬНОЕ ЗАДАНИЕ Психология девиантного поведения.doc.  Показать все связанные файлы Подборка по базе: Реферат на тему «Фитнес, виды фитнеса» Курбанова Н.М.docx, 1.3. Виды знаний.pptx, Воображение, его виды и функции.docx, Понятие и виды ценных бумаг — копия.docx, Презентация _Понятие и виды девиантного поведения_.ppt, Решение системы линейных уравнений.docx, Понятие представительства и его виды.ppt, Пример выполнения решения уравнений командой FIND.rtf, Цена, её виды, ценообразование..docx, Понятие сущности и виды денег.docx Показать все связанные файлы Подборка по базе: Реферат на тему «Фитнес, виды фитнеса» Курбанова Н.М.docx, 1.3. Виды знаний.pptx, Воображение, его виды и функции.docx, Понятие и виды ценных бумаг — копия.docx, Презентация _Понятие и виды девиантного поведения_.ppt, Решение системы линейных уравнений.docx, Понятие представительства и его виды.ppt, Пример выполнения решения уравнений командой FIND.rtf, Цена, её виды, ценообразование..docx, Понятие сущности и виды денег.docxРассмотрим виды условий, которые встречаются при уравнивании углов в некоторых простейших фигурах триангуляции. Эти условия будут иметь место в фигурах решенных ниже задач и в заданиях контрольной работы №4. Будем обозначать измеренные значения углов буквами у1, у2, …, уn, а поправки к измеренным значениям углов — буквами υ1, υ2, …,υn. Если в плоском треугольнике измерены и уравнены три угла: 1, 2 и 3 (рис.1), то с уравненными значениями углов условие фигуры будет: Заменив уравненные значения углов измеренными, найдем невязку: Подставив в уравнение (1) вместо уравненных значений углов измеренные значения с соответственными поправками, получим: С учетом (2) условные уравнения фигуры будет иметь вид С должна быть равна 360, т.е. но с измеренными значениями углов получим: Если в уравнение (5) подставить измеренные значения углов с поправками, будем иметь: С учетом уравнения (6) условное уравнение горизонта представится в следующем виде: Условие станции возникает в случае, когда кроме отдельных углов измеряется их сумма (рис.3). При этом должно соблюдаться условие: Условное уравнение станции будет иметь вид: IV. Условие суммы (условие твердого угла) изменению, угол АДС (рис.4), то сумма уравненных углов должна равняться этому твердому углу. В данном Правило составления базисного условного уравнения: 1) выбирают направление подхода от одного базиса к другому (см. рис.4). 2) выписывают номера углов, лежащих против «передних» по ходу сторон в каждом треугольнике (1, 4); 3) то же самое делают для «задних» углов (2, 5); 4) пишут условные уравнения в общем виде типа (15), а затем в линейном виде (16); 5) находят ∆i и вычисляют свободный член (невязки) по формуле (17). Коэффициенты ∆i и невязку Wi вычисляют в специальной таблице. V Условие полюса возникает в том случае, когда из одной точки, называемой полюсом, измерены направления на все вершины какой-либо замкнутой фигуры (рис.5). Сущность его заключается в том, что в результате последовательного решения треугольников необходимо получить из решения последнего треугольника то же значение исходной стороны, которое было принято при решении первого треугольника. Полюсное условие составляется так, как и базисное (сторон), но базисы в вычислениях не участвуют. В центральной системе (рис.5) полюсом может быть, как центральная точка 0, так и любая из остальных точек А, В, С. Если принять за полюс точку 0, то условное уравнение в линейном виде представляется формулой: г источники: http://webkonspect.com/?room=profile&id=25292&labelid=226493 http://topuch.ru/nekotorie-vidi-uslovnih-uravnenij-v-trigonometricheskih-setyah/index.html |
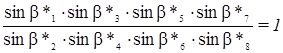
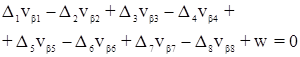
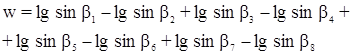
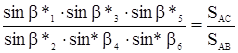
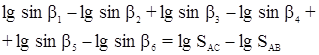
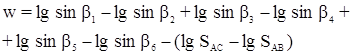
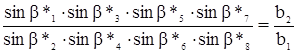
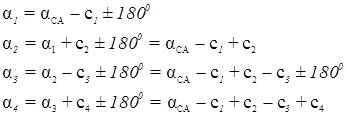
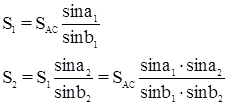
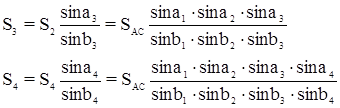

 . Условие фигуры (треугольника)
. Условие фигуры (треугольника) умма уравненных углов при точке 0 (рис.2)
умма уравненных углов при точке 0 (рис.2) III. Условие станции
III. Условие станции Если при точке Д дан твердый, т.е. не подлежащий
Если при точке Д дан твердый, т.е. не подлежащий I. Условие полюса
I. Условие полюса де . (19)
де . (19)