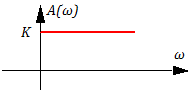Виды звеньев и их уравнения — Решение уравнений

3. Частотные характеристики звеньев и систем автоматического управления. ч. 3.2 Простейшие типовые звенья

Лекции по курсу «Управление Техническими Системами» читает Козлов Олег Степанович на кафедре «Ядерные реакторы и энергетические установки» факультета «Энергомашиностроения» МГТУ им. Н.Э. Баумана. За что ему огромная благодарность!

Данные лекции готовятся к публикации в виде книги, а поскольку здесь есть специалисты по ТАУ, студенты и просто интересующиеся предметом, то любая критика приветствуется.

Тема сегодняшней статьи:
3.2. Типовые звенья систем автоматического управления (регулирования). Классификация типовых звеньев. Простейшие типовые звенья.

Хочешь вкусить плодов познания? — Грызи гранит науки!

Понятие “типовые звенья” в теории управления техническими системами, в основном, связано с описанием САУ (САР) в переменных “вход – выход”, т.е. описание систем в передаточных функциях. Любую линейную САУ (САР) или линеаризованную САР можно структурно расчленить на простейшие элементы (звенья), соединенные между собой соответствующими последовательными, параллельными связями, местными и локальными обратными связями, сумматорами, сравнивающими устройствами и т.д.

Достигнуто общепринятое соглашение, что наиболее удобно расчленять структурную схему САР на звенья 1-го и 2-го порядков. Принято называть такие простейшие звенья типовыми.

С другой стороны, реальная линеаризованная (линейная) система состоит из набора отдельных узлов и агрегатов, соединенных соответствующими связями, причем порядок уравнений динамики вышеуказанных узлов и агрегатов может быть и выше второго. В этом случае звенья (узлы и агрегаты) САР можно классифицировать по их свойствам.

Различают 3 типа звеньев:

Существуют также особые звенья, которые будут рассмотрены позднее.

Учитывая, что передаточная функция линейного (линеаризованного) звена может быть записана как:

где: и — полиномы по степеням s, причем коэффициенты при низшей степени s в полиномах , равны 1, классификацию на типы звеньев можно объяснить видом полиномов или (что эквивалентно) видом коэффициентов в соответствующих уравнениях динамики звена.
Подробнее о передаточной функции см. здесь.

Позиционным звеном считают звено, в котором полиномы N(s) и L(s) содержат свободные члены (равные 1). Например:

или в уравнении динамики (x(t) – входной сигнал, y(t) – выходной):

Из типовых звеньев (1-го и 2-го порядка) к позиционным звеньям относятся: идеальное усилительное звено, апериодические звенья 1-го и 2-го порядка, колебательное звено и форсирующее звено.

Дифференцирующим звеном считается звено, в котором полином L(s) содержит свободный член (равный 1), а полином N(s) не содержит свободного члена ().
Например:

или в уравнении динамики:

Из типовых звеньев к дифференцирующим звеньям относятся идеальное дифференцирующее звено, инерционно-дифференцирующее звено.

Интегрирующим звеном считается звено, в котором полином N(s) содержит свободный член (), а полином L(s), не содержит свободного члена (). Например:

или в уравнении динамики:

Из типовых звеньев к интегрирующим звеньям относятся идеальное интегрирующее звено, инерционно–интегрирующее звено.

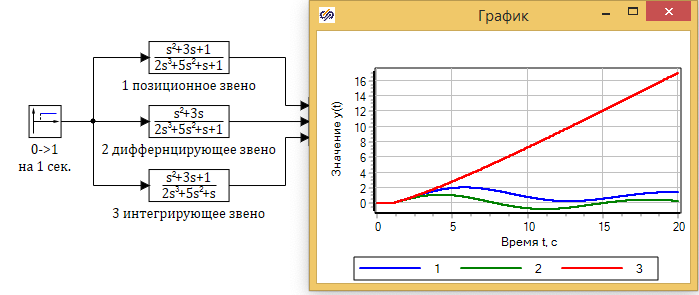
Пример переходного процесса при единичном ступенчатом воздействии на три разных звена, приведенных выше:

3.2.1. Идеальное усилительное звено

Уравнение динамики каждого звена имеет вид: , т.е. уравнение не является дифференциальным, следовательно, данное звено является безынерционным.

Переходя к изображениям , получаем:
– уравнение динамики звена в изображениях.
Передаточная функция идеального усилительного звена:

АФЧХ не зависит от ω, поскольку:

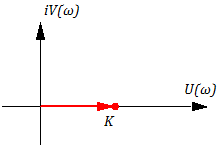
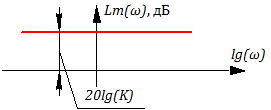
Рисунок 3.2.1 АФЧХ идеального усилительного звена

Годограф АФЧХ “вырождается” в точку: U(ω) =K; V(ω) =0;
A(ω) ≡modW(iω) =│W(iω)│=K =>
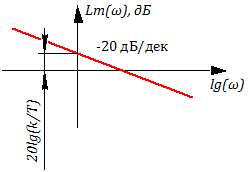
Lm(ω)=20lgA(ω) =20lgK; =>
φ(ω) = const = 0 т.е. фазового сдвига нет. Следовательно, данное звено является безынерционным, чисто усилительным звеном.

Рисунок 3.2.4 ЛАХ идеального усилительного звена

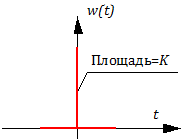
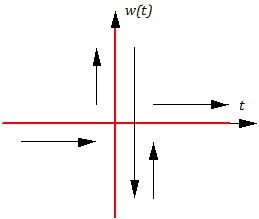
Найдем весовую w(t) и переходную h(t) функции звена (подробнее см. здесь).
Весовая функция:

3.2.2. Идеальное дифференцирующее звено

Уравнение динамики звена имеет вид:

где: – постоянная времени.

Переходя к изображениям:

Уравнение динамики звена в изображениях:

Передаточная функция идеального дифференцирующего звена:

Графики годографа АФЧХ, A(ω) и φ(ω) имеют вид:

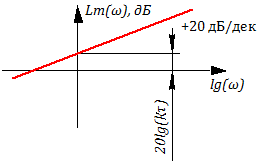
Логарифмическая амплитудная характеристика ЛАХ::

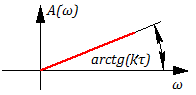
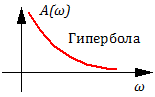
Из рисунка 3.2.9 видно, что данное звено обеспечивает опережение по фазе на /2 (при любой частоте входного сигнала).

Чем выше частота единичного гармонического сигнала на входе в звено, тем выше амплитуда выходного сигнала в установившемся режиме.

Найдем весовую функцию звена:

Учитывая, что δ(t) имеет вид как на рис.3.2.11 (зависимость показана утрированно), а весовая функция пропорциональна производной от δ(t):

Найдем переходную функцию звена:

Иногда идеальное дифференцирующее звено представляется в виде или . В последнем варианте коэффициент К имеет смысл постоянной времени.

3.2.3. Идеальное интегрирующее звено

Уравнение динамики такого звена имеет вид:

или в изображениях:

Передаточная функция идеального интегрирующего звена:

Умножая числитель и знаменатель на i, получаем:

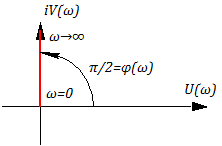
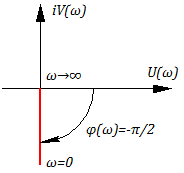
Годограф АФЧХ имеет вид:

Данное звено всегда дает отставание по фазе на угол .

Найдем весовую функцию звена:

Найдем переходную функцию звена:

Примерами устройств, близких к идеальному усилительному звену, можно считать: широкополосный электронный усилитель (приближенно), механический редуктор без учета инерционности и нелинейных эффектов, жесткую механическую муфту и т.д.

Примером идеального дифференцирующего звена можно считать тахогенератор:

где u(t) – напряжение на клеммах тахогенератора, φ(t) – угол поворота якоря (ротора) тахогенератора.

Примером идеального интегрирующего звена можно считать большинство электродвигателей (без учета инерционности якоря), где входным воздействием считать напряжение в обмотке возбудителя (двигателем постоянного тока), а выходным воздействием – угол поворота выходного вала.

Пример интегрирующего и дифференцирующего звена на основе конденсатора

Один и тот же технический элемент, с точки зрения теории автоматического управления, может выступать как в качестве интегрирующего, так и в качестве дифференцирующего звена.

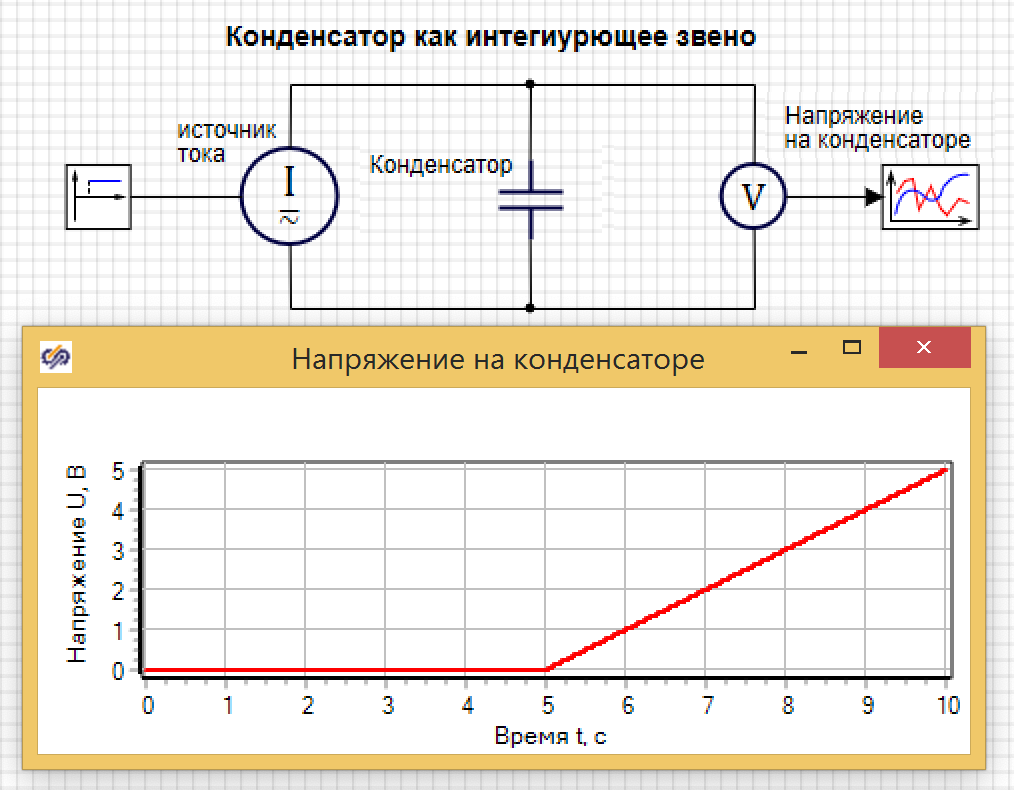
В качестве примера интегрирующего звена можно рассмотреть конденсатор, где входным воздействием является ток, а выходным результатом является напряжение на клеммах конденсатора. Действительно, при малом токе и большой емкости конденсатора, в случае ступенчатого изменения тока с 0, мы получаем график напряжения, совпадающий по форме с переходной функцией интегрирующего звена. На рисунке 3.2.20 представлена такая модель, где ток ступенькой меняется на пятой секунде расчета.

Если построить с помощью гармонического анализатора ЛАХ и ФЧХ, мы увидим, что угол наклона ЛАХ составляет -20 dB/dec, а угол сдвига фазы равен — или -90 градусов на графике (см. рис. 3.2.21).

Тот же самый конденсатор, при определенных параметрах сети, может выступать в качестве идеального дифференцирующего звена, если в качестве входного воздействия подавать напряжение, а в качестве результирующей величины использовать ток в цепи.

Электрическая схема использования конденсатора в качестве дифференцирующего звена с гармоническим анализатором приведена на рисунке 3.2.22. На графиках гармонического анализатора видно, что угол наклона ЛАХ составляет 20 dB/dec, а угол сдвига фазы равен или 90 градусов на графике.

Примеры моделей, использованные в данной лекции, можно взять в этом архиве.

Лекция №3. Динамические звенья и их характеристики

Лекция №3. ДИНАМИЧЕСКИЕ ЗВЕНЬЯ И ИХ ХАРАКТЕРИСТИКИ

3.1. Общие положения

Для создания общей методики расчета различных систем автоматического регулирования удобно ввести понятие динамического звена. Под динамическим звеном понимают устройство любого физического вида и конструктивного содержания, описываемое определённым дифференциальным уравнением.

В соответствии с этим классификация звеньев производится именно по виду дифференциального уравнения. Одним и тем же уравнением могут описываться весьма разнообразные устройства (механические, электрические, гидравлические и т. д.). Для ТАУ это будет один и тот же тип звена.

Обозначим входную величину звена через х1, выходную – через х2, а возмущающее воздействие – через DF (рис. 2.2).

Статическая характеристика любого звена может быть изображена в виде прямой линии (рис. 3.1), так как пока рассмотрим только линейные, или точнее линеаризованные системы.

В звеньях позиционного или статического типа линейной зависимостью х2 = k х1 связаны выходная и входная величины в установившемся режиме (рис. 3.1, а). Коэффициент пропорциональности между выходной и входной величинами представляет собой коэффициент передачи.

Рис. 3.1. Характеристики позиционных звеньев

В звеньях интегрирующего типа линейной зависимостью связаны производная выходной величины и входная величина в установившемся режиме (рис. 3.1, б). В этом случае для установившегося режима будет справедливым равенство , откуда и произошло название этого типа звеньев. Коэффициент пропорциональности k называется коэффициентом передачи звена. В случае, если входная и выходная величины звена имеют одинаковую размерность, коэффициенту передачи соответствует размерность – секунда в минус первой степени (с-1).

В звеньях дифференцирующего типа, в установившемся режиме, линейной зависимостью связаны выходная величина и производная входной (рис. 3.1, в), откуда и произошло название этого типа звеньев. Коэффициент пропорциональности называется коэффициентом передачи звена. Если входная и выходная величины имеют одинаковую размерность, коэффициенту передачи соответствует размерность – секунда (с).

Как уже отмечалось, классификация звеньев производится по виду дифференциального уравнения или, что все равно, по виду передаточной функции звена. Предположим, что звено, изображенное на рис. 2.1, описывается дифференциальным уравнением, представленным в стандартной форме записи

. (3.1)

При нулевых начальных условиях (то есть при t

Типовые динамические звенья и их характеристики

Типовые динамические звенья- это минимально необходимый набор звеньев для описания системы управления произвольного вида.

Типы звеньев систем управления различаются по виду их передаточной функции (или дифференциального уравнения), определяющей все их динамические свойства и характеристики. Классификация основных типов динамических звеньев приведена на рис.3.9.

Основные типы звеньев делятся на четыре группы: позиционные, интегрирующие, дифференцирующие и неминимально-фазовые [1,2]. Позиционные, интегрирующие и дифференцирующие звенья относятся к минимально-фазовым. Важным свойством минимально-фазовых звеньев является однозначное соответствие амплитудной и фазовой частотных характеристик. Другими словами, по заданной амплитудной характеристике всегда можно определить фазовую и наоборот.

Позиционные звенья

В звеньях позиционного, или статического типа, линейной зависимостью y = kx связаны выходная и входная величины в установившемся режиме. Коэффициент пропорциональности k между выходной и входной величинами представляет собой коэффициент передачи звена. Позиционные звенья обладают свойством самовыравнивания, то есть способностью самостоятельно переходить в новое установившееся состояние при ограниченном изменении входного воздействия.

Рис. 3.9. Классификация типовых динамических звеньев

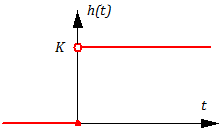
Безынерционное (идеальное усилительное) звено.Это звено не только в статике, но и в динамике описывается алгебраическим уравнением

Амплитудно-фазовая частотная характеристика:

W(jw) = k, A(w) = k, y(w) = 0. (3.16)

Переходная и импульсная функции:

h(t) = k1(t), w(t) = kd(t). (3.17)

Безынерционное звено является некоторой идеализацией реальных звеньев. В действительности ни одно звено не в состоянии равномерно пропускать все частоты от 0 до ¥.

Примерами таких безынерционных звеньев могут служить жесткая механическая передача, часовой редуктор, электронный усилитель сигналов на низких частотах и др.

Апериодическое (инерционное) звено первого порядка.Уравнение и передаточная функция звена:

(Tp+1) y(t) = x(t), , (3.18)

где T — постоянная времени, характеризует степень инерционности звена, т.е. длительность переходного процесса.

Амплитудно-фазовая частотная характеристика:

W(jw) = 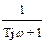, , y(w) = — arctgTw. (3.19)

Таким образом, апериодическое звено первого порядка является фильтром низких частот.

Переходная и импульсная функции:

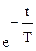
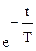
h(t) = (1 — ), w(t) = . (3.20)

Примерами апериодического звена первого порядка могут служить RC цепочка, нагревательный элемент и др.

Апериодическое (инерционное) звено второго порядка.Дифференциальное уравнение звена имеет вид

, (3.21)

причем предполагается, что 2Т₂£ Т₁.

В этом случае корни характеристического уравнения вещественные и уравнение (3.21) можно переписать в виде:

где — новые постоянные времени.

Передаточная функция звена

. (3.23)

Из выражения (3.23) следует, что апериодическое звеновторого порядка можно рассматривать как комбинацию двух апериодических звеньев первого порядка.

Примерами апериодического звена второго порядка могут служить двойная RC цепочка, электродвигатель постоянного тока и др.

Колебательное звено.Описывается дифференциальным уравнением

, (3.24)

при Т₁ 2 p 2 +2xTp+1) y(t) = x(t), (3.25)

где Т — постоянная времени, определяющая угловую частоту свободных колебаний l=1/Т;

x — параметр затухания, лежащий в пределах 0

Амплитудно-фазовая характеристика совпадает с вещественной осью. При 0 1/T — с отрицательной полуосью.

Временные характеристики соответствуют незатухающим колебаниям с угловой частотой 1/T.

Интегрирующие звенья

В звеньях интегрирующего типа линейной зависимостью связаны в установившемся режиме производная выходной величины и входная величина. В этом случае для установившегося режима будет справедливым равенство , откуда и произошло название этого типа звеньев.

Идеальное интегрирующее звено.Уравнение и передаточная функция имеют вид

py(t) = x(t), . (3.28)

Амплитудно-фазовая частотная характеристика:

W(jw) = , A(w) = , y(w) = -90 0 . (3.29)

Переходная и импульсная функции:

h(t) = t, w(t) = 1(t). (3.30)

Такое звено является идеализацией реальных интегрирующих звеньев.

Примерами идеальных интегрирующих звеньев могут служить операционный усилитель в режиме интегрирования, гидравлический двигатель, емкость и др.

Дифференцирующие звенья

В звеньях дифференцирующего типа линейной зависимостью связаны в установившемся режиме выходная величина и производная входной, откуда и произошло название этого типа звеньев.