Вольфрам альфа уравнение в частных производных

WolframAlpha по-русски

Математика с WolframAlpha ® . Объяснения с примерами.

Дифференцирование функций в Wolfram|Alpha

Как найти производную функции в Wolfram|Alpha?

Wolfram|Alpha использует для дифференцирования функций несколько различных запросов. Проще всего найти обычную производную функции f(x) в Wolfram|Alpha можно с помощью запроса-префикса d/dx.

Вот, как это выглядит на практике

Чтобы получить пошаговое решение с пояснениями каждого шага, достаточно нажать «Show steps».

Для вычисления производных второго порядка служит запрос d^2/dx^2:

Аналогично вычисляются производные высших порядков. Например, так вычисляется производная третьего порядка:

Wolfram|Alpha может находить сразу производные нескольких порядков. Как, например, это может понадобиться при отыскании коэффициентов ряда Тейлора. Для этого используется запрос на табуляцию функции с указанием наименьшего, наибольшего порядка производной, а также шага между ними. Чтобы не загромождать изложение, рассмотрим простой пример на вычисление производных функции cos(x) до 5-го порядка включительно:

Тот же результат (табулирование производной) получим по запросу вида

Для вычисления значения производной в заданной точке, нужно указать значение аргумента:

Частные производные вычисляются аналогично:

Естественно, с помощью Wolfram|Alpha можно визуально сравнить функцию и ее производную:

Конечно, навряд ли можно научиться дифференцировать функции, используя исключительно Wolfram|Alpha. Однако, система Wolfram|Alpha вполне подходит, чтобы проверить свои знания, освежить их, например, перед экзаменом, и убедиться, что вы к нему вполне готовы.

Преподавателям Wolfram|Alpha поможет оценить сложность и время на выполнение заданий на производные, которые предлагаются студентам.

Вольфрам альфа уравнение в частных производных

1. Решение рациональных, дробно-рациональных уравнений любой степени, показательных, логарифмических, тригонометрических уравнений.
Пример 1 . Чтобы решить уравнение x 2 + 3 x — 4 = 0, нужно ввести solve x^2+3x-4=0
Пример 2. Чтобы решить уравнение log₃2x = 2 , нужно ввести solve log(3, 2x)=2
Пример 3. Чтобы решить уравнение 25 x-1 = 0.2 , нужно ввести solve 25^(x-1)=0.2
Пример 4. Чтобы решить уравнение sin x = 0.5 , нужно ввести solve sin(x)=0.5

2. Решение систем уравнений.
Пример . Чтобы решить систему уравнений

нужно ввести solve x+y=5 && x-y=1
Знаки && в данном случае обозначает логическое «И».

3. Решение рациональных неравенств любой степени.
Пример . Чтобы решить неравенство x 2 + 3 x — 4 solve x^2+3x-4

4. Решение систем рациональных неравенств.
Пример. Чтобы решить систему неравенств

нужно ввести solve x^2+3x-4 && 2х^2 — x + 8 > 0
Знаки && в данном случае обозначает логическое «И».

5. Раскрытие скобок + приведение подобных в выражении.
Пример . Чтобы раскрыть скобки в выражении (c+d) 2 (a-c) и привести подобные, нужно
ввести expand (c+d)^2*(a-c) .

6. Разложение выражения на множители.
Пример . Чтобы разложить на множители выражение x 2 + 3 x — 4, нужно ввести factor x^2 + 3x — 4 .

7. Вычисление суммы n первых членов последовательности (в том числе арифметической и геометрической прогрессий).
Пример . Чтобы вычислить сумму 20 первых членов последовательности, заданной формулой a_n = n 3 +n, нужно ввести sum n^3+n, n=1..20
Если нужно вычислить сумму первых 10 членов арифметической прогрессии, у которой первый член a ₁ = 3, разность d = 5, то можно, как вариант, ввести a1=3, d=5, sum a1 + d(n-1), n=1..10
Если нужно вычислить сумму первых 7 членов геометрической прогрессии, у которой первый член b ₁ = 3, разность q = 5, то можно, как вариант, ввести b1=3, q=5, sum b1*q^(n-1), n=1..7

8. Нахожд ение производной.
Пример . Чтобы найти производную функции f(x) = x 2 + 3 x — 4, нужно ввести derivative x^2 + 3x — 4

9. Нахожд ение неопределенного интеграла.
Пример . Чтобы найти первообразную функции f(x) = x 2 + 3 x — 4, нужно ввести integrate x^2 + 3x — 4

10. Вычисление определенного интеграла.
Пример . Чтобы вычислить интеграл функции f(x) = x 2 + 3 x — 4 на отрезке [5, 7],
нужно ввести integrate x^2 + 3x — 4, x=5..7

11. Вычисление пределов.
Пример . Чтобы убедиться, что

введите lim (x -> 0) (sin x)/x и посмотрите ответ. Если нужно вычислить какой-то предел при x, стремящемся к бесконечности, следует вводить x -> inf .

12. Исследование функции и построение графика .
Пример . Чтобы исследовать функцию x 3 — 3 x 2 и построить ее график, просто введите x^3-3x^2 . Вы получите корни (точки пересечения с осью ОХ), производную, график, неопределенный интеграл, экстремумы.

13. Нахождение наибольшего и наименьшего значений функции на отрезке .
Пример . Чтобы найти минимальное значение функции x 3 — 3 x 2 на отрезке [0.5, 2],
нужно ввести minimize (x^3-x^2),
Чтобы найти максимальное значение функции x 3 — 3 x 2 на отрезке [0.5, 2],
нужно ввести maximize (x^3-x^2),

Рубрика «уравнения в частных производных»

Обзор новых возможностей Mathematica 11 и языка Wolfram Language

Перевод поста Стивен Вольфрам (Stephen Wolfram) «Today We Launch Version 11!».
Выражаю огромную благодарность Полине Сологуб за помощь в переводе и подготовке публикации

Содержание

Я рад объявить о выходе новой версии системы Mathematica и 11-й версии языка Wolfram Language, доступной как для Desktop-компьютеров, так и в облачном виде. В течение последних двух лет сотни человек упорно трудились над ее созданием, а несколько тысяч часов и я лично. Я очень взволнован; это важный шаг вперед, имеющий важное значение для многих крупнейших технологических областей.

Прошло больше 28 лет с тех пор, как вышла 1-я версия, — и почти 30 лет с тех пор, как я занялся ее разработкой. И все это время я продолжал воплощать дерзкую мечту — строить все больший и больший стек технологий. Большая часть программного обеспечения спустя несколько лет и несколько версий, за исключением мелких доработок, практически не меняется. С системой Mathematica и Wolfram Language сложилась совсем другая история: в течение трех десятилетий мы c каждой новой версией продвигались вперед, завоевывая постепенно огромное количество новых областей.
Читать полностью »

Новое в Wolfram Language | Аналитическое решение уравнений в частных производных

Перевод поста Devendra Kapadia «New in the Wolfram Language: Symbolic PDEs».
Код, приведенный в статье, можно скачать здесь.
Выражаю огромную благодарность Кириллу Гузенко KirillGuzenko за помощь в переводе и подготовке публикации.

Уравнения в частных производных (УрЧП) играют очень важную роль в математике и ее приложениях. Их можно использовать для моделирования реальных явлений, таких как колебания натянутой струны, распространения потока тепла в стержне, в финансовых областях. Цель этой статьи — приоткрыть завесу в мир УрЧП (тем кто еще с ним не знаком) и ознакомить читателя с тем, как можно эффективно решать УрЧП в Wolfram Language, используя новый функционал для решения краевых задач в DSolve, а так же новую функцию DEigensystem, которая появилась в версии 10.3.

История УрЧП восходит к работам известных математиков восемнадцатого века — Эйлера, Даламбера, Лапласа, однако развитие этой области в последние три столетия так и не остановилось. И потому в статье я приведу как классические, так и современные примеры УрЧП, что позволит рассмотреть эту область знаний под разными углами.

Давайте начнем с рассмотрения колебаний натянутой струны с длиной π, закрепленной на обоих концах. Колебания струны можно смоделировать с помощью одномерного волнового уравнения, приведённого ниже. Здесь u(x,t) — вертикальное смещение точки струны с координатой х в момент времени t:

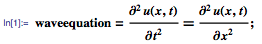
Читать полностью »