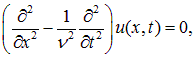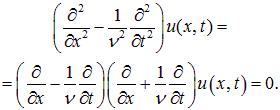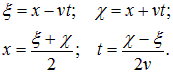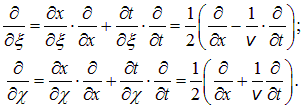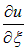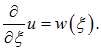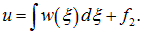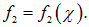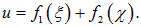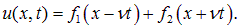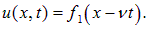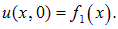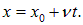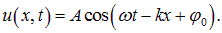Волновое уравнение и его общее решение

2.2. Решение волнового уравнения

Уравнение типа (2.2), описывающее колебания различных упругих сред, называется волновым уравнением. Запишем его формально в виде:

Введем теперь вместо (x, t) новые переменные:

Производные по новым переменным выражаются по стандартным правилам дифференцирования сложной функции:

Отсюда следует, что уравнение (2.16) в новых переменных записывается в виде:

Поскольку производная по равна нулю,

не зависит от этой переменной и, следовательно, является некоторой функцией w только от переменной :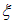

Интегрируем теперь это уравнение:

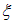
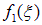
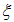
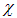
Первое слагаемое в правой части является только функцией переменной , которую мы обозначим как . Второе слагаемое — постоянная интегрирования. Она не зависит от , являясь, стало быть, функцией только переменной :

Мы получили, что решение волнового уравнения имеет вид:

Подставляя сюда выражения (2.17), мы возвращаемся к прежним переменным (x, t):

Функции f₁ и f₂ — совершенно произвольны и должны быть определены из начальных и граничных условий.

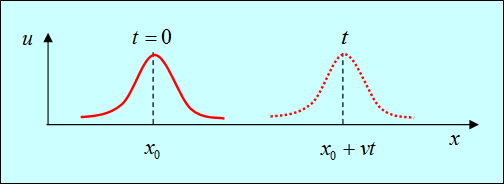
Обсудим физический смысл полученных решений. Ограничимся сначала первым слагаемым. Пусть

В момент времени t = 0 функция f₁(x) задает распределение смещений (профиль струны, деформацию твердого тела, распределение давления или частиц в газе и т. д.):

Предположим, например, что это распределение имеет максимум в точке 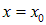(рис. 2.6).

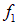
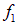
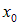
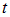
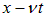
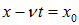
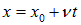
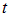
Такое распределение называют обычно волновым пакетом. В момент t максимум функции по-прежнему будет в точке, в которой аргумент равен , но теперь (в момент времени ) аргумент равен , таким образом: или . Другими словами, за время от 0 до волновой пакет сдвинется вправо на расстояние vt, так что максимум теперь придется на точку

Нетрудно сообразить, что форму свою волновой пакет при этом перемещении не изменит.

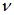
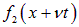
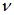
Мы видим, что начальное распределение движется вправо со скоростью . Аналогично, второе слагаемое, , описывает движение волнового пакета налево с той же скоростью . Общее решение (2.21) является суперпозицией двух этих решений.

В свою очередь, любой волновой пакет может быть представлен как суперпозиция гармонических функций. Отсюда — особая роль решений волнового уравнения вида:

Это решение описывает монохроматическую волну, распространяющуюся направо со скоростью

Волновое уравнение

Вы будете перенаправлены на Автор24

В том случае если волна распространяется в однородной среде, то ее движение в общем случае описывают волновым уравнением (дифференциальным уравнением в частных производных):

где $v$ — фазовая скорость волны $\triangle =\frac<<\partial >^2><\partial x^2>+\frac<<\partial >^2><\partial y^2>+\frac<<\partial >^2><\partial z^2>$ — оператор Лапласа. Решением уравнения (1,2) служит уравнение любой волны, данные уравнения удовлетворяют, например, и плоская и сферическая волны.

Если плоская волна распространяется вдоль оси $X$, то уравнение (1) представляется как:

Если физическая величина распространяется как волна, то она обязательно удовлетворяет волновому уравнению. Справедливо обратное утверждение: если какая — либо величина подчиняется волновому уравнению, то она распространяется как волна. Скорость распространения волны будет равна квадратному корню из коэффициента, который стоит при сумме пространственных производных (в данном виде записи).

Волновое уравнение играет очень большую роль в физике.

Решение волнового уравнения для плоской волны

Запишем общее решение уравнения (2), для световой волны, распространяющейся в вакууме в случае, если s скалярная функция зависит только от одной из декартовых переменных, например $z$, то есть $s=s(z,t)$, что означает, функция $s$ имеет постоянное значение в точках плоскости, которая перпендикулярна $оси Z$. Волновое уравнение (1) в этом случае примет вид:

Готовые работы на аналогичную тему

где скорость распространения света в вакууме равна $c$.

Общим решением уравнения (4) при заданных условиях будет выражение:

где $s_1\left(z+ct\right)$- функция описывающая волну произвольной формы, которая перемещается со скоростью $c$ в отрицательном направлении по отношению к направлению $оси Z$, $s_2\left(z-ct\right)$ — функция описывающая волну произвольной формы, которая перемещается со скоростью $c$ в положительном направлении по отношению к направлению $оси Z$. Надо отметить, что в процессе движения значения $s_1$ и $s_2$ в любой точке волны и ее форма волны неизменны.

Получается, что волна, которую описывает суперпозиция двух волн (в соответствии с формулой (5)). Причем эти составляющие волны движутся в противоположных направлениях. В этом случае уже нельзя говорить о скорости или направлении волны. В самом простом случае получается стоячая волна. В общем случае необходимо рассматривать сложное электромагнитное поле.

Волновое уравнение и система уравнений Максвелла

Волновые уравнения для колебаний векторов напряженности электрического поля и вектора магнитной индукции магнитного поля легко получить из системы уравнений Максвелла в дифференциальной форме. Запишем систему уравнений Максвелла для вещества, в котором нет свободных зарядов и токов проводимости:

Применим операцию $rot$ к уравнению (7):

В выражении (10) можно изменить порядок дифференцирования в правой части выражения, так как пространственные координаты и время — независимые переменные, следовательно, имеем:

Примем во внимание то, уравнение (6), заменим $rot\overrightarrow$ в выражении (11) на правую часть формулы (6), имеем:

Зная, что $rotrot\overrightarrow=graddiv\overrightarrow—<\nabla >^2\overrightarrow$, и используя $div\overrightarrow=0$, получаем:

Аналогично можно получить волновое уравнение для вектора магнитной индукции. Оно имеет вид:

В выражениях (13) и (14) фазовая скорость распространения волны $(v)$ равна:

Задание: Получите общее решение волнового уравнения $\frac<<\partial >^2s><\partial z^2>-\frac<1>\frac<<\partial >^2s><\partial t^2>=0(1.1)$ плоской световой волны.

Решение:

Введем независимые переменные вида для функции $s$:

\[\xi =z-ct,\ \eta =z+ct\left(1.2\right).\]

В таком случае частная производная $\frac<\partial s><\partial z>$ равна:

Частная производная $\frac<\partial s><\partial t>$ равна:

Вычтем почленно выражение (1.4) из выражения (1.3), имеем:

Почленное сложение выражений (1.4) и (1.3) дает:

Найдем произведение левых частей выражений (1.5) и (1.6) и учтем результаты, записанные в правых частях этих выражений:

Если проинтегрировать выражение (1.7) по $\xi $, то получим функцию, которая не зависит от этой переменной, и может зависеть только от $\eta $, что значит, что она является произвольной функцией $\Psi(\eta )$. В этом случае уравнение (1.7) примет вид:

Проведем интегрирование (1.8) по $\eta $ имеем:

где $s_1\left(з\right)$ — первообразная, $s_2\left(\xi \right)$- постоянная интегрирования. Причем, функции $s_1$ и $s_2$ — произвольные. Учитывая выражения (1.2), общее решение уравнения (1.1) можно записать как:

Ответ: $s\left(z,t\right)=s_1\left(z+ct\right)+s_2\left(z-ct\right).$

Задание: Определите из волнового уравнения, чему равна фазовая скорость распространения плоской световой волны.

Решение:

Сравнивая волновое уравнение, например, для вектора напряженности, полученное из уравнений Максвелла:

с волновым уравнением:

позволяет сделать вывод о том, что скорость распространения волны $(v)$ равна:

Но здесь требуется отметить, что понятие скорости электромагнитной волны имеет определенный смысл только с волнами простой конфигурации, под такие волны подходит, например категория плоских волн. Так $v$ не будет являться скоростью распространения волны в случае производного решения волнового уравнения, в состав которых входят, например, стоячие волны.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 26 02 2021

Волновое уравнение движущейся волны

Физика > Математическое отображение движущейся волны

Волновое уравнение – математическая формула движения волны. Рассмотрите, как вывести решение волнового уравнения, вид уравнения, граничные условия, примеры.

Наиболее общее волновое уравнение задается как u(x, t) = f (x + ct) + g (x — ct), где f и g – произвольные функции.

Задача обучения

• Вывести решение для волнового уравнения перемежающейся волны.

Основные пункты

• Любая функция u(x, t), подходящая к условию , выступает решением волнового уравнения. Для этого были введены новые переменные φ = x — ct, ψ = x + ct.
• Решения 1D-волнового уравнения – суммы левой и правой движущихся функций.
• Волновая функция также вычисляется путем получения дополнительной информации, обычно заданной граничными условиями.

Термины

• Волновое уравнение – линейной уравнение частных производных второго порядка для описания различных типов волн.
• Граничное условие – набор ограничений на границах, используемых в дифференциальных уравнениях.

Чаще всего, для одномерных волн используют уравнение:

Например, синусоидальная форма u(x, t) = A sin(kx — ωt) выступает решением волнового уравнения для с = ω/k.

Решение волнового уравнения

Отметим, что любая функция u(x, t), подходящая к условию , выступает решением волнового уравнения. Так что обратите внимание на

В середине мы использовали первое уравнение. Теперь вставим новые переменные φ = x — ct, ψ = x + ct и получим:

При смене переменных ∂u+/∂φ = 0 для уравнения со знаком «+» и ∂u-/∂ψ = 0 для знака «-». Поэтому мы видим, что

u₊(φ,ψ) = f(ψ), u_— (φ, ψ) = g(φ), где f и g – произвольные функции. Возвращаясь к исходным переменным x и t, выводим, что решение волнового уравнения:

u (х, t) = f (х + ct) + g (х — ct).

Мы видим, что решение для 1D-волнового уравнения отображает сумму левой (f) и правой (g) перемещающихся волн. Движение означает, что форма их отдельных произвольных функции по х остается стабильной, а вот время и скорость – нет.

Граничное условие

Любая функция с «x + ct» или «x — ct» может выступать решением волнового уравнения. Также можно вычислить при помощи дополнительной информации в виде граничного условия. Например, если речь идет о гитарной струне, то мы знаем, что волна обладает нулевой амплитудой на обоих концах: u (x = 0) = u (x = L) = 0.

Решение волнового уравнения в двух измерения с граничным условием нулевого смещения вдоль всего внешнего края.