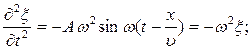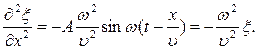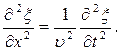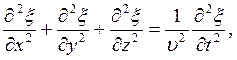Волновое уравнение имеет вид 1 400

Физика волновых процессов

ФИЗИКА ВОЛНОВЫХ ПРОЦЕССОВ

1. Волновое уравнение. Гармонические волны. Уравнение Гельмгольца. Фазовый фронт, фазовая скорость, длина волны. Стоячие волны. Неоднородные плоские волны. Цилиндрические и сферические волны.

2. Плоские электромагнитные волны в поглощающей среде. Глубина проникновения. Поток мощности. Скорость волны. Поверхностный импеданс металлов. Скин-слой.

3. Дисперсия волн. Волновой пакет. Фазовая и групповая скорости. Нормальная и аномальная дисперсии. Дисперсионное уравнение.

4. Прохождение плоской волны через границу раздела двух сред. Коэффициенты Френеля. Явление полного внутреннего отражения. Угол Брюстера. Приближенные граничные условия Леонтовича.

5. Плоские электромагнитные волны в анизотропных средах. Продольное и поперечное распространение в намагниченной плазме. Обыкновенная и необыкновенная волны. Эффекты Фарадея и Коттона-Мутона.

6. Излучение волн. Ближняя и дальняя зоны. Диаграмма направленности линейного излучателя. Понятие области мнимых углов. Излучение волн плоским раскрывом.

7. Электромагнитные волны в направляющих системах. ТЕ, ТМ и ТЕМ волны. Критическая частота. Длина волны в направляющей системе. Волновое сопротивление линии передачи.

8. Приближение геометрической оптики. Уравнение эйконала. Световые лучи. Область применимости лучевого приближения. Принцип Ферма. Рефракция.

Волновое уравнение. Гармонические волны. Уравнение Гельмгольца. Фазовый фронт, фазовая скорость, длина волны. Стоячие волны. Неоднородные плоские волны. Цилиндрические и сферические волны.

Зададим некоторое возмущение, распространяющееся в пространстве, в виде U=U(at–bs), где t – текущее время; s – пространственная координата, вдоль которой распространяется возмущение, и продифференцируем 2 раза по t и 2 раза по s:

(1) (2)

сравнивая (1) и (2) и учитывая, что , где v – скорость распространения возмущения, убеждаемся, что U(s,t) удовлетворяет однородному дифференциальному уравнению в частных производных второго порядка гиперболического типа (уравнению Даламбера), которое принято называть волновым уравнением:

(1-я каноническая форма).

Перейдя к характеристическим переменным , можем записать уравнение в виде (2-я каноническая форма). Эти уравнения описывают распространение возмущения в пространстве в виде свободных волн. Интегрируя последнее уравнение, находим решение в виде суперпозиции двух волн: , первая из которых является уходящей, а вторая – приходящей. Волны, соответствующие решению однородного волнового уравнения, называются свободными волнами.

Здесь предполагается, что U изменяется только в одном направлении s, задаваемом единичным вектором m, тогда s = (mr) (r – радиус-вектор точки наблюдения). В некоторый момент времени t=to U() = const, если s = const. Т. к. (mr) = const – уравнение плоскости, то представляет собой плоскую волну, бегущую в направлении m. Аргумент определяет фазу волны. Плоскость, на которой фаза постоянна (фазовый фронт, поверхность равных фаз) перемещается в пространстве со скоростью v (фазовая скорость).

Если , то функция U может быть представлена в виде интеграла Фурье (образ). Подставив U(s,t) в волновое уравнение, видим что она будет решением, если ее образ F(s,) удовлетворяет уравнению

(приведенное волновое уравнение или уравнение Гельмгольца). Это уравнение описывает распространение гармонических свободных волн. Величина определяет пространственную периодичность функции F и называется волновым числом. Решение уравнения Гельмгольца представляет суперпозицию двух гармонических волн c амплитудами A1, A2 и фазами (wt+j–ks), (wt+y+ks), бегущих навстречу друг другу. Расстояние, которое гармоническая волна пробегает за период колебаний Т, или расстояние между точками с одинаковой фазой колебаний называется длина волны l. Тогда k=. Пусть начальные фазы j и y равны нулю. При А2= 0 имеем уходящую бегущую гармоническую волну , а при А1=0 – приходящую бегущую гармоническую волну . Если А1=А2=А, то , т. е. решение представляет собой синфазное гармоническое колебание, амплитуда которого имеет периодическую пространственную зависимость с периодичностью l/2. Такую ситуацию называют стоячая волна. Точки, в которых F(s) имеет максимум или минимум называют, соответственно, пучностями и узлами стоячей волны. Расстояние между соседними узлами (или пучностями) называется длиной стоячей волны lст = l/2.

Если волна распространяется в направлении единичного вектора m, можем ввести вектор k = km (волновой вектор), тогда ks = (kr), и поверхность равных фаз ks = const определяется уравнением плоскости (kr) = const, нормальной к направлению распространения волны. Если k – вещественный вектор, то А=const всюду. Такая волна называется однородной плоской волной.

Функция F удовлетворяет однородному уравнению Гельмгольца и в том случае, если

k=k+ik но при условии, что |k|2 = k2 – вещественно, т. е. (kk) = 0, а |k|2–|k|2 = k2. В этом случае решение описывает неоднородную плоскую гармоническую волну, у которой поверхность равных фаз и поверхность равных амплитуд – плоскости, ортогональные друг другу, а скорость меньше, чем у однородной волны с той же частотой и в той же среде.

Для произвольной зависимости от координат однородное волновое уравнение имеет следующий вид . Чтобы плоская волна распространялась в направлении оси х (в прямоугольной системе координат), должно выполняться , т. е. источником плоской волны является бесконечная плоскость y0z.

В цилиндрических координатах . Если возмущение исходит от бесконечного цилиндра, то , и волновое уравнение имеет вид . После несложных преобразований его можно привести к виду: . При больших значениях r имеем . Решением этого уравнения является откуда следует, что поверхность равных фаз – цилиндр, а амплитуда волны убывает пропорционально . Такая волна называется цилиндрической.

В сферических координатах . При точечном источнике волновое уравнение можно представить в виде: . Его решение – . В этом случае поверхность равных фаз – сфера, и амплитуда уходящей волны убывает как . Такая волна называется сферической.

1. , , Сухоруков волн. — М.: Наука, 1979.

2. Вайнштейн волны. — М.: Радио и связь, 1988.

Плоские электромагнитные волны в поглощающей среде. Скорость волны. Глубина проникновения. Поверхностный импеданс металлов. Скин-слой. Поток мощности.

В средах с потерями (s ¹ 0) имеем: [ÑH] = iweE+sE = iw (e — is /w)E = iwE, где=—=— is /w = =e (1-itgd), tgd =s /we — тангенс угла электрических потерь. e = e0eотн,; m=m0mотн ;. (eотн=10-9/36p [Ф/м],

mотн= 4p10-7[Гн/м] ). Пусть в такой среде вдоль оси z распространяется плоская гармоническая волна, удовлетворяющая уравнениям: , где волновое число = w оказывается комплексной величиной: =w= b — ia.. Из соотношения w 2m (1–itgd) = (b – ia)2, находим: , . Решение для уходящей волны: Ex=E0 e–a ze–ib z, Hy=e–aze–ib z

Здесь: a – коэффициент затухания, b – коэффициент фазы, Zo – волновое сопротивление среды, , ( 0£d/2

Таким образом, в поглощающей среде амплитуда уходящей волны убывает по экспоненциальному закону,

уменьшаясь в e раз на расстоянии d=1/a, которое называется глубина проникновения (скин-слой), длина волны l=2p/b и фазовая скорость vф=w /b уменьшаются по сравнению с непоглощающей средой, в среде с электрическими потерями Ну отстает по фазе от Еx на величину d /2 (в среде с магнитными потерями, когда комплексной величиной является m , Ну опережает Еx), поверхность равных фаз совпадает с поверхностью равных амплитуд. Для сред с tg d >>1 (металлы) , d®p/2, v =,, ZS= – поверхностный импеданс металла. На границе с хорошо проводящей средой используются приближенные граничные условия: [En] = ZS[n[nH]] — граничные условия Леонтовича.

В среде с потерями поток мощности через единицу поверхности П=[EH*] становится комплексным.

Мгновенное значение Пz равно

Пz=cos(w t-b z)cos(w t-b z —d/2) = [cos2(wt-bz)cos(d/2) + 0.5sin2(w t-b z)sin(d/2)]. Первое слагаемое определяет пульсирующий поток, т. е. мощность, переносимую волной, второе – колеблющийся с удвоенной частотой поток мощности, среднее за период значение которого равно нулю (часть периода поток мощности направлен в обратную сторону). Скорость переноса энергии определяется отношением среднего за период потока мощности к средней плотности энергии vэ = Пср/Wср. В плоской свободной волне запас электрической энергии равен запасу магнитной энергии Wэ = Wм, следовательно Wср= 0,5 Re(Wэ+ Wм) = Re(||e—id +) = ||(cos d+1)=||cos2 (d/2). Пср=0.5Re(e—id/2)= =cos d/2 . Таким образом, vэ = 1/cos (d/2), т. е. при наличии потерь скорость переноса энергии становится меньше.

На рисунке показана временная зависимость вещественной (сплошная линия) и мнимой (пунктирная линия) частей вектора Пойнтинга 1. , , Сухоруков волн. — М.: Наука, 1979. 2. Вайнштейн волны. — М.: Радио и связь, 1988 3. Матвеев .- М.: Высш. школа, 1985. Дисперсия волн. Волновой пакет. Фазовая и групповая скорости. Нормальная и аномальная дисперсии. Дисперсионное уравнение. Плоская гармоническая волна, распространяющаяся вдоль z, имеет вид: E = Eoe– aze– i (bz – wt), где в общем случае a = a(w), b = b(w). Для плоской волны должно быть: wdt –bdz = 0, откуда – фазовая скорость (скорость перемещения фазового фронта). Если b(w), то vф(w), причем может быть vф > c. Означает ли это, что можно передать информацию со скоростью, превышающей скорость света с ? Рассмотрим распространение колебания более сложной формы (сигнал). Пусть в точке z = 0 имеется сигнал f(t) с амплитудным спектром . Каждой составляющей спектра соответствует плоская гармоническая волна, следовательно в точке z > 0 имеем: . Если b=b(w), можем перейти к пространственному спектру, т. е. dw®db, тогда . Выделим вблизи максимума огибающей спектра с частотой wо участок спектра 2Dw = w1 — w2. Пусть Dw vф (vф ω) – аномальная. Если совпадают по направлению – дисперсия положительная, Если имеют противоположные направления – дисперсия отрицательная. Отрицательной аномальной дисперсии быть не может. Если vгр имеет физический смысл, то это скорость переноса энергии. Дисперсионное уравнение. В произвольных линейных средах без искажений может распространяться только плоские гармонические волны, удовлетворяющие уравнению Â(p) = 0, где Â – линейный однородный оператор (для сред, подчиняющихся волновому уравнению Â =). Чтобы гармоническая волна сохраняла форму при любой частоте, необходимо, чтобы в числе решений было решение вида: p = eiw t ± i (kr). Пусть Â переводит р в некоторую функцию q: Â( p) = q. Если qº0, то p – свободная волна в данной среде. Продифференцируем по t, учитывая линейность и однородность Â: , т. е. , где комплексная амплитуда не зависит от t, но может зависеть от w. Подставив p и q в уравнение Â( p) = q, получим уравнение, не зависящее от t, и содержащее w как параметр. Если продифференцировать по координатам, получим: Ñq=ÑÂ(p)=Â(±ikp)= ±ikÂ(p)= ±ikq, т. е. Ñq=±ikq, следовательно, можно представить q в виде: q=f(w,k)eiw t ± i(kr), где f(w,k) кроме w и k может зависеть только от коэффициентов оператора. При произвольных w и k p = eiw t ± i (kr) не свободная волна, т. к. не является решением уравнения Â( p) = 0. Чтобы определить, какие свободные волны могут распространяться (имеют право на существование) в данной среде, необходимо выбрать такие w и k, чтобы . Это уравнение называют дисперсионным уравнением. Каждому значению w соответствует решение этого уравнения относительно k, и каждому k – относительно w. Для изотропной среды это уравнение содержит только |k| и его можно привести к виду – дисперсионное уравнение для данной среды. а) Дисперсионное уравнение, соответствующее волновому уравнению, есть k2 – w2 ¤ c2, где с – const. В этом случае vф = с, ® дисперсии нет. б) Для волн на поверхности воды потенциал скорости удовлетворяет уравнениям Ñ2j = 0, . Ищем волну в виде: j = еiw t – i k x – k z. Получаем дисперсионное уравнение: . Отсюда vф= g /w, т. е. vф зависит от w, следовательно, существует нормальная дисперсия (vф в) Уравнение поперечного смещения стержня при малых колебаниях имеет вид: , где G – коэффициент изгибной жесткости. Ищем решение в виде: еiw t – i k x, получаем дисперсионное уравнение , откуда , т. е. имеется аномальная дисперсия (vф 1. , , Сухоруков волн. — М.: Наука, 1979. 2. Исакович акустика. — М.: Наука, 1978. 4. Прохождение плоской волны через границу раздела двух сред. Коэффициенты Френеля. Явление полного внутреннего отражения. Угол Брюстера. Приближенные граничные условия Леонтовича. Пусть плоская волна из среды с параметрами e1 m1 падает на плоскую границу раздела со средой, имеющей параметры e2 m2. При этом часть мощности отражается, часть проходит во вторую среду, вследствие чего возникают отраженная и преломленная волны. Плоскость, содержащая нормаль к границе раздела и волновой вектор (или вектор Пойнтинга) падающей волны называется плоскость падения. Чтобы определить соотношения между комплексными амплитудами падающей, отраженной и преломленной волн, достаточно рассмотреть два частных случая для линейно поляризованных волн: нормально поляризованная волна (вектор Е нормален к плоскости падения) и параллельно поляризованная волна (вектор Е лежит в плоскости падения). 1. Нормально поляризованная волна q – угол падения, q¢– угол отражения, y – угол преломления. Поле падающей волны: Н1=( yosinq + zocosq)H1, H1= exp[-ik1(-ycosq+zsinq)], компоненты поля отраженной волны: Е¢1х=Еотрexp[-ik1(ycosq¢+zsinq¢)], H¢1= –exp[-k1(ycosq¢+zsinq¢)]. компоненты поля преломленной волны: Е2х=Епрexp[-ik2(ycosy+zsiny)], H2=exp[-ik2(ycosy+zsiny)]. На границе раздела (у = 0) должны выполняться граничные условия: Еt1 = Еt2, Нt1 = Нt2. Для нормально поляризованной волны имеем: Еt1 = Епадexp(-ik1zsinq) + Еотрexp(-ik1zsinq¢), Еt2= Епрexp(-ik2zsiny). Чтобы условие Епадexp(-ik1zsinq) + Еотрexp(-ik1zsinq¢) = Епрexp(-ik2zsiny) выполнялось при любых z, должно выполняться k1sinq = k1sinq¢= k2siny, откуда следует: sinq = sinq¢ и k1sinq = k2siny – законы Снелиуса. Учитывая Нt1= (– )cosq и Ht2= cosy, запишем граничные условия в виде: откуда , , где R^ и T^ – коэффициенты Френеля для нормально поляризованной волны. (R^ – коэффициент отражения, T^ – коэффициент прохождения). Согласно закону сохранения энергии R2^ + T2^= 1. , ,

Компоненты поля в первой и во второй средах имеют вид:

2. Параллельно поляризованная волна

Поле падающей волны:

компоненты поля отраженной волны:

компоненты поля преломленной волны:

Н2х=Нпрexp[-ik2(ycosy+zsiny)], Е2= НпрZ02exp[-ik2(ycosy+zsiny)].

На границе раздела (у=0) для любых z должно выполняться

Нпадexp(-ik1zsinq) + Нотрexp(-ik1zsinq¢) = Нпрexp(-ik2zsiny),

Откуда следуют законы Снелиуса: sinq = sinq¢ и k1sinq = k2siny.

Учитывая Еt1= (НпадZ01+ НотрZ01)cosq и Еt2= НпрZ02cosy, запишем граничные условия для параллельно поляризованной волны в виде:

откуда , ,

где Rêê и Têê – коэффициенты Френеля для параллельно поляризованной волны. (Rêê – коэффициент отражения, Têê – коэффициент прохождения). R2êê + T2êê= 1.

, ,

Компоненты поля в первой и во второй средах имеют вид:

Для диэлектриков m1= m2= m0, и коэффициенты Френеля можно записать в виде:

,

где – показатели преломления первой и второй среды, соответственно.

Анализ этих выражений показывает, что для параллельно поляризованной волны существует угол падения qБ = p/2 – y, при котором R||=0. Этот угол, определяемый из соотношения tgqБ=, называется угол Брюстера или угол полной поляризации, т. к. при падении под углом qБ на границу раздела волны с произвольной поляризацией отраженная волна становится нормально поляризованной, т. е. имеет линейную поляризацию.

Из закона Снелиуса sin y = следует, что в случае n1>n2 (волна надает из более плотной среды) существует критический угол падения qкр, при котором siny =1. Если q >qкр, то siny >1 (это возможно, если y мнимая величина), и cosy = также становится мнимой величиной. В этом случае поле во второй среде имеет характер неоднородной плоской волны (боковой волны), скорость которой меньше скорости света, амплитуда в направлении нормали к границе раздела убывает по закону , т. е. вдали от границы раздела поле отсутствует, энергия переносится вдоль границы. Это явление называется полным внутренним отражением.

При падении волны из свободного пространства на границу раздела с хорошо проводящей средой, у которой tgd>>1, siny Þ 1, т. е. тангенциальные компоненты поля на поверхности проводника непрерывно переходят в поперечные компоненты поля уходящей вглубь проводника волны. Соотношение между ними можно записать в виде Еt=Zos[Htyo], где Zos – поверхностный импеданс проводящей среды, yo – орт нормали к границе раздела. Это импедансное граничное условие называют приближенным граничным условием Леонтовича.

1. , Зернов поля и волны. — М.: Сов. радио, 1971.

2. , Никольская и распространение радиоволн. М. Наука, 1989

Волны в анизотропных средах

Для изотропных сред, свойства которых не зависят от направления, B = mH и D = eE, где e и m — скалярные величины, следовательно: Bx= mHx, By=mHy, Bz=mHz, Dx= eEx, Dy=eEy, Dy=eEy. Существуют анизотропные среды, которые в разных направлениях имеют различные свойства, т. е. связь между проекциями векторов B и H или D и E описывается соотношениями

Bx= mxxHx+ mxyHy + mxzHz, By= myxHx+ myyHy + myzHz, Bz= mzxHx+ mzyHy + mzzHz, .

Dx= exxEx+ exyEy + exzEz, Dy= eyxEx+ eyyEy + eyzEz, Dz= ezxEx+ ezyEy + ezzEz, .

Формально эту связь принято представлять в виде и , где и являются тензорами диэлектрической и магнитной проницаемости, соответственно:

В природе неизвестны вещества, у которых одновременно e и m имеют тензорный характер, поэтому в дальнейшем будем рассматривать вещества, обладающие или диэлектрической или магнитной анизотропией.

Типичными представителями анизотропных сред являются намагниченные плазма и феррит.

Плазма — электрически нейтральный газ, в котором значительная часть атомов или молекул ионизирована

Под действием электрического поля на каждый электрон действует сила Fk= –Eeo (кулоновское взаимодействие). Если движущийся со скоростью v электрон находится в постоянном магнитном поле Н=, на него действует сила Лоренца Fл = –eomo[vH=], вследствие чего электрон получает также вращательное движение. В этом случае уравнение движения электрона имеет вид: , где r – смещение электрона относительно исходного положения, mо и eо – масса и заряд электрона. При смещении электрон приобретает электрический момент p = reo. Пусть H== zoH= и E=Eeiwt. Решение ищем в виде r = reiwt. Если N – концентрация электронов, то электрический момент единицы объема (вектор электрической поляризации) Ре=Nreo. Тогда уравнение движения для единицы объема (без учета столкновения электронов): –w2moPe=NeoE–iweomoH=[Pezo]. Обозначив wm= moeoH=/mo – частота гиромагнитного резонанса (частота вращения электрона) и wo = eo2N ¤ mo eo – критическая частота плазмы, имеем . Учитывая, что D=Pe+eoE, получаем: , где , , . При изменении направления Нz меняется знак b.

Продольное распространение плоской волны в намагниченной плазме

При продольном распространении (вдоль H=) . Решение ищем в виде плоских гармонических волн: Ez=Hz=0, Ex, y=E0x, y e–ikz, Hx, y=e–ikz. Подставляя в уравнения Максвелла [ÑH]=iwE, [ÑE]=–iwmH, имеем систему уравнений:

–ik= –iw(exE0x–ibE0y) , kE0y= wm,. из второй пары уравнений k=wm /Z01, k=wm /Z02.

ik= iw(ibE0x+exE0x), kE0x= wm Подставляя в первую пару, получаем

(k2–w2exmo)E0x= –iw2bmoE0y откуда следует Е0y= iE0x и дисперсионное уравнение:

(k2–w2exmo)E0y= iw2bmoE0x, (k2–w2exmo) = ±w2bmo или k1,2 = w, Z01,2=.

Таким образом, получили два решения, следовательно в намагниченной плазме одновременно распространяются две волны с волновыми числами k1=w и k2=w, имеющие разные волновые сопротивления Z01 = и Z02 =:

Ex1=E01cos(wt–k1z) волна круговой Ex2=E02cos(wt–k2z) волна правого вращения,

Ey1=E01sin(wt–k1z) поляризации левого Ex2=E02sin(wt–k2z) при ex=b, k2 Þ 0, поэтому ее

Hx1= – sin(wt–k1z) вращения H02= sin(wt–k2z) называют необыкновенная волна.

Hy1= –cos(wt–k1z) k1=ko Hy2= cos(wt–k2z) k2=ko

Необыкновенная волна при w Þ wm исчезает вследствие резонансного поглощения (явление гиромагнитного резонанса). Полное поле можно представить в виде: Еx=Ex1+Ex2=2Eocos[0.5(k1–k2)z]cos[wt–0.5(k1–k2)z], Еy=Ey1+Ey2=2Eosin[0.5(k1–k2)z]cos[wt–0.5(k1–k2)z], в каждый момент времени Еx и Еy синфазны, угол наклона вектора Е относительно оси x: q = arctg(Ex/Ey) = 0.5(k1–k2)z, т. е. поле имеет линейную поляризацию, но плоскость поляризации медленно вращается при распространении волны. Это явление называется эффект Фарадея. Угол, на который поворачивается плоскость поляризации при прохождении волной единицы длины q! = 0.5(k1–k2), называется постоянная Фарадея. Среды, в которых наблюдается эффект Фарадея, называются гиротропными (вращающими). Этот эффект невзаимный, т. к. при изменении направления Н= меняет знак b. Поскольку Z01 ¹Z02, поле Н имеет эллиптическую поляризацию.

Поперечное распространение в намагниченной плазме

При поперечном распространении (вдоль оси х) . Тогда уравнения Максвелла имеют вид:

0 = iw(exEx–ibEy) = iwmoHy Ищем решение в виде Ex, y= E0x, yeikx. Подставляя в уравнения

= iw(ibEx+exEy) = iwmoHz Максвелла, получаем две системы уравнений, описывающих

= iwezEz Hx = 0 поведение двух волн:

kH0y = wezE0z дисперсионное уравнение для этой волны: k2 = w2ezmo или . Эта

kE0z = wmoH0y волна «не чувствует» постоянного магнитного поля и называется обыкновенной. Волновое сопротивление обыкновенной волны Zоб=, фазовая скорость – vоб = .

kE0y = wmoH0z Эта волна кроме поперечной имеет продольную составляющую вектора Е, причем

kH0z = w(ibE0x+ exE0y) E0x находится в квадратуре с E0y, т. е. вектор Ен вращается в плоскости x0y.

exE0x = ibE0y Исключая E0x и H0z, получаем дисперсионное уравнение для этой волны: , откуда kн = . Вследствие таких особенностей эта волна называется необыкновенной. Волновое сопротивление для необыкновенной волны Zн=, фазовая скорость – vн = При отсутствии потерь вектор Пойнтинга имеет вещественную продольную составляющую и мнимую поперечную. Учитывая видим, что при w Þwm, ex Þ – ∞, vн Þ 0, т. е. эта волна исчезает (поперечный магнитный резонанс). При поперечном распространении (для w ¹ wm) полное поле H = y0Hоб + z0Hн, E = z0Eоб + Eн. Поскольку и kн ¹ kоб, при поперечном распространении волны периодически меняется вид поляризации. Это явление называется эффект Коттона — — Мутона.

Аналогичные явления имеют место и при распространении волн в намагниченном феррите – веществе, обладающем магнитными свойствами ферромагнетиков (mотн=5¸10000) и электрическими свойствами диэлектриков (eотн=5¸20). В магнитном поле магнитная ось атома прецессирует вокруг направления поля Н=, вследствие чего магнитная проницаемость феррита становится тензором

, где , a = mо. Для получения выражений, описывающих поведение волн в феррите, достаточно воспользоваться принципом двойственности, т. е. в выражениях для плазмы сделать взаимную замену: H Û E, e Û –m.

Литература. , Зернов поля и волны. — М.: Сов. радио, 1971.

Излучение волн. Ближняя и дальняя зоны. Диаграмма направленности линейного излучателя. Понятие области мнимых углов. Излучение волн плоским раскрывом.

Излучение – процесс преобразования энергии источника в энергию свободных волн. Математически задача сводится к решению неоднородного волнового уравнения. В случае электромагнитных волн удобнее использовать векторные потенциалы: Ñ2Ae+ k2Ae = –j ст e, Ñ2Am+ k2Am = –j ст m, где Ae и Am– электрический и магнитный векторные потенциалы, j ст e и j ст m– объемные плотности электрических и магнитных сторонних токов, заданных в объеме Va. Используя метод функции Грина, запишем решение в виде:

, (1)

где – координаты точки наблюдения, – координаты точки источника, r– расстояние от точки источника до точки наблюдения. Для вычисления компонент поля используются соотношения:

Если rо и r¢ радиус-векторы точки наблюдения и точки источника, то , где a –угол между rо и r¢. При rо > r¢, разложив в ряд Тейлора, имеем: r = rо– r¢cosa + (r¢2sin2a)/2ro+( r¢3cosasin2a)/2 r2о+ … .

В зависимости от расстояния до точки наблюдения используются разные приближения:

а) при r >> r¢, дальняя зона (зона Фраунгофера) в показателе экспоненты используется первое приближение: r @ rо– r¢cosa. Минимальное значение rмин, (граница дальней зоны) начиная с которого можно пользоваться этим приближением, определяется из условия (r¢2sin2a)/2ro

выражение (1) имеет вид

.

При вычислении Е и Н по формулам (2) отбрасываются слагаемые, пропорциональные r–2 и r–3. Тогда Еq= – ik(ZоАqе+Аjм), Еj=–ik(ZоАjе+Аqм), Еr=0; Нj= Еq ¤ Zо, Нq= –Еj ¤ Zо, Нr=0; где Zо– волновое сопротивление среды;

Аq=Аxcosq cosj+Аycosq sinj +Аzsinq , Аj= –Аxsinj +Аycosj, Аr=Аxsinq cosj+Аysinq sinj + Аzcosq.

В общем случае поле в дальней зоне можно представить в виде: Е= Еоf(q,j)p(q,j)eiY(q,j). Таким образом, в дальней зоне а) поле поперечно; б) в окрестности точки наблюдения Еq=НjZо, Еj=НqZо, т. е. поле имеет характер плоской волны; в) в общем случае поле имеет эллиптическую поляризацию, которая определяется векторной функцией p(q,j) (поляризационной характеристикой); г) зависимость поля от расстояния , т. е. поле является суперпозицией сферических волн; д) угловое распределение в дальней зоне не зависит от r и определяется функцией f(q,j), которая называется амплитудная диаграмма направленности (зависимость амплитуды поля от направления в дальней зоне при фиксированном расстоянии). Форма диаграммы направленности (ДН) характеризуется направлением максимума qо,jо, шириной главного лепестка (на уровне половинной мощности) Dq0,5, Dj0,5 и уровнем боковых лепестков УБЛ (отношение амплитуд максимально бокового лепестка и главного); е) поток мощности Пr=(|Еq|2+|Еj|2)/2Zо, Im П=0; ж) форма поверхности равных фаз зависит от фазовой диаграммы направленности Y(q,j), и не всегда является сферой с центром в начале координат. Если поверхность равных фаз сфера, то ее центр называется фазовым центром излучателя.

При r l быстрее изменяется fc(q), поэтому рассмотрим зависимость множителя системы от скорости волны тока, определяемой значением b. Введем величину y=kcosq, имеющую смысл пространственной частоты (–¥ k, называется областью мнимых углов, т. к. при этом cosq>1. Видно, что уменьшение скорости волны тока приводит к смещению максимума ДН от нормали к оси излучателя. Если скорость волны тока меньше скорости света (b>k), большая часть энергии “излучается” в область мнимых углов, т. е. отсутствует в дальней зоне и находится вблизи излучателя.

Для синфазного излучателя Dq0,5=51оl / L, УБЛ=0.21.

Излучение волн плоским раскрывом (апертурой)

Пусть на прямоугольной площадке, расположенной в плоскости x,y задано распределение поверхностных токов Je, m(x¢, y¢). В дальней зоне , где u = ksinqcosj, v = ksinqsinj, S = a×b – площадь раскрыва. Тогда Eq= –ik(ZoAeycosqsinj – Amxsinj) = ,

Ej= –ik(ZoAeycosj– Amx cosqcosj)= . Если источником излучения

является поверхность с заданным на ней распределением электромагнитного поля, например раскрыв рупорной антенны, то согласно принципу эквивалентных токов Je=[Hn], Jm= – [En]. В этом случае Jmx= Eаy, Jey= – Hаx= – Eаy/Zф (здесь Zф= Eаy/Hаx – сопротивление фронта волны, возбуждающей раскрыв) и выражения для полей имеют вид:

Таким образом, излученное поле является суперпозицией сферических волн, имеет в общем случае эллиптическую поляризацию и диаграмма направленности излучателя может быть представлена в виде произведения множителя элемента на множитель системы: f(q, j) = fэ (q, j)fc(q, j), где fэ (q) = при j = 0, и fэ (q) = при j = 90о, т. е. при Zф @ Z0 ДН элемента излучающей поверхности имеет форму кардиоиды. Если Eаy(x¢,y¢) = Eа1y(x¢)×Eа2y(y¢), то множитель системы fc(q, j) = = , и при равномерном синфазном распределении поля в раскрыве fc(q, j) = .

Литература

1. , , Грудинская и распространение радио­волн. — М.:Сов. радио,1979.

Электромагнитные волны в направляющих системах. ТЕ, ТМ и ТЕМ волны. Критическая частота. Длина волны в направляющей системе. Волновое сопротивление линии передачи.

Плоские однородные волны – простейший тип волнового процесса. При наличии границ возникают неоднородные плоские волны, распространяющиеся вдоль этих границ, т. е. возникают плоские направляемые волны. Это делает возможным передачу энергии на большие расстояния с минимальными потерями. Варианты конструктивного исполнения направляющих систем (линий передачи) приведены на рисунке.

Будем считать эти системы продольно однородными (их свойства сохраняются в одном прямолинейном направлении, например, вдоль оси z). Свободные плоские гармонические волны, способные распространяться в направляющей системе, определяются из однородных уравнений Гельмгольца: Ñ2Е + k2E = 0, Ñ2H + k2H = 0. В отличие от плоской волны в неограниченном пространстве, в направляющих системах могут существовать неоднородные плоские волны, имеющие продольную составляющую поля Еz или Нz. Связь между продольными и поперечными составляющими поля определим, используя метод разделения переменных, т. е. полагая Е = Е^(x,y)×exp(±igz), H = H^(x,y)×exp(±igz). Здесь g – продольное волновое число, определяющее скорость распространения волны вдоль z. Для поперечных компонент поля имеем Ñ2Е^+ (k2– g2) E^= 0, Ñ2Н^+ (k2– g2) Н^= 0, где (k2– g2) = c2 – поперечное волновое число, k2 = w2em, e и m – параметры среды, заполняющей линию передачи. Используя координатную запись однородных уравнений Максвелла относительно комплексных амплитуд Е и Н, имеем:

rot H = iweE + igHy = iweEx igEx+ = iwmHy решая относительно Еx и Нy, а затем

rot E = –iwmH + igEy = –iwmHx igHx + = – iweEy относительно Еy и Нx, получаем систему уравнений, связывающих поперечные и продольные составляющие поля:

полагая E┴ = xoEx+ yoEy и H┴ = xoHx+ yoHy ,

в векторной форме имеем:

, т. о., для нахождения структуры поля достаточно решить Ñ2Еz+ c2 Ez = 0 и Ñ2Hz+ c2 Hz = 0. В зависимости от структуры поля направляемые волны делятся на

поперечные – ТЕМ или Т волны (отсутствуют продольные составляющие поля),

электрические – ТМ или Е волны (имеется продольная составляющая электрического поля),

магнитные – ТЕ или Н волны (имеется продольная составляющая магнитного поля),

гибридные – ЕН волны (имеется продольные составляющие электрического и магнитного поля).

Критическая частота: для волн Е и Н типа из c2 = (k2– g2) следует, что является вещественной величиной, если c £ k, в этом случае Е

exp(–igz), т. е. амплитуда волны, распространяющейся вдоль z остается постоянной и меняется только фаза. Если c > k, то g – мнимая величина, следовательно, постоянной остается фаза и по экспоненте убывает амплитуда. При g= 0 имеем: c = k = 2pfкр , где fкр= c /2p – критическая частота, которой соответствует критическая длина волны lкр=2p/c. Таким образом, длина волны в направляющей системе , фазовая скорость vф = , и передача энергии по волноводным линиям (трубам) возможна только при f >fкр.

Для ТЕМ волн (Еz =0 и Нz = 0) c2= 0, следовательно, g = k и fкр= 0, т. е. передача энергии возможна на всех частотах, включая нулевую (постоянный ток).

Волновое сопротивление линий передачи определяется исходя из следующих соображений:

используя систему уравнений, связывающих продольные и поперечные составляющие поля, получаем

для Е(ТМ) волн (Нz=0): , , откуда , т. е. , где Z0= – волновое сопротивление среды, заполняющей линию передачи.

Для Н(ТЕ) волн (Еz=0): , , откуда , т. е.

. Для ТЕМ волн (Нz=Еz=0, g=k) имеем: , откуда . Поскольку ТЕМ волны могут существовать только в двухпроводных линиях, если расстояние между проводниками > 2(ÑA)( ÑL) ® koAn >>(ÑA) (т. к. |ÑL| = n), или || > Ñ2L ® 2-я производная связана с кривизной ПРФ. Для плоской кривой L=f(x) радиус кривизны

, полагая , имеем , т. е. радиус кривизны волнового фронта должен быть>>l. С другой стороны, |Ñ2L|=|Ñ(ÑL)|=|Ñn|, т. е. , следовательно

изменение n на длине волны должно быть > Ñ2A – это условие связано с кривизной поверхности равных амплитуд rА и может быть записано в виде 2pnrA/l >>l/2pnA2, т. е. радиус кривизны ПРА, отнесенный к l, должен быть >> l. Чтобы пренебречь дифракционными явлениями размер фронта волны D должен быть >> l/n. Эти условия не выполняются в точках, где пересекаются лучи (фокус оптических систем); в средах с резкими неоднородностями; в мутных средах; при прохождении поверхностей с поглощающими экранами и т. д.

В неоднородной среде луч, соединяющий две точки р1 и р2, является кривой линией. Для каждой точки луча имеем: dL= (grad L×dr)=| grad L||dr|=k0n(r)dl, где dr направлен по лучу, dl – элемент длины пути. Изменение фазы вдоль луча равно . Принцип Ферма утверждает, что интеграл вдоль луча имеет стационарное значение, т. е. первая вариация dL относительно соседних путей интегрирования равна нулю. Учитывая, что dl/v = dt и n(r)=c/v(r), где dt – время прохождения пути dl со скоростью v, с – скорость света в вакууме, имеем =, где интеграл дает время, затрачиваемое светом на прохождение пути от р1 до р2. Это позволяет сформулировать принцип Ферма следующим образом: лучом, соединяющим две точки является тот путь, который делает стационарным время, затрачиваемое на его прохождение. Ферма в 1657г. сформулировал его следующим образом «Природа всегда следует наикратчайшему пути». Однако таких путей может быть много, например, оптические длины всех путей, соединяющих точку предмета с точкой изображения, одинаковы (принцип таутохронизма).

В однородной среде луч – прямая линия. При переходе границы раздела между двумя различными средами луч меняет направление. Соединим лучом точку р1(0,у1) в среде с показателем преломления n1 с точкой р2(а,у2) в среде с показателем преломления n2. Луч пересекает границу раздела в точке (х,0). Полное время распространения света от р1 до р2 равно t = . Используя условие стационарности , получаем: . Учитывая, что , , где q – угол между направлением луча и нормалью к границе раздела, имеем: n1sinq1 = n2sinq2 – закон преломления.

В плоскослоистой среде луч искривляется. Это явление называется рефракция. Радиус кривизны луча r для плоскослоистой среды определяется следующим образом: согласно рисунку r=ab/dq. Из закона преломления имеем: nsinq= =(n+dn)sin(q+dq) »nsinq +ncosq dq +sinq dh. Отсюда ncosq dq = = – sinqdh. Из подобия треугольников abc и Оab находим . Таким образом, .

Для нормального состояния атмосферы и радиус кривизны луча в радиодиапазоне rрад»25000км, в оптическом диапазоне – rоп»50000км. При расчете радиотрасс считается, что луч распространяется по прямой, q=90о, но радиус Земли принимается равным , где аз – радиус Земли, равный 6370 км. Для нормальной атмосферы и аэкв= 8500 км, т. е. расстояние прямой видимости увеличивается приблизительно на 15%.

В зависимости от состояния атмосферы различают следующие типы рефракции:

а) – отрицательная (луч отклоняется от Земли), аэкв аз.

г) – критическая (луч параллелен поверхности Земли), аэквÞ ¥.

д) – сверхкритическая ( луч возвращается к Земле), аэкв

Волновое уравнение

Вы будете перенаправлены на Автор24

В том случае если волна распространяется в однородной среде, то ее движение в общем случае описывают волновым уравнением (дифференциальным уравнением в частных производных):

где $v$ — фазовая скорость волны $\triangle =\frac<<\partial >^2><\partial x^2>+\frac<<\partial >^2><\partial y^2>+\frac<<\partial >^2><\partial z^2>$ — оператор Лапласа. Решением уравнения (1,2) служит уравнение любой волны, данные уравнения удовлетворяют, например, и плоская и сферическая волны.

Если плоская волна распространяется вдоль оси $X$, то уравнение (1) представляется как:

Если физическая величина распространяется как волна, то она обязательно удовлетворяет волновому уравнению. Справедливо обратное утверждение: если какая — либо величина подчиняется волновому уравнению, то она распространяется как волна. Скорость распространения волны будет равна квадратному корню из коэффициента, который стоит при сумме пространственных производных (в данном виде записи).

Волновое уравнение играет очень большую роль в физике.

Решение волнового уравнения для плоской волны

Запишем общее решение уравнения (2), для световой волны, распространяющейся в вакууме в случае, если s скалярная функция зависит только от одной из декартовых переменных, например $z$, то есть $s=s(z,t)$, что означает, функция $s$ имеет постоянное значение в точках плоскости, которая перпендикулярна $оси Z$. Волновое уравнение (1) в этом случае примет вид:

Готовые работы на аналогичную тему

где скорость распространения света в вакууме равна $c$.

Общим решением уравнения (4) при заданных условиях будет выражение:

где $s_1\left(z+ct\right)$- функция описывающая волну произвольной формы, которая перемещается со скоростью $c$ в отрицательном направлении по отношению к направлению $оси Z$, $s_2\left(z-ct\right)$ — функция описывающая волну произвольной формы, которая перемещается со скоростью $c$ в положительном направлении по отношению к направлению $оси Z$. Надо отметить, что в процессе движения значения $s_1$ и $s_2$ в любой точке волны и ее форма волны неизменны.

Получается, что волна, которую описывает суперпозиция двух волн (в соответствии с формулой (5)). Причем эти составляющие волны движутся в противоположных направлениях. В этом случае уже нельзя говорить о скорости или направлении волны. В самом простом случае получается стоячая волна. В общем случае необходимо рассматривать сложное электромагнитное поле.

Волновое уравнение и система уравнений Максвелла

Волновые уравнения для колебаний векторов напряженности электрического поля и вектора магнитной индукции магнитного поля легко получить из системы уравнений Максвелла в дифференциальной форме. Запишем систему уравнений Максвелла для вещества, в котором нет свободных зарядов и токов проводимости:

Применим операцию $rot$ к уравнению (7):

В выражении (10) можно изменить порядок дифференцирования в правой части выражения, так как пространственные координаты и время — независимые переменные, следовательно, имеем:

Примем во внимание то, уравнение (6), заменим $rot\overrightarrow$ в выражении (11) на правую часть формулы (6), имеем:

Зная, что $rotrot\overrightarrow=graddiv\overrightarrow—<\nabla >^2\overrightarrow$, и используя $div\overrightarrow=0$, получаем:

Аналогично можно получить волновое уравнение для вектора магнитной индукции. Оно имеет вид:

В выражениях (13) и (14) фазовая скорость распространения волны $(v)$ равна:

Задание: Получите общее решение волнового уравнения $\frac<<\partial >^2s><\partial z^2>-\frac<1>\frac<<\partial >^2s><\partial t^2>=0(1.1)$ плоской световой волны.

Решение:

Введем независимые переменные вида для функции $s$:

\[\xi =z-ct,\ \eta =z+ct\left(1.2\right).\]

В таком случае частная производная $\frac<\partial s><\partial z>$ равна:

Частная производная $\frac<\partial s><\partial t>$ равна:

Вычтем почленно выражение (1.4) из выражения (1.3), имеем:

Почленное сложение выражений (1.4) и (1.3) дает:

Найдем произведение левых частей выражений (1.5) и (1.6) и учтем результаты, записанные в правых частях этих выражений:

Если проинтегрировать выражение (1.7) по $\xi $, то получим функцию, которая не зависит от этой переменной, и может зависеть только от $\eta $, что значит, что она является произвольной функцией $\Psi(\eta )$. В этом случае уравнение (1.7) примет вид:

Проведем интегрирование (1.8) по $\eta $ имеем:

где $s_1\left(з\right)$ — первообразная, $s_2\left(\xi \right)$- постоянная интегрирования. Причем, функции $s_1$ и $s_2$ — произвольные. Учитывая выражения (1.2), общее решение уравнения (1.1) можно записать как:

Ответ: $s\left(z,t\right)=s_1\left(z+ct\right)+s_2\left(z-ct\right).$

Задание: Определите из волнового уравнения, чему равна фазовая скорость распространения плоской световой волны.

Решение:

Сравнивая волновое уравнение, например, для вектора напряженности, полученное из уравнений Максвелла:

с волновым уравнением:

позволяет сделать вывод о том, что скорость распространения волны $(v)$ равна:

Но здесь требуется отметить, что понятие скорости электромагнитной волны имеет определенный смысл только с волнами простой конфигурации, под такие волны подходит, например категория плоских волн. Так $v$ не будет являться скоростью распространения волны в случае производного решения волнового уравнения, в состав которых входят, например, стоячие волны.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 26 02 2021

Уравнение бегущей волны. Волновое уравнение

Лекция 6. Механические волновые процессы

План лекции

6.1. Возникновение волны. Продольные и поперечные волны.

6.2. Уравнение бегущей волны. Волновое уравнение.

6.3. Фазовая и групповая скорости.

6.4. Волны в упругих средах.

6.5. Звук и его характеристики.

6.6. Элементы акустики и их значение в строительстве.

6.7. Использование энергии упругих волн в строительстве.

Возникновение волны. Продольные и поперечные волны

Если в среде колеблется частица, то она приводит в колебание соседние частицы. Процесс распространения колебаний называется волной. Направление распространения колебаний называется лучом. В зависимости от направления колебаний частиц относительно луча различают волны продольные и поперечные. Если колебания происходят вдоль луча, то волна продольная, а если колебания перпендикулярны лучу — волна поперечная. Продольные волны распространяются в средах, в которых возникают упругие силы при деформациях растяжения – сжатия (разрежения – уплотнения), то есть в твердых, жидких и газообразных телах. Поперечные волны распространяются в средах, в которых возникают упругие силы при деформациях сдвига, т.е. в твердых телах. Таким образом в жидкостях и газах возникают только продольные волны, а в твердых телах – как продольные, так и поперечные.

Поверхность, до которой дошли колебания частиц к моменту времени t, называется фронтом волны. Совокупность точек (частиц), колеблющихся в одинаковых фазах, образует волновую поверхность. Если фронт волны плоский, волна называется плоской. Если фронт волны представляет собой поверхность шара, волна называется сферической. Так волна, распространяющаяся от точечного источника в однородной среде, будет сферической.

При волновом процессе точка среды совершает колебания относительно положения равновесия и почти не имеет поступательного перемещения вдоль луча. От источника поступательно перемещаются фаза и энергия колебаний. Соответственно скорость перемещения фазы – фазовая скорость, перенос энергии – групповая скорость.

Уравнение бегущей волны. Волновое уравнение

Уравнение бегущей волны выражает зависимость смещения колеблющейся частицы от координаты и времени.

Рассмотрим вывод уравнения плоской синусоидальной волны. Пусть упругая волна распространяется вдоль оси x. Если ξ(x,t)= Asinωt будет уравнением колебания точки (частицы), то такие же колебания частицы, отстоящей от источника на расстоянии x, произойдут позже, то есть с опозданием на время x/υ. Точка (частица) на расстоянии x будет иметь такое смещение в момент времени t , как и начальная точка в момент (t -x/υ). Тогда уравнение колебаний частиц, колеблющихся в плоскости XOY, или уравнение плоской бегущей волны будет:

Если фазовая скорость имеет обратное направление (-υ), то есть волна распространяется в обратном направлении, то

Без учета поглощения энергии в общем случае уравнение плоской синусоидальной волны, распространяющейся вдоль положительного направления оси OX, будет:

где A — амплитуда волны,

φ₀— начальная фаза колебаний, определяемая выбором начала отсчета x и t ;

[ω(t ± x/υ) + φ₀] — фаза плоской волны.

Введем в уравнения (6.1) и (6.2) волновое число:

(6.3)

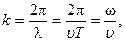
где λ — длина волны;

T — период колебаний;

ω — циклическая частота.

Обобщив (6.1), (6.2) и (6.3), перепишем уравнение плоской бегущей волны в виде:

Направление волны зависит от знака (+) или (-) перед kx.. .

Аналогично можно показать, что уравнение сферической синусоидальной волны (её волновые поверхности имеют вид концентрических сфер) записывается так:

ξ(r,t) = 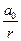sin(ωt ± kr + φ₀), (6.5)

где 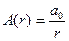— амплитуда волны,

a₀ — физическая величина, численно равная амплитуде на единичном расстоянии от центра волны.

Из (6.5) видно, что амплитуда колебаний сферической синусоидальной волны не остается постоянной, а убывает с расстоянием r от источника по закону 1/r .

Существуют и другие формы записи синусоидальной плоской и сферической волны 1 .

1 Основываясь на формуле Эйлера, уравнения этих волн в экспоненциальной форме можно записать так:

— плоская волна;

— сферическая волна.

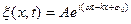
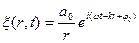
Уравнение волны (6.4) – одно из возможных решений общего дифференциального уравнения с частными производными, описывающее процесс распространения возмущения в среде. Такое уравнение называется волновым. Его можно получить продифференцировав (6.4) по два раза, сначала по t, а затем по x:

Сравнивая эти уравнения получим волновое уравнение для плоской волны, распространяющейся вдоль оси OX:

Волновое уравнение в общем случае:

— оператор Лапласа.

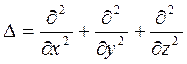
Дата добавления: 2015-10-26 ; просмотров: 4014 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ