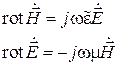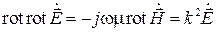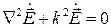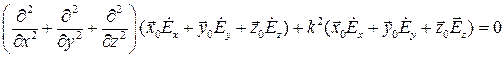Волновой характер электромагнитного поля уравнения гельмгольца

Уравнения Гельмгольца. Волновой характер электромагнитного поля

Одним из важнейших результатов, полученных Максвеллом, явилось доказательство волновой природы электромагнитного поля. Уже упоминалось о том, что изменение во времени электрического поля приводит к возникновению магнитного поля, неоднородного в пространстве, и наоборот. Физическая картина здесь напоминает процесс обмена энергией между электрическим и магнитным полем в обычном колебательном контуре. Поэтому можно ожидать, что электромагнитный процесс в самом общем случае представляет собой также некоторые колебания. Принципиальная разница здесь заключается в том, что колебания электромагнитного поля должны рассматриваться одновременно во всех точках пространства. В физике колебательное движение непрерывной среды принято называть волновым процессом.

Докажем волновой характер электромагнитного поля математически, сведя уравнения Максвелла к другим уравнениям, которые заведомо описывают волновой процесс.

Рассмотрим электромагнитное поле в некоторой области пространства, где плотность зарядов отсутствует, т.е. 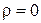. Плотность сторонних электрических токов также предполагается равной нулю.

Выпишем первые два уравнения из общей системы уравнений Максвелла для комплексных амплитуд в виде:

Эти два уравнения могут быть сведены к одному. Для этого применим операцию rot к левой и правой частям второго уравнения, а затем выразим полученную правую часть через второе уравнение:

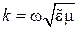
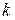
Здесь − в общем случае комплексное число, являющееся, как будет показано, постоянной распространения электромагнитной волны. В литературе для величины можно встретить также названия фазовая постоянная или волновое число.

Дальнейшее преобразование формулы можно осуществить, если воспользоваться известным тождеством векторного анализа:

.

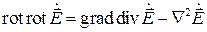
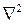
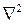
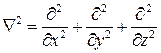
Здесь (набла квадрат) − векторный дифференциальный оператор второго порядка, конкретная форма которого полностью определяется той координатной системой, в которой производятся вычисления. Для декартовой системы координат действие оператора сводится к тому, что к каждой из проекций векторного поля применяется оператор Лапласа

.

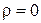
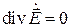
Если воспользоваться законом Гаусса, который в соответствии с принятым условием обеспечивает , то уравнение может быть переписано в следующем простом виде:

Пользуясь симметрией уравнений Максвелла, совершенно аналогично получаем также уравнение относительно векторного поля :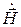

.

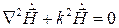
Эти два уравнения в математической физике носят название уравнений Гельмгольца. Математически можно показать, что эти уравнения описывают стационарные волновые процессы, т.е., распространение в пространстве волн с некоторой постоянной частотой.

Таким образом, получен фундаментальный вывод теории Максвелла − переменность во времени электрических или магнитных полей приводит к распространению в пространстве электромагнитных волн.

В координатной форме уравнения Гельмгольца записываются следующим образом

.

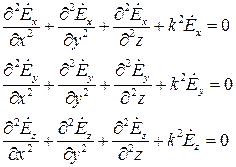
Решение такой системы значительно упрощается в тех частных случаях, когда поле не имеет каких-либо составляющих, например, 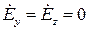, а также тогда, когда поле постоянно в каких-либо плоскостях, например .

Дата добавления: 2015-10-19 ; просмотров: 1856 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Лекция №6 Волновой характер электромагнитного поля

Тема №2 РАСПРОСТРАНЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН Лекция №6 Волновой характер электромагнитного поля Учебные вопросы: 1.

Уравнения Гельмгольца 2.

Однородная плоская волна в среде без потерь.

Однородная плоская волна в среде с потерями 1.

• Максвелл получил один из важнейших результатов электродинамики, доказав, что распространение электромагнитных процессов в пространстве с течением времени происходит в виде волны.

• существует некоторый объем с ρ=0.

• На этот объем не действуют сторонние силы.

• Сигнал, заключенный в этот объем, гармонический. ωµ−= ωε=•.,HjErotEjHrota•→•→•→•→•→=−=−=−=EjEjHrotjE rotrotaεµωεµω ωε ωµ2)(aεµω=γ2•→•→•→γ=εµω=E rotrota2•→•→•→∇−=E graddivE rotrot2 Обозначим -постоянная распространения в среде На основе известного тождества в векторном анализе можно записать:αβγ⋅−=j2zyx∂+∂+∂=∇ Оператор Лапласа в декартовой системе координат0=ερ=•→Ediv•→•→ −∇=γE202=γ+∇•→•→E02=+∇•→•→Hγ или Учитывая закон Гаусса Пользуясь симметрией уравнений Максвелла Уравнения вида

• называются уравнениями Гельмгольца.02=γ+∇•→•→E02=+∇•→•→Hγ0202=+⋅γ++⋅∇∂+∂+∂→zEyExEzEyExEzyxzyxzyx   =⋅+∂+∂+∂=⋅+∂+∂+∂=⋅+∂+∂+∂02zyxEzEyExEzEyExEzEyExE γ В декартовой системе координат уравнение Гельмгольца записываются в виде:

• Такими функциями являются векторный и скалярный электродинамические потенциалы .À.0,.=⋅−=+⋅=•BdivDdivBjErotJEjHrot ñòàρωεω В сложных задачах, когда необходимо определить ЭМП в области, содержащей сторонние токи и заряда, вводятся некоторые вспомогательные функции.ϕArotB=→ArotHaµ1=,Aj gradE⋅ω⋅−ϕ−=,ϕ−= gradE Неоднородное волновое уравнение для векторного электродинамического потенциала имеет вид:

• Неоднородное уравнение для скалярного электродинамического потенциала может быть представлено в виде:

• Полученные неоднородные уравнения для векторного и скалярного электродинамических потенциалов имеют решения в виде:

• гдеМ – произвольная точка М, — объемная плотность заряда,γ – постоянная распространения,r – текущее расстояние от каждого элемента объема источника до точки М..2 ñòaJA⋅µ−=γ+∇.2a ñòερϕγϕ−=+∇()dVreMVar ñòM∫⋅=⋅−επρϕγ4 (),4.dVreJMAVr ñòa∫⋅πµ=⋅γ− Решение для электродинамических потенциалов называется интегралом Кирхгофа для запаздывающих потенциалов.

• Очевидно, что элементарный потенциал определяется в момент времени ,

• Значение времени запаздывания определяется:dVrådVråetdartatr⋅=⋅=⋅−⋅−επρεπρϕωγωγ4)()( ôVrt−.ωγrVrtôç⋅=: Вывод: Вывод

• Переменные во времени электрическое и магнитное поле неизбежно приводит к распространению в пространстве электромагнитных волн..γω=V Т.к.

скорость распространения волны является конечной величиной, то воздействие источника, порождающего волны, до произвольной точки М доходит с запаздыванием во времени..ω⋅γ=rVrtç 2.Однородная плоская волна в среде без потерь.

• Рассмотрим однородную плоскую волну в среде без потерь.

Векторы и однородной плоской волны удовлетворяют уравнениям Максвелла без сторонних источников.02=+•óHäzHäβ02=+∂xEzE βzjzjxeBeAEβ0 +=−)(10zjzjcyeBeAZHβ −=−αβγ⋅−=jacZεµ= — характеристическое сопротивление среды.

Электромагнитное поле представляет собой суперпозицию четырех не зависящих друг от друга бегущих волн, имеющих амплитуды .

ВекторыE иH волны лежат в волновых плоскостях и представляют собой поперечные составляющие векторов поля по отношению к направлению распространения.

Электромагнитную волну, имеющую только поперечные составляющие векторовE иH, называют поперечной электромагнитной волной) cos(),(ztÅtzÅmõβω⋅=) cos(),(ztHtzHmóβω⋅=fπ=ω2λπ=β2- Коэффициент фазы показывает на сколько меняется фаза волны на единице длины, часто его называют волновым числом.- — круговая частота Плотность потока мощности волны характеризует вектор Пойнтинга[])(cos20kztZAzHEÏcm−=×=ω 0zHZEc×= ,[]EzZHc×=01 Векторы волны лежат в плоскости фазового фронта.

Они перпендикулярны друг другу и образуют с направлением движения волны правую тройку векторов:acZεµ= — характеристическое сопротивление среды.

Уравнение фазового фронта имеет вид:

• Фазовой скоростью волны Vф называется скорость движения волны

• Геометрическое место точек, колеблящихся с одинаковой фазой, называется волновой поверхностью.

• — длина волныaôVµεβω1= constzta=+−ϕβωôTVfV=λxS1λ∆x2 Уравнение сферической волны:) cos(),(0rtrAtrAβ−ω⋅= Уравнение цилиндрической волн:) cos(),(0rtrAtrAβ−ω⋅= В однородной плоской волне плотности энергии электрического и магнитного полей одинаковы в любой точке в любой момент времени Свойства плоской однородной волны в среде без потерь:

• Амплитуды поля в процессе распространения не меняется.

• Электрическое и магнитное поля синфазны .

• Фазовая скорость не зависит от частоты.

• Электрическая и магнитная объемные плотности энергии в любой момент времени равны.

• Фазовая скорость совпадает со скоростью движения энергии.2HEwameµ+ε=+=.

• Однородные плоские электромагнитные волны являются поперечными и векторы и перпендикулярны друг другу.

• Напряженности электрического и магнитного полей связаны друг с другом так, что плотности энергии электрического и магнитного полей одинаковы в любой точке пространства.

• Для монохроматической волны установлено, что колебания напряженностейЕ иН происходят синфазно.

Однородная плоская волна в среде с потерями

• Среда с электрическими потерями характеризуется конечной величиной удельной проводимости .

Распространить полученные выше результаты на среду с потерями можно, если в соответствующих формулах для среды без потерь заменить абсолютную диэлектрическую проницаемость комплексной диэлектрической проницаемостью:()δεjtga−=1

σatg ωεσ=δ – тангенс угла диэлектрических потерь.

При такой замене коэффициент фазы переходит в комплексный коэффициент распространения , который представляют в виде суммы вещественной и мнимой частей:γα−β=γj)1(

δµεωµεωγjtga−= Мнимая частью коэффициента распространения, которая характеризует быстроту уменьшения амплитуды, поэтому ее называют коэффициентом затухания.

Единицей измеренияα является 1/м.)1(2−δ+µεω=αtga)1(2+δ+µεω=βtgazjzjxeBeAEβ0 +=− Коэффициент фазы определяет изменение фазы векторов поля в направлении распространения.

Коэффициент фазы измеряют в радианах на метр (рад/м).)(10zjzjcyeBeAZHβ −=− Характеристическое сопротивление среды с потерями является комплексной величиной:ψ=δ−εµ=εµ=icaceZjtgZ)1(2)(21δ=δ=ψtg arctg Перейдя от комплексных амплитуд в к мгновенным значениям, получим:) cos()(0azmxzteÅxtEϕβωα+−=−)2/ cos()(0δϕβωα−+−=−azcmyzteZÅytHδ+εµ=21tgZac Амплитуды векторов поля уменьшаются ве = 2,718 раз при прохождении волной расстояния d = 1/α .

Это расстояние называют глубиной проникновения поля в среду, или толщиной скин-слоя.zmeÅzEα−=)(zcmeZÅzHα−=)( В среде с потерями ЭМВ характеризуются следующими свойствами:1).

Электрическая и магнитная составляющие ЭМП в среде с потерями взаимно ортогональны друг другу и направлению распространения.

В среде с потерями амплитуды векторов поля однородной плоской волны затухают в направлении распространения по экспоненциальному закону:2).

В среде с потерями взаимно перпендикулярные векторыE иH однородной плоской бегущей волны сдвинуты друг относительно друга по фазе на величину аргумента комплексного характеристического сопротивления и отличаются по амплитуде в раз.•3).

Формула для фазовой скорости имеет вид:

• Поскольку зависит отω то фазовая скорость зависит как от параметров среды, так и от частоты колебаний.

Явление зависимости фазовой скорости от частоты называют дисперсией электромагнитных волн.zcmeZÅzHα−=)(ψ=δ−εµ=εµ=icaceZjtgZ)1(cZ2)(21δ=δ=ψtg arctg)1(212+δ+µε=βω=tgVaôatg ωεσ=δ 4).

Длины волны в среде с потерями зависит от параметров среды

• Согласно определению длины волны

Распространение волны сопровождается переносом энергии.

Комплексный вектор Пойнтинга означает, что существует активный и реактивный поток мощности

• Среднее значение вектора Пойнтинга)1(212+δ+µε=βπ=λtgfa2