Волны в физике — виды, формулы и определения с примерами
Содержание:
Волны:
Стоя на берегу озера или пруда, вы могли наблюдать, как кольцами разбегаются волны от места, куда был брошен камень, как волны раскачивают лодку или катер. Ветер нарушает равновесие морской поверхности, кажется, что море надвигается на берег, но это не так. Не перемещаются по полю колосья, когда «волнуется» нива, они только наклоняются и опять выпрямляются. Вслед за кораблем или лодкой всегда возникает типичная картина волн.
Волновые процессы широко распространены в природе. Физические основы волновых движений различны, но все они объясняются одинаковыми законами.
Что же такое волна и каковы причины возникновения волн
Вам известно, что твердые, жидкие и газообразные тела состоят из частей, взаимодействующих между собой. Если частица тела начинает совершать колебания, то в результате взаимодействия ее с другими частицами тела это движение распространяется с определенной скоростью во всех направлениях.
Волна — процесс распространения колебаний в любой среде. Волна — это изменение состояния среды, распространяющееся в пространстве и переносящее энергию.
Наблюдения. Рассмотрим особенности распространения волн. Если рассматривать волны на поверхности воды (рис. 204), то они кажутся валами, движущимися в определенном направлении, причем расстояния между валами, или гребнями, одинаковы.
Если бросить в воду поплавок, его не будет относить волной, а он начнет совершать колебания вверх-вниз, оставаясь почти на одном месте.
При распространении волны изменяется состояние колеблющейся среды, но не перенос вещества. От брошенного камня начинает колебаться определенный участок воды, эти колебания передаются соседним участкам и постепенно распространяются во все стороны. Течение воды не возникает, перемещается только форма ее поверхности.
Опыт 1. Закрепим один конец длинного резинового шнура и легонько заставим шнур колебаться. По шнуру побежит волна (рис. 205). Чем сильнее колеблется шнур, тем больше скорость распространения волны. Волна добежит до точки крепежа, отразится и побежит в обратном направлении.
При распространении волны изменяется только форма шнура, а каждый его участок колеблется относительно своего положения равновесия, причем колебания происходят в направлении, перпендикулярном направлению распространения волны (рис. 206). Такие волны называют поперечными волнами.
Поперечные волны
Поперечные волны — это волны, в которых частицы совершают колебания в направлении, перпендикулярном направлению распространения волны.
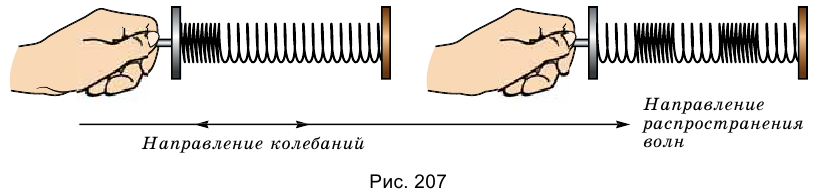
Опыт 2. Если ударить по одному из концов длинной мягкой пружины большого диаметра, то по пружине «побежит» сжатие. Повторяя удары, можно возбудить в пружине волну, представляющую собой последовательные сжатия и растяжения пружины, «бегущие» друг за другом (рис. 207). Любой виток пружины совершает колебания вдоль направления распространения волны. Такую волну называют продольной волной.
Продольные волны
Продольные волны — это волны, в которых частицы совершают колебания вдоль направления распространения волны.
При распространении волны движение передается от одного участка тела к другому. С передачей движения связана передача энергии. Передача энергии без передачи вещества — основное свойство всех волн.
Любые волны характеризуются длиной и скоростью их распространения.
Длина волны — это расстояние между ближайшими друг к другу точками волны, колеблющимися в одинаковых фазах (рис. 208). 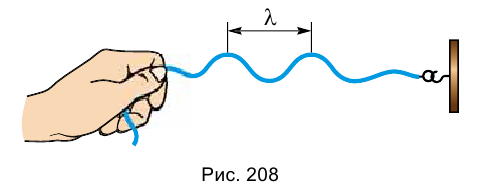
Длину волны обозначают греческой буквой А. (лямбда). Ее единицей является один метр (1 м).
Волны любого происхождения распространяются в пространстве не мгновенно, а с определенной скоростью. Например, можно увидеть, как чайка летит над морем будто все время над одним гребнем волны. В этом случае скорость полета чайки равна скорости распространения волны.
А как можно определить скорость распространения волны?
Вы уже знаете, что любое колебание характеризуется периодом колебаний, то есть временем, после которого колебания повторяются. Тогда можно сказать, что за один период волна распространяется на расстояние 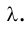
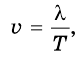
где v — скорость распространения волны (м/с); 
Так как период и частота связаны соотношением 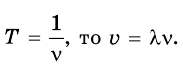
Пример №1
Определите скорость распространения волны на воде, если ее длина равна 180 м, а период колебаний — 15 с.
Решение
По формуле 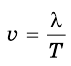
v = 180 м : 15 с = 12 м/с.
Ответ: 12 м/с.
Пример №2
Каково основное свойство механической волны?
Ответ: переносить энергию.
Интерференция волн
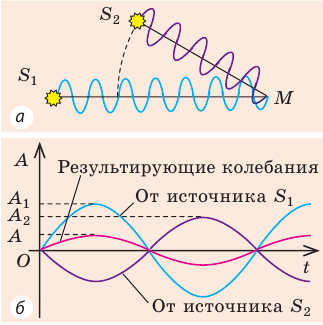
Для волн не очень больших амплитуд справедлив принцип суперпозиции: если в точку пространства приходят волны от нескольких источников, то эти волны накладываются друг на друга. В результате такого наложения в некоторых точках пространства может наблюдаться постоянное усиление колебаний, а в некоторых — ослабление. Выясним, почему и когда это происходит. Пусть в некоторую точку M поступают две когерентные волны — волны от двух источников 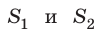
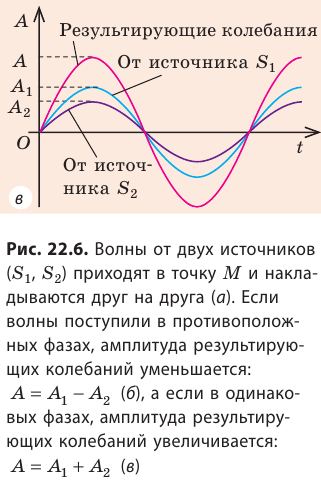
Если волны приходят в точку М в противоположных фазах (в один и тот же момент времени одна волна «толкает» точку М вверх, а вторая «толкает» ее вниз), то волны будут постоянно гасить друг друга (рис. 22.6, б). Если же волны приходят в точку М в одинаковых фазах, то в точке M будут все время наблюдаться колебания с увеличенной амплитудой (рис. 22.6, в). явление наложения волн, вследствие которого в некоторых точках пространства наблюдается устойчивое во времени усиление или ослабление результирующих колебаний, называют интерференцией.
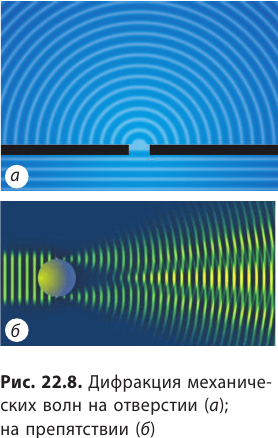
Дифракция волн
Судно, плывущее по морю, образует на поверхности воды волну. Если на своем пути волна встретит скалу или торчащую из воды ветку, то за скалой образуется тень (то есть непосредственно за скалу волна не проникает), а за веткой тень не образуется (волна ветку огибает).
Явление огибания волнами препятствий называют дифракцией (от лат. difractus — разломанный) (рис. 22.8).
В приведенном примере дифракция волны происходит на ветке, но не происходит на скале. Но это не всегда так. Если скала достаточно удалена от берега, то на некотором расстоянии от скалы тень исчезнет — волна обогнет и скалу. Дело в том, что дифракция наблюдается в двух случаях: 1) когда линейные размеры препятствий, на которые находит волна (или размеры отверстий, сквозь которые проходит волна), сопоставимы с длиной волны; 2) когда расстояние от препятствия до места наблюдения намного больше размера препятствия.
- Распространение в пространстве колебаний вещества или поля называют волной. Механической волной называют распространение колебаний в упругой среде.
- Волна распространяется в пространстве не мгновенно, а с конечной скоростью. При распространении волны происходит перенос энергии без переноса вещества. В некоторых точках пространства вследствие наложения волн друг на друга может наблюдаться устойчивое во времени усиление или ослабление результирующих колебаний — это явление называют интерференцией. Волны могут огибать препятствия — это явление называют дифракцией.
- Волну, в которой частицы среды колеблются перпендикулярно направлению распространения волны, называют поперечной. Волну, в которой частицы среды колеблются вдоль направления распространения волны, называют продольной.
- Волна периодична во времени и пространстве. Периодичность волны во времени характеризуется периодом колебаний каждой отдельной точки волны. Периодичность волны в пространстве характеризуется длиной волны. Длина волны — это расстояние, на которое распространяется волна за время, равное периоду колебаний. Длина λ, частота ν и скорость v распространения волны связаны формулой волны: v = λν .
Звуковые волны
Звучание флейты, шум мегаполиса, шорох травы, грохот водопада, человеческая речь, музыкальный звук, шум, акустический резонанс. Все это связано с распространением в пространстве определенных механических волн, которые называют звуковыми волнами. Их изучает акустика — наука о звуке. С элементами акустики вы начали знакомиться в курсе физики 9 класса. Итак, вспоминаем и узнаем новое.
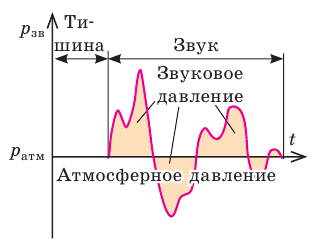
Звуковые (акустические) волны — это механические волны с частотами от 20 Гц до 20 кГц. Звуковые волны обычно доходят до уха через воздух — в виде последовательных сгущений и разрежений (то есть в воздухе звуковые волны являются продольными). В зонах сгущений (разрежений) давление воздуха незначительно больше (меньше) атмосферного (рис. 23.1).
Рис. 23.1. Человеческое ухо воспринимает звуковые волны с избыточным (звуковым) давлением примерно от 20 мкПа (0 децибелов — порог слышимости) до 20 Па (120 децибелов — болевой порог). Для сравнения 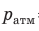
Звук — механическая волна, потому все свойства волнового движения касаются и звука.
- Звук распространяется в среде с конечной скоростью, зависящей от температуры, плотности, состава и других характеристик среды. Так, в жидкостях звук распространяется быстрее, чем в газах, и медленнее, чем в твердых телах. Скорость распространения звука обычно увеличивается с увеличением температуры среды (в воздухе при температуре 0 °С скорость распространения звука составляет около 330 м/с, а при 20 °С — 340 м/с). Кроме того, чем меньше масса молекул среды, тем быстрее распространяется звук.
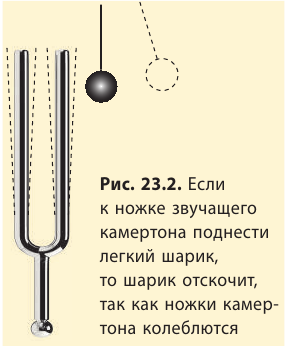
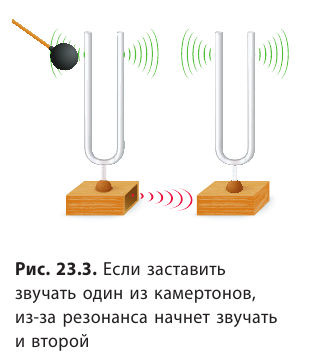
- Источником звука является колеблющееся тело (рис. 23.2). Такие колебания могут быть вынужденными (диффузор громкоговорителя), свободными (струна гитары), автоколебаниями (струны смычковых инструментов).
- Звук не распространяется в вакууме.
- При распространении звука не происходит переноса вещества, но происходит перенос энергии.
- Звуковые волны могут накладываться друг на друга (явление интерференции); могут огибать препятствия (явление дифракции).
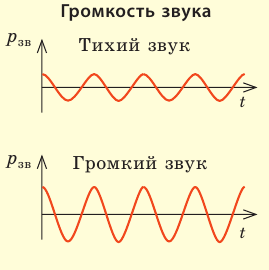
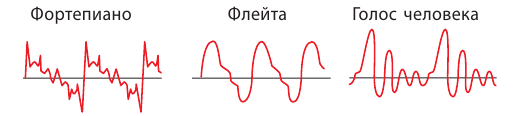
Как связаны субъективные и объективные характеристики звука
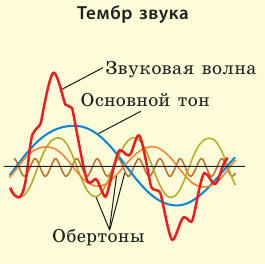
Все физические величины, характеризующие механические волны (амплитуда, частота, длина, энергия), являются и характеристиками звука. Эти величины не зависят от особенностей восприятия звука человеком, поэтому их называют объективными, или физическими, характеристиками звука. Субъективные характеристики звука (громкость, высота, тембр) обусловлены особенностями слуха человека, поэтому их называют физиологическими. Понятно, что физические и физиологические характеристики звука связаны (см. таблицу).
- Заказать решение задач по физике
| Субъективные (физиологические) характеристики звука | |||||
|---|---|---|---|---|---|
 | |||||
| Обратите внимание! Громкий звук может привести к ухудшению слуха и даже к глухоте, особенно это касается прослушивания громкой музыки в наушниках. Слушать музыку в наушниках следует при минимальной громкости! | |||||
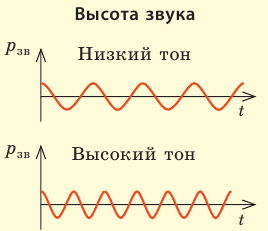 | Высота звука определяется в основном частотой звуковой волны: чем больше ее частота, тем выше тон звука. Например, ноте «ля» первой октавы соответствует частота 440 Гц; ноте «ля» второй октавы — частота 880 Гц. Свойство человеческого уха различать звуки по их частоте также зависит от интенсивности звуков. При увеличении интенсивности звука его высота кажется более низкой. | ||||
 | |||||
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Волновое движение в физике
- Продольные и поперечные волны в физике
- Звуковые волны в физике
- Электрическое поле в физике
- Электромагнитные явления в физике
- Электромагнитные волны и их свойства
- Магнитные явления в физике
- Магнитный поток
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Механические волны
Когда в каком-нибудь месте твердой, жидкой или газообразной среды происходит возбуждение колебаний частиц, результатом взаимодействия атомов и молекул среды становится передача колебаний от одной точки к другой с конечной скоростью.
Волна – это процесс распространения колебаний в среде.
Виды механических волн
Различают следующие виды механических волн:
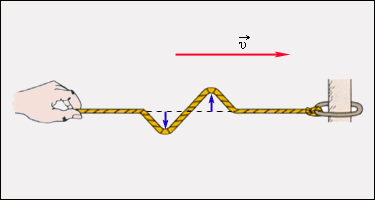
Поперечная волна: частицы среды смещаются в направлении, перпендикулярном направлению распространения механической волны.
Пример: волны, распространяющиеся по струне или резиновому жгуту в натяжении (рисунок 2 . 6 . 1 );
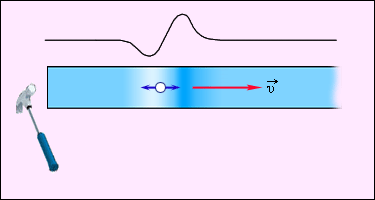
Продольная волна: частицы среды смещаются в направлении распространения механической волны.
Пример: волны, распространяющиеся в газе или упругом стержне (рисунок 2 . 6 . 2 ).
Интересно, что волны на поверхности жидкости включают в себя и поперечную, и продольную компоненты.
Укажем важное уточнение: когда механические волны распространяются, они переносят энергию, форму, но не переносят массу, т.е. в обоих видах волн переноса вещества в направлении распространения волны не происходит. Распространяясь, частицы среды совершают колебания около положений равновесия. При этом, как мы уже сказали, волны переносят энергию, а именно энергию колебаний от одной точки среды к другой.
Рисунок 2 . 6 . 1 . Распространение поперечной волны по резиновому жгуту в натяжении.
Рисунок 2 . 6 . 2 . Распространение продольной волны по упругому стержню.
Модель твердого тела
Характерная черта механических волн – их распространение в материальных средах в отличие, например, от световых волн, способных распространяться и в пустоте. Для возникновения механического волнового импульса необходима среда, имеющая возможность запасать кинетическую и потенциальную энергии: т.е. среда должна иметь инертные и упругие свойства. В реальных средах эти свойства получают распределение по всему объему. К примеру, каждому небольшому элементу твердого тела присуща масса и упругость. Самая простая одномерная модель такого тела представляет из себя совокупность шариков и пружинок (рисунок 2 . 6 . 3 ).
Рисунок 2 . 6 . 3 . Простейшая одномерная модель твердого тела.
В этой модели инертные и упругие свойства разделены. Шарики имеют массу m , а пружинки – жесткость k . Такая простая модель дает возможность описать распространение продольных и поперечных механических волн в твердом теле. При распространении продольной волны шарики смещаются вдоль цепочки, а пружинки растягиваются или сжимаются, что есть деформация растяжения или сжатия. Если подобная деформация происходит в жидкой или газообразной среде, ее сопровождает уплотнение или разрежение.
Отличительная особенность продольных волн заключается в том, что они способны распространяться в любых средах: твердых, жидких и газообразных.
Если в указанной модели твердого тела один или несколько шариков получают смещение перпендикулярно всей цепочке, можно говорить о возникновении деформации сдвига. Пружины, получившие деформацию в результате смещения, будут стремиться вернуть смещенные частицы в положение равновесия, а на ближайшие несмещенные частицы начнет оказываться влияние упругих сил, стремящихся отклонить эти частицы от положения равновесия. Итогом станет возникновение поперечной волны в направлении вдоль цепочки.
В жидкой или газообразной среде упругая деформация сдвига не возникает. Смещение одного слоя жидкости или газа на некоторое расстояние относительно соседнего слоя не приведет к появлению касательных сил на границе между слоями. Силы, которые оказывают воздействие на границе жидкости и твердого тела, а также силы между соседними слоями жидкости всегда направлены по нормали к границе – это силы давления. Аналогично можно сказать и о газообразной среде.
Таким образом, появление поперечных волн невозможно в жидкой или газообразной средах.
В плане практического применения особый интерес представляют простые гармонические или синусоидальные волны. Они характеризуются амплитудой A колебания частиц, частотой f и длиной волны λ . Синусоидальные волны получают распространение в однородных средах с некоторой постоянной скоростью υ .
Запишем выражение, показывающее зависимость смещения y ( x , t ) частиц среды из положения равновесия в синусоидальной волне от координаты x на оси O X , вдоль которой распространяется волна, и от времени t :
y ( x , t ) = A cos ω t — x υ = A cos ω t — k x .
В приведенном выражении k = ω υ – так называемое волновое число, а ω = 2 π f является круговой частотой.
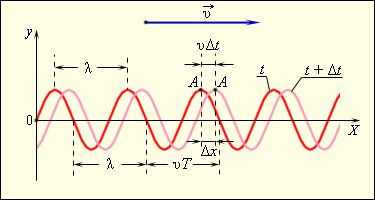
Бегущая волна
Рисунок 2 . 6 . 4 демонстрирует «моментальные фотографии» поперечной волны в момент времени t и t + Δ t . За промежуток времени Δ t волна перемещается вдоль оси O X на расстояние υ Δ t . Подобные волны носят название бегущих волн.
Рисунок 2 . 6 . 4 . «Моментальные фотографии» бегущей синусоидальной волны в момент времени t и t + Δ t .
Длина волны λ – это расстояние между двумя соседними точками на оси O X , испытывающими колебание в одинаковых фазах.
Расстояние, величина которого есть длина волны λ , волна проходит за период Т . Таким образом, формула длины волны имеет вид: λ = υ T , где υ является скоростью распространения волны.
С течением времени t происходит изменение координаты x любой точки на графике, отображающем волновой процесс (к примеру, точка А на рисунке 2 . 6 . 4 ), при этом значение выражения ω t – k x остается неизменным. Спустя время Δ t точка А переместится по оси O X на некоторое расстояние Δ x = υ Δ t . Таким образом:
ω t — k x = ω ( t + ∆ t ) — k ( x + ∆ x ) = c o n s t или ω ∆ t = k ∆ x .
Из указанного выражения следует:
υ = ∆ x ∆ t = ω k или k = 2 π λ = ω υ .
Становится очевидно, что бегущая синусоидальная волна имеет двойную периодичность – во времени и пространстве. Временной период является равным периоду колебаний T частиц среды, а пространственный период равен длине волны λ .
Волновое число k = 2 π λ – это пространственный аналог круговой частоты ω = — 2 π T .
Сделаем акцент на том, что уравнение y ( x , t ) = A cos ω t + k x является описанием синусоидальной волны, получающей распространение в направлении, противоположном направлению оси O X , со скоростью υ = — ω k .
Когда бегущая волна получает распространение, все частицы среды гармонически колеблются с некоторой частотой ω . Это означает, что как и при простом колебательном процессе, средняя потенциальная энергия, являющаяся запасом некоторого объема среды, есть средняя кинетическая энергия в том же объеме, пропорциональная квадрату амплитуды колебаний.
Из вышесказанного можно сделать вывод, что, когда бегущая волна получает распространение, появляется поток энергии, пропорциональный скорости волны и квадрату ее амплитуды.
Скорость распространения волны
Бегущие волны движутся в среде с определенными скоростями, находящимися в зависимости от типа волны, инертных и упругих свойств среды.
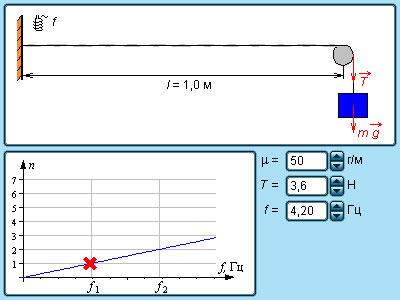
Скорость, с которой поперечные волны распространяются в натянутой струне или резиновом жгуте, имеет зависимость от погонной массы μ (или массы единицы длины) и силы натяжения T :
Скорость, с которой продольные волны распространяются в безграничной среде, рассчитывается при участии таких величин как плотность среды ρ (или масса единицы объема) и модуль всестороннего сжатия B (равен коэффициенту пропорциональности между изменением давления Δ p и относительным изменением объема Δ V V , взятому с обратным знаком):
Таким образом, скорость распространения продольных волн в безграничной среде, определяется по формуле:
При температуре 20 ° С скорость распространения продольных волн в воде υ ≈ 1480 м / с , в различных сортах стали υ ≈ 5 – 6 к м / с .
Если речь идет о продольных волнах, получающих распространение в упругих стержнях, запись формулы для скорости волны содержит не модуль всестороннего сжатия, а модуль Юнга:
Для стали отличие E от B незначительно, а вот для прочих материалов оно может составлять 20 – 30 % и больше.
Рисунок 2 . 6 . 5 . Модель продольных и поперечных волн.
Стоячая волна
Предположим, что механическая волна, получившая распространение в некоторой среде, встретила на пути некое препятствие: в этом случае характер ее поведения резко изменится. К примеру, на границе раздела двух сред с различающимися механическими свойствами волна частично отразится, а частично проникнет во вторую среду. Волна, пробегающая по резиновому жгуту или струне, отразится от зафиксированного конца, и возникнет встречная волна. Если у струны зафиксированы оба конца, появятся сложные колебания, являющиеся итогом наложения (суперпозиции) двух волн, получающих распространение в противоположных направлениях и испытывающих отражения и переотражения на концах. Так «работают» струны всех струнных музыкальных инструментов, зафиксированные с обоих концов. Схожий процесс возникает при звучании духовых инструментов, в частности, органных труб.
Если волны, распространяющиеся по струне во встречных направлениях, обладают синусоидальной формой, то при определенных условиях они образуют стоячую волну.
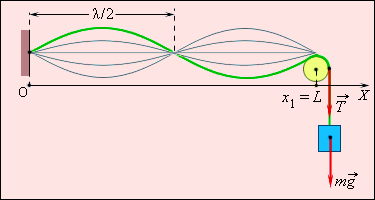
Допустим, струна длины l зафиксирована таким образом, что один из ее концов расположен в точке x = 0 , а другой – в точке x 1 = L (рисунок 2 . 6 . 6 ). В струне имеется натяжение T .
Рисунок 2 . 6 . 6 . Возникновение стоячей волны в струне, зафиксированной на обоих концах.
По струне одновременно пробегают в противоположных направлениях две волны с одинаковой частотой:
- y 1 ( x , t ) = A cos ( ω t + k x ) – волна, распространяющаяся справа налево;
- y 2 ( x , t ) = A cos ( ω t — k x ) – волна, распространяющаяся слева направо.
Точка x = 0 — один из зафиксированных концов струны: в этой точке падающая волна y 1 в результате отражения создает волну y 2 . Отражаясь от зафиксированного конца, отраженная волна входит в противофазу с падающей. В соответствии с принципом суперпозиции (что есть экспериментальный факт) колебания, созданные встречными волнами во всех точках струны, суммируются. Из сказанного следует, что итоговое колебание в каждой точке определяется как сумма колебаний, вызванных волнами y 1 и y 2 в отдельности. Таким образом:
y = y 1 ( x , t ) + y 2 ( x , t ) = ( — 2 A sin ω t ) sin k x .
Приведенное выражение является описанием стоячей волны. Введем некоторые понятия, применимые к такому явлению как стоячая волна.
Узлы – точки неподвижности в стоячей волне.
Пучности – точки, расположенные между узлами и колеблющиеся с максимальной амплитудой.
Если следовать данным определениям, для возникновения стоячей волны оба зафиксированных конца струны должны являться узлами. Указанная ранее формула отвечает этому условию на левом конце ( x = 0 ) . Чтобы условие было выполнено и на правом конце ( x = L ) , необходимо чтобы k L = n π , где n является любым целым числом. Из сказанного можно сделать вывод, что стоячая волна в струне появляется не всегда, а только тогда, когда длина L струны равна целому числу длин полуволн:
l = n λ n 2 или λ n = 2 l n ( n = 1 , 2 , 3 , . . . ) .
Набору значений λ n длин волн соответствует набор возможных частот f
f n = υ λ n = n υ 2 l = n f 1 .
В этой записи υ = T μ есть скорость, с которой распространяются поперечные волны по струне.
Каждая из частот f n и связанный с ней тип колебания струны называется нормальной модой. Наименьшая частота f 1 носит название основной частоты, все прочие ( f 2 , f 3 , … ) называются гармониками.
Рисунок 2 . 6 . 6 иллюстрирует нормальную моду для n = 2 .
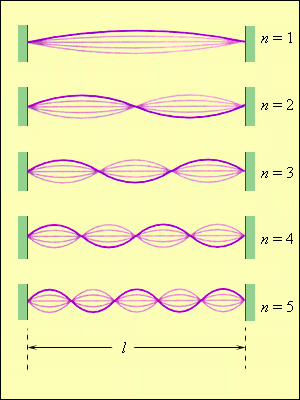
Стоячая волна не обладает потоком энергии. Энергия колебаний, «запертая» в отрезке струны между двумя соседними узлами, не переносится в остальные части струны. В каждом таком отрезке происходит периодическое (дважды за период T ) преобразование кинетической энергии в потенциальную и обратно, подобно обычной колебательной системе. Однако, здесь имеется различие: если груз на пружине или маятник имеют единственную собственную частоту f 0 = ω 0 2 π , то струна характеризуется наличием бесконечного числа собственных (резонансных) частот f n . На рисунке 2 . 6 . 7 показано несколько вариантов стоячих волн в струне, зафиксированной на обоих концах.
Рисунок 2 . 6 . 7 . Первые пять нормальных мод колебаний струны, зафиксированной на обоих концах.
Согласно принципу суперпозиции стоячие волны различных видов (с разными значениями n ) способны одновременно присутствовать в колебаниях струны.
Рисунок 2 . 6 . 8 . Модель нормальных мод струны.
Физика волновых процессов
ФИЗИКА ВОЛНОВЫХ ПРОЦЕССОВ
1. Волновое уравнение. Гармонические волны. Уравнение Гельмгольца. Фазовый фронт, фазовая скорость, длина волны. Стоячие волны. Неоднородные плоские волны. Цилиндрические и сферические волны.
2. Плоские электромагнитные волны в поглощающей среде. Глубина проникновения. Поток мощности. Скорость волны. Поверхностный импеданс металлов. Скин-слой.
3. Дисперсия волн. Волновой пакет. Фазовая и групповая скорости. Нормальная и аномальная дисперсии. Дисперсионное уравнение.
4. Прохождение плоской волны через границу раздела двух сред. Коэффициенты Френеля. Явление полного внутреннего отражения. Угол Брюстера. Приближенные граничные условия Леонтовича.
5. Плоские электромагнитные волны в анизотропных средах. Продольное и поперечное распространение в намагниченной плазме. Обыкновенная и необыкновенная волны. Эффекты Фарадея и Коттона-Мутона.
6. Излучение волн. Ближняя и дальняя зоны. Диаграмма направленности линейного излучателя. Понятие области мнимых углов. Излучение волн плоским раскрывом.
7. Электромагнитные волны в направляющих системах. ТЕ, ТМ и ТЕМ волны. Критическая частота. Длина волны в направляющей системе. Волновое сопротивление линии передачи.
8. Приближение геометрической оптики. Уравнение эйконала. Световые лучи. Область применимости лучевого приближения. Принцип Ферма. Рефракция.
Волновое уравнение. Гармонические волны. Уравнение Гельмгольца. Фазовый фронт, фазовая скорость, длина волны. Стоячие волны. Неоднородные плоские волны. Цилиндрические и сферические волны.
Зададим некоторое возмущение, распространяющееся в пространстве, в виде U=U(at–bs), где t – текущее время; s – пространственная координата, вдоль которой распространяется возмущение, и продифференцируем 2 раза по t и 2 раза по s:


сравнивая (1) и (2) и учитывая, что 

Перейдя к характеристическим переменным 


Здесь предполагается, что U изменяется только в одном направлении s, задаваемом единичным вектором m, тогда s = (mr) (r – радиус-вектор точки наблюдения). В некоторый момент времени t=to U() = const, если s = const. Т. к. (mr) = const – уравнение плоскости, то 
Если 

(приведенное волновое уравнение или уравнение Гельмгольца). Это уравнение описывает распространение гармонических свободных волн. Величина 





Если волна распространяется в направлении единичного вектора m, можем ввести вектор k = km (волновой вектор), тогда ks = (kr), и поверхность равных фаз ks = const определяется уравнением плоскости (kr) = const, нормальной к направлению распространения волны. Если k – вещественный вектор, то А=const всюду. Такая волна называется однородной плоской волной.
Функция F удовлетворяет однородному уравнению Гельмгольца и в том случае, если
k=k+ik но при условии, что |k|2 = k2 – вещественно, т. е. (kk) = 0, а |k|2–|k|2 = k2. В этом случае решение 
Для произвольной зависимости от координат однородное волновое уравнение имеет следующий вид 

В цилиндрических координатах 






В сферических координатах 




1. , , Сухоруков волн. — М.: Наука, 1979.
2. Вайнштейн волны. — М.: Радио и связь, 1988.
Плоские электромагнитные волны в поглощающей среде. Скорость волны. Глубина проникновения. Поверхностный импеданс металлов. Скин-слой. Поток мощности.
В средах с потерями (s ¹ 0) имеем: [ÑH] = iweE+sE = iw (e — is /w)E = iw




mотн= 4p10-7[Гн/м] ). Пусть в такой среде вдоль оси z распространяется плоская гармоническая волна, удовлетворяющая уравнениям: 







Здесь: a – коэффициент затухания, b – коэффициент фазы, Zo – волновое сопротивление среды

Таким образом, в поглощающей среде амплитуда уходящей волны убывает по экспоненциальному закону,
уменьшаясь в e раз на расстоянии d=1/a, которое называется глубина проникновения (скин-слой), длина волны l=2p/b и фазовая скорость vф=w /b уменьшаются по сравнению с непоглощающей средой, в среде с электрическими потерями Ну отстает по фазе от Еx на величину d /2 (в среде с магнитными потерями, когда комплексной величиной является m , Ну опережает Еx), поверхность равных фаз совпадает с поверхностью равных амплитуд. Для сред с tg d >>1 (металлы) 



В среде с потерями поток мощности через единицу поверхности П=[EH*] становится комплексным.
Мгновенное значение Пz равно
Пz=











 |
Компоненты поля в первой и во второй средах имеют вид:
2. Параллельно поляризованная волна
Поле падающей волны:
компоненты поля отраженной волны:
компоненты поля преломленной волны:

На границе раздела (у=0) для любых z должно выполняться
Нпадexp(-ik1zsinq) + Нотрexp(-ik1zsinq¢) = Нпрexp(-ik2zsiny),
Откуда следуют законы Снелиуса: sinq = sinq¢ и k1sinq = k2siny.
Учитывая Еt1= (НпадZ01+ НотрZ01)cosq и Еt2= НпрZ02cosy, запишем граничные условия для параллельно поляризованной волны в виде:



где Rêê и Têê – коэффициенты Френеля для параллельно поляризованной волны. (Rêê – коэффициент отражения, Têê – коэффициент прохождения). R2êê + T2êê= 1.


Компоненты поля в первой и во второй средах имеют вид:
Для диэлектриков m1= m2= m0, и коэффициенты Френеля можно записать в виде:

где 
Анализ этих выражений показывает, что для параллельно поляризованной волны существует угол падения qБ = p/2 – y, при котором R||=0. Этот угол, определяемый из соотношения tgqБ=
Из закона Снелиуса sin y = 


При падении волны из свободного пространства на границу раздела с хорошо проводящей средой, у которой tgd>>1, siny Þ 1, т. е. тангенциальные компоненты поля на поверхности проводника непрерывно переходят в поперечные компоненты поля уходящей вглубь проводника волны. Соотношение между ними можно записать в виде Еt=Zos[Htyo], где Zos – поверхностный импеданс проводящей среды, yo – орт нормали к границе раздела. Это импедансное граничное условие называют приближенным граничным условием Леонтовича.
1. , Зернов поля и волны. — М.: Сов. радио, 1971.
2. , Никольская и распространение радиоволн. М. Наука, 1989
Волны в анизотропных средах
Для изотропных сред, свойства которых не зависят от направления, B = mH и D = eE, где e и m — скалярные величины, следовательно: Bx= mHx, By=mHy, Bz=mHz, Dx= eEx, Dy=eEy, Dy=eEy. Существуют анизотропные среды, которые в разных направлениях имеют различные свойства, т. е. связь между проекциями векторов B и H или D и E описывается соотношениями
Bx= mxxHx+ mxyHy + mxzHz, By= myxHx+ myyHy + myzHz, Bz= mzxHx+ mzyHy + mzzHz, .
Dx= exxEx+ exyEy + exzEz, Dy= eyxEx+ eyyEy + eyzEz, Dz= ezxEx+ ezyEy + ezzEz, .
Формально эту связь принято представлять в виде 



В природе неизвестны вещества, у которых одновременно e и m имеют тензорный характер, поэтому в дальнейшем будем рассматривать вещества, обладающие или диэлектрической или магнитной анизотропией.
Типичными представителями анизотропных сред являются намагниченные плазма и феррит.
Плазма — электрически нейтральный газ, в котором значительная часть атомов или молекул ионизирована
Под действием электрического поля на каждый электрон действует сила Fk= –Eeo (кулоновское взаимодействие). Если движущийся со скоростью v электрон находится в постоянном магнитном поле Н=, на него действует сила Лоренца Fл = –eomo[vH=], вследствие чего электрон получает также вращательное движение. В этом случае уравнение движения электрона имеет вид: 





Продольное распространение плоской волны в намагниченной плазме
При продольном распространении (вдоль H=) 






ik


(k2–w2exmo)E0y= iw2bmoE0x, (k2–w2exmo) = ±w2bmo или k1,2 = w

Таким образом, получили два решения, следовательно в намагниченной плазме одновременно распространяются две волны с волновыми числами k1=w 




Ey1=E01sin(wt–k1z) поляризации левого Ex2=E02sin(wt–k2z) при ex=b, k2 Þ 0, поэтому ее



Hy1= –


Необыкновенная волна при w Þ wm исчезает вследствие резонансного поглощения (явление гиромагнитного резонанса). Полное поле можно представить в виде: Еx=Ex1+Ex2=2Eocos[0.5(k1–k2)z]cos[wt–0.5(k1–k2)z], Еy=Ey1+Ey2=2Eosin[0.5(k1–k2)z]cos[wt–0.5(k1–k2)z], в каждый момент времени Еx и Еy синфазны, угол наклона вектора Е относительно оси x: q = arctg(Ex/Ey) = 0.5(k1–k2)z, т. е. поле имеет линейную поляризацию, но плоскость поляризации медленно вращается при распространении волны. Это явление называется эффект Фарадея. Угол, на который поворачивается плоскость поляризации при прохождении волной единицы длины q! = 0.5(k1–k2), называется постоянная Фарадея. Среды, в которых наблюдается эффект Фарадея, называются гиротропными (вращающими). Этот эффект невзаимный, т. к. при изменении направления Н= меняет знак b. Поскольку Z01 ¹Z02, поле Н имеет эллиптическую поляризацию.
Поперечное распространение в намагниченной плазме
При поперечном распространении (вдоль оси х) 








kE0z = wmoH0y волна «не чувствует» постоянного магнитного поля и называется обыкновенной. Волновое сопротивление обыкновенной волны Zоб=


kH0z = w(ibE0x+ exE0y) E0x находится в квадратуре с E0y, т. е. вектор Ен вращается в плоскости x0y.







Аналогичные явления имеют место и при распространении волн в намагниченном феррите – веществе, обладающем магнитными свойствами ферромагнетиков (mотн=5¸10000) и электрическими свойствами диэлектриков (eотн=5¸20). В магнитном поле магнитная ось атома прецессирует вокруг направления поля Н=, вследствие чего магнитная проницаемость феррита становится тензором



Литература. , Зернов поля и волны. — М.: Сов. радио, 1971.
Излучение волн. Ближняя и дальняя зоны. Диаграмма направленности линейного излучателя. Понятие области мнимых углов. Излучение волн плоским раскрывом.
Излучение – процесс преобразования энергии источника в энергию свободных волн. Математически задача сводится к решению неоднородного волнового уравнения. В случае электромагнитных волн удобнее использовать векторные потенциалы: Ñ2Ae+ k2Ae = –j ст e, Ñ2Am+ k2Am = –j ст m, где Ae и Am– электрический и магнитный векторные потенциалы, j ст e и j ст m– объемные плотности электрических и магнитных сторонних токов, заданных в объеме Va. Используя метод функции Грина, запишем решение в виде:

где 



В зависимости от расстояния до точки наблюдения используются разные приближения:
а) при r >> r¢, дальняя зона (зона Фраунгофера) в показателе экспоненты используется первое приближение: r @ rо– r¢cosa. Минимальное значение rмин, (граница дальней зоны) начиная с которого можно пользоваться этим приближением, определяется из условия (r¢2sin2a)/2ro
выражение (1) имеет вид

При вычислении Е и Н по формулам (2) отбрасываются слагаемые, пропорциональные r–2 и r–3. Тогда Еq= – ik(ZоАqе+Аjм), Еj=–ik(ZоАjе+Аqм), Еr=0; Нj= Еq ¤ Zо, Нq= –Еj ¤ Zо, Нr=0; где Zо– волновое сопротивление среды;
Аq=Аxcosq cosj+Аycosq sinj +Аzsinq , Аj= –Аxsinj +Аycosj, Аr=Аxsinq cosj+Аysinq sinj + Аzcosq.
В общем случае поле в дальней зоне можно представить в виде: Е= Ео

При r l быстрее изменяется fc(q), поэтому рассмотрим зависимость множителя системы от скорости волны тока, определяемой значением b. Введем величину y=kcosq, имеющую смысл пространственной частоты (–¥ k, называется областью мнимых углов, т. к. при этом cosq>1. Видно, что уменьшение скорости волны тока приводит к смещению максимума ДН от нормали к оси излучателя. Если скорость волны тока меньше скорости света (b>k), большая часть энергии “излучается” в область мнимых углов, т. е. отсутствует в дальней зоне и находится вблизи излучателя.
Для синфазного излучателя Dq0,5=51оl / L, УБЛ=0.21.
Излучение волн плоским раскрывом (апертурой)
Пусть на прямоугольной площадке, расположенной в плоскости x,y задано распределение поверхностных токов Je, m(x¢, y¢). В дальней зоне 

Ej= –ik(ZoAeycosj– Amx cosqcosj)= 
является поверхность с заданным на ней распределением электромагнитного поля, например раскрыв рупорной антенны, то согласно принципу эквивалентных токов Je=[Hn], Jm= – [En]. В этом случае Jmx= Eаy, Jey= – Hаx= – Eаy/Zф (здесь Zф= Eаy/Hаx – сопротивление фронта волны, возбуждающей раскрыв) и выражения для полей имеют вид:
Таким образом, излученное поле является суперпозицией сферических волн, имеет в общем случае эллиптическую поляризацию и диаграмма направленности излучателя может быть представлена в виде произведения множителя элемента на множитель системы: f(q, j) = fэ (q, j)fc(q, j), где fэ (q) = 





1. , , Грудинская и распространение радиоволн. — М.:Сов. радио,1979.
Электромагнитные волны в направляющих системах. ТЕ, ТМ и ТЕМ волны. Критическая частота. Длина волны в направляющей системе. Волновое сопротивление линии передачи.
Плоские однородные волны – простейший тип волнового процесса. При наличии границ возникают неоднородные плоские волны, распространяющиеся вдоль этих границ, т. е. возникают плоские направляемые волны. Это делает возможным передачу энергии на большие расстояния с минимальными потерями. Варианты конструктивного исполнения направляющих систем (линий передачи) приведены на рисунке.
Будем считать эти системы продольно однородными (их свойства сохраняются в одном прямолинейном направлении, например, вдоль оси z). Свободные плоские гармонические волны, способные распространяться в направляющей системе, определяются из однородных уравнений Гельмгольца: Ñ2Е + k2E = 0, Ñ2H + k2H = 0. В отличие от плоской волны в неограниченном пространстве, в направляющих системах могут существовать неоднородные плоские волны, имеющие продольную составляющую поля Еz или Нz. Связь между продольными и поперечными составляющими поля определим, используя метод разделения переменных, т. е. полагая Е = Е^(x,y)×exp(±igz), H = H^(x,y)×exp(±igz). Здесь g – продольное волновое число, определяющее скорость распространения волны вдоль z. Для поперечных компонент поля имеем Ñ2Е^+ (k2– g2) E^= 0, Ñ2Н^+ (k2– g2) Н^= 0, где (k2– g2) = c2 – поперечное волновое число, k2 = w2em, e и m – параметры среды, заполняющей линию передачи. Используя координатную запись однородных уравнений Максвелла относительно комплексных амплитуд Е и Н, имеем:



rot E = –iwmH 


в векторной форме имеем:

поперечные – ТЕМ или Т волны (отсутствуют продольные составляющие поля),
электрические – ТМ или Е волны (имеется продольная составляющая электрического поля),
магнитные – ТЕ или Н волны (имеется продольная составляющая магнитного поля),
гибридные – ЕН волны (имеется продольные составляющие электрического и магнитного поля).
Критическая частота: для волн Е и Н типа из c2 = (k2– g2) следует, что 
exp(–igz), т. е. амплитуда волны, распространяющейся вдоль z остается постоянной и меняется только фаза. Если c > k, то g – мнимая величина, следовательно, постоянной остается фаза и по экспоненте убывает амплитуда. При g= 0 имеем: c = k = 2pfкр 



Для ТЕМ волн (Еz =0 и Нz = 0) c2= 0, следовательно, g = k и fкр= 0, т. е. передача энергии возможна на всех частотах, включая нулевую (постоянный ток).
Волновое сопротивление линий передачи определяется исходя из следующих соображений:
используя систему уравнений, связывающих продольные и поперечные составляющие поля, получаем
для Е(ТМ) волн (Нz=0): 




Для Н(ТЕ) волн (Еz=0): 










изменение n на длине волны должно быть > Ñ2A – это условие связано с кривизной поверхности равных амплитуд rА и может быть записано в виде 2pnrA/l >>l/2pnA2, т. е. радиус кривизны ПРА, отнесенный к l, должен быть >> l. Чтобы пренебречь дифракционными явлениями размер фронта волны D должен быть >> l/n. Эти условия не выполняются в точках, где пересекаются лучи (фокус оптических систем); в средах с резкими неоднородностями; в мутных средах; при прохождении поверхностей с поглощающими экранами и т. д.
В неоднородной среде луч, соединяющий две точки р1 и р2, является кривой линией. Для каждой точки луча имеем: dL= (grad L×dr)=| grad L||dr|=k0n(r)dl, где dr направлен по лучу, dl – элемент длины пути. Изменение фазы вдоль луча равно 



В однородной среде луч – прямая линия. При переходе границы раздела между двумя различными средами луч меняет направление. Соединим лучом точку р1(0,у1) в среде с показателем преломления n1 с точкой р2(а,у2) в среде с показателем преломления n2. Луч пересекает границу раздела в точке (х,0). Полное время распространения света от р1 до р2 равно t =  . Используя условие стационарности
. Используя условие стационарности  , получаем:
, получаем:  . Учитывая, что
. Учитывая, что  ,
,  , где q – угол между направлением луча и нормалью к границе раздела, имеем: n1sinq1 = n2sinq2 – закон преломления.
, где q – угол между направлением луча и нормалью к границе раздела, имеем: n1sinq1 = n2sinq2 – закон преломления.



Для нормального состояния атмосферы 


В зависимости от состояния атмосферы различают следующие типы рефракции:
а) 
г) 
д) 
http://zaochnik.com/spravochnik/fizika/volny/mehanicheskie-volny/
http://pandia.ru/text/78/219/11634.php


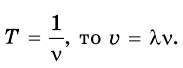

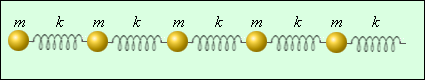




 – фазовая скорость (скорость перемещения фазового фронта). Если b(w), то vф(w), причем может быть vф > c. Означает ли это, что можно передать информацию со скоростью, превышающей скорость света с ?
– фазовая скорость (скорость перемещения фазового фронта). Если b(w), то vф(w), причем может быть vф > c. Означает ли это, что можно передать информацию со скоростью, превышающей скорость света с ? . Каждой составляющей спектра соответствует плоская гармоническая волна, следовательно в точке z > 0 имеем:
. Каждой составляющей спектра соответствует плоская гармоническая волна, следовательно в точке z > 0 имеем:  . Если b=b(w), можем перейти к пространственному спектру, т. е. dw®db, тогда
. Если b=b(w), можем перейти к пространственному спектру, т. е. dw®db, тогда  . Выделим вблизи максимума огибающей спектра с частотой wо участок спектра 2Dw = w1 — w2. Пусть Dw vф (vф
. Выделим вблизи максимума огибающей спектра с частотой wо участок спектра 2Dw = w1 — w2. Пусть Dw vф (vф совпадают по направлению – дисперсия положительная, Если
совпадают по направлению – дисперсия положительная, Если  ). Чтобы гармоническая волна сохраняла форму при любой частоте, необходимо, чтобы в числе решений было решение вида: p = eiw t ± i (kr). Пусть Â переводит р в некоторую функцию q: Â( p) = q. Если qº0, то p – свободная волна в данной среде. Продифференцируем по t, учитывая линейность и однородность Â:
). Чтобы гармоническая волна сохраняла форму при любой частоте, необходимо, чтобы в числе решений было решение вида: p = eiw t ± i (kr). Пусть Â переводит р в некоторую функцию q: Â( p) = q. Если qº0, то p – свободная волна в данной среде. Продифференцируем по t, учитывая линейность и однородность Â:  , т. е.
, т. е.  , где комплексная амплитуда
, где комплексная амплитуда  не зависит от t, но может зависеть от w. Подставив p и q в уравнение Â( p) = q, получим уравнение, не зависящее от t, и содержащее w как параметр. Если продифференцировать по координатам, получим: Ñq=ÑÂ(p)=Â(±ikp)= ±ikÂ(p)= ±ikq, т. е. Ñq=±ikq, следовательно, можно представить q в виде: q=f(w,k)eiw t ± i(kr), где f(w,k) кроме w и k может зависеть только от коэффициентов оператора. При произвольных w и k p = eiw t ± i (kr) не свободная волна, т. к. не является решением уравнения Â( p) = 0. Чтобы определить, какие свободные волны могут распространяться (имеют право на существование) в данной среде, необходимо выбрать такие w и k, чтобы
не зависит от t, но может зависеть от w. Подставив p и q в уравнение Â( p) = q, получим уравнение, не зависящее от t, и содержащее w как параметр. Если продифференцировать по координатам, получим: Ñq=ÑÂ(p)=Â(±ikp)= ±ikÂ(p)= ±ikq, т. е. Ñq=±ikq, следовательно, можно представить q в виде: q=f(w,k)eiw t ± i(kr), где f(w,k) кроме w и k может зависеть только от коэффициентов оператора. При произвольных w и k p = eiw t ± i (kr) не свободная волна, т. к. не является решением уравнения Â( p) = 0. Чтобы определить, какие свободные волны могут распространяться (имеют право на существование) в данной среде, необходимо выбрать такие w и k, чтобы  . Это уравнение называют дисперсионным уравнением. Каждому значению w соответствует решение этого уравнения относительно k, и каждому k – относительно w. Для изотропной среды это уравнение содержит только |k| и его можно привести к виду
. Это уравнение называют дисперсионным уравнением. Каждому значению w соответствует решение этого уравнения относительно k, и каждому k – относительно w. Для изотропной среды это уравнение содержит только |k| и его можно привести к виду  – дисперсионное уравнение для данной среды.
– дисперсионное уравнение для данной среды. . Ищем волну в виде: j = еiw t – i k x – k z. Получаем дисперсионное уравнение:
. Ищем волну в виде: j = еiw t – i k x – k z. Получаем дисперсионное уравнение:  . Отсюда vф= g /w, т. е. vф зависит от w, следовательно, существует нормальная дисперсия (vф
. Отсюда vф= g /w, т. е. vф зависит от w, следовательно, существует нормальная дисперсия (vф , где G – коэффициент изгибной жесткости. Ищем решение в виде: еiw t – i k x, получаем дисперсионное уравнение
, где G – коэффициент изгибной жесткости. Ищем решение в виде: еiw t – i k x, получаем дисперсионное уравнение  , откуда
, откуда  , т. е. имеется аномальная дисперсия (vф
, т. е. имеется аномальная дисперсия (vф q – угол падения, q¢– угол отражения,
q – угол падения, q¢– угол отражения, exp[-ik1(-ycosq+zsinq)],
exp[-ik1(-ycosq+zsinq)], exp[-k1(ycosq¢+zsinq¢)].
exp[-k1(ycosq¢+zsinq¢)]. exp[-ik2(ycosy+zsiny)].
exp[-ik2(ycosy+zsiny)]. откуда
откуда  ,
,  ,
, ,
,  ,
,
















 . Используя условие стационарности
. Используя условие стационарности  , получаем:
, получаем:  . Учитывая, что
. Учитывая, что  ,
,  , где q – угол между направлением луча и нормалью к границе раздела, имеем: n1sinq1 = n2sinq2 – закон преломления.
, где q – угол между направлением луча и нормалью к границе раздела, имеем: n1sinq1 = n2sinq2 – закон преломления.