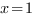Возведем обе части уравнения в третью степень

Возведем обе части уравнения в третью степень

Решите иррациональное уравнение

Попробуем решить иррациональное уравнение методом возведения обеих частей уравнения в одну и ту же степень. Напомним его алгоритм:

• Переходим к более простому уравнению, для чего один или большее число раз выполняем по кругу три следующих действия:
  • Уединяем радикал.
  • Возводим обе части уравнения в одну и ту же степень.
  • Упрощаем вид полученного после возведения в степень уравнения.
• Решаем полученное уравнение.
• Отсеиваем посторонние корни, если раннее мы проводили возведение в четную степень.

Начнем с первого прохода тройки действий – уединим радикал, возведем обе части в степень и упростим полученное уравнение.

Уединение радикала приводит к уравнению .

Теперь возведем обе части уравнения в квадрат, что позволит в дальнейшем избавиться от корня в левой части. Имеем .

Упрощаем вид полученного уравнения при помощи преобразования уравнений. Отталкиваясь от определения корня, заменяем выражение в левой части уравнения тождественно равным ему выражением 2·x+1 , это дает уравнение . Что касается дальнейшего упрощения вида уравнения, то целесообразно по одному из свойств корней вторую степень отправить под кубический корень, то есть, перейти к уравнению .

Как видно, первый проход цикла тройки действий (уединение радикала, возведение обеих частей уравнения в степень и упрощение вида уравнения) позволил избавиться от одного корня, но остался еще один корень. Чтобы избавиться от него, еще раз выполним три уже упомянутых действия.

Радикал у нас уже уединен в правой части. Переходим к возведению в степень.

Степень корня равна трем, поэтому обе части возведем в третью степень: .

Упростим вид полученного уравнения. Для этого заменим выражение в правой части уравнения тождественно равным ему выражением (x+1) 2 , получим (2·x+1) 3 =(x+1) 2 . После этого перенесем это выражение в левую часть: (2·x+1) 3 −(x+1) 2 =0 . Дальше воспользуемся формулами сокращенного умножения квадрат суммы и куб суммы, раскроем скобки, а также сгруппируем и приведем подобные слагаемые:
8·x 3 +12·x 2 +6·x+1−(x 2 +2·x+1)=0 ,
8·x 3 +12·x 2 +6·x+1−x 2 −2·x−1=0 ,
8·x 3 +(12·x 2 −x 2 )+(6·x−2·x)+(1−1)=0 ,
8·x 3 +11·x 2 +4·x=0 .

Так мы получили кубическое уравнение. В еще одном проходе тройки действий нет необходимости, так как полученное уравнение не содержит корней, и мы знаем, как решать кубические уравнения. Поэтому, переходим ко второму этапу алгоритма – решению полученного уравнения.

Для решения полученного кубического уравнения подходит метод разложения на множители. После вынесения за скобки переменной x , уравнение принимает вид x·(8·x 2 +11·x+4)=0 , а оно равносильно совокупности двух уравнений x=0 и 8·x 2 +11·x+4=0 . Отсюда первый корень уравнения очевиден: x₁=0 . Остальные корни найдем, решив квадратное уравнение 8·x 2 +11·x+4=0 . Вычисляем дискриминант D=11 2 −4·8·4=121−128=−7 , он отрицательный, следовательно, квадратное уравнение не имеем действительных корней. Таким образом, кубическое уравнение 8·x 3 +11·x 2 +4·x=0 имеет единственный корень x₁=0 .

Остался последний этап решения – отсеивание посторонних корней. В нашем случае этот этап необходим, так как найденный корень может оказаться посторонним для решаемого иррационального уравнения. Причин для этого две. Первая — выше мы проводили возведение обеих частей уравнения квадрат, а, как известно, это преобразование может привести к появлению посторонних корней. Вторая – мы переходили от уравнения к уравнению , при таком переходе происходит расширение ОДЗ, а это может привести к появлению посторонних корней. Итак, отсеем посторонние корни. Сделаем это через проверку подстановкой. Подставляем x₁=0 в исходное уравнение:

Так как подстановка дала верное числовое равенство, то x₁=0 – корень исходного уравнения. Других корней уравнение не имеет.

На первом этапе мы избавлялись от корней по очереди, в два приема, сначала от квадратного, затем — от кубического. При этом нам пришлось два раза проходить цикл из трех действий – уединение радикала, возведение в степень, упрощение вида. Но можно было избавиться сразу от обоих радикалов, прибегнув к одному возведению в степень. В какую именно степень? Несложно догадаться, что в шестую, или в двенадцатую, или в восемнадцатую, и т.д., то есть, в любую степень, равную кратному показателей корней. Целесообразно брать наименьшее общее кратное (НОК), так как это дает наиболее простое уравнение из возможных. В нашем случае НОК(2, 3)=6 , поэтому, следует выполнять возведение в шестую степень. Покажем, как выглядит решение иррационального уравнения при таком подходе.

Иррациональные уравнения с кубическими радикалами

Разделы: Математика

Тема: «Иррациональные уравнения вида , .»

(Методическая разработка.)

Основные понятия

Иррациональными уравнениями называются уравнения, в которых переменная содержится под знаком корня (радикала) или знаком возведения в дробную степень.

Уравнение вида f(x)=g(x), где хотя бы одно из выражений f(x) или g(x) иррационально является иррациональным уравнением.

Основные свойства радикалов:

• Все радикалы четной степени являются арифметическими, т.е. если подкоренное выражение отрицательно, то радикал не имеет смысла (не существует); если подкоренное выражение равно нулю, то радикал тоже равен нулю; если подкоренное выражение положительно, то значение радикала существует и положительно.
• Все радикалы нечетной степени определены при любом значении подкоренного выражения. При этом радикал отрицателен, если подкоренное выражение отрицательно; равен нулю, если подкоренное выражение равно нулю; положителен, если покоренное выражение положительно.

Методы решения иррациональных уравнений

Решить иррациональное уравнение – значит найти все действительные значения переменной, при подстановке которых в исходное уравнение оно обращается в верное числовое равенство, либо доказать, что таких значений не существует. Иррациональные уравнения решаются на множестве действительных чисел R.

Областью допустимых значений уравнения состоит из тех значений переменной, при которых неотрицательны все выражения, стоящие под знаком радикалов четной степени.

Основными методами решения иррациональных уравнений являются:

а) метод возведения обеих частей уравнения в одну и ту же степень;

б) метод введения новых переменных (метод замен);

в) искусственные приемы решения иррациональных уравнений.

В данной статье остановимся на рассмотрении уравнений определённого выше вида и приведём 6 методов решения таких уравнений.

1 метод. Возведение в куб.

Этот способ требует применения формул сокращённого умножения и не содержит «подводных» камней, т.е. не приводит к появлению посторонних корней.

Пример 1. Решить уравнение

Перепишем уравнение в виде и возведём в куб обе его части. Получим уравнение равносильное данному уравнению ,

,

,

Пример 2. Решить уравнение .

Перепишем уравнение в виде и возведём в куб обе его части. Получим уравнение равносильное данному уравнению

,

,

,

и рассмотрим полученное уравнение как квадратное относительно одного из корней

,

,

следовательно, дискриминант равен 0,а уравнение может иметь решение х=-2.

Проверка:

Замечание: Проверка может быть опущена, в том случае, если дорешивается квадратное уравнение.

2 метод. Возведение в куб по формуле.

По-прежнему будем возводить уравнение в куб, но при этом пользоваться модифицированными формулами сокращенного умножения.

,

(незначительная модификация известной формулы), тогда

Пример3. Решить уравнение .

Возведём уравнение в куб с использованием формул, приведённых выше.

,

Но выражение должно быть равно правой части. Поэтому имеем:

, откуда

.

Теперь при возведении в куб получаем обычное квадратное уравнение:

, и два его корня

,

Оба значения, как показывает проверка, правильные.

Но все ли преобразования здесь равносильны? Прежде чем ответить на этот вопрос, решим ещё одно уравнение.

Пример4. Решить уравнение .

Возводя, как и ранее, обе части в третью степень, имеем:

.

Откуда (учитывая, что выражение в скобках равно ), получаем:

, значит

. Получаем, .Сделаем проверку и убедимся х=0 –посторонний корень.

Ответ: .

Ответим на вопрос: «Почему возникли посторонние корни?»

Равенство влечёт равенство . Заменим с на –с, получим:

и .

Нетрудно проверить тождество

,

Итак, если , то либо , либо . Уравнение можно представить в виде , .

Заменяя с на –с, получаем: если , то либо , либо

Поэтому при использовании этого метода решения обязательно нужно сделать проверку и убедиться что посторонних корней нет.

3 метод. Метод системы.

Пример 5. Решить уравнение .

Введём замену, составим и решим систему уравнений.

Пусть , . Тогда:

откуда очевидно, что

Второе уравнение системы получается таким образом, чтобы линейная комбинация подкоренных выражений не зависела от исходной переменной.

Легко убедиться , что система не имеет решения, следовательно и исходное уравнение не имеет решения.

Ответ: Корней нет.

Пример 6. Решить уравнение .

Введём замену, составим и решим систему уравнений.

Пусть , . Тогда

или

Возвращаясь к исходной переменной имеем:

х=0.

4 метод. Использование монотонности функций.

Прежде чем использовать данный метод обратимся к теории.

Нам понадобятся следующие свойства:

• Если функции y=f(x) и y=g(x) возрастают (убывают) на некотором множестве, то функция y=f(x)+g(x) также возрастает (убывает ) на этом множестве.
• Если функции y=f(x) и y=g(x) возрастают (убывают) на некотором множестве, при чем обе они принимают неотрицательные значения при всех допустимых х, то функция y=f(x)g(x) возрастает (убывает) на данном множестве.
• Если функция y=f(x) монотонная, то уравнение f(x)=a имеет не более одного решения.
• Если функции y=f(x) и y=g(x) имеют разный характер монотонности, то уравнение f(x)=g(x) имеет не более одного решения.
• Функция вида возрастает при к>0 и убывает при к 30.05.2009

Решение иррациональных уравнений

Решение иррациональных уравнений.

В этой статье мы поговорим о способах решения простейших иррациональных уравнений.

Иррациональным уравнением называется уравнение, которое содержит неизвестное под знаком корня.

Давайте рассмотрим два вида иррациональных уравнений, которые очень похожи на первый взгляд, но по сути сильно друг от друга отличаются.

(1)

(2)

В первом уравнении мы видим, что неизвестное стоит под знаком корня третьей степени. Мы можем извлекать корень нечетной степени из отрицательного числа, поэтому в этом уравнении нет никаких ограничений ни на выражение, стоящее под знаком корня, ни на выражение, стоящее в правой части уравнения. Мы можем возвести обе части уравнения в третью степень, чтобы избавиться от корня. Получим равносильное уравнение:

При возведении правой и левой части уравнения в нечетную степень мы можем не опасаться получить посторонние корни.

Пример 1 . Решим уравнение

Возведем обе части уравнения в третью степень. Получим равносильное уравнение:

Перенесем все слагаемые в одну сторону и вынесем за скобки х:

Приравняем каждый множитель к нулю, получим:

, ,

Посмотрим внимательно на второе уравнение: . В левой части уравнения стоит квадратный корень, который принимает только неотрицательные значения. Поэтому, чтобы уравнение имело решения, правая часть тоже должна быть неотрицательной. Поэтому на правую часть уравнения накладывается условие:

=0″ title=»g(x)>=0″/> — это условие существования корней.

Чтобы решить уравнение такого вида, нужно обе части уравнения возвести в квадрат:

(3)

Возведение в квадрат может привести к появлению посторонних корней, поэтому нам надо учесть ОДЗ уравнения:

=0″ title=»f(x)>=0″/> (4)

Однако, неравенство (4) следует из условия (3): если в правой части равенства стоит квадрат какого-то выражения, а квадрат любого выражения может принимать только неотрицательные значения, следовательно левая часть тоже должна быть неотрицательна. Поэтому условие (4) автоматически следует из условия (3) и наше уравнение равносильно системе:

=0> >>< >» title=»delim<1><> =0> >>< >«/>

Пример 2 . Решим уравнение:

.

Перейдем к равносильной системе:

=0> >>< >» title=»delim<1><<2x^2-7x+5=<(1-x)>^2> <1-x>=0> >>< >«/>

Решим первое уравнение системы и проверим, какие корни удовлетворяют неравеству.

,

Неравеству =0″ title=»1-x>=0″/> удовлетворяет только корень

Ответ: x=1

Внимание! Если мы в процессе решения возводим обе части уравнения в квадрат, то нужно помнить, что могут появиться посторонние корни. Поэтому либо нужно переходить к равносильной системе, либо в конце решения СДЕЛАТЬ ПРОВЕРКУ: найти корни и подставить их в исходное уравнение.

Пример 3 . Решим уравнение:

Чтобы решить это уравнение, нам также нужно возвести обе части в квадрат. Давайте в этом уравнении не будем заморачиваться с ОДЗ и условием существования корней, а просто в конце решения сделаем проверку.

Воозведем обе части уравнения в квадрат:

Перенесем слагаемое, содержащее корень влево, а все остальные слагаемые вправо:

Еще раз возведем обе части уравнения в квадрат:

По тереме Виета:

,

Сделаем проверку. Для этого подставим найденные корни в исходное уравнение. Очевидно, что при правая часть исходного уравнения отрицательна, а левая положительна.

При получаем верное равенство.

Ответ: