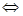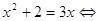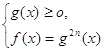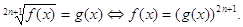Равносильные уравнения. Равносильные преобразования уравнений
Равносильными называют уравнения, имеющие одни и те же корни. Равносильными считаются также уравнения, каждое из которых не имеет корней.
- Уравнения \(x+2=7\) и \(2x+1=11\) равносильны, так как каждое из них имеет единственный корень – число \(5\).
- Равносильны и уравнения \(x^2+1=0\) и \(2x^2+3=1\) — ни одно из них не имеет корней.
- А вот уравнения \(x-6=0\) и \(x^2=36\) неравносильны, поскольку первое имеет только один корень \(6\), второе имеет два корня: \(6\) и \(-6\).
Равносильные преобразования уравнений — это такие преобразования, которые приводят нас к равносильным уравнениям.
Основные равносильные преобразования уравнений:
- Перенос слагаемых из одной части уравнения в другую со сменой знака слагаемого на противоположный.
Умножение или деление обеих частей уравнения на одно число или выражение не равное нулю.
Применение всех формул и свойств, которые есть в математике.
Возведение в нечетную степень обеих частей уравнения.
Извлечение корня нечетной степени из обеих частей уравнения.
Равносильные уравнения и уравнения следствия
Равносильные преобразования уравнений можно назвать «правильными» или «безошибочными» преобразованиями, потому что, сделав их, вы не нарушите математических законов. Почему тогда математики так их и не назвали: «правильные преобразования уравнений»? Потому что есть еще «полу-правильные» преобразования уравнений. В них уравнение при преобразовании приобретает дополнительные корни по ходу решения, но лишние корни мы при записи ответа не учитываем. Строгие математики их называют уравнениями следствиями:
Если каждый корень первого уравнения является корнем второго уравнения, но при этом у второго также есть корни не подходящие первому, то второе уравнение является следствием второго.
Пример (ОГЭ). Решите уравнение \(x^2-2x+\sqrt<2-x>=\sqrt<2-x>+3\)
Перенесем оба слагаемых из правой части в левую.
Взаимно уничтожим подобные слагаемые. Это и есть «полу-правильное преобразование», так как после него у уравнения становится два корня вместо изначального одного.
Это уравнение следствие из предыдущего. Найдем корни уравнения по теореме Виета .
Сверяем корни с ОДЗ и исключаем неподходящие.
\(↑\) не подходит под ОДЗ
Переходить к уравнению следствию не запрещено, но при работе с ними нужно быть осторожным и не забывать про ОДЗ .
Пример. В каких пунктах применялись равносильные преобразования, а в каких был переход к уравнению следствию? Укажите какие виды равносильных преобразований применялись.
Решение:
В пункте a) применялось равносильное преобразование 1.
В пункте b) перешли к уравнению следствию, так как \(\sqrt
В пункте с) тоже перешли к уравнению следствию, из-за того что умножили на знаменатель;
В пункте d) применялось равносильное преобразование: «Извлечения корня нечетной степени из обеих частей уравнения»;
В пункте e) умножили обе части уравнения на \(2\) т.е. равносильно преобразовали;
В пункте f) перешли от вида \(a^
Возведение обеих частей уравнения в квадрат
2. Возведение обеих частей уравнения в квадрат.
Пусть даны два уравнения 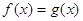
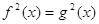
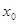
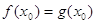
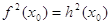
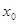
В то же время из равенства квадратов чисел не следует равенство этих чисел (числа могут быть противоположенными). Поэтому из уравнения (2) не следует уравнение (1). Отсюда вытекает, что если при решении уравнения использовалось возведение обеих частей уравнения в квадрат, то нужно повести дополнительное исследование, позволяющее исключить «посторонние» корни, если они появились.
Пример 1. Решить уравнение 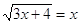
Решение. Возведем обе части этого уравнения в квадрат.
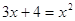
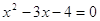
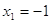
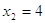
Если 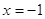
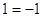
Если 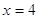
Следовательно, уравнение имеет единственный корень: 4.
3. Выполнение в одной части (или в обеих частях) уравнения тождественных преобразований, приводящих к расширению области определения равнения.
Если некоторое тождественное преобразование привело к расширению области определения уравнения, то получаем уравнения — следствие. При этом могут существовать такие значения переменной, которые являются корнями исходного уравнения.
Пример 1. Решить уравнение 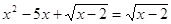
Решение. Выполнив приведение подобных слагаемых, получим: 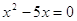
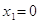
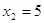
Если 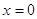
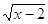
Если 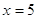
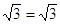
Следовательно, уравнение имеет единственный корень:5.
Пример 2. Решить уравнение 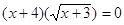
Решение. 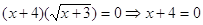
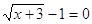
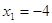
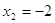
Если 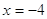
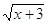
Если 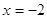
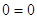
Следовательно, уравнение имеет единственный корень:-2.
Если при решении уравнения мы заменили его уравнением — следствием, то указанная выше проверка является неотъемлемой частью решения уравнения. Поэтому важно знать, при каких преобразованиях данное уравнение переходит в следствие.
Рассмотрим уравнение 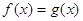
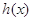
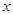
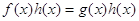
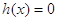
Значит, уравнение (4) есть следствие уравнения (3). Ясно, что уравнения (3) и (4) равносильны, если «постороннее» уравнение 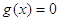
Теорема 1. Если обе части уравнения умножить на 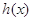
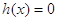
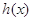
Пример 1. 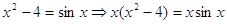
Заметим, что подобное преобразование, т.е. переход от уравнения (4) к уравнению (3) делением обеих частей уравнения (4) на выражение 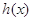
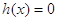
Пример 2. Уравнение 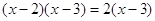
Деление обеих частей уравнения на 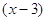
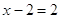
Снова возьмем уравнение (3) и возведем обе его части в квадрат. Получим уравнение: 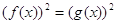
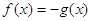
Пример 3. Уравнение 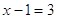
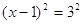
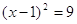
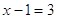
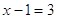
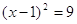
Теорема 2. При возведении обеих частей уравнения в квадрат (и вообще в любую четную степень) получается уравнение, являющееся следствием исходного.
Пример 1. 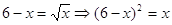
При решении иррационального уравнения чаще всего стараются заменить его более простым, но равносильным исходному. Поэтому важно знать равносильные преобразования.
Определение 10. Уравнение, имеющее одни и те же корни, называют равносильными уравнениями. Уравнения, не имеющие корней, также считают равносильными. Другими словами два уравнения называют равносильными, если множества их решений совпадают. Равносильность обозначается следующим образом: 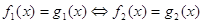
Пример 1. Уравнения 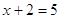
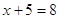
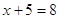
Пример 2. Уравнения 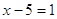
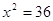
Пример 3. Уравнения 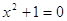
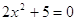
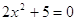
Определение 11. Пусть даны уравнения 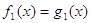
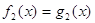
Пример 1. 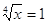
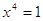
Отметим, что часто множество М совпадает либо с ОДЗ уравнения 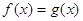
Имеется ряд теорем о равносильности уравнений.
Теорема 3. При возведении обеих частей уравнения в одну и ту же нечетную степень получается уравнение, равносильное исходному.
Пример 1. 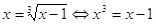
Теорема 4. Если в уравнении какое-нибудь слагаемое перенести из одной части в другую, изменив его знак, то получится уравнение, равносильное исходному.
Пример 1. 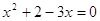
Теорема 5. Если обе части уравнения умножить или разделить на одно и тоже отличное от ноля число, то получится уравнение, равносильное исходному.
Пример 1. 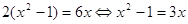
Теорема 6. Если в какой либо части уравнения выполнить тождественные преобразования, не меняющие области определения уравнения, то получится уравнение, равносильное исходному.
В школьной практике при решении иррациональных уравнений чаще всего используются два основных метода:
1) обеих частей уравнения в одну и ту же степень;
2) введение новых (вспомогательных) переменных.
Эти методы будем считать стандартными. В обязательном школьном курсе обычно этими методами и ограничиваются. Однако иногда приходится применять нестандартные методы и искусственные приемы решения иррациональных уравнений.
Типичная ошибка при решении иррациональных уравнений состоит в том, что школьники без дополнительных пояснений используют преобразования, нарушающие равносильность, что приводит к потере корней и появлению «посторонних» корней.
При возведении обеих частей иррационального уравнения в одну и ту же степень надо иметь в виду, что если степень — не четное число, то получим равносильное уравнение, если же степень — четное число, то получим уравнение — следствие. Поэтому при решении иррациональных уравнений в большинстве случаев необходима проверка найденных решений.
Проверки можно избежать, если решать иррациональные уравнения с помощью равносильных замен. Для этого полезно знать следующие теоремы.
Теорема 7. Уравнение вида 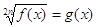
Уравнение вида
Теорема 8. Уравнение вида 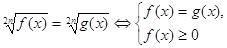
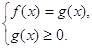
Уравнение вида 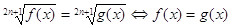
Далее рассмотрим более подробно типы иррациональных уравнений и методы их решения.
Равносильные уравнения, преобразование уравнений
Некоторые преобразования позволяют нам перейти от решаемого уравнения к равносильным, а также к уравнениям-следствиям, благодаря чему упрощается решение первоначального уравнения. В данном материале мы расскажем, что из себя представляют эти уравнения, сформулируем основные определения, проиллюстрируем их наглядными примерами и поясним, как именно осуществляется вычисление корней исходного уравнения по корням уравнения-следствия или равносильного уравнения.
Понятие равносильных уравнений
Равносильными называются такие уравнения, имеющие одни и те же корни, или же те, в которых корней нет.
Определения такого типа часто встречаются в различных учебниках. Приведем несколько примеров.
Уравнение f ( x ) = g ( x ) считается равносильным уравнению r ( x ) = s ( x ) , если у них одинаковые корни или у них обоих нет корней.
Уравнения с одинаковыми корнями считаются равносильными. Также ими считаются два уравнения, одинаково не имеющие корней.
Если уравнение f ( x ) = g ( x ) имеет то же множество корней, что и уравнение p ( x ) = h ( x ) , то они считаются равносильными по отношению друг к другу.
Когда мы говорим о совпадающем множестве корней, то имеем в виду, что если определенное число будет корнем одного уравнения, то оно подойдет в качестве решения и другому уравнению. Ни одно из уравнений, являющихся равносильными, не может иметь такого корня, который не подходит для другого.
Приведем несколько примеров таких уравнений.
Например, равносильными будут 4 · x = 8 , 2 · x = 4 и x = 2 , поскольку каждое из них имеет только один корень – двойку. Также равносильными будут x · 0 = 0 и 2 + x = x + 2 , поскольку их корнями могут быть любые числа, то есть множества их решений совпадают. Также равносильными будут уравнения x = x + 5 и x 4 = − 1 , каждое из которых не имеет ни одного решения.
Для наглядности рассмотрим несколько примеров неравносильных уравнений.
К примеру, таковыми будут x = 2 и x 2 = 4 , поскольку их корни отличаются. То же относится и к уравнениям x x = 1 и x 2 + 5 x 2 + 5 , потому что во втором решением может быть любое число, а во втором корнем не может быть 0 .
Определения, данные выше, подойдут и для уравнений с несколькими переменными, однако в том случае, когда мы говорим о двух, трех и более корнях, более уместно выражение «решение уравнения». Таким образом, подытожим: равносильные уравнения – это те уравнения, у которых одни и те же решения или их совсем нет.
Возьмем примеры уравнений, которые содержат несколько переменных и являются равносильными друг другу. Так, x 2 + y 2 + z 2 = 0 и 5 · x 2 + x 2 · y 4 · z 8 = 0 включают в себя по три переменных и имеют только одно решение, равное 0 , во всех трех случаях. А пара уравнений x + y = 5 и x · y = 1 равносильной по отношению друг к другу не будет, поскольку, например, значения 5 и 3 подойдут для первого, но не будут решением второго: при подстановке их в первое уравнение мы получим верное равенство, а во второе – неверное.
Понятие уравнений-следствий
Процитируем несколько примеров определений уравнений-следствий, взятых из учебных пособий.
Следствием уравнения f ( x ) = g ( x ) будет уравнение p ( x ) = h ( x ) при условии, что каждый корень первого уравнения будет в то же время корнем второго.
http://kazedu.com/referat/101463/1
http://zaochnik.com/spravochnik/matematika/systems/ravnosilnye-uravnenija-preobrazovanie-uravnenij/