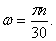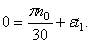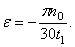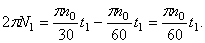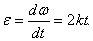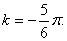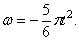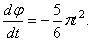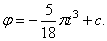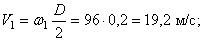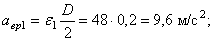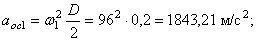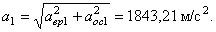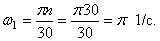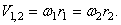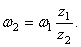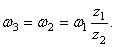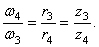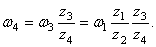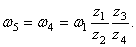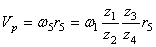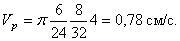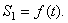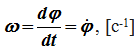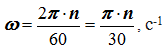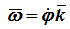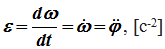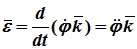Теоретическая механика:
Вращательное движение твердого тела

Смотрите также решения задач по теме «Вращательное движение» в онлайн решебниках Яблонского, Мещерского, Чертова (с примерами и методичкой для заочников), Иродова и Савельева.

При поступательном движении тела (§ 60 в учебнике Е. М. Никитина) все его точки движутся по одинаковым траекториям и в каждый данный момент они имеют равные скорости и равные ускорения.

Поэтому поступательное движение тела задают движением какой-либо одной точки, обычно движением центра тяжести.

Рассматривая в какой-либо задаче движение автомобиля (задача 147) или тепловоза (задача 141), фактически рассматриваем движение их центров тяжести.

Вращательное движение тела (Е. М. Никитин, § 61) нельзя отождествить с движением какой-либо одной его точки. Ось любого вращающегося тела (маховика дизеля, ротора электродвигателя, шпинделя станка, лопастей вентилятора и т. п.) в процессе движения занимает в пространстве относительно окружающих неподвижных тел одно и то же место.

Движение материальной точки или поступательное движение тела характеризуют в зависимости от времени линейные величины s (путь, расстояние), v (скорость) и а (ускорение) с его составляющими a_t и a_n.

Вращательное движение тела в зависимости от времени t характеризуют угловые величины : φ (угол поворота в радианах), ω (угловая скорость в рад/сек) и ε (угловое ускорение в рад/сек 2 ).

Закон вращательного движения тела выражается уравнением
φ = f (t).

Угловая скорость – величина, характеризующая быстроту вращения тела, определяется в общем случае как производная угла поворота по времени
ω = dφ/dt = f’ (t).

Угловое ускорение – величина, характеризующая быстроту изменения угловой скорости, определяется как производная угловой скорости
ε = dω/dt = f» (t).

Приступая к решению задач на вращательное движение тела, необходимо иметь в виду, что в технических расчетах и задачах, как правило, угловое перемещение выражается не в радианах φ, а в оборотах φ_об.

Поэтому необходимо уметь переходить от числа оборотов к радианному измерению углового перемещения и наоборот.

Так как один полный оборот соответствует 2π рад, то
φ = 2πφ_об и φ_об = φ/(2π).

Угловая скорость в технических расчетах очень часто измеряется в оборотах, произведенных в одну минуту (об/мин), поэтому необходимо отчетливо уяснить, что ω рад/сек и n об/мин выражают одно и то же понятие – скорость вращения тела (угловую скорость), но в различных единицах – в рад/сек или в об/мин.

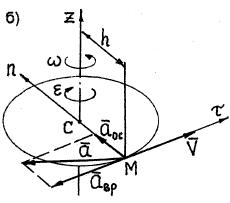
Переход от одних единиц угловой скорости к другим производится по формулам
ω = πn/30 и n = 30ω/π.

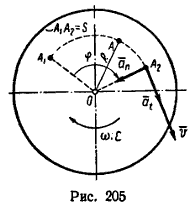
При вращательном движении тела все его точки движутся по окружностям, центры которых расположены на одной неподвижной прямой (ось вращающегося тела). Очень важно при решении задач, приведенных в этой главе, ясно представлять зависимость между угловыми величинами φ, ω и ε, характеризующими вращательное движение тела, и линейными величинами s, v, a_t и a_n, характеризующими движение различных точек этого тела (рис 205).

Если R – расстояние от геометрической оси вращающегося тела до какой-либо точки А (на рис. 205 R=OA), то зависимость между φ – углом поворота тела и s – расстоянием, пройденным точкой тела за то же время, выражается так:
s = φR.

Зависимость между угловой скоростью тела и скоростью точки в каждый данный момент выражается равенством
v = ωR.

Касательное ускорение точки зависит от углового ускорения и определяется формулой
a_t = εR.

Нормальное ускорение точки зависит от угловой скорости тела и определяется зависимостью
a_n = ω 2 R.

При решении задачи, приведенной в этой главе, необходимо ясно понимать, что вращением называется движение твердого тела, а не точки. Отдельно взятая материальная точка не вращается, а движется по окружности – совершает криволинейное движение.

§ 33. Равномерное вращательное движение

Если угловая скорость ω=const, то вращательное движение называется равномерным.

Уравнение равномерного вращения имеет вид
φ = φ₀ + ωt.

В частном случае, когда начальный угол поворота φ₀=0,
φ = ωt.

Угловую скорость равномерно вращающегося тела
ω = φ/t
можно выразить и так:
ω = 2π/T,
где T – период вращения тела; φ=2π – угол поворота за один период.

§ 34. Равнопеременное вращательное движение

Вращательное движение с переменной угловой скоростью называется неравномерным (см. ниже § 35). Если же угловое ускорение ε=const, то вращательное движение называется равнопеременным . Таким образом, равнопеременное вращение тела – частный случай неравномерного вращательного движения.

Уравнение равнопеременного вращения
(1) φ = φ₀ + ω₀t + εt 2 /2
и уравнение, выражающее угловую скорость тела в любой момент времени,
(2) ω = ω₀ + εt
представляют совокупность основных формул вращательного равнопеременного движения тела.

В эти формулы входят всего шесть величин: три постоянных для данной задачи φ₀, ω₀ и ε и три переменных φ, ω и t. Следовательно, в условии каждой задачи на равнопеременное вращение должно содержаться не менее четырех заданных величин.

Для удобства решения некоторых задач из уравнений (1) и (2) можно получить еще две вспомогательные формулы.

Исключим из (1) и (2) угловое ускорение ε:
(3) φ = φ₀ + (ω + ω₀)t/2.

Исключим из (1) и (2) время t:
(4) φ = φ₀ + (ω 2 — ω₀ 2 )/(2ε).

В частном случае равноускоренного вращения, начавшегося из состояния покоя, φ₀=0 и ω₀=0. Поэтому приведенные выше основные и вспомогательные формулы принимают такой вид:
(5) φ = εt 2 /2;
(6) ω = εt;
(7) φ = ωt/2;
(8) φ = ω 2 /(2ε).

§ 35. Неравномерное вращательное движение

Рассмотрим пример решения задачи, в которой задано неравномерное вращательное движение тела.

Вращательное движение твердого тела задано уравнением

МЕТОДИЧЕСКИЕ УКАЗАНИЯ И ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ПО КИНЕМАТИКЕ

Кинематика вращения тела вокруг неподвижной оси

1. Краткие сведения из теории

Уравнение вращательного движения твердого тела вокруг неподвижной оси имеет вид

. (40)

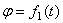
Отсчет угла ведется от выбранного начала. При этом углам, отложенным в направлении движения часовой стрелки, придается знак “минус”, а углам противоположного направления – знак “плюс”.

Угол поворота выражается в радианах. Иногда угол поворота определяется числом оборотов N. Зависимость между и N следующая .

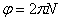
Угловая скорость тела:

(41)

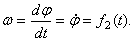
Знак производной 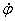дает возможность установить происходит ли вращение тела в положительном направлении отсчета угла поворота (знак “плюс”) или в обратную сторону (знак “минус”). Единица измерения угловой скорости – радиан в секунду (или 1/с).

Иногда угловую скорость характеризуют числом оборотов в минуту и обозначают буквой n . Зависимость между и n имеет вид

Угловое ускорение тела:

(42)

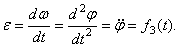
Знак производной 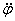дает возможность установить является ли вращение тела в данный момент времени ускоренным или замедленным. Если знаки и одинаковы, тело вращается ускоренно, а если их знаки различны – замедленно. Единица измерения углового ускорения – радиан на секунду в квадрате (или 1/с 2 ).

Траекториями точек тела, не лежащих на оси вращения, являются окружности с центрами на оси вращения и радиусами, равными кратчайшему расстоянию от этих точек до оси вращения.

Модуль скорости любой точки тела, находящейся на расстоянии h от оси вращения (рис. 18), определяется по формуле

. (43)

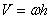
Направлена скорость точки по касательной к описываемой точкой окружности в сторону движения.

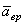
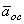
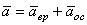
Ускорение любой точки тела состоит из двух составляющих – вращательного и осестремительного ускорений:

.

Модуль вращательного ускорения точки определяется по формуле

. (44)

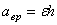
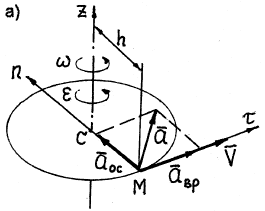
Вращательное ускорение направлено по касательной к описываемой точкой окружности в ту же сторону, что и его скорость, если вращение тела ускоренное (рис. 18, а) и в сторону, противоположную скорости, если вращение замедленное (рис.18, б).

Модуль осестремительного ускорения определяется по формуле

. (45)

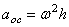
Осестремительное ускорение всегда направлено по радиусу окружности от точки к центру окружности (рис. 18).

Модуль полного ускорения точки определяется по формуле

(46)

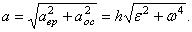
2. Основные типы задач кинематики вращения тела вокруг оси

В зависимости от того, что задано в условии задачи и что требуется определить, различают следующие два основных типа задач.

1. Исследуется движение тела в целом. В этих задачах вначале нужно получить законы (40)–(42) и, используя связь между ними, определить требуемую величину (см. примеры 17 и 18).

2. Требуется определить скорости и ускорения отдельных точек тела. Для решения задач этого типа вначале надо установить кинематические характеристики движения всего тела в целом, т.е. найти , и . После чего по формулам (43), (44), (45), (46) определить скорости и ускорения точек тела (см. пример 19).

Пример 17. Пропеллер самолета, делающий 1200 об / мин , после выключения двигателя останавливается через 8 с. Сколько оборотов сделал пропеллер за это время, если считать его вращение равнозамедленным?

Вначале получим законы вращения пропеллера (40), (41) и (42). По условию задачи пропеллер вращается равнозамедленно , из этого следует, что

.

, (47)

(48)

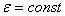
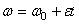
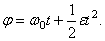
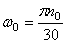
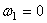
Начальной угловой скоростью при замедленном вращении будет та, которую пропеллер имел до выключения двигателя. Следовательно, . В момент остановки при t₁ = 8 сек. угловая скорость тела . Подставляя эти значения в уравнение (47), получим

Отсюда

Если обозначить число сделанных пропеллером за время t₁ оборотов через N₁, то угол поворота за то же время будет равен

.

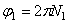
Подставляя найденные значения и в уравнение (48), получим

Отсюда оборотов.

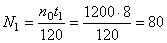
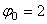
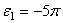
Пример 18. Найти закон вращения тела вокруг оси, если известны следующие данные: угловая скорость изменяется пропорционально t 2 , начальный угол поворота рад, для заданного момента времени t₁ = 3 с угловое ускорение 1/с 2 .

По условию задачи модуль угловой скорости изменяется пропорционально t 2 . Обозначая неизвестный коэффициент пропорциональности буквой k , имеем

. (49)

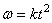
Найдем , беря производные по времени от обеих частей равенства (49),

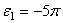
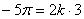
Определим коэффициент k из условия, что при t₁ = 3 сек. угловое ускорение 1/с 2 : или

Подставляя значение k в уравнение (49), получим

Учитывая, что 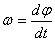, будем иметь

Умножая обе части этого уравнения на dt и интегрируя, находим

В начальный момент при t = 0, 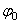= 2 рад, следовательно, c = 2.

Таким образом, 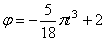радиан.

Пример 19. В период разгона ротор электродвигателя вращается по закону 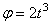, где t в сек, в рад.

Определить в конце 4-й секунды линейную скорость, вращательное, осестремительное и полное ускорения точки, лежащей на ободе ротора, если диаметр ротора D = 40 см .

По заданному уравнению вращения ротора находим его угловую скорость и угловое ускорение , .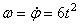

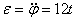
Подставляя значение t₁ = 4 сек в выражение для и , найдем

1/с,

1/с 2 .

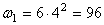
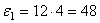
Определим модули линейной скорости, вращательного и осестремительного ускорений в этот же момент времени по формулам (43), (44) и (45)

Модуль полного ускорения точки обода ротора определим по формуле (46)

3. Определение скоростей и ускорений в случаях, когда вращающееся тело входит в состав различных механизмов

Рассмотрим механизмы с поступательным и вращательным движением звеньев. Решение задачи начинают с определения скоростей точек того звена, для которого движение задано. Затем рассматривают звено, которое присоединено к первому звену и т.д. В результате определяют скорости точек всех звеньев механизма. В такой же последовательности определяют и ускорения точек.

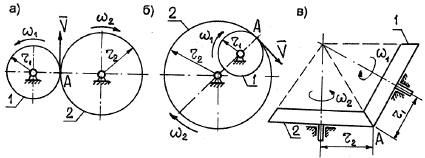
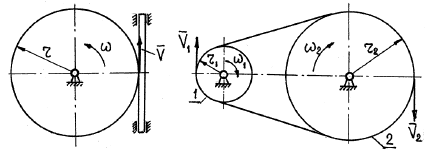
Передача вращения от одного вращающегося тела, называемого ведущим, к другому, называемому ведомым, может осуществляться при помощи фрикционной или зубчатой передачи (рис. 19).

Во фрикционной передаче вращение передается вследствие действия силы трения в месте контакта соприкасающихся колес, в зубчатой передаче – от зацепления зубьев. Оси вращения ведущего и ведомого колес могут быть параллельными (рис. 19, а, б) или пересекаться (рис. 19, в). В рассмотренных случаях линейные скорости точек А соприкасания колес одинаковы, их модули определяются так:

. (50)

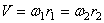
Отсюда 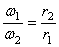. (51)

То есть угловые скорости колес фрикционной или зубчатой передачи обратно пропорциональны радиусам колес.

При преобразовании вращательного движения в поступательное (или наоборот) часто используют зацепление зубчатого колеса с зубчатой рейкой (рис. 20). Для этой передачи выполняется условие: .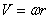

Кроме фрикционной и зубчатой передач, существует передача вращения при помощи гибкой связи (ремня, троса, цепи) (рис. 21).

Так как модули скоростей всех точек ремня одинаковы и ремень не скользит по поверхностям шкивов, то соотношения (50) и (51) относятся и к ременной передаче.

Пример 20. В механизме домкрата при вращении рукоятки ОА шестерни 1, 2, 3, 4, 5 приводят в движение зубчатую рейку ВС домкрата (рис. 22).

Определить скорость рейки, если рукоятка ОА делает 30 оборотов в минуту ( n = 30 об /мин). Числа зубцов шестерен: z₁ = 6, z₂ = 24, z₃ = 8, z₄ = 32; радиус пятой шестерни r₅ = 4 см .

Так как рукоятка ОА жестко соединена с шестерней 1, то последняя делает тоже 30 об /мин или

Модули скоростей точек соприкасания зубчатых колес 1 и 2 одинаковы для точек обоих колес и определяются по формуле (50)

Отсюда 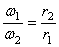(см. также (51)).

Так как числа зубьев пропорциональны радиусам колес, то .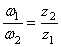

Отсюда

Шестерни 2 и 3 жестко соединены между собой, поэтому

Для находящихся в зацеплении колес 3 и 4 на основании (51) можно записать

Отсюда

Шестерни 4 и 5 жестко соединены между собой, поэтому

Модули скоростей точек соприкосновения зубчатой рейки ВС и шестерни 5 одинаковы, поэтому

или

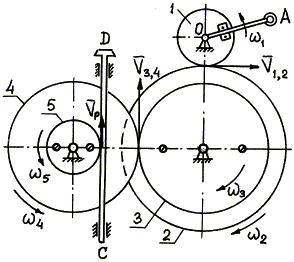
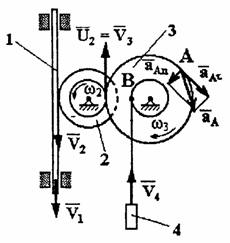
Пример 21. Рейка 1, ступенчатое колесо 2 с радиусами R ₂ и r ₂ и колесо 3 радиуса R ₃ , скрепленное с валом радиуса r₃, находятся в зацеплении; на вал намотана нить с грузом 4 на конце (рис.23). Рейка движется по закону

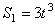
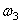
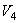
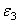
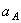
Дано: R ₂ =6 см, r₂=4 см, R₃=8 см, r₃=3 см, ( S — в сантиметрах, t — в секундах), А — точка обода колеса 3, t ₁ =3 с. Определить: , , , в момент времени t = t₁.

Указания. Пример 21 — на исследование вращательного движения твердого тела вокруг неподвижной оси. При решении задачи учесть, что, когда два колеса находятся в зацеплении, скорость точки зацепления каждого колеса одна и та же, а когда два колеса связаны передачей, то скорости всех точек ремня и, следовательно, точек, лежащих на ободе каждого из этих колес, в данный момент времени численно одинаковы, при этом считается, что ремень по ободу колес не скользит.

Условимся обозначать скорости точек, лежащих на внешних ободах колес (радиуса R ₁ ), через V₁, а точек, лежащих на внутренних ободах (радиуса r ₁ ), через U₁.

1. Зная закон движения рейки 1, находим ее скорость:

. ( 52 )

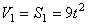
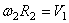
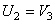
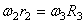
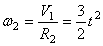
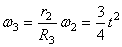
Так как рейка и колесо 2 находятся в зацеплении, то V ₂ = V₁ или . Но колеса 2 и 3 тоже находятся в зацеплении, следовательно, или . Из этих равенств находим:

, . (53)

Тогда для момента времени t₁ = 3 сек. получим 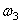= 6,75 с -1 .

2. Определяем V ₄ . Так как 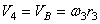, то при t₁=3 c ек . V ₄ = 20 ,25 см/с.

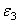
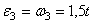
3. Определяем . Учитывая второе из равенств (53), получим .

Тогда при t₁ = 3 сек. 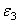= 4,5 с -2 .

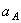
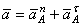
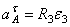
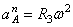
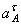
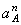
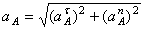
4. Определяем . Для точки А , где численно , . Тогда для момента времени t₁ = 3 сек. имеем = 36 см/с2, = 364,5 см/с2.

= 366,3 см/с 2 ,

Все скорости и ускорения точек, а также направления угловых скоростей показаны на рис.2.

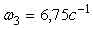
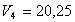
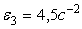
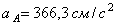
Ответ: , см/ с , , .

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

iSopromat.ru

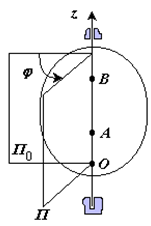
Вращательное движение твердого тела – это движение, при котором тело имеет как минимум две неподвижные точки (рисунок 1.3). Прямая, проходящая через эти точки, называется осью вращения.

Положение тела определено, если задан угол φ между плоскостями П₀ и П, одна из которых неподвижна, а другая жестко связана с телом.

φ=φ(t) – уравнение вращательного движения твердого тела.

За положительное направление отсчета принимается вращение против хода часовой стрелки, если смотреть навстречу положительному направлению оси z.

Траекториями точек тела при его вращении вокруг неподвижной оси являются окружности, расположенные в плоскостях, перпендикулярных оси вращения.

Для характеристики изменения угла поворота с течением времени вводится величина, называемая угловой скоростью ω:

В технике угловая скорость – это частота вращения, выраженная в оборотах в минуту. За одну минуту тело повернется на угол 2 π ⋅ n , где n – число оборотов в минуту (об/мин). Разделив этот угол на число секунд в минуте, получим

Вектор угловой скорости – это вектор, направленный по оси вращения в ту сторону, откуда вращение видно происходящим против хода часовой стрелки, с модулем, равным модулю алгебраической угловой скорости

где k – единичный вектор оси вращения.

Угловое ускорение – мера изменения угловой скорости:

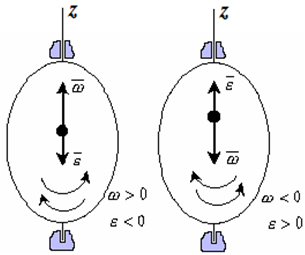
Вектор углового ускорения – производная вектора угловой скорости по времени (рис. 1.4)

1. Если ε >0 и ω >0 (рисунок 1.4), то угловая скорость возрастает с течением времени и, следовательно, тело вращается ускоренно в рассматриваемый момент времени в положительную сторону. Направление векторов ω и ε совпадают, оба они направлены в положительную сторону оси вращения Oz.
2. При ε ω – тело вращается ускоренно в отрицательную сторону. Направление векторов ω и ε совпадают, оба они направлены в отрицательную сторону оси вращения Oz.
3. Если ε ω >0 , то имеем замедленное вращение в положительную сторону. Векторы ω и ε направлены в противоположные стороны.
4. Если ε >0 при
   ω , то имеем замедленное вращение в отрицательную сторону. Векторы ω и ε направлены в противоположные стороны.
5. Если угловая скорость ω=const , то вращательное движение называется равномерным. Уравнение равномерного вращения

Если угловое ускорение ε=const, то вращательное движение называется равнопеременным.
Уравнение равнопеременного вращения 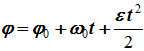и уравнение, выражающее угловую скорость в любой момент времени

представляют совокупность основных формул вращательного равнопеременного движения тела.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах