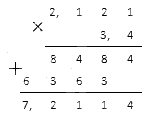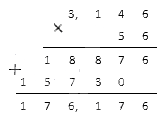Все действия с рациональными числами уравнения

Действия с рациональными числами: правила, примеры, решения

Ниже рассмотрим правила основных математических действий над рациональными числами: сложение, вычитание, умножение и деление. Разберем теорию на практических примерах.

Действие сложения рациональных чисел

Рациональные числа содержат натуральные, тогда смысл действия сложения рациональных чисел сопоставим со смыслом сложения натуральных. Например, сумму рациональных чисел, записанную как 5 + 1 4 возможно описать следующим образом: к 5 целым предметам добавили четверть такого предмета, после чего полученное количество рассматривается совместно.

Сформулируем правила сложения рациональных чисел:

Сложение нуля с отличным от него рациональным числом

Прибавление нуля к любому числу дает то же число. Данное правило возможно записать в виде равенства: a + 0 = a (для любого рационального числа а). Используя переместительное свойство сложения, получим также верное равенство: 0 + a = a .

Пара простых примеров: сумма рационального числа 2 , 1 и числа 0 равно 2 , 1 и: 6 4 5 + 0 = 6 4 5 .

Сложение противоположных рациональных чисел

Сумма противоположных чисел равна нулю.

Данное правило можно записать в виде: a + ( — a ) = 0 (для любого рационального числа a ).

К примеру, числа 45 , 13 и — 45 , 13 являются противоположными, т.е. их сумма равно нулю: 45 , 13 + ( — 45 , 13 ) = 0 .

Сложение положительных рациональных чисел

В виде обыкновенной дроби возможно представить любое положительное рациональное число и использовать далее схему сложения обыкновенных дробей.

Необходимо произвести сложение рациональных чисел: 0 , 6 и 5 9 .

Решение

Выполним перевод десятичной дроби в обыкновенную и тогда: 0 , 6 + 5 9 = 6 10 + 5 9 .

Осуществим сложение дробей с разными знаменателями:

6 10 + 5 9 = 54 90 + 50 90 = 104 90 = 1 7 45

Ответ: 0 , 6 + 5 9 = 1 7 45 .

Рациональные числа, которые подвергают действию сложения, возможно записать в виде конечных десятичных дробей или в виде смешанных чисел и, таким образом, осуществить сложение десятичных дробей и смешанных чисел соответственно.

Сложение рациональных чисел с разными знаками

Для того, чтобы осуществить сложение рациональных чисел с разными знаками, необходимо из бОльшего модуля слагаемых вычесть меньший и перед полученным результатом поставить знак того числа, модуль которого больше.

Необходимо осуществить сложение рациональных чисел с разными знаками 8 , 2 и — 2 3 4 .

Решение

Согласно исходным данным, необходимо произвести сложение положительного числа с отрицательным. Придерживаясь вышеуказанного правила, определим модули заданных чисел: | 8 , 2 | = 8 , 2 и | — 2 3 4 | = 2 3 4 . Проведя сравнение модулей — рациональных чисел, получим: 8 , 2 > 2 3 4 и соответственно поймем, какое число из заданных станет уменьшаемым, а какое — вычитаемым. Произведем вычитание смешанных чисел, т.е.: 8 , 2 — 2 3 4 = 8 2 10 — 2 3 4 = 5 9 20 .

Полученному результату присваивается знак плюс, т.к. бОльшее из слагаемых по модулю – положительное число. Ответ: 8 , 2 + ( — 2 3 4 ) = 5 9 20 .

Сложение отрицательных рациональных чисел

Для того, чтобы произвести сложение отрицательных рациональных чисел, необходимо сложить модули заданных слагаемых, затем полученному результату присвоить знак минус.

Необходимо произвести сложение чисел: — 4 , 0203 и — 12 , 193 .

Решение

Модули заданных чисел соответственно равны: 4 , 0203 и 12 , 193 . Сложим их:

​​​​​​

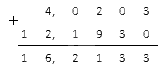
Полученному результату присваиваем знак минус: — 16 , 2133 .

Ответ: ( — 4 , 0203 ) + ( — 12 , 193 ) = — 16 , 2133 .

Действие вычитания рациональных чисел

Вычитание – действие, обратное сложению, в котором мы находим неизвестное слагаемое по сумме и известному слагаемому. Тогда из равенства c + b = a следует, что a — b = c и a — c = b . И наоборот: из равенств a — b = c и a — c = b следует, что c + b = a .

При вычитании из бОльшего положительного рационального числа мы либо производим вычитание обыкновенных дробей, либо, если это уместно, вычитание десятичных дробей или смешанных.

Необходимо вычислить разность рациональных чисел: 4 , ( 36 ) – 1 5 .

Решение

Сначала переведем периодическую десятичную дробь в обыкновенную: 4 , ( 36 ) = 4 + ( 0 , 36 + 0 , 0036 + … ) = 4 + 0 , 36 1 — 0 , 01 = 4 + 36 99 = 4 + 4 11 = 4 4 11

Далее переходим к действию вычитания обыкновенной дроби из смешанного числа: 4 , ( 36 ) — 1 5 = 4 4 11 — 1 5 = 4 + 4 11 — 1 5 = 4 + 20 55 — 11 55 = 4 + 9 55 = 4 9 55

Ответ: 4 , ( 36 ) — 1 5 = 4 9 55

В прочих случаях вычитание рациональных чисел необходимо заменить сложением: к уменьшаемому прибавить число, противоположное вычитаемому: a – b = a + ( — b ) .

Указанное равенство можно доказать, опираясь на свойства действий с рациональными числами. Они дают возможность записать цепочку равенств: ( a + ( — b ) ) + b = a + ( ( — b ) + b ) = a + 0 = a . Отсюда в силу смысла действия вычитания следует, что сумма a + ( — b ) есть разность чисел a и b .

Необходимо из рационального числа 2 7 вычесть рациональное число 5 3 7

Решение

Согласно последнему указанному правилу используем для дальнейших действий число, противоположное вычитаемому, т.е. — 5 3 7 . Тогда: 2 7 — 5 3 7 = 2 7 + — 5 3 7

Далее произведем сложение рациональных чисел с разными знаками: 2 7 + — 5 3 7 = — 5 3 7 — 2 7 = — 5 3 7 — 2 7 = — 5 1 7

Ответ: 2 7 + — 5 3 7 = — 5 1 7

Действие умножения рациональных чисел

Общее понятие числа расширяется от натуральных чисел к целым, так же как от целых к рациональным. Все действия с целыми числами имеют те же свойства, что и действия с натуральными. В таком случае, и действия с рациональными числами также должны характеризоваться всеми свойствами действий с целыми числами. Но для действия умножения рациональных чисел присуще дополнительное свойство: свойство умножения взаимообратных чисел. Вышесказанному соответствуют все правила умножения рациональных чисел. Укажем их.

Умножение на нуль

Произведение любого рационального числа a на нуль есть нуль.

Используя переместительное свойство умножения, получим: 0 · а = 0 .

К примеру, умножение рационального числа 7 13 на 0 даст 0 . Перемножив отрицательное рациональное число — 7 1 8 и нуль, также получим нуль. В частном случае, произведение нуля на нуль есть нуль: 0 · 0 = 0 .

Умножение на единицу

Умножение любого рационального числа a на 1 дает число a .

Т.е. a · 1 = a или 1 · a = a (для любого рационального a ). Единица здесь является нейтральным числом по умножению.

К примеру, умножение рационального числа 5 , 46 на 1 даст в итоге число 5 , 46 .

Умножение взаимообратных чисел

Если множители есть взаимообратные числа, то результатом их произведения будет единица. Т.е. : а · а — 1 = 1 .

К примеру, результатом произведения чисел 5 6 и 6 5 будет единица.

Умножение положительных рациональных чисел

В общих случаях умножение положительных рациональных чисел сводится к умножению обыкновенных дробей. Первым действием множители представляются в виде обыкновенных дробей, если заданные числа таковыми не являются.

Необходимо вычислить произведение положительных рациональных чисел 0 , 5 и 6 25 .

Решение

Представим заданную десятичную дробь в виде обыкновенной 0 , 5 = 5 10 = 1 2 .

Далее произведем умножение обыкновенных дробей: 1 2 · 6 25 = 6 50 = 3 25 .

Ответ: 0 , 5 · 6 25 = 3 25

Можно также работать и с конечными десятичными дробями. Удобнее будет в данном случае не переходить к действиям над обыкновенными дробями.

Необходимо вычислить произведение рациональных чисел 2 , 121 и 3 , 4 .

Решение

Перемножим десятичные дроби столбиком:

Ответ: 2 , 121 · 3 , 4 = 7 , 2114

В частных случаях нахождение произведения рациональных чисел представляет собой умножение натуральных чисел, умножение натурального числа на обыкновенную или десятичную дробь.

Умножение рациональных чисел с разными знаками

Чтобы найти произведение рациональных чисел с разными знаками, необходимо перемножить модули множителей и полученному результату присвоить знак минус.

Необходимо найти произведение чисел: — 3 3 8 и 2 1 2

Решение

Согласно вышеуказанному правилу получим: — 3 3 8 · 2 1 2 = — 3 3 8 · 2 1 2 = — 3 3 8 · 2 1 2

Заменим смешанные дроби неправильными и найдем искомое произведение: — 3 3 8 · 2 1 2 = — 27 8 · 5 2 = — 135 16 = — 8 7 16

Ответ: — 3 3 8 · 2 1 2 = — 8 7 16

Умножение отрицательных рациональных чисел

Для того, чтобы найти произведение отрицательных рациональных чисел, необходимо перемножить модули множителей.

Необходимо найти произведение отрицательных рациональных чисел — 3 , 146 и — 56 .

Решение: модули заданных чисел соответственно равны 3 , 146 и 56 .

Перемножим их столбиком:

Полученный результат и будет являться искомым произведением.

Ответ: ( — 3 , 146 ) · ( — 56 ) = 176 , 176

Деление рациональных чисел

Деление – действие, обратно умножению, в ходе которого мы находим неизвестный множитель по заданному произведению и известному множителю. Смысл действия деления можно записать так: из равенства b · c = a следует, что a : b = c и a : c = b . И наоборот: из равенств a : b = c и a : c = b следует, что b · c = a .

На множестве рациональных чисел деление не считается самостоятельным действием, поскольку оно производится через действие умножения. Собственно, этот смысл заложен в правило деления рациональных чисел.

Разделить число а на число b , отличное от нуля – то же самое, что умножить число a на число, обратное делителю. Т.е., на множестве рациональных чисел верно равенство: a : b = a · b — 1 .

Указанное равенство доказывается просто: на основе свойств действий с рациональными числами справедливой будет цепочка равенств ( a · b — 1 ) · b = a · ( b — 1 · b ) = a · 1 = a , которая и доказывает равенство a : b = a · b — 1 .

Таким образом, деление рационального числа на другое рациональное число, отличное от нуля, сводится к действию умножения рациональных чисел.

Необходимо выполнить действие деления 3 1 3 : — 1 1 6

Решение

Определим число, обратное заданному делителю. Запишем заданный делитель в виде неправильной дроби: — 1 1 6 = — 7 6 .

Число, обратное этой дроби, будет: — 6 7 . Теперь, согласно вышеуказанному правилу, произведем действие умножения рациональных чисел: 3 1 3 — 1 1 6 = 3 1 3 · — 6 7 = 10 3 · ( — 6 7 ) = — ( 10 3 · 6 7 ) = — 20 7 = — 2 6 7

Ответ: 3 1 3 : — 1 1 6 = — 2 6 7

Рациональные уравнения с примерами решения

Содержание:

Рациональные уравнения. Равносильные уравнения

два уравнения называют равносильными, если они имеют одни и те же корни. Равносильными считают и те уравнения, которые корней не имеют.

Так, например, равносильными будут уравнения

Уравнения — не равносильны, так как корнем первого уравнения является число 10, а корнем второго — число 9.

Ранее, в 7 классе, вы знакомились со свойствами, которые преобразуют уравнения в равносильные им уравнения.

1) Если в любой части уравнения раскрыть скобки или привести подобные слагаемые, то получим уравнение, равносильное данному;

2) если в уравнении перенести слагаемое из одной части в другую, изменив его знак на противоположный, то получим уравнение, равносильное данному;

3) если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получим уравнение, равносильное данному.

Левая и правая части каждого из них являются рациональными выражениями.

Уравнении, левая и правая части которых являются рациональными выражениями, называют рациональными уравнениями.

В первых двух из записанных выше уравнений левая и правая части являются целыми выражениями. Такие уравнения называют целыми рациональными уравнениями. Если хотя бы одна часть уравнения — дробное выражение, то его называют дробным рациональным уравнением. Третье из записанных выше уравнений является дробным рациональным.

Как решать целые рациональные уравнения, мы рассмотрели при изучении математики в предыдущих классах. Рассмотрим теперь, как решать дробные рациональные уравнения, то есть уравнения с переменной в знаменателе.

Применение условия равенства дроби нулю

Напомним, что когда

Пример №202

Решите уравнение

Решение:

С помощью тождественных преобразований и свойств уравнений приведем уравнение к виду где и — целые рациональные выражения. Имеем:

Окончательно получим уравнение:

Чтобы дробь равнялась нулю, нужно, чтобы числитель равнялся нулю, а знаменатель не равнялся нулю.

Тогда откуда При знаменатель Следовательно, — единственный корень уравнения.

Решение последнего, равносильного данному, уравнения, учитывая условие равенства дроби нулю, удобно записывать так:

Значит, решая дробное рациональное уравнение, можно:

1) с помощью тождественных преобразований привести уравнение к виду

2) приравнять числитель к нулю и решить полученное целое уравнение;

3) исключить из его корней те, при которых знаменатель равен нулю, и записать ответ.

Использование основного свойства пропорции

Если то где

Пример №203

Решите уравнение

Решение:

Найдем область допустимых значений (ОДЗ) переменной в уравнении. Так как знаменатели дробей не могут равняться нулю, то Имеем: то есть ОДЗ переменной содержит все числа, кроме 1 и 2.

Сложив выражения в правой части уравнения, приведем его к виду: получив пропорцию:

По основному свойству пропорции имеем:

Решим это уравнение:

откуда

Так как число 4 принадлежит ОДЗ переменной исходного уравнения, то 4 является его корнем.

Запись решения, чтобы не забыть учесть ОДЗ, удобно закончить так:

Таким образом, для решения дробного рационального уравнения можно:

1) найти область допустимых значений (ОДЗ) переменной в уравнении;

2) привести уравнение к виду

3) записать целое уравнение и решить его;

4) исключить из полученных корней те, которые не принадлежат ОДЗ, и записать ответ.

Метод умножения обеих частей уравнения на общий знаменатель дробей

Пример №204

Решите уравнение

Решение:

Найдем ОДЗ переменной и простейший общий знаменатель всех дробей уравнения, разложив знаменатели на множители:

Областью допустимых значений переменной будут те значения при которых то есть все значения кроме чисел А простейшим общим знаменателем будет выражение

Умножим обе части уравнения на это выражение:

Получим: а после упрощения: то есть откуда или

Число 0 не принадлежит ОДЗ переменной исходного уравнения, поэтому не является его корнем.

Следовательно, число 12 — единственный корень уравнения. Ответ. 12.

Решая дробное рациональное уравнение, можно:

3) умножить обе части уравнения на этот общий знаменатель;

4) решить полученное целое уравнение;

5) исключить из его корней те, которые не принадлежат ОДЗ переменной уравнения, и записать ответ.

Пример №205

Являются ли равносильными уравнения

Решение:

Поскольку уравнения являются равносильными в случае, когда они имеют одни и те же, или не имеют корней, найдем корни данных уравнений.

Первое уравнение имеет единственный корень а второе — два корня (решите уравнения самостоятельно). Следовательно, уравнения не являются равносильными.

Степень с целым показателем

Напомним, что в 7 классе мы изучали степень с натуральным показателем. По определению:

где — натуральное число,

В математике, а также при решении задач практического содержания, например в физике или химии, встречаются степени, показатель которых равен нулю или является целым отрицательным числом. Степень с отрицательным показателем можно встретить и в научной или справочной литературе. Например, массу атома гелия записывают так: кг. Как понимать смысл записи

Рассмотрим степени числа 3 с показателями — это соответственно

В этой строке каждое следующее число втрое больше предыдущего. Продолжим строку в противоположном направлении, уменьшая каждый раз показатель степени на 1. Получим:

Число должно быть втрое меньше числа равного числу 3. Но втрое меньшим числа 3 является число 1, следовательно, Равенство справедливо для любого основания при условии, что

Нулевая степень отличного от нуля числа а равна единице, то есть при

Вернемся к строке со степенями числа 3, где слева от числа записано число Это число втрое меньше, чем 1, то есть равно Следовательно, Рассуждая аналогично получаем: и т. д.

Приходим к следующему определению степени с целым отрицательным показателем:

если натуральное число, то

Рациональные уравнения онлайн калькулятор

Наш калькулятор поможет вам решить рациональное уравнение или неравенство. Искусственный интеллект, который лежит в основе калькулятора, даст ответ с подробным решением и пояснениями.

Калькулятор полезен старшеклассникам при подготовке к контрольным работам и экзаменам, для проверки знаний перед ЕГЭ, родителям школьников с целью контроля решения многих задач по математике и алгебре.

Добро пожаловать на сайт Pocket Teacher

Наш искусственный интеллект решает сложные математические задания за секунды

Мы решим вам контрольные, домашние задания, олимпиадные задачи с подробными шагами. Останется только переписать в тетрадь!

начать

Рациональные уравнения

В рациональных уравнениях обе части уравнения представляют собой рациональные выражения вида: s(x) = 0 или расширено: s(x) = b(x), где s(x), b(x) – рациональные выражения.

Рациональное выражение является алгебраическим выражением, которое состоит из рациональных чисел и переменной величины, соединенных с помощью сложения, вычитания, умножения, деления и возведения в степень с натуральным показателем. Таким образом, это целые и дробные выражения без радикалов.

Действия с рациональными числами обладают свойствами действий с целыми числами.

К примеру, при умножении рациональных чисел есть дополнительное свойство – умножение взаимно обратных чисел. Для того чтобы умножить два рациональных числа, необходимо умножить модули этих чисел, а перед ответом поставить «плюс», если у множителей одинаковые знаки и «минус», если знаки разные.

Умножение рационального числа на ноль. Когда в рациональном уравнении хоть один множитель – ноль, то и произведение будет равняться нолю.

Умножение рациональных чисел с разными знаками. При умножении нескольких чисел с разными знаками, необходимо умножить модули каждого из этих чисел. Если количество множителей с отрицательными знаками – четное, то произведение всегда будет со знаком «плюс», если количество множителей с отрицательными знаками – нечетное, то и произведение будет со знаком «минус».

Делить на ноль в рациональных уравнениях, как и в обычных нельзя.

Чтобы решить рациональное уравнение, необходимо определить тип этого уравнения и применить некоторые математические хитрости, созданные для этого типа. Если Вы не помните этих хитростей, то можете воспользоваться калькулятором для решения рациональных уравнений, который быстро подберёт все корни данного уравнений.

Решением рационального уравнения будут являться корень – конкретное число, при постановке которого в уравнение даст верное равенство. Корней рационального уравнения может быть много и важно в решении не упустить ни один корень.

Бесплатный онлайн калькулятор

Наш бесплатный решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в калькуляторе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей группе ВКонтакте: pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.

Наш искусственный интеллект решает сложные математические задания за секунды.

Мы решим вам контрольные, домашние задания, олимпиадные задачи с подробными шагами. Останется только переписать в тетрадь!