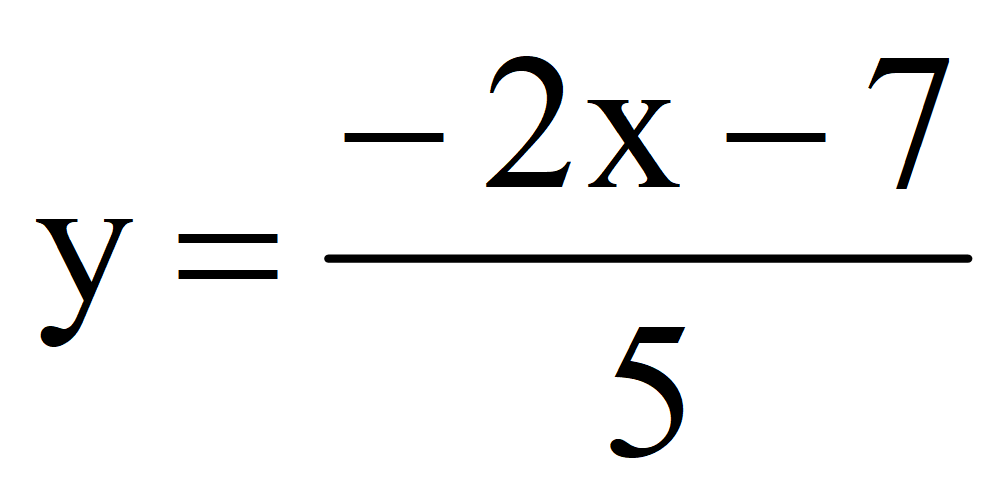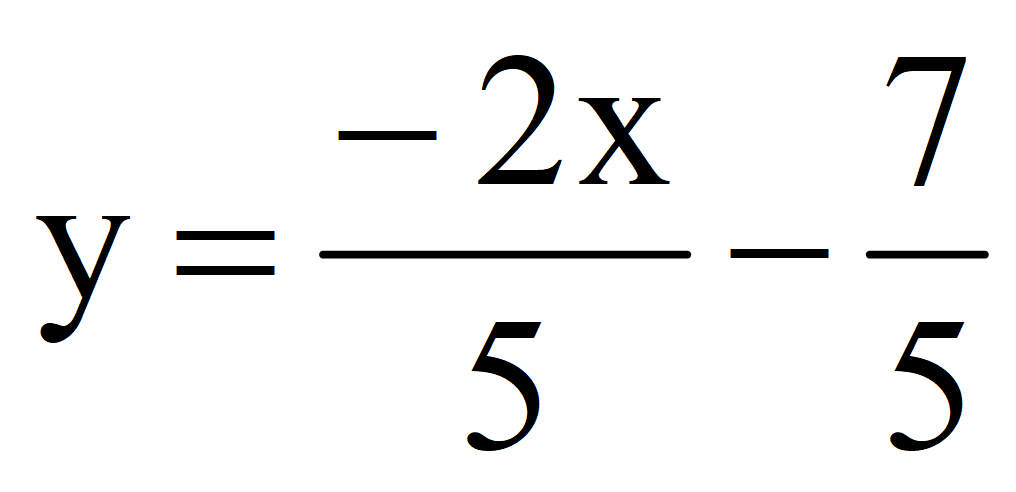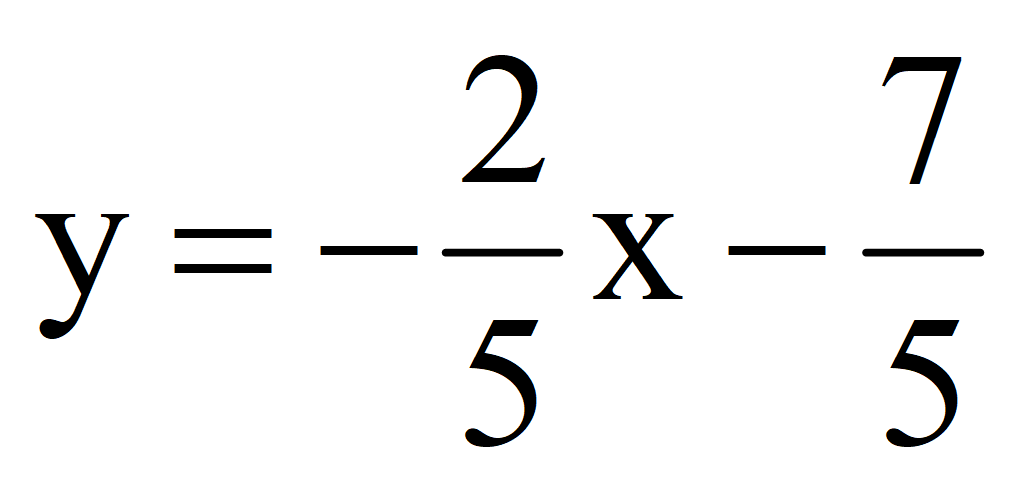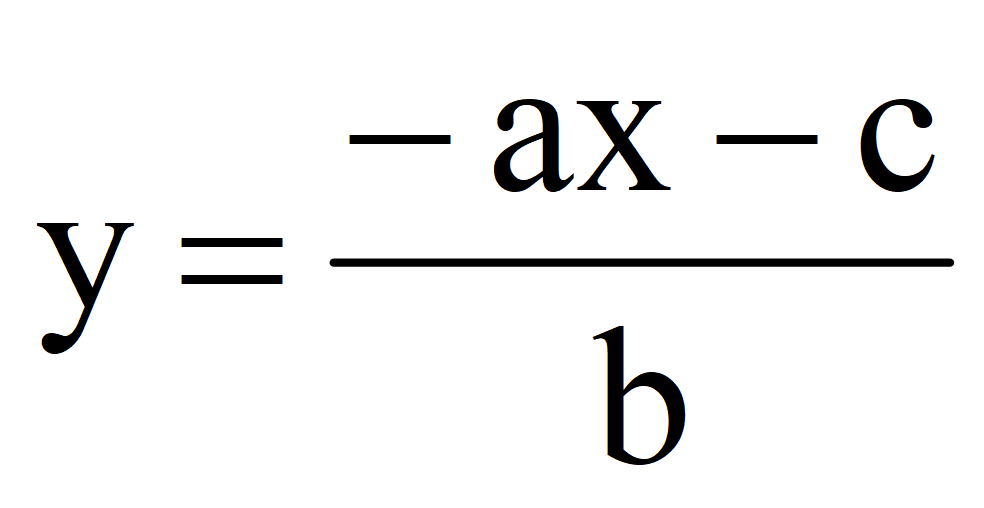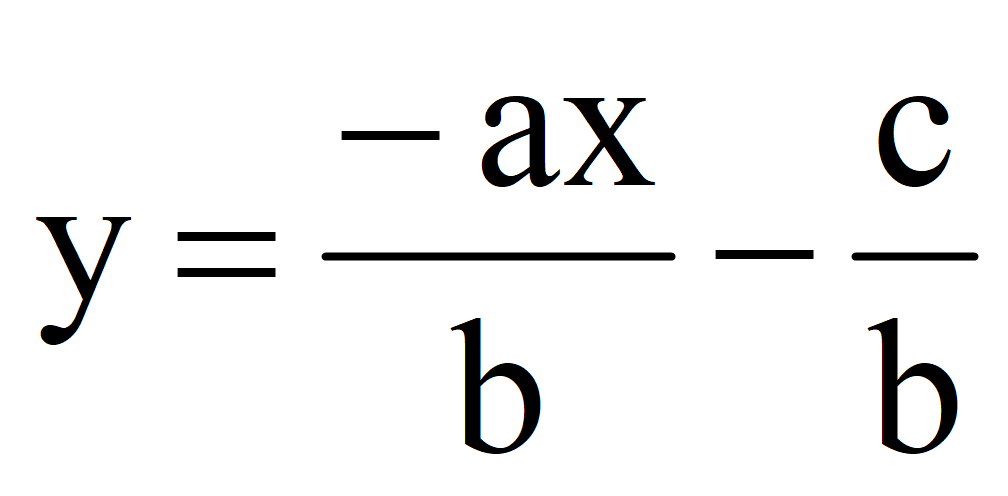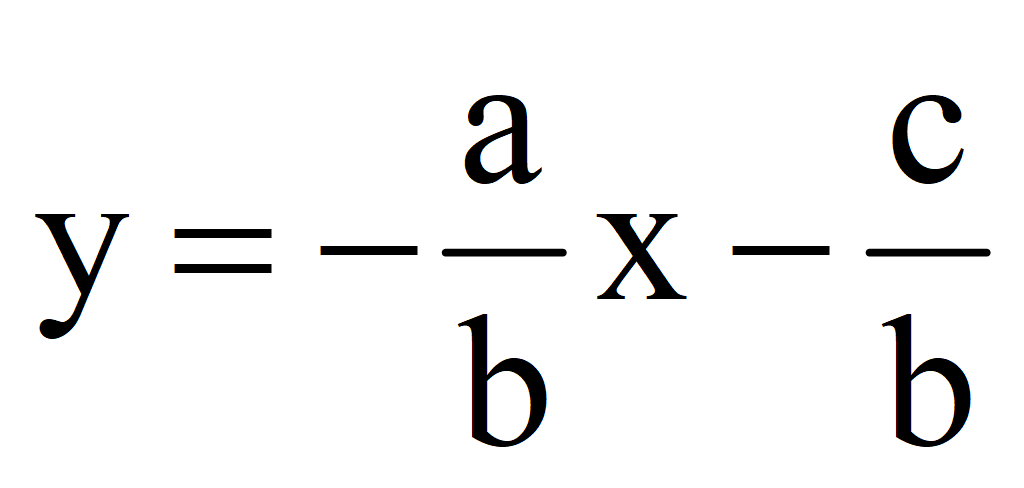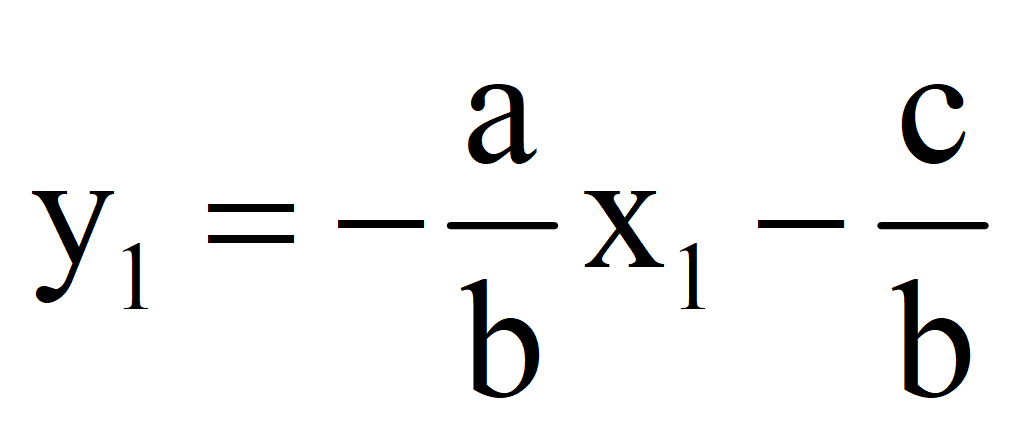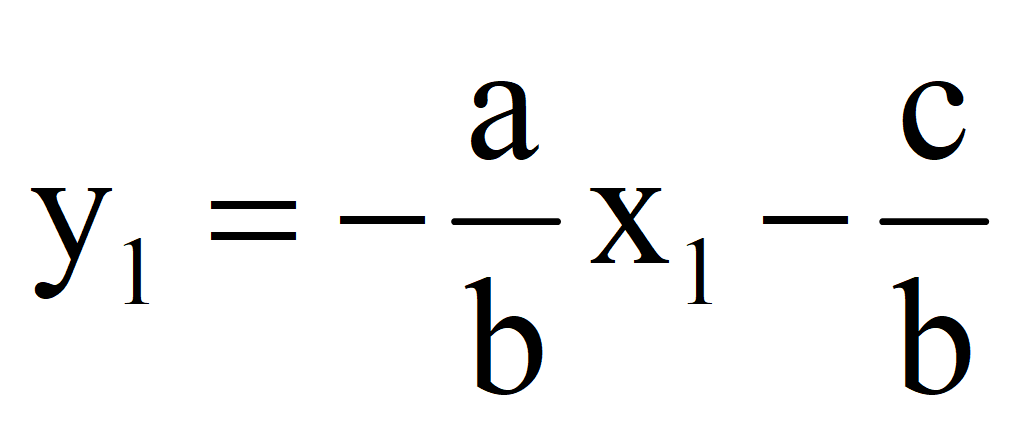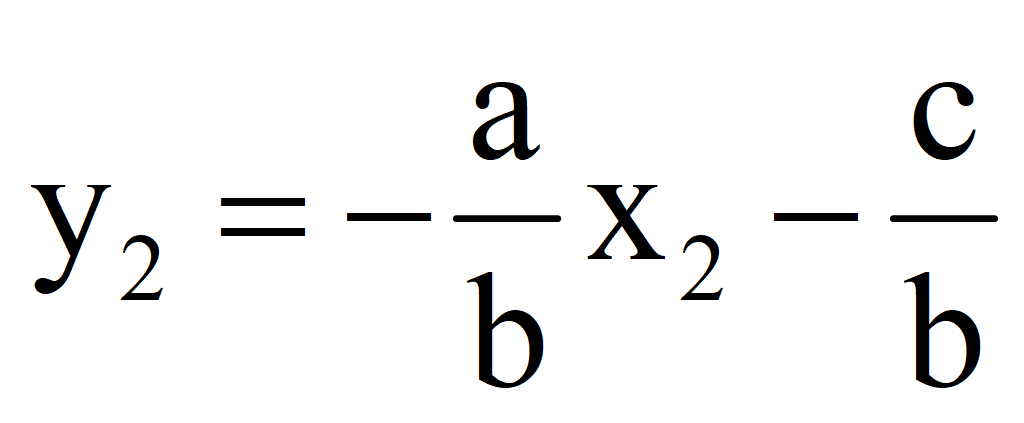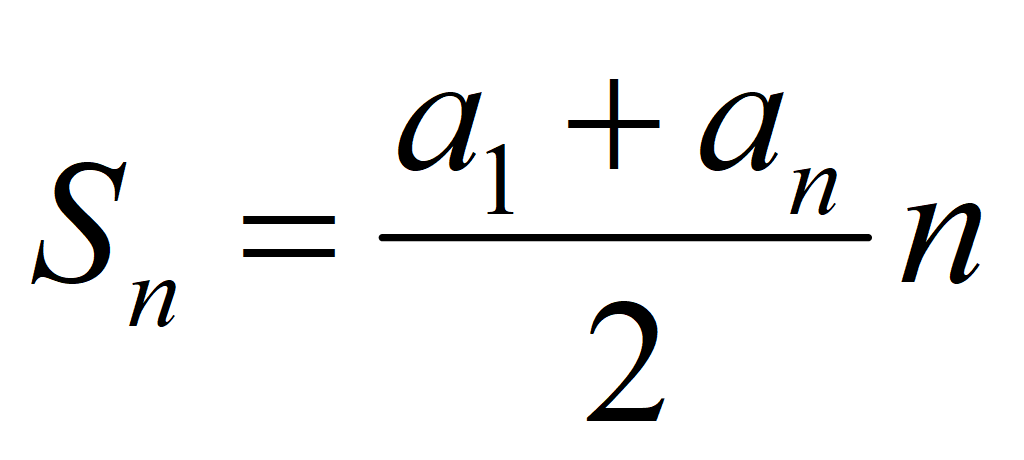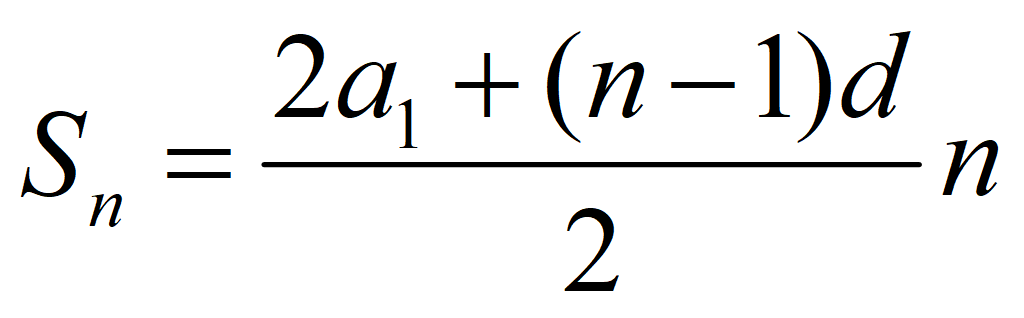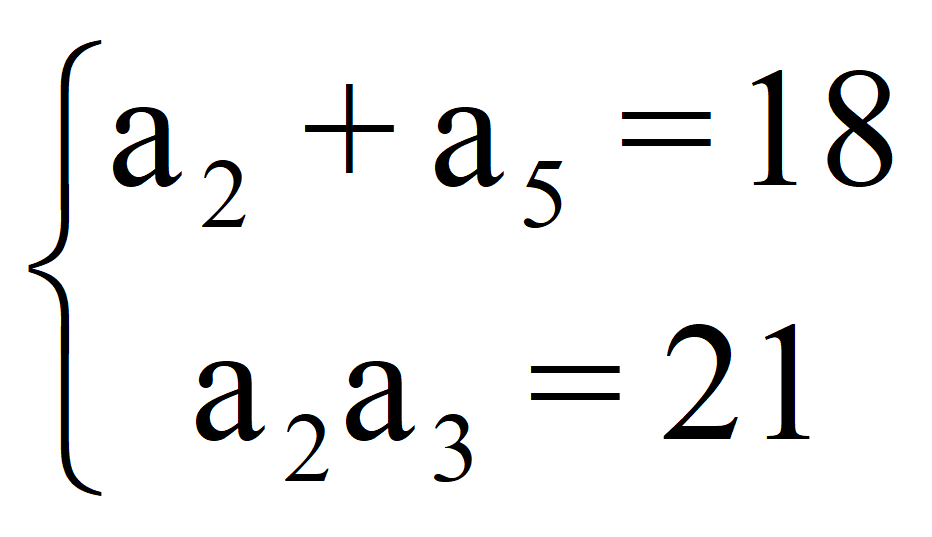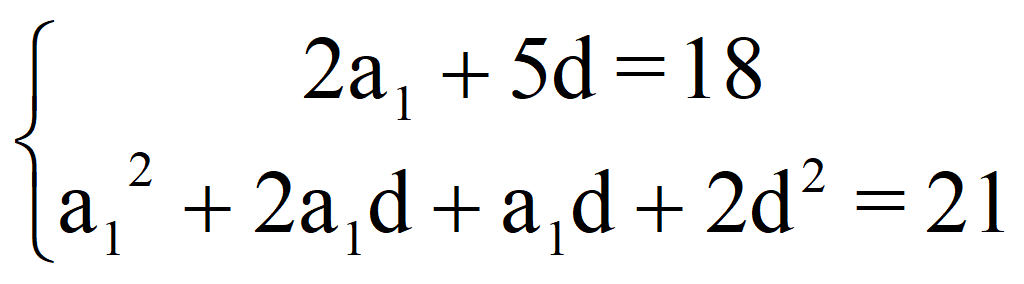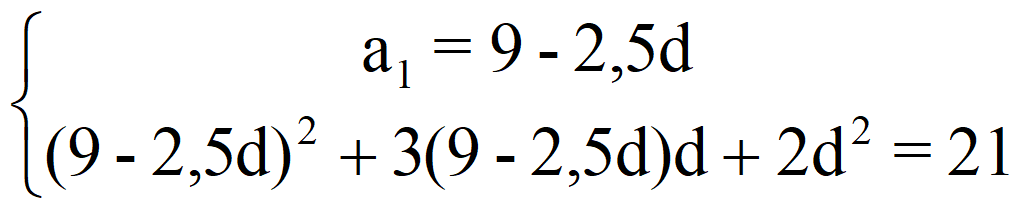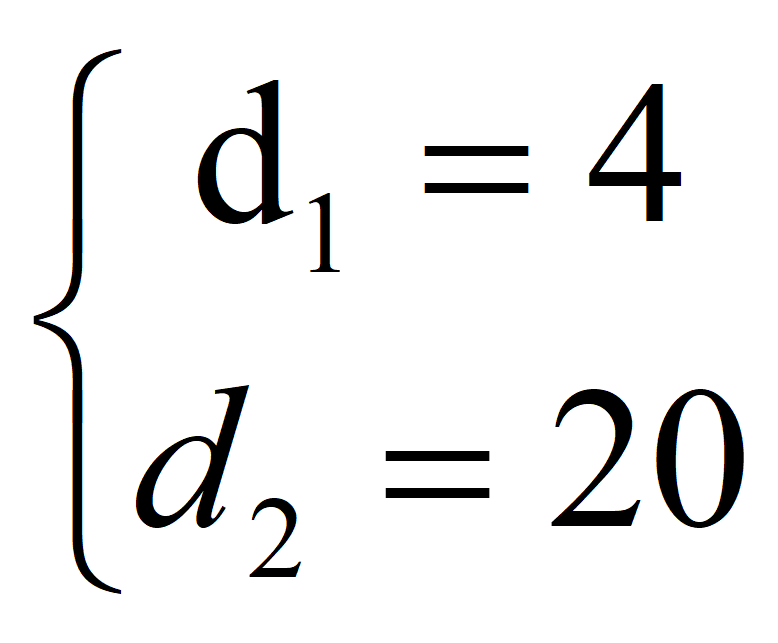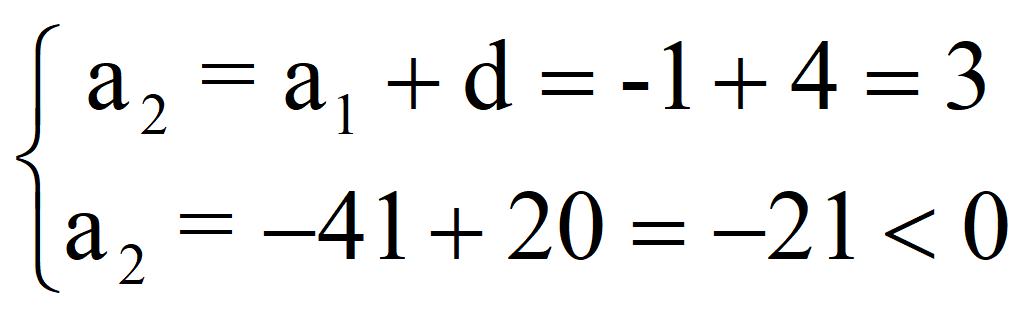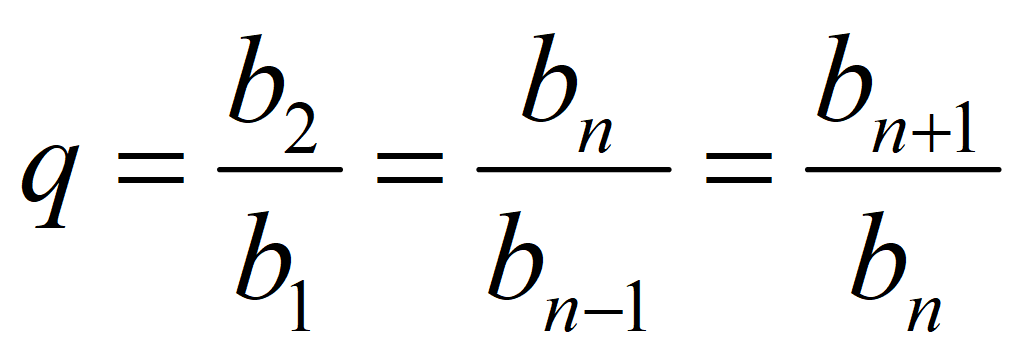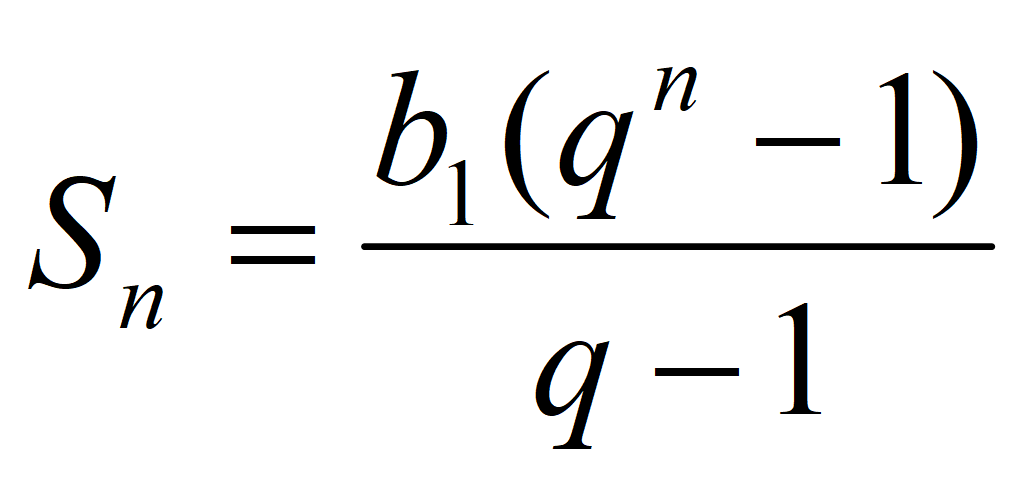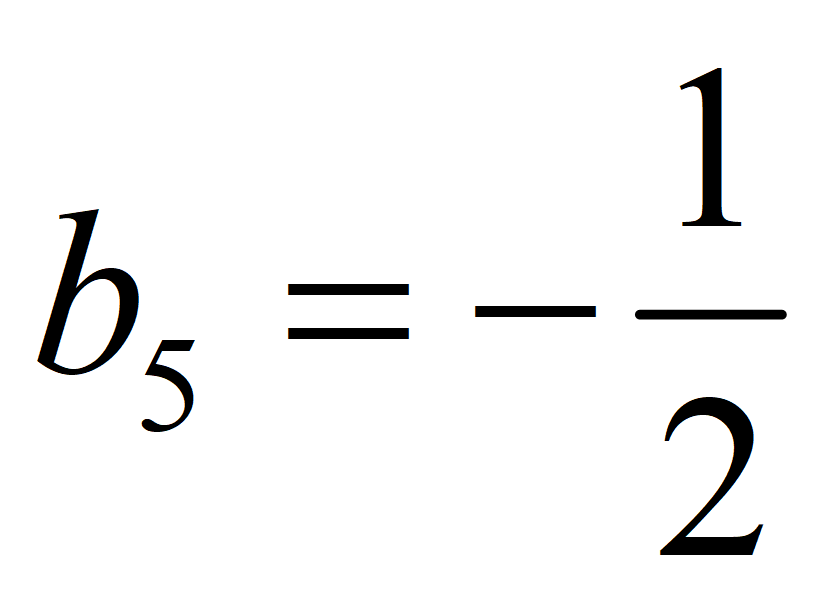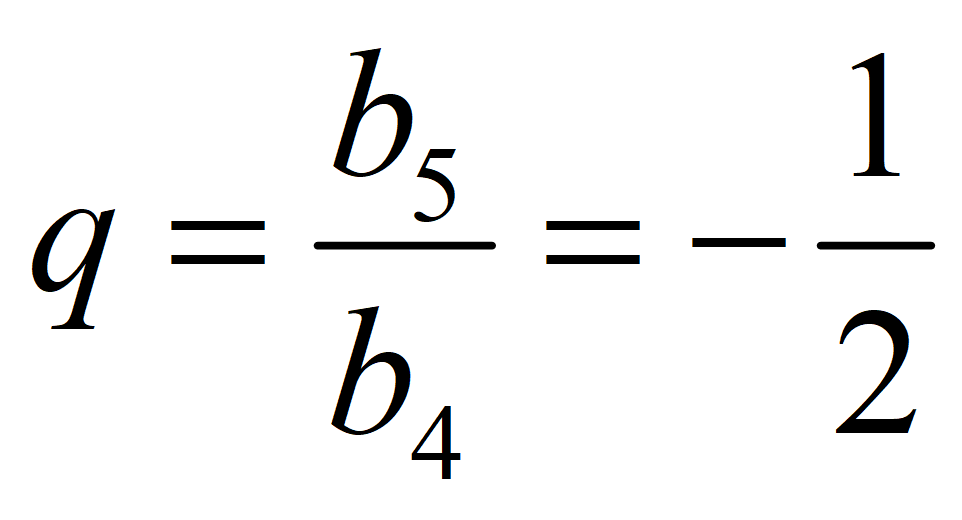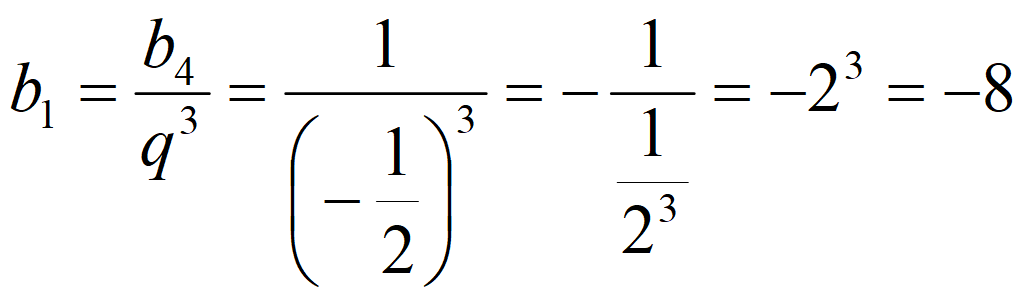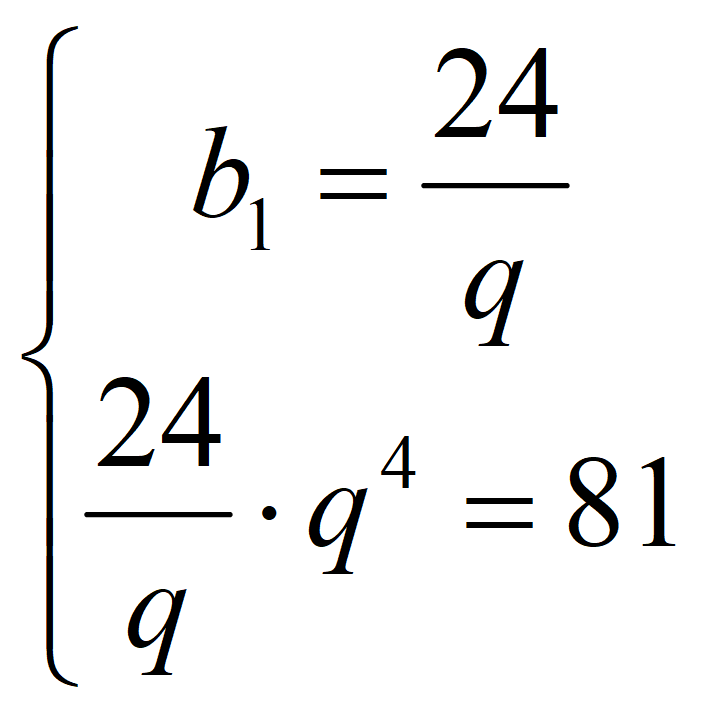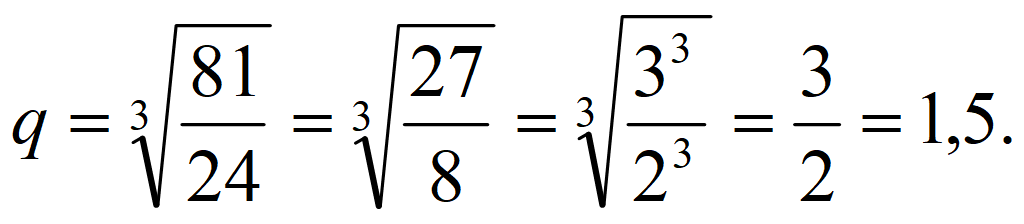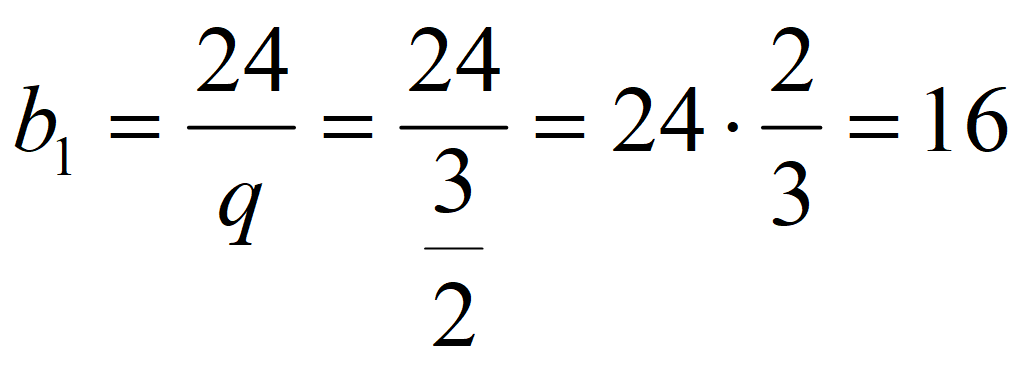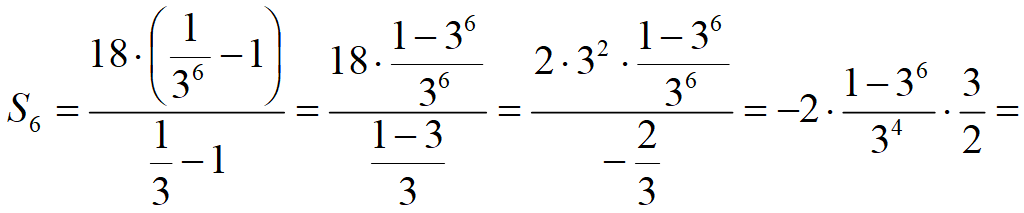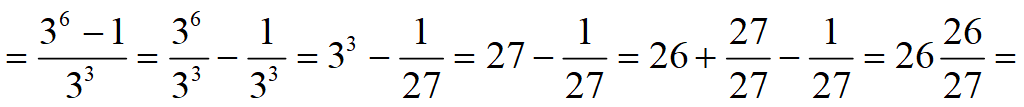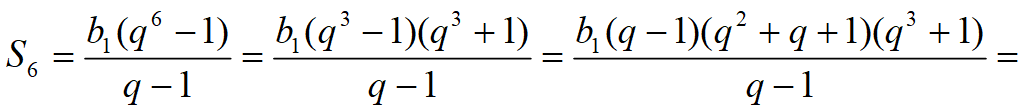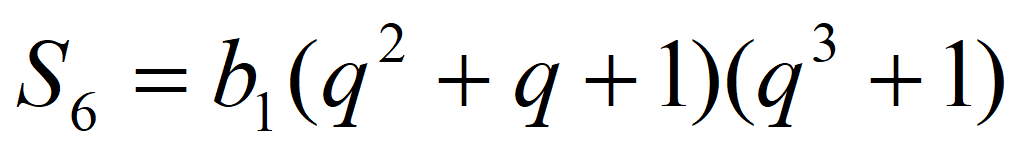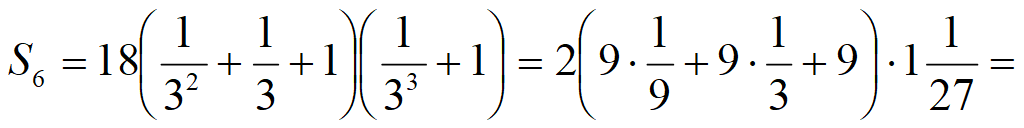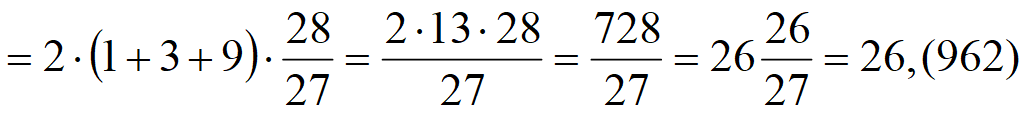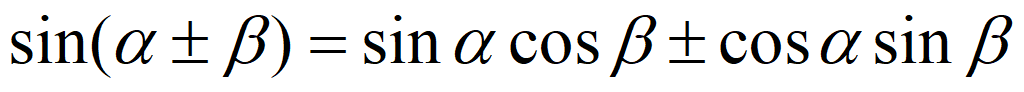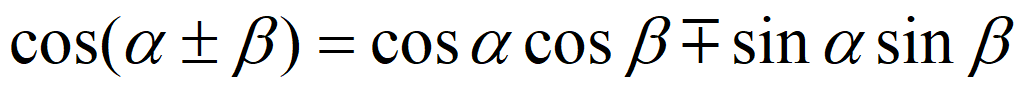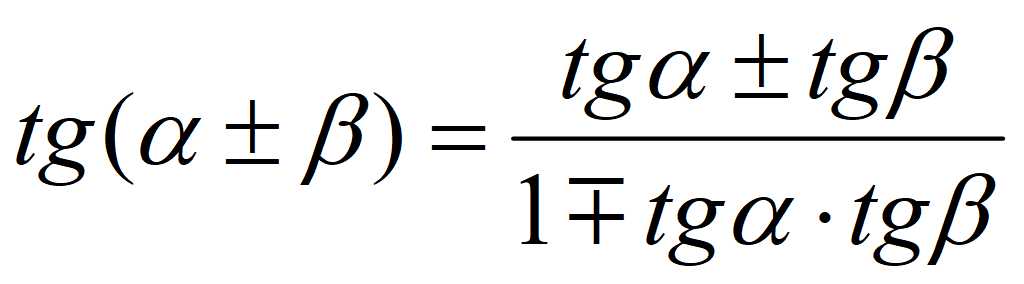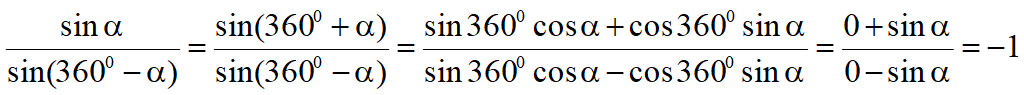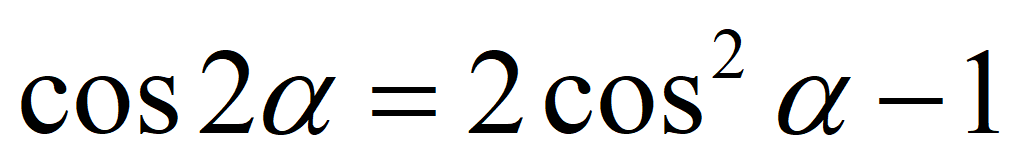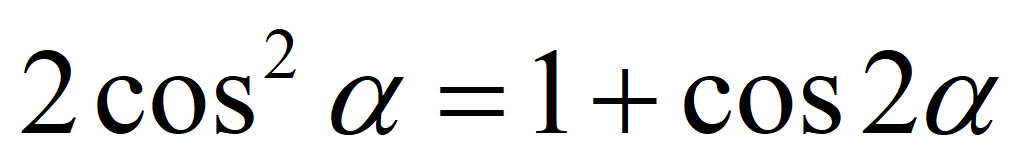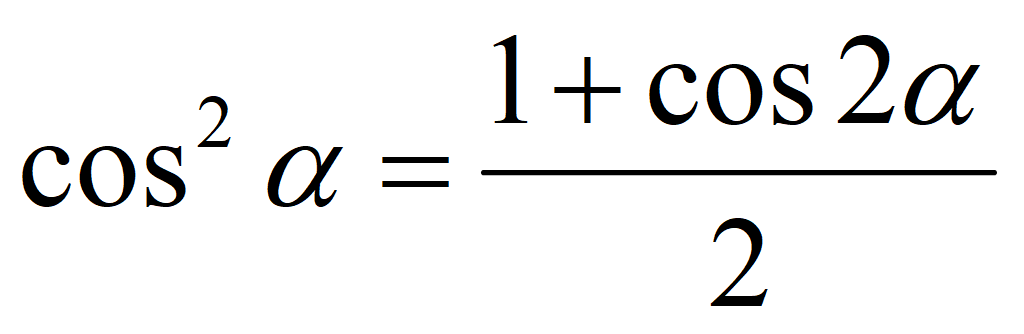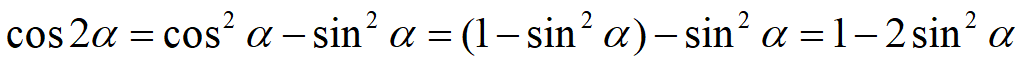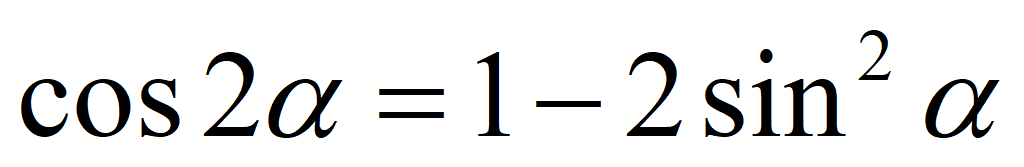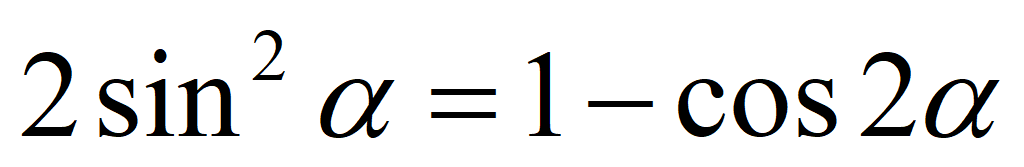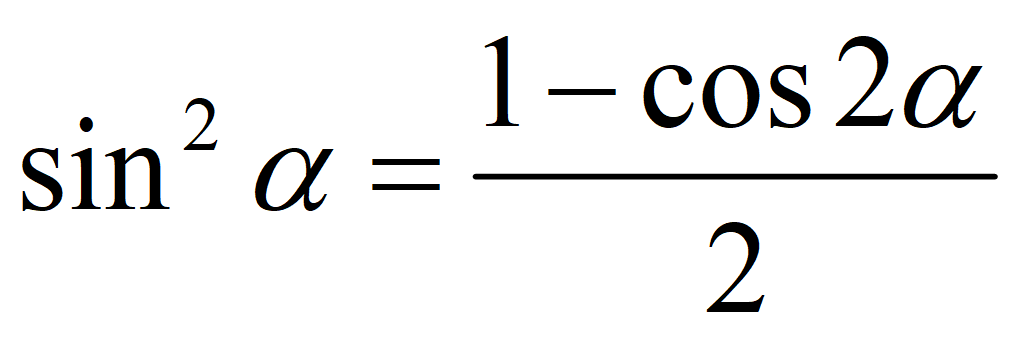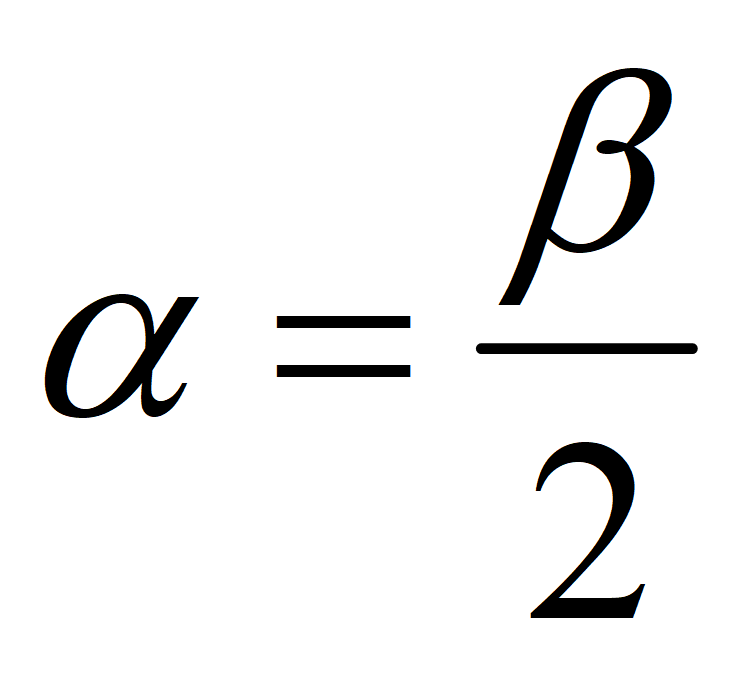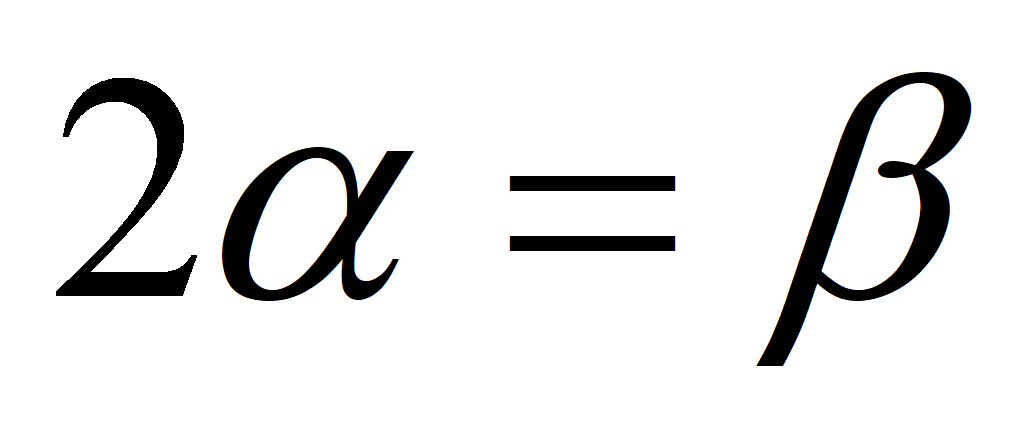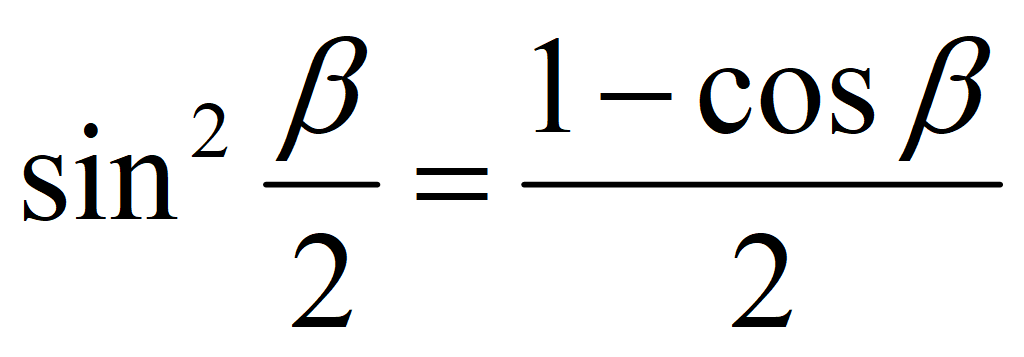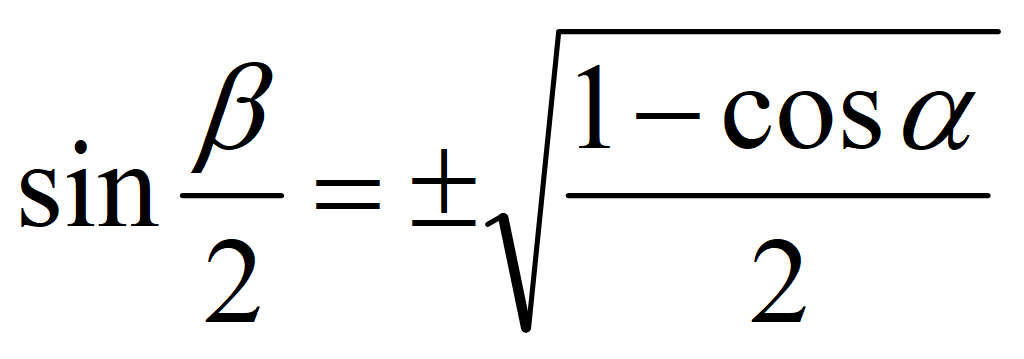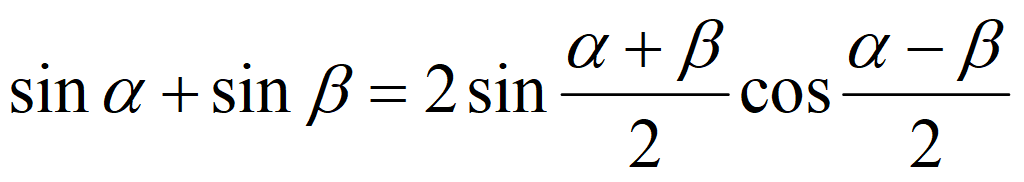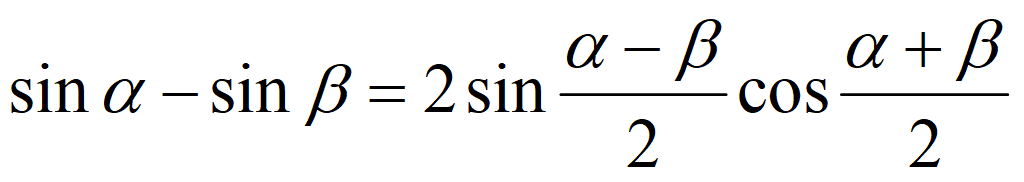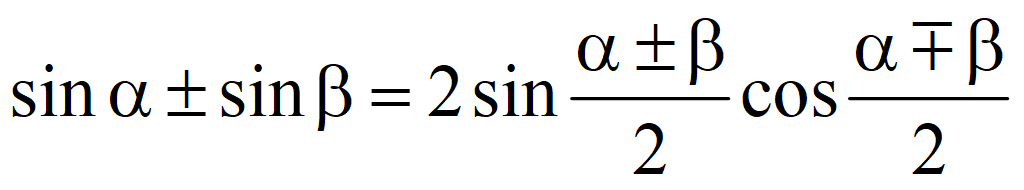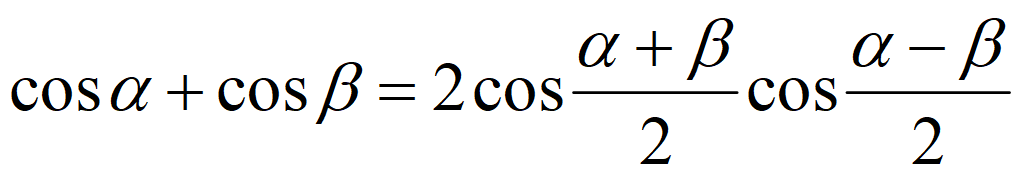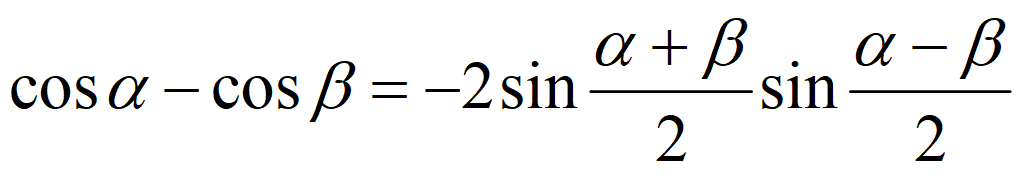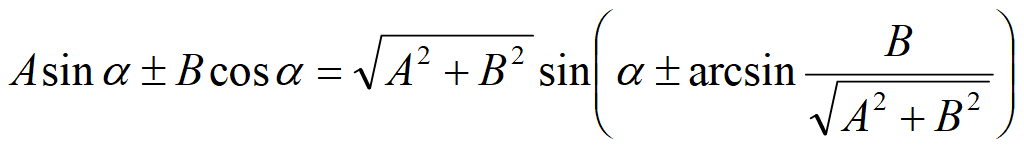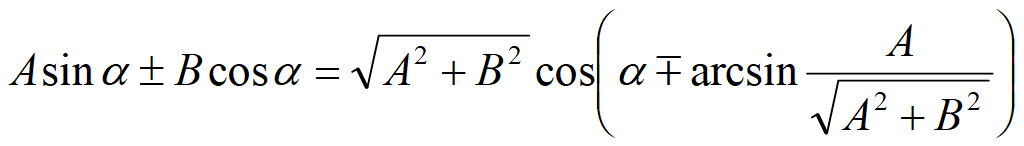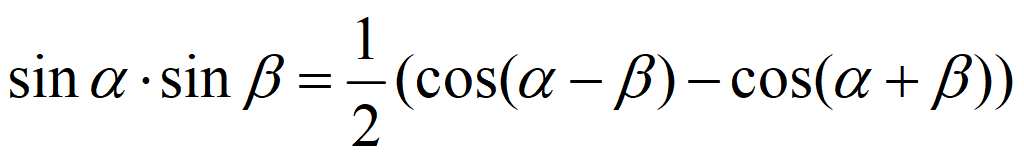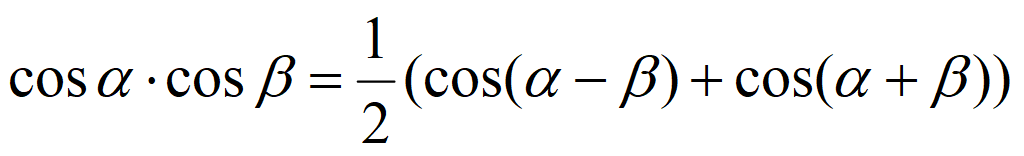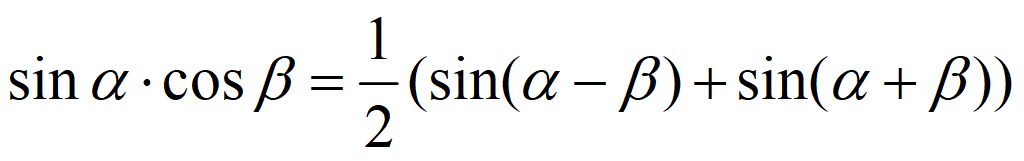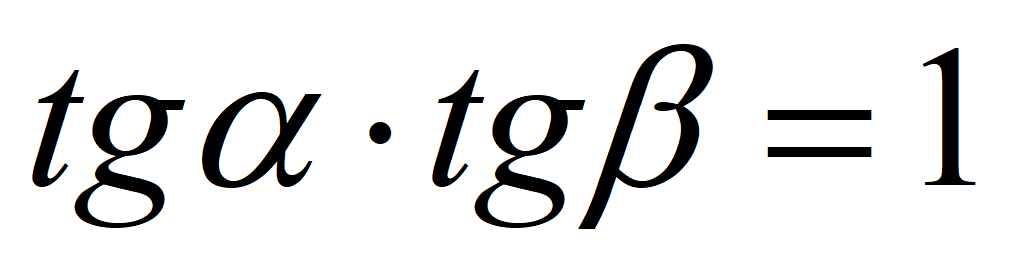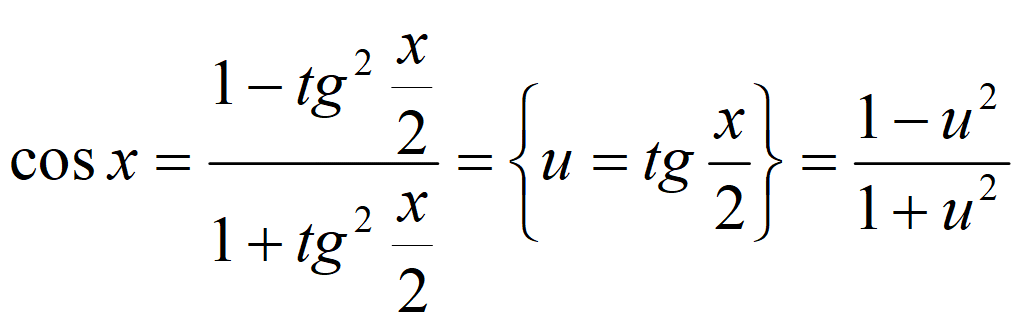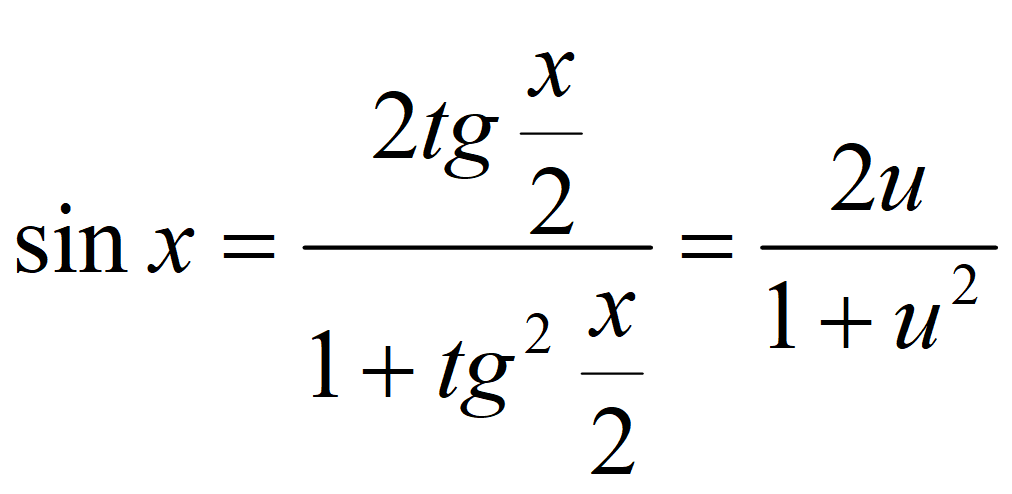Все формулы по алгебре по уравнениям

Все формулы по алгебре по уравнениям

Последние две формулы также часто удобно использовать в виде:

Квадратное уравнение и формула разложения квадратного трехчлена на множители

Пусть квадратное уравнение имеет вид:

Тогда дискриминант находят по формуле:

Если D > 0, то квадратное уравнение имеет два корня, которые находят по формуле:

Если D = 0, то квадратное уравнение имеет один корень (его кратность: 2), который ищется по формуле:

Если D 0. Ноль можно возводить только в положительную степень.

Основные свойства математических корней:

Для арифметических корней:

Последнее справедливо: если n – нечетное, то для любого a; если же n – четное, то только при a больше либо равном нолю. Для корня нечетной степени выполняется также следующее равенство:

Для корня четной степени имеется следующее свойство:

Формулы с логарифмами

Определение логарифма:

Определение логарифма можно записать и другим способом:

Свойства логарифмов:

Вынесение степени за знак логарифма:

Другие полезные свойства логарифмов:

Арифметическая прогрессия

Формулы n-го члена арифметической прогрессии:

Соотношение между тремя соседними членами арифметической прогрессии:

Формула суммы арифметической прогрессии:

Свойство арифметической прогрессии:

Геометрическая прогрессия

Формулы n-го члена геометрической прогрессии:

Соотношение между тремя соседними членами геометрической прогрессии:

Формула суммы геометрической прогрессии:

Формула суммы бесконечно убывающей геометрической прогрессии:

Свойство геометрической прогрессии:

Тригонометрия

Пусть имеется прямоугольный треугольник:

Тогда, определение синуса:

Основное тригонометрическое тождество:

Простейшие следствия из основного тригонометрического тождества:

Формулы двойного угла

Синус двойного угла:

Косинус двойного угла:

Тангенс двойного угла:

Котангенс двойного угла:

Тригонометрические формулы сложения

Тригонометрические формулы преобразования суммы в произведение

Тригонометрические формулы преобразования произведения в сумму

Произведение синуса и косинуса:

Формулы понижения степени

Формула понижения степени для синуса:

Формула понижения степени для косинуса:

Формула понижения степени для тангенса:

Формула понижения степени для котангенса:

Формулы половинного угла

Формула половинного угла для тангенса:

Формула половинного угла для котангенса:

Тригонометрические формулы приведения

Формулы приведения задаются в виде таблицы:

Тригонометрическая окружность

По тригонометрической окружности легко определять табличные значения тригонометрических функций:

Тригонометрические уравнения

Формулы решений простейших тригонометрических уравнений. Для синуса существует две равнозначные формы записи решения:

Для остальных тригонометрических функций запись однозначна. Для косинуса:

Решение тригонометрических уравнений в некоторых частных случаях:

Геометрия на плоскости (планиметрия)

Пусть имеется произвольный треугольник:

Тогда, сумма углов треугольника:

Площадь треугольника через две стороны и угол между ними:

Площадь треугольника через сторону и высоту опущенную на неё:

Полупериметр треугольника находится по следующей формуле:

Формула Герона для площади треугольника:

Площадь треугольника через радиус описанной окружности:

Основное свойство высот треугольника:

Еще одно полезное свойство высот треугольника:

Теорема косинусов:

Теорема синусов:

Радиус окружности, вписанной в правильный треугольник:

Радиус окружности, описанной около правильного треугольника:

Площадь правильного треугольника:

Теорема Пифагора для прямоугольного треугольника (c — гипотенуза, a и b — катеты):

Радиус окружности, вписанной в прямоугольный треугольник:

Радиус окружности, описанной вокруг прямоугольного треугольника:

Площадь прямоугольного треугольника (h — высота опущенная на гипотенузу):

Свойства высоты, опущенной на гипотенузу прямоугольного треугольника:

Длина средней линии трапеции:

Площадь параллелограмма через сторону и высоту опущенную на неё:

Площадь параллелограмма через две стороны и угол между ними:

Площадь квадрата через длину его стороны:

Площадь квадрата через длину его диагонали:

Площадь ромба (первая формула — через две диагонали, вторая — через длину стороны и угол между сторонами):

Площадь прямоугольника через две смежные стороны:

Площадь произвольного выпуклого четырёхугольника через две диагонали и угол между ними:

Связь площади произвольной фигуры, её полупериметра и радиуса вписанной окружности (очевидно, что формула выполняется только для фигур в которые можно вписать окружность, т.е. в том числе для любых треугольников):

Теорема о пропорциональных отрезках хорд:

Теорема о касательной и секущей:

Теорема о двух секущих:

Теорема о центральном и вписанном углах (величина центрального угла в два раза больше величины вписанного угла, если они опираются на общую дугу):

Свойство вписанных углов (все вписанные углы опирающиеся на общую дугу равны между собой):

Свойство центральных углов и хорд:

Свойство центральных углов и секущих:

Условие, при выполнении которого возможно вписать окружность в четырёхугольник:

Условие, при выполнении которого возможно описать окружность вокруг четырёхугольника:

Сумма углов n-угольника:

Центральный угол правильного n-угольника:

Площадь правильного n-угольника:

Длина окружности:

Длина дуги окружности:

Площадь круга:

Площадь кругового сегмента:

Геометрия в пространстве (стереометрия)

Главная диагональ куба:

Объём прямоугольного параллелепипеда:

Главная диагональ прямоугольного параллелепипеда (эту формулу также можно назвать: «трёхмерная Теорема Пифагора»):

Площадь боковой поверхности прямой призмы (P – периметр основания, l – боковое ребро, в данном случае равное высоте h):

Объём кругового цилиндра:

Площадь боковой поверхности прямого кругового цилиндра:

Площадь боковой поверхности правильной пирамиды (P – периметр основания, l – апофема, т.е. высота боковой грани):

Объем кругового конуса:

Площадь боковой поверхности прямого кругового конуса:

Длина образующей прямого кругового конуса:

Объём шара:

Площадь поверхности шара (или, другими словами, площадь сферы):

Координаты

Длина отрезка на координатной оси:

Длина отрезка на координатной плоскости:

Длина отрезка в трёхмерной системе координат:

Координаты середины отрезка (для координатной оси используется только первая формула, для координатной плоскости — первые две формулы, для трехмерной системы координат — все три формулы):

Таблица умножения

Таблица квадратов двухзначных чисел

Расширенная PDF версия документа «Все главные формулы по школьной математике»:

Как успешно подготовиться к ЦТ по физике и математике?

Для того чтобы успешно подготовиться к ЦТ по физике и математике, среди прочего, необходимо выполнить три важнейших условия:

1. Изучить все темы и выполнить все тесты и задания приведенные в учебных материалах на этом сайте. Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день. Дело в том, что ЦТ это экзамен, где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач.
2. Выучить все формулы и законы в физике, и формулы и методы в математике. На самом деле, выполнить это тоже очень просто, необходимых формул по физике всего около 200 штук, а по математике даже чуть меньше. В каждом из этих предметов есть около десятка стандартных методов решения задач базового уровня сложности, которые тоже вполне можно выучить, и таким образом, совершенно на автомате и без затруднений решить в нужный момент большую часть ЦТ. После этого Вам останется подумать только над самыми сложными задачами.
3. Посетить все три этапа репетиционного тестирования по физике и математике. Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.

Успешное, старательное и ответственное выполнение этих трех пунктов, а также ответственная проработка итоговых тренировочных тестов, позволит Вам показать на ЦТ отличный результат, максимальный из того, на что Вы способны.

Нашли ошибку?

Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на электронную почту (адрес электронной почты здесь). В письме укажите предмет (физика или математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка. Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.

ЗАПРЕЩЕНО использование представленных на сайте материалов или их частей в любых коммерческих целях, а также их копирование, перепечатка, повторная публикация или воспроизведение в любой форме. Нарушение прав правообладателей преследуется по закону. Подробнее.

Математика: Все главные формулы

Оглавление:

Формулы сокращенного умножения

Последние две формулы также часто удобно использовать в виде:

Квадратное уравнение и формула разложения квадратного трехчлена на множители

Пусть квадратное уравнение имеет вид:

Тогда дискриминант находят по формуле:

Если D > 0, то квадратное уравнение имеет два корня, которые находят по формуле:

Если D = 0, то квадратное уравнение имеет один корень (его кратность: 2), который ищется по формуле:

Если D 0. Ноль можно возводить только в положительную степень.

Основные свойства математических корней:

Для арифметических корней:

Последнее справедливо: если n – нечетное, то для любого a; если же n – четное, то только при a больше либо равном нолю. Для корня нечетной степени выполняется также следующее равенство:

Для корня четной степени имеется следующее свойство:

Формулы с логарифмами

Определение логарифма:

Определение логарифма можно записать и другим способом:

Свойства логарифмов:

Вынесение степени за знак логарифма:

Другие полезные свойства логарифмов:

Арифметическая прогрессия

Формулы n-го члена арифметической прогрессии:

Соотношение между тремя соседними членами арифметической прогрессии:

Формула суммы арифметической прогрессии:

Свойство арифметической прогрессии:

Геометрическая прогрессия

Формулы n-го члена геометрической прогрессии:

Соотношение между тремя соседними членами геометрической прогрессии:

Формула суммы геометрической прогрессии:

Формула суммы бесконечно убывающей геометрической прогрессии:

Свойство геометрической прогрессии:

Тригонометрия

Пусть имеется прямоугольный треугольник:

Тогда, определение синуса:

Основное тригонометрическое тождество:

Простейшие следствия из основного тригонометрического тождества:

Формулы двойного угла

Синус двойного угла:

Косинус двойного угла:

Тангенс двойного угла:

Котангенс двойного угла:

Тригонометрические формулы сложения

Тригонометрические формулы преобразования суммы в произведение

Тригонометрические формулы преобразования произведения в сумму

Произведение синуса и косинуса:

Формулы понижения степени

Формула понижения степени для синуса:

Формула понижения степени для косинуса:

Формула понижения степени для тангенса:

Формула понижения степени для котангенса:

Формулы половинного угла

Формула половинного угла для тангенса:

Формула половинного угла для котангенса:

Тригонометрические формулы приведения

Формулы приведения задаются в виде таблицы:

Тригонометрическая окружность

По тригонометрической окружности легко определять табличные значения тригонометрических функций:

Тригонометрические уравнения

Формулы решений простейших тригонометрических уравнений. Для синуса существует две равнозначные формы записи решения:

Для остальных тригонометрических функций запись однозначна. Для косинуса:

Решение тригонометрических уравнений в некоторых частных случаях:

Геометрия на плоскости (планиметрия)

Пусть имеется произвольный треугольник:

Тогда, сумма углов треугольника:

Площадь треугольника через две стороны и угол между ними:

Площадь треугольника через сторону и высоту опущенную на неё:

Полупериметр треугольника находится по следующей формуле:

Формула Герона для площади треугольника:

Площадь треугольника через радиус описанной окружности:

Основное свойство высот треугольника:

Еще одно полезное свойство высот треугольника:

Теорема косинусов:

Теорема синусов:

Радиус окружности, вписанной в правильный треугольник:

Радиус окружности, описанной около правильного треугольника:

Площадь правильного треугольника:

Теорема Пифагора для прямоугольного треугольника (c — гипотенуза, a и b — катеты):

Радиус окружности, вписанной в прямоугольный треугольник:

Радиус окружности, описанной вокруг прямоугольного треугольника:

Площадь прямоугольного треугольника (h — высота опущенная на гипотенузу):

Свойства высоты, опущенной на гипотенузу прямоугольного треугольника:

Длина средней линии трапеции:

Площадь параллелограмма через сторону и высоту опущенную на неё:

Площадь параллелограмма через две стороны и угол между ними:

Площадь квадрата через длину его стороны:

Площадь квадрата через длину его диагонали:

Площадь ромба (первая формула — через две диагонали, вторая — через длину стороны и угол между сторонами):

Площадь прямоугольника через две смежные стороны:

Площадь произвольного выпуклого четырёхугольника через две диагонали и угол между ними:

Связь площади произвольной фигуры, её полупериметра и радиуса вписанной окружности (очевидно, что формула выполняется только для фигур в которые можно вписать окружность, т.е. в том числе для любых треугольников):

Теорема о пропорциональных отрезках хорд:

Теорема о касательной и секущей:

Теорема о двух секущих:

Теорема о центральном и вписанном углах (величина центрального угла в два раза больше величины вписанного угла, если они опираются на общую дугу):

Свойство вписанных углов (все вписанные углы опирающиеся на общую дугу равны между собой):

Свойство центральных углов и хорд:

Свойство центральных углов и секущих:

Условие, при выполнении которого возможно вписать окружность в четырёхугольник:

Условие, при выполнении которого возможно описать окружность вокруг четырёхугольника:

Сумма углов n-угольника:

Центральный угол правильного n-угольника:

Площадь правильного n-угольника:

Длина окружности:

Длина дуги окружности:

Площадь круга:

Площадь кругового сегмента:

Геометрия в пространстве (стереометрия)

Главная диагональ куба:

Объём прямоугольного параллелепипеда:

Главная диагональ прямоугольного параллелепипеда (эту формулу также можно назвать: «трёхмерная Теорема Пифагора»):

Площадь боковой поверхности прямой призмы (P – периметр основания, l – боковое ребро, в данном случае равное высоте h):

Объём кругового цилиндра:

Площадь боковой поверхности прямого кругового цилиндра:

Площадь боковой поверхности правильной пирамиды (P – периметр основания, l – апофема, т.е. высота боковой грани):

Объем кругового конуса:

Площадь боковой поверхности прямого кругового конуса:

Длина образующей прямого кругового конуса:

Объём шара:

Площадь поверхности шара (или, другими словами, площадь сферы):

Координаты

Длина отрезка на координатной оси:

Длина отрезка на координатной плоскости:

Длина отрезка в трёхмерной системе координат:

Координаты середины отрезка (для координатной оси используется только первая формула, для координатной плоскости — первые две формулы, для трехмерной системы координат — все три формулы):

7 класс

Прямоугольная система координат — это пересекающиеся взаимно перпендикулярные координатные прямые с началом отсчета в точке их пересечения, превращающая плоскость в координатную плоскость.

Линейное уравнение с двумя переменными

где a , b , c — коэффициенты (числа);

x , y — переменные.

Решением уравнения с двумя переменными, например ax + by + c = 0, называют пару чисел ( x ; y ), удовлетворяющих этому уравнению, то есть дающих верное числовое равенство при подстановке решения в заданное уравнение.

Задача. Найти два решения уравнения 2 x + 5 y + 7 = 0 и построить график функции

Выразим y через x

Первое решение (0; -1,4).

Второе решение (-3; -0,2).

Алгоритм нахождения решения линейного уравнения с двумя переменными ax + by + c =0

1.Выразить переменную y через переменную x

2.Задать конкретное значение переменной x = x ₁; найти значение y = y ₁

Алгоритм построения графика линейного уравнения с двумя переменными ax + by + c =0

1.Выразить переменную y через переменную x

2.Задать конкретное значение переменной x = x ₁; найти значение y = y ₁

3.Задать другое конкретное значение переменной x = x ₂; найти значение y = y ₂

4.Построить точки ( x ₁; y ₁) и ( x ₂; y ₂) на координатной плоскости xOy .

5.Через эти две точки провести прямую, которая и является графиком линейного уравнения ax + by + c = 0.

Задача. Построить график функции 20 x + 10 y — 5 = 0.

Выразить переменную y через переменную x

Задача. Построить график функции -40 x — 8 y + 32 = 0.

Задача. Построить график функции ax + by + c = 0 при a = 1, b = 1 и c = 1

Выразим y через x

Это уравнение линейной функции, поэтому для построения графика функции достаточно двух точек

y = — (-1) — 1 = 1 — 1 = 0.

Формулы сокращенного умножения

Квадрат суммы ( a + b ) 2 = a 2 + 2 ab + b 2 .

Квадрат разности ( a — b ) 2 = a 2 — 2 ab + b 2 .

Разность квадратов a 2 — b 2 = ( a — b )( a + b ).

Разность кубов a 3 — b 3 = (a — b)(a 2 + ab + b 2 ).

Сумма кубов a 3 + b 3 = (a + b)(a 2 – ab + b 2 ).

Куб разности (a — b) 3 = a 3 — 3a 2 b + 3ab 2 — b 3 .

Куб суммы (a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3 .

8 класс

9 класс

Числовая функция

Функция y = f ( x ) – это правило f , которое устанавливает зависимость между конкретным значением независимой переменной x (аргументом) и зависимой от нее переменной y , имеющей единственное значение.

Область определения функции

Область определения функции D ( f ) или X – это множество значений независимой переменной x , при которых функция y = f ( x ) существует.

Задание функции y = f ( x ) на области определения X или D ( f )

Задать функцию y = f ( x ) на области определения X или D ( f ) – значит каждому аргументу x из множества X или D ( f ) поставить в соответствие единственное значение y . Задание функции записывается одним из способов:

Область значений функции

Область значений функции E ( f ) – это множество всех значений функции y = f ( x ) при x ϵ X .

Способы задания функции

Основные способы задания фунций:

1.Аналитический – функция y = f ( x ) задается формулой (формулами).

2.Графический — графиком функции y = f ( x ).

3.Табличный — таблицей со переменной x и соответствующими им значениями y .

Четные и нечетные функции

Для четной функции f ( x ), x ϵ X выполняется равенство

для нечетной функции f ( x ), x ϵ X выполняется равенство

для любого x из множества X .

Область определения D ( f ) четной или нечетной функции y = f ( x ) является симметричным множеством.

Если область определения D ( f ) не является симметричным множеством или условия четности и нечетности функции f ( x ) не выполняются, то функция ни четная, ни нечетная.

Законы сложения

1.Переместительный закон a + b = b + a .

2.Распределительный закон ( a + b ) + c = a + ( b + c ).

Для любых рациональных чисел a , b и c справедливы законы умножения

1.Переместительный закон ab = ba .

2.Сочетательный закон ( ab ) c = a ( bc ).

3.Распределительный закон ( a + b ) c = ac + bc .

Числовая последовательность

Числовой последовательностью называют функцию y = f ( x ) натурального аргумента x ϵ N , которую обозначают y = f ( n ) или y ₁, y ₂, …, y _n , где индекс n ϵ N .

График числовой последовательности представляет из себя набор точек с натуральным аргументом и значениями функции, вычисленными в этих точках.

Аналитический способ задания числовой последовательности

Последовательность задается аналитически формулой n -го члена y _n = f ( n ).

Словесный способ задания последовательности

При словесном способе правило составления последовательности описывается словами, а не формулой.

Рекуррентный способ задания последовательности

При рекуррентном (от латинского слова recurrere – возвращаться) способе n -ный член последовательности вычисляется по правилу или формуле на основе предыдущих членов последовательности. Обычно задаются 1-2 первых члена последовательности.

Например, последовательность y ₁ = 2; y _n = y _{n -1} + 3, при n > 1 задана рекуррентно.

Арифметическая прогрессия

Арифметической прогрессией называется числовая последовательность, каждый последующий член, которой, начиная со второго, отличается от предыдущего на величину разности арифметической последовательности d .

Арифметическая прогрессия задается рекуррентно:

где первый член a ₁ и разность арифметической прогрессии d – заданны числами;

a _n – член прогрессии, начиная со второго;

a _{n -1} – предыдущий член арифметической прогрессии.

d — разность между последующим и предыдущим членами прогрессии:

n – ный член арифметической прогрессии

Сумма n членов арифметической прогрессии:

Подставим a _n = a ₁ + (n – 1)d

Задача 16.31 [Алгебра. 9 класс. В 2 ч. Ч.2. Задачник Мордкович А.Г. и др. 2010 — 223с].

Подставляем в заданную систему

и получаем систему уравнений

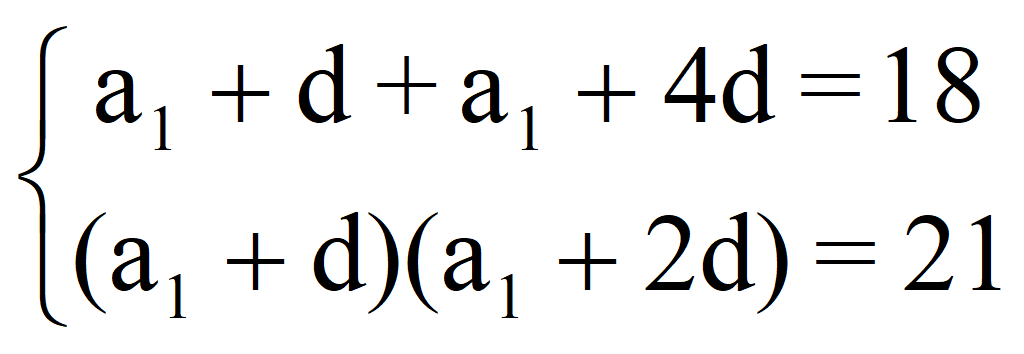
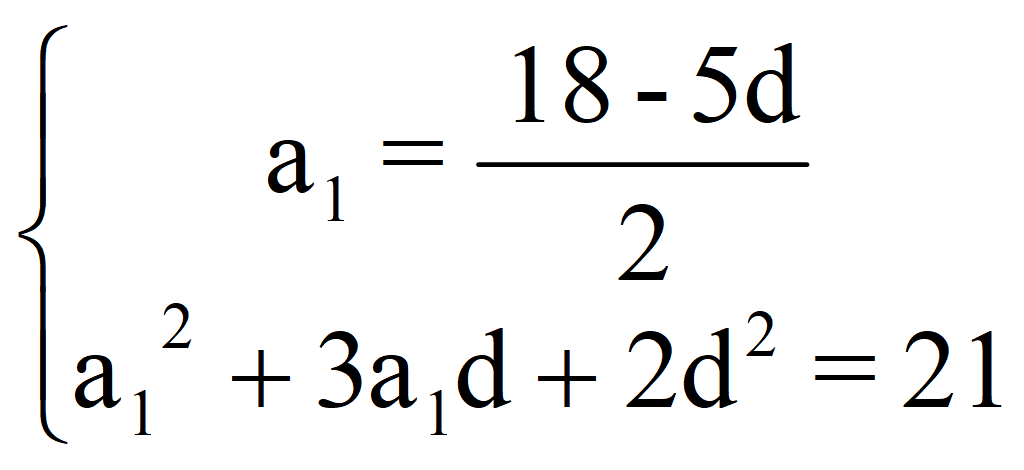
81 – 45 d + 6,25 d 2 + 27 d – 7,5 d 2 + 2 d 2 = 21;

0,75 d 2 – 18 d + 81 – 21 = 0;

0,75 d 2 – 18 d + 60 = 0.

Разделим на 0,75, то есть умножим на 4/3

d 2 – 24 d + 80 = 0.

По теореме Виета

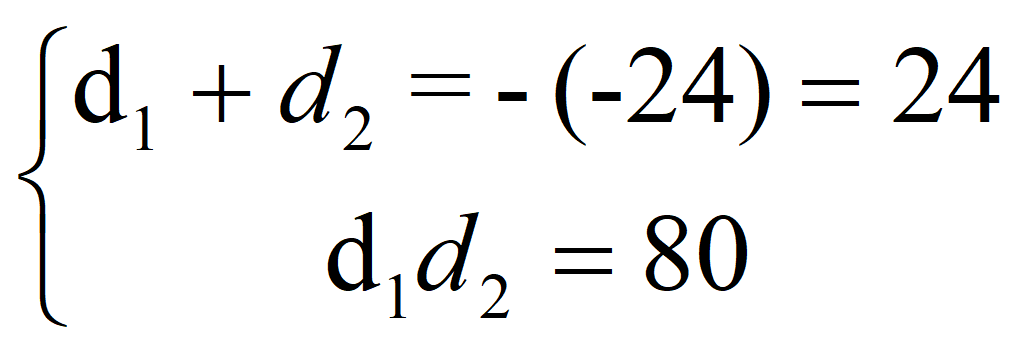
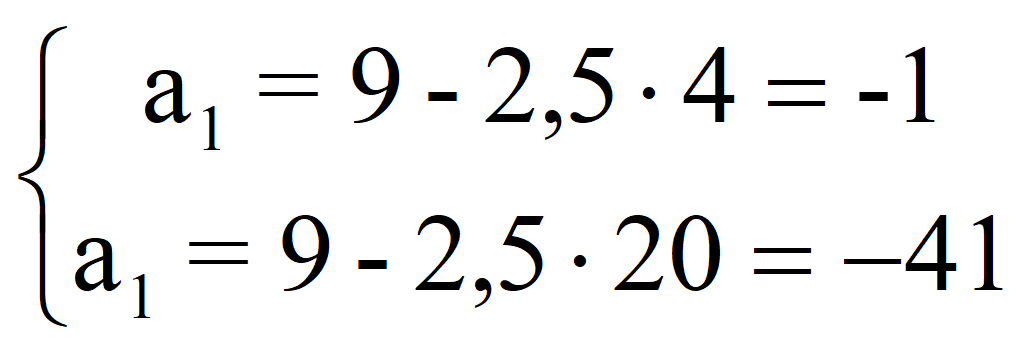
Следовательно , a ₁ = -1; d = 4; a ₂ = 3;

Геометрическая прогрессия

Геометрической прогрессией называется ненулевая числовая последовательность, каждый последующий член, которой, начиная со второго, получается из предыдущего умножением на знаменатель геометрической прогрессии q .

Геометрическая прогрессия задается рекуррентно:

где первый член b ₁ и знаменатель геометрической прогрессии q – заданны числами;

b _n – член прогрессии, начиная со второго;

b _{n -1} – предыдущий член арифметической прогрессии.

Знаменатель геометрической прогрессии

n -ный член геометрической прогрессии

Сумма n -членов геометрической прогрессии

Задача 17.12 (б) [Мордкович. Задачник 9 класс]

Найдите b ₁ и q для геометрической прогрессии ( b _n ), заданной следующими условиями:

b ₄ = 1,

Знаменатель геометрической прогрессии

Формула 4-го члена геометрической прогрессии:

Задача 17.22 (б) [Мордкович. Задачник 9 класс]

Найдите b ₁ и q для геометрической прогрессии ( b _n ), заданной следующими условиями:

Знаменатель геометрической прогрессии

Формула 2-го члена геометрической прогрессии:

Формула 5-го члена геометрической прогрессии:

Получаем систему уравнений

;

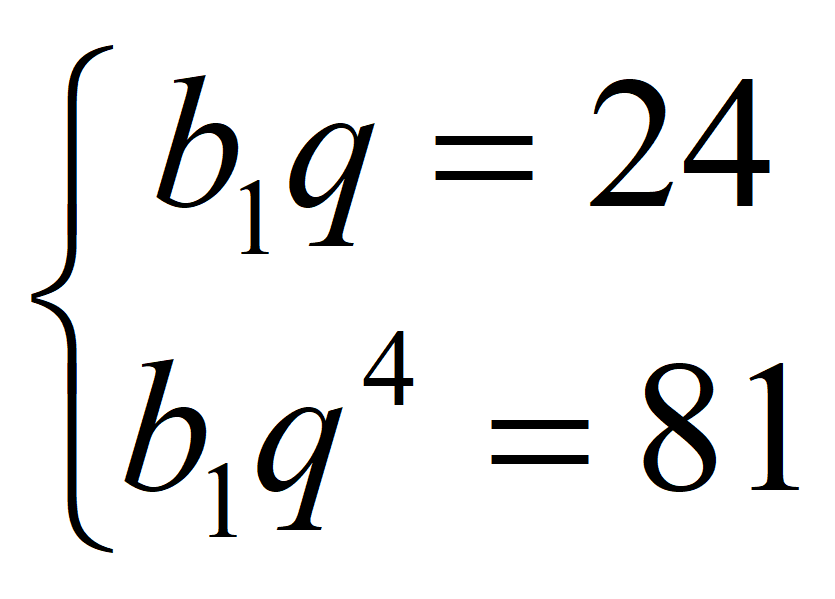
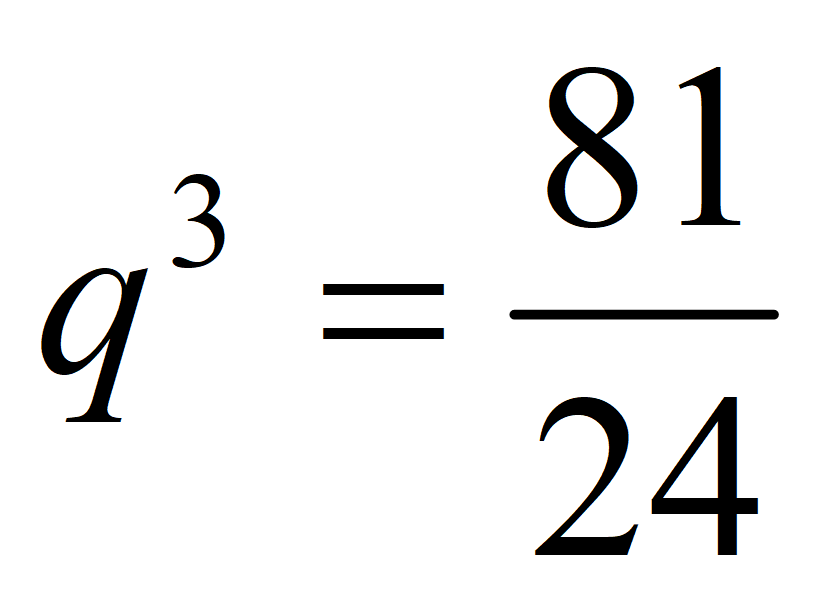
10 класс

Признак делимости на 11

Признак делимости на 7 или 13

Натуральное число делится на 7 или 13, если алгебраическая сумма чисел

Простые и составные числа

Простым называется число, имеющее только два делителя — само число и 1.

Составным называется число, имеющее больше двух делителей.

Число 1 не является ни простым, ни составным, так как делится лишь на 1.

Произвольное натуральное число, большее 1 имеет как минимум один простой делитель.

Множество простых чисел бесконечно [10].

Расстояние между двумя соседними простыми числами может быть больше любого наперед заданного натурального числа [10].

График функции y = f ( x + a )+ b , полученный из графика функции y = f ( x )

График функции y = f ( x + a ) + b , получается из графика функции y = f ( x ) путем перемещения на вектор (- a ; b ).

Обратные тригонометрические функции

Нечетными являются функции y = arcsinx и y = arctgx . Функции y = arcosx и y = arcctgx не являются ни четными, ни нечетными.

Тригонометрические формулы

Сложение и вычитание аргументов

Формулы двойного угла

sin 2 α = 2 sinαcosα

cos 2 α = cos 2 α – sin 2 α = 1 — 2 sin 2 α = 2 cos 2 α – 1

Формулы понижения степени

Сложение и вычитание функций

Преобразование произведения в сумму и разность

Если α + β = 90 0 , то

Методы решения тригонометрических уравнений

Приравнять к нулю и разбить на множители

Подстановка

Универсальная тригонометрическая подстановка

11 класс

Многочлены от одной переменной

Стандартным видом многочлена p ( x ) является расположение его одночленов по убыванию степеней его одночленов

где a _n x n — старший член многочлена;

a _n — коэффициент при старшем члене, если a _n ≠ 1, то многочлен называется неприведенным, но если имеется возможность поделить многочлен на a _n , то коэффициент при старшем члене становится равным 1 и многочлен называется приведенным;

a ₀ — свободный член.

Два многочлена равны, когда они имеют одинаковые коэффициенты при одинаковых степенях переменной.

Если многочлен p ( x ) делится на многочлен q ( x ), то в результате получается многочлен s ( x ).

Если многочлен p ( x ) не делится на многочлен q ( x ), то в результате получается многочлен s ( x ) плюс остаток r ( x ), степень которого меньше степени многочлена q ( x ).

При делении многочлена ненулевой степени p ( x ) на двучлен x — a

Вы можете поддержать развитие сайта с помощью платежной формы ниже.

Также Вы можете оплатить консультационные и прочие услуги Ольшевского Андрея Георгиевича