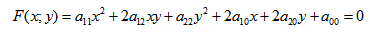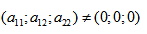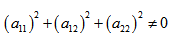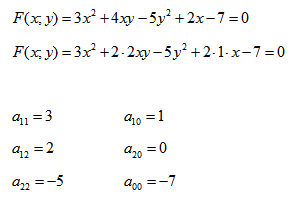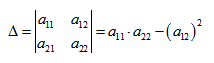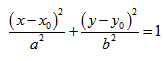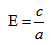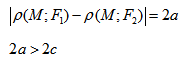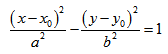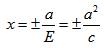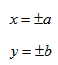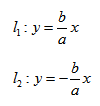Все уравнения кривой и плоскости

VMath

Инструменты сайта

Основное

Навигация

Информация

Действия

Содержание

Касательная, нормальная плоскость, соприкасающаяся плоскость, бинормаль, главная нормаль, репер Френе

Краткие теоретические сведения

Кривая в пространстве

Рассмотрим в пространстве гладкую кривую $\gamma$.

Пусть точка $M$ принадлежит данной кривой и отвечает значению параметра $t=t_0$. Тогда радиус-вектор и координаты данной точки равны:

\begin \vec=\vec(t_0), \quad x_0=x(t_0),\, y_0=y(t_0), \, z_0=z(t_0). \end

Пусть в точке $M$ $ \vec(t_0)\neq\vec<0>$, то есть $M$ не является особой точкой.

Касательная к кривой

Касательная к кривой, проведенная в точке $M$, имеет направляющий вектор коллинеарный вектору $\vec(t_0)$.

Пусть $\vec$ — радиус-вектор произвольной точки касательной, тогда уравнение этой касательной имеет вид

Здесь $\lambda\in(-\infty,+\infty)$ — параметр, определяющий положение точки на касательной (то есть разным значениям $\lambda$ будут соответствовать разные значения $\vec$).

Если $\vec=\$, $M = (x(t_0), y(t_0), z(t_0))$, то можно записать уравнение касательной в каноническом виде:

Нормальная плоскость

Плоскость, проходящую через данную точку $M$ кривой $\gamma$ перпендикулярно касательной в этой точке, называют нормальной плоскостью.

Пусть $\vec$ — радиус-вектор произвольной точки нормальной плоскости, тогда ее уравнение можно записать в векторном виде через скалярное произведение векторов $\vec-\vec(t_0)$ и $\vec(t_0)$:

Если расписать покоординатно, то получим следующее уравнение:

\begin x'(t_0)\cdot(X-x(t_0))+y'(t_0)\cdot(Y-y(t_0))+z'(t_0)\cdot(Z-z(t_0))=0. \end

Соприкасающаяся плоскость

Плоскость, проходящую через заданную точку $M$ кривой $\gamma$ параллельно векторам $\vec(t_0)$, $\vec(t_0)$, когда они неколлинеарны, называют соприкасающейся плоскостью кривой.

Если $\vec$ — радиус-вектор произвольной точки соприкасающейся плоскости, то ее уравнение можно записать через смешанной произведение трех компланарных векторов $\vec-\vec(t_0)$, $\vec(t_0)$, $\vec(t_0)$:

Зная координаты точки и векторов, определяющих плоскость, запишем смешанное произведение через определитель. Получим следующее уравнение соприкасающейся плоскости:

\begin \left| \begin X-x(t_0) & Y-y(t_0) & Z-z(t_0) \\ x'(t_0) & y'(t_0) & z'(t_0)\\ x»(t_0) & y»(t_0) & z»(t_0) \\ \end \right|=0 \end

Бинормаль и главная нормаль

Прямая, проходящая через точку $M$ кривой $\gamma$ перпендикулярно касательной к кривой в этой точке, называется нормалью.

Таких кривых можно провести бесконечно много, все они образуют нормальную плоскость. Мы выделим среди нормалей две — бинормаль и главную нормаль.

Нормаль, перпендикулярную соприкасающейся плоскости, называют бинормалью.

Нормаль, лежащую в соприкасающейся плоскости, называют главной нормалью.

Из определения бинормали (перпендикулярна касательной и перпендикулярна соприкасающейся плоскости) следует, что в качестве ее направляющего вектора мы можем взять векторное произведение $ \vec(t_0)\times\vec(t_0)$, тогда ее уравнение можно записать в виде:

Как и раньше, $\vec$ — радиус-вектор произвольной точки бинормали. Каноническое уравнение прямой:

Из определения главной нормали (перпендикулярна касательной и перпендикулярна бинормали) следует, что в качестве ее направляющего вектора можно взять векторное произведение $\vec(t_0) \times\left[\vec(t_0),\vec(t_0)\right]$:

Уравнение в каноническом виде распишите самостоятельно.

Спрямляющая плоскость

Плоскость, проходящую через заданную точку $M$ кривой $\gamma$ перпендикулярно главной нормали, называют спрямляющей плоскостью.

Другое определение: Плоскость, определяемую касательной к кривой и бинормалью в той же точке, называют спрямляющей плоскостью.

Второе определение позволяет записать уравнение спрямляющей плоскости через смешанное произведение трех компланарных векторов, определяющих эту плоскость $\vec-\vec(t_0)$, $\vec(t_0)$, $\vec(t_0)\times\vec(t_0)$: \begin \left(\vec-\vec(t_0),\, \vec(t_0),\, \vec(t_0)\times\vec(t_0)\right)=0. \end Зная координаты соответствующих векторов, можно легко записать это смешанное произведение через определитель, раскрыв который, вы получите общее уравнение спрямляющей плоскости.

Репер Френе

Орт (то есть единичный вектор) касательной обозначим: $$ \vec<\tau>=\frac<\vec(t_0)><|\vec(t_0)|>. $$ Орт бинормали: $$ \vec<\beta>=\frac<\vec(t_0)\times\vec(t_0)><|\vec(t_0)\times\vec(t_0)|>. $$ Орт главной нормали: $$ \vec<\nu>=\frac<\vec(t_0) \times[\vec(t_0),\,\vec(t_0)]><|\vec(t_0) \times [\vec(t_0),\,\vec(t_0)]|>. $$

Правая тройка векторов $\vec<\tau>$, $\vec<\nu>$, $\vec<\beta>$ называется репером Френе.

Решение задач

Задача 1

Кривая $\gamma$ задана параметрически:

Точка $M$, принадлежащая кривой, соответствует значению параметра $t=0$. Записать уравнения касательной, бинормали, главной нормали, нормальной плоскости, соприкасающейся плоскости и спрямляющей плоскости, проведенных к данной кривой в точке $M$. Записать векторы репера Френе.

Решение задачи 1

Задачу можно решать разными способами, точнее в разном порядке находить уравнения прямых и плоскостей.

Начнем с производных.

\begin 1\cdot X+0\cdot Y+1\cdot (Z-1)=0\,\,\ \Rightarrow \,\, X+Z=1. \end

\begin \left| \begin X-0 & Y-0 & Z-1 \\ 1 & 0 & 1\\ 0 & 2 & 1 \\ \end \right|=0 \end Раскрываем определитель, получаем уравнение: \begin -2X-Y+2Z-2=0 \end

\begin 1\cdot X-4\cdot Y-1\cdot (Z-1)=0\,\,\ \Rightarrow \,\, X-4Y-Z+1=0. \end

Поскольку направляющий вектор главной нормали у нас был найден как векторное произведение направляющих векторов касательной и бинормали, тройка $\vec<\tau>$, $\vec<\nu>$, $\vec<\beta>$ не будет правой (по определению векторного произведения вектор $\vec<\tau>\times\vec<\beta>$ направлен так, что тройка векторов $\vec<\tau>$, $\vec<\beta>$, $\vec<\nu>=\vec<\tau>\times\vec<\beta>$

— правая). Изменим направление одного из векторов. Например, пусть

Теперь тройка $\vec<\tau>$, $\vec<\nu>$, $\vec<\tilde<\beta>>$ образует репер Френе для кривой $\gamma$ в точке $M$.

Задача 2

Написать уравнение соприкасающейся плоскости к кривой $$ x=t,\,\, y=\frac<2>,\,\, z=\frac<3>, $$ проходящей через точку $N(0,0,9)$.

Решение задачи 2

Нетрудно заметить, что точка $N$ не принадлежит заданной кривой $\gamma$. Следовательно соприкасающаяся плоскость проведена в какой-то точке $M(t=t_0)\in\gamma$, но при этом плоскость проходит через заданную точку $N(0,0,9)$.

Найдем значение параметра $t_0$.

Для этого запишем уравнение соприкасающейся плоскости, проведенной в произвольной точке $M(t=t_0)$. И учтем, что координаты $N$ должны удовлетворять полученному уравнению.

Соприкасающаяся плоскость определяется векторами $\vec(t_0)$, $\vec(t_0)$, поэтому записываем определитель \begin \left| \begin X-t_0 & Y-t_0^2/2 & Z-t_0^3/3 \\ &&\\ 1 & t_0 & t^2_0 \\ &&\\ 0 & 1 & 2t_0 \end \right|=0 \quad \Rightarrow \end

\begin (X-t_0)\cdot t_0^2 — (Y-t_0^2/2)\cdot 2t_0 + (Z-t_0^3/3)=0. \end Подставляем вместо $X$, $Y$, $Z$ координаты точки $N$: $X=0$, $Y=0$, $Z=9$, упрощаем и получаем уравнение относительно $t_0$: \begin 9-t_0^3/3=0 \quad \Rightarrow \quad t_0=3. \end Подставив найденное $t_0$ в записанное ранее уравнение, запишем искомое уравнение соприкасающейся плоскости: $$ 9X-6Y+Z-9=0. $$

Задача 3

Через точку $P\left(-\frac45,1,2\right)$ провести плоскость, являющуюся спрямляющей для кривой: $$ x=t^2,\,\, y=1+t,\,\, z=2t. $$

Решение задачи 3

Как и в предыдущей задаче нам неизвестны координаты точки, в которой проведена спрямляющая плоскость к заданной кривой. Найдем их.

Спрямляющая плоскость определяется касательной и бинормалью, то есть векторами $\vec(t_0)$ и $\vec(t_0)\times\vec(t_0)$.

Записываем уравнение спрямляющей плоскости: \begin \left| \begin X-t_0^2 & Y-1-t_0 & Z-2t_0 \\ 2t_0 & 1 & 2\\ 0 & 4 & -2 \end \right|= 0 \end

Раскрываем определитель. Подставляем в уравнение координаты точки $P$: $X=-4/5$, $Y=1$, $Z=2$. Упрощаем и получаем уравнение для нахождения $t_0$: \begin 5t_0^2-8t_0-4=0 \,\, \Rightarrow \,\, t_<01>=2,\, t_<02>=-\frac25. \end

Уравнения соприкасающихся плоскостей к заданной кривой, проходящих через $P$, принимают вид: \begin & 5X-4Y-8Z+24=0,\\ & 25X+4Y+8Z=0. \end

Кривые второго порядка

Кривая второго порядка — это некоторая линия на плоскости, которая в декартовой системе координат задается общим уравнением:

Имеем дело с уравнением второй степени, в котором коэффициенты при старших членах — при вторых степенях одновременно не нули.

или можно встретить следующую форму записи:

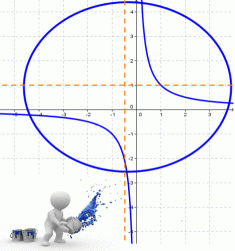
К кривым второго порядка относятся окружность, эллипс, гипербола и парабола.

Покажем на примере определение значений коэффициентов.

Рассмотрим кривую второго порядка:

Вычислим определитель из коэффициентов:

Если Δ = 0, кривая второго порядка параболического типа,

если Δ > 0, кривая второго порядка эллиптического типа,

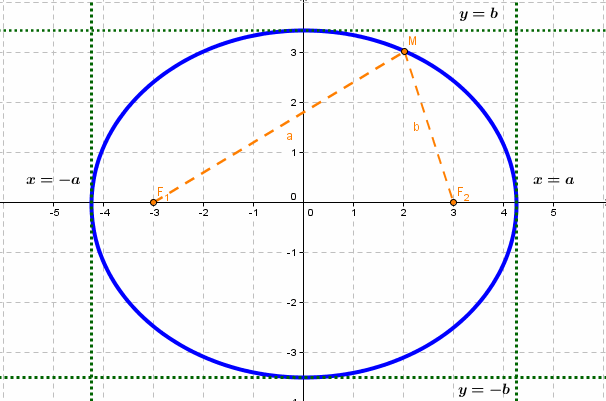
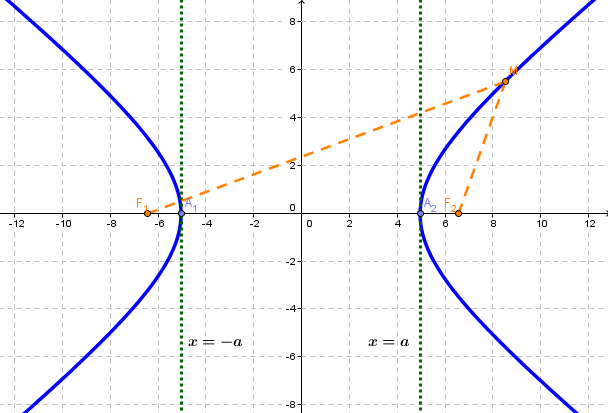
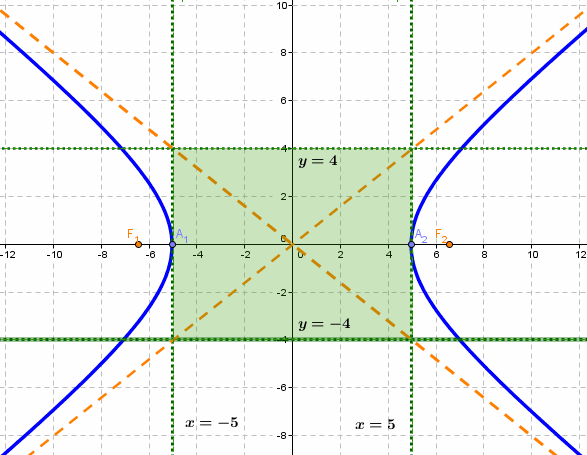
если Δ F₁ и F₂ — фокусы.

с — фокальное расстояние,

Каноническое уравнение эллипса с центром симметрии в начале координат:

2а — большая ось эллипса, 2b — малая ось эллипса.

а — большая полуось эллипса, b — малая полуось эллипса.

Если a = b, то имеем окружность с радиусов R = a = b:

Если центр эллипса находится не в начале координат, а в некоторой точке C(x₀;y₀), оси эллипса параллельны осям координат, то каноническое уравнение эллипса имеет вид:

Эксцентриситет — число, равное отношению фокального расстояния к большей полуоси:

Эксцентриситет характеризует отклонение эллипса от окружности, т.е. чем эксцентриситет больше, тем эллипс более сплющен, вытянут.

Гипербола — множество точек на плоскости для каждой из которых абсолютная величина разности расстояний до двух данных точек F₁ и F₂ есть величина постоянная, меньшая расстояния между этими точками.

с — фокальное расстояние,

Расстояние от центра гиперболы до одного из фокусов называется фокальным расстоянием.

Каноническое уравнение гиперболы с центром симметрии в начале координат:

x — действительная ось, y — мнимая ось.

а — действительная полуось, b — мнимая полуось.

Если центр гиперболы находится в некоторой точке C(x₀;y₀), оси симметрии параллельны осям координат, то каноническое уравнение имеет вид:

Эксцентриситет гиперболы — число, равное отношению фокусного расстояния к действительной полуоси.

Чем эксцентриситет меньше, тем гипербола более вытянута, сплюшена вдоль оси Ох.

Директриса гиперболы — прямые, параллельные мнимой оси гиперболы и отстоящая от нее на расстоянии a/Ε.

f₁ — правая директриса, f₂ — левая директриса.

Порядок построения гиперболы :

1. Строим прямоугольник со сторонами 2a и 2b.

2. Провести асимптоты гиперболы — диагонали построенного прямоугольника.

3. Строим гиперболу с вершинами в точках А 1 (-а;0), А 2 (а;0).

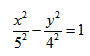Парабола — множество точек на плоскости для каждой из которых расстояние до данной точки F равно расстоянию до данной прямой f.

F — фокус параболы, f — директриса параболы.

Уравнение плоскости, виды уравнения плоскости

В предыдущем разделе, посвященном плоскости в пространстве, мы рассмотрели вопрос с позиции геометрии. Теперь же перейдем к описанию плоскости с помощью уравнений. Взгляд на плоскость со стороны алгебры предполагает рассмотрение основных видов уравнения плоскости в прямоугольной системе координат O х у z трехмерного пространства.

Определение уравнения плоскости

Плоскость – это геометрическая фигура, состоящая из отдельных точек. Каждой точке в трехмерном пространстве соответствуют координаты, которые задаются тремя числами. Уравнение плоскости устанавливает зависимость между координатами всех точек.

Уравнение плоскости в прямоугольной системе координат 0хуz имеет вид уравнения с тремя переменными х , у и z . Удовлетворяют уравнению координаты любой точки, лежащей в пределах заданной плоскости, не удовлетворяют координаты любых других точек, которые лежат вне заданной плоскости.

Подстановка в уравнение плоскости координат точки данной плоскости, обращает уравнение в тождество. При подстановке координат точки, лежащей вне плоскости, уравнение превращается в неверное равенство.

Уравнение плоскости может иметь несколько видов. В зависимости от специфики решаемых задач уравнение плоскости может быть записано по-разному.

Общее уравнение плоскости

Сформулируем теорему, а затем запишем уравнение плоскости.

Всякая плоскость в прямоугольной системе координат O x y z в трехмерном пространстве может быть задана уравнением вида A x + B y + C z + D = 0 , где А , В , С и D – некоторые действительные числа, которые одновременно не равны нулю. Всякое уравнение, имеющее вид A x + B y + C z + D = 0 , определяет плоскость в трехмерном пространстве

Уравнение, имеющее вид A x + B y + C z + D = 0 носит название общего уравнения плоскости. Если не придавать числам А , В , С и D конкретных значений, то мы получаем уравнение плоскости в общем виде.

Важно понимать, что уравнение λ · A x + λ · B y + λ · C z + λ · D = 0 , будет точно так же определять плоскость. В уравнении λ — это некоторое отличное от нуля действительное число. Это значит, что равенства A x + B y + C z + D = 0 и λ · A x + λ · B y + λ · C z + λ · D = 0 равнозначны.

Общим уравнениям плоскости x — 2 · y + 3 · z — 7 = 0 и — 2 · x + 4 · y — 2 3 · z + 14 = 0 удовлетворяют координаты одних и тех же точек, расположенных в трехмерном пространстве. Это значит, что они задают одну и ту же плоскость.

Дадим пояснения к рассмотренной выше теореме. Плоскость и ее уравнение неразделимы, так как каждому уравнению A x + B y + C z + D = 0 соответствует плоскость в заданной прямоугольной системе координат, а каждой плоскости, расположенной в трехмерном пространстве, соответствует ее уравнение вида A x + B y + C z + D = 0 .

Уравнение плоскости A x + B y + C z + D = 0 может быть полным и неполным. Все коэффициенты А , B , С и D в полном уравнении отличны от нуля. В противном случае, общее уравнение плоскости считается неполным.

Плоскости, которые задаются неполными уравнениями, могут быть параллельны координатным осям, проходить через оси координат, совпадать с координатными плоскостями или располагаться параллельно им, проходить через начало координат.

Рассмотрим положение в пространстве плоскости, заданной уравнением 4 · y — 5 · z + 1 = 0 .

Она параллельна оси абсцисс и располагается перпендикулярно по отношению к плоскости O y z . Уравнение z = 0 определяет координатную плоскость O y z , а общее уравнение плоскости вида 3 · x — y + 2 · z = 0 соответствует плоскости, которая проходит через начало координат.

Важное уточнение: коэффициенты А , В и С в общем уравнении плоскости представляют собой координаты нормального вектора плоскости.

Когда говорят об уравнении плоскости, то подразумевают общее уравнение плоскости. Все виды уравнений плоскости, которые мы разберем в следующем разделе статьи, получают из общего уравнения плоскости.

Нормальное уравнение плоскости

Нормальное уравнение плоскости – это общее уравнение плоскости вида A x + B y + C z + D = 0 , которое удовлетворяет следующим условиям: длина вектора n → = ( A , B , C ) равна единице, т.е. n → = A 2 + B 2 + C 2 = 1 , а D ≤ 0 .

Также запись нормального уравнения плоскости может иметь следующий вид cos α · x + cos β · y + cos γ · z — p = 0 , где p – это неотрицательное число, которое равно расстоянию от начала координат до плоскости, а cos α , cos β , cos γ — это направляющие косинусы нормального вектора данной плоскости единичной длины.

n → = ( cos α , cos β , cos γ ) , n → = cos 2 α + cos 2 β + cos 2 γ = 1

То есть, согласно нормальному уравнению плоскости, плоскость в прямоугольной системе координат O х у z удалена от начала координат на расстояние p в положительном направлении нормального вектора этой плоскости n → = ( cos α , cos β , cos γ ) . Если p равно нулю, то плоскость проходит через начало координат.

Плоскость задана общим уравнением плоскости вида — 1 4 · x — 3 4 · y + 6 4 · z — 7 = 0 . D = — 7 ≤ 0 , нормальный вектор этой плоскости n → = — 1 4 , — 3 4 , 6 4 имеет длину, равную единице, так как n → = — 1 4 2 + — 3 4 2 + 6 4 = 1 . Соответственно, это общее уравнение плоскости является нормальным уравнением плоскости.

Для более детального изучения нормального уравнения плоскости мы рекомендуем перейти в соответствующий раздел. В теме приведены разборы задач и характерные примеры, а также способы приведения общего уравнения плоскости к нормальному виду.

Уравнение плоскости в отрезках

Плоскость отсекает на координатных осях O х , O у и O z отрезки определенной длины. Длины отрезков задаются отличными от нуля действительными числами a , b и с . Уравнение плоскости в отрезках имеет вид x a + y b + z c = 1 . Знак чисел а , b и с показывает, в каком направлении от нулевого значения следует откладывать отрезки на координатных осях.

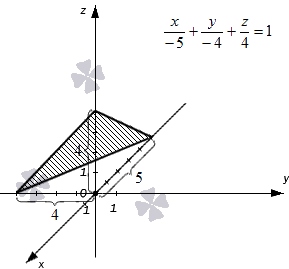
Построим в прямоугольной системе координат плоскость, которая задана уравнением формулы плоскости в отрезках x — 5 + y — 4 + z 4 = 1 .

Точки удалены от начала координат в отрицательном направлении на 5 единиц по оси абсцисс, на 4 единицы в отрицательном направлении по оси ординат и на 4 единицы в положительном направлении по оси аппликат. Отмечаем точки и соединяем их прямыми линиями.

Плоскость полученного треугольника является плоскостью, соответствующей уравнению плоскости в отрезках, имеющего вид x — 5 + y — 4 + z 4 = 1 .

Более подробно информация об уравнении плоскости в отрезках, приведении уравнения плоскости в отрезках к общему уравнению плоскости размещена в отдельной статье. Там же приведен ряд решений задач и примеров по теме.