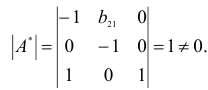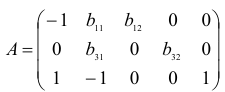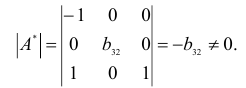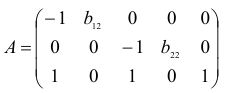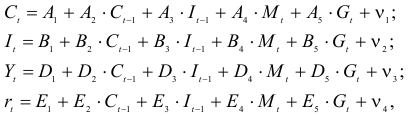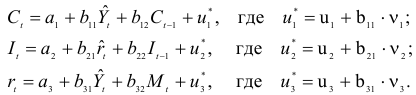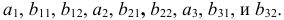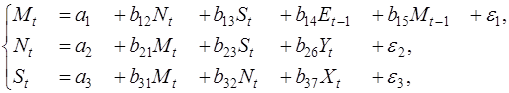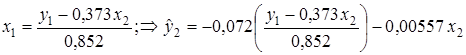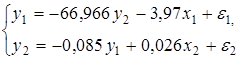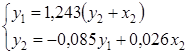Системы эконометрических уравнений
Эконометрика как учебная дисциплина на современном этапе благодаря своей универсальности и возможности практического использования для анализа реальных экономических объектов является одним из базовых курсов в системе высшего экономического образования.
| Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу! |
Эконометрика
Эконометрика — это статистико-математический анализ экономических отношений.
Сущность эконометрики заключается в модельном описании функционирования конкретной экономической системы (экономики данной страны, спроса-предложения в данное время в данном месте и т.д.). Одним из основных этапов эконометрических исследований является анализ устойчивости построенной модели, отражающей взаимосвязи между экономическими показателями, и проверка ее на адекватность реальным экономическим данным и процессам.
Виды систем эконометрических уравнений
Сложные экономические процессы описывают с помощью системы взаимосвязанных (одновременных) уравнений.
Различают несколько видов систем уравнений, применяемых в эконометрике:
• система независимых уравнений — когда каждая зависимая переменная 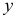
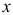
Для построения такой системы и нахождения ее параметров используется метод наименьших квадратов, применяемый к каждому уравнению в отдельности;
• система рекурсивных уравнений — когда зависимая переменная 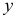
Для построения такой системы и нахождения ее параметров используется метод наименьших квадратов, применяемый последовательно к каждому уравнению в отдельности;
• система взаимосвязанных (совместных) уравнений — когда одни и те же зависимые переменные в одних уравнениях входят в левую часть, а другие в правую:
Такая система уравнений называется структурной формой модели. Для построения таких систем и нахождения их параметров используются косвенный и двухшаговый методы наименьших квадратов.
Возможно эта страница вам будет полезна:
Введем следующие определения:
- Эндогенные переменные — взаимозависимые переменные, которые определяются внутри системы (модели)
.
- Экзогенные переменные — независимые переменные, которые определяются вне системы
.
- Лаговые эндогенные переменные — эндогенные переменные за предыдущие моменты времени.
- Предопределенные переменные — экзогенные и лаговые эндогенные переменные системы.
- Коэффициенты
и
при переменных — структурные коэффициенты модели.
Система линейных функций эндогенных переменных от всех предопределенных переменных системы — приведенная форма модели:
где 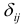
Проблема идентификации
При переходе от приведенной формы модели к структурной исследователь сталкивается с проблемой идентификации. Идентификация -это единственность соответствия между приведенной и структурной формами модели.
С позиции идентифицируемости структурные модели можно подразделить на три вида:
- идентифицируемые;
- неидентифицируемые;
- сверхидентифицируемые.
Модель идентифицируема, если все структурные ее коэффициенты определяются однозначно, единственным образом по коэффициентам приведенной формы модели, т. е. если число параметров структурной модели равно числу параметров приведенной формы модели. В этом случае структурные коэффициенты модели оцениваются через параметры приведенной формы модели и модель идентифицируема.
Модель неидентифицируема, если число приведенных коэффициентов меньше числа структурных коэффициентов, и в результате структурные коэффициенты не могут быть оценены через коэффициенты приведенной формы модели.
Модель еверхидентифицируема, если число приведенных коэффициентов больше числа структурных коэффициентов. В этом случае на основе коэффициентов приведенной формы можно получить два или более значений одного структурного коэффициента. В этой модели число структурных коэффициентов меньше числа коэффициентов приведенной формы.
Сверхидентифицируемая модель, в отличие от неидентифицируемой, модели практически решаема, но требует для этого специальных методов исчисления параметров.
Структурная модель всегда представляет собой систему совместных уравнений, каждое из которых требуется проверять на идентификацию. Модель считается идентифицируемой, если каждое уравнение системы идентифицируемо. Если хотя бы одно из уравнений системы неидентифицируемо, то и вся модель считается неидентифицируемой.
Сверхидентифицируемая модель содержит хотя бы одно сверхидентифицируемое уравнение.
Выполнение условия идентифицируемости модели проверяется для каждого уравнения системы. Чтобы уравнение было идентифицируемо, необходимо, чтобы число предопределенных переменных, отсутствующих в данном уравнении, но присутствующих в системе, было равно числу эндогенных переменных в данном уравнении без одного.
Обозначим через 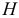
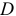
- уравнение идентифицируемо, если
;
- уравнение сверхидентифицируемо, если
;
- уравнение неидентифицируемо, если
.
Если необходимое условие выполнено, то далее проверяется достаточное условие идентификации.
Достаточное условие идентификации — определитель матрицы, составленной из коэффициентов при переменных, отсутствующих в исследуемом уравнении, не равен нулю, и ранг этой матрицы не менее числа эндогенных переменных системы без единицы.
Для решения идентифицируемого уравнения применяется косвенный метод наименьших квадратов, для решения сверхидентифицированных -двухшаговый метод наименьших квадратов.
Косвенный МНК состоит в следующем:
• составляют приведенную форму модели и определяют численные значения ее параметров обычным МНК;
• путем алгебраических преобразований переходят от приведенной формы к уравнениям структурной формы модели, получая тем самым численные оценки структурных параметров.
Двухшаговый МНК заключается в следующем:
• составляют приведенную форму модели и определяют численные значения ее параметров обычным МНК;
• выявляют эндогенные переменные, находящиеся в правой части структурного уравнения, параметры которого определяются двухшаговым МНК, и находят расчетные значения этих эндогенных переменных по соответствующим уравнениям приведенной системы;
• обычным МНК определяют параметры структурного уравнения, используя в качестве исходных данных фактические значения предопределенных переменных и расчетные значения эндогенных переменных, стоящих в правой части уравнения.
Решение эконометрических уравнений
Пример задачи с уравнением №4.2.1.
Рассматривается модель протекционизма Сальватора (упрощенная версия):
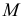
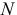
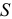
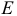
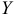
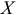
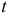
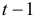
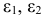
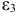
- Применив необходимое и достаточное условие идентификации определить, идентифицировано ли каждое из уравнений модели.
- Определить метод оценки параметров модели.
- Записать приведенную форму модели в общем виде.
Решение:
- Модель представляет с собой систему взаимосвязанных (одновременных) уравнений. Для ответа на вопрос о способе оценки параметров модели проверим каждое ее уравнение на идентификацию.
Модель включает три эндогенные переменные 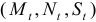
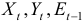
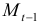
Проверим необходимое условие идентификации для уравнений модели.
Это уравнение включает три эндогенные переменные 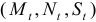
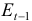
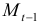
Это уравнение включает три эндогенные переменные 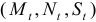
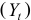
Это уравнение включает три эндогенные переменные 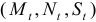
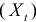
Проверим для каждого из уравнений достаточное условие идентификации. Для этого составим матрицу коэффициентов при переменных модели:
В соответствии с достаточным условием идентификации определитель матрицы коэффициентов, не входящих в исследуемое уравнение, не должен быть равен нулю, а ранг матрицы должен быть не менее, чем число эндогенных переменных модели минус 1, т.е. в данной задаче больше или равен 3-1=2.
Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид
Ранг этой матрицы
Следовательно, для 1 уравнения достаточное условие выполняется, это уравнение точно идентифицируемо. 2 уравнение.
Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид
Ранг этой матрицы
так как она содержит отличный от нуля минор второго порядка
Следовательно, для 2 уравнения достаточное условие выполняется, это уравнение сверхидентифицируемо. 3 уравнение.
Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид
Ранг этой матрицы 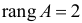
Следовательно, для 3 уравнения достаточное условие выполняется, это уравнение сверхидентифицируемо.
- Таким образом, система в целом сверхидентифицируема, для оценки ее параметров можно применить двухшаговый метод наименьших квадратов.
- Запишем приведенную форму модели в общем виде:
Пример задачи с уравнением №4.2.2.
Рассматривается структурная модель вида:
- Применив необходимое и достаточное условие идентификации определить, идентифицировано ли каждое из уравнений модели.
- Определить метод оценки параметров модели.
- Записать приведенную форму модели в общем виде.
- Исходя из приведенной формы модели уравнений
найти структурные коэффициенты модели.
Решение:
- Модель представляет с собой систему взаимосвязанных (одновременных) уравнений. Для ответа на вопрос о способе оценки параметров модели проверим каждое ее уравнение на идентификацию.
Модель включает три эндогенные переменные 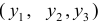
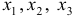
Проверим необходимое условие идентификации для уравнений модели.
Это уравнение включает две эндогенные переменные ( 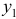
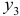
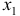
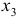
Это уравнение включает три эндогенные переменные 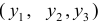
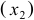
Это уравнение включает две эндогенные переменные (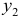
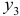
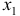
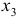
Для этого составим матрицу коэффициентов при переменных модели:
Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид
что не менее чем число эндогенных переменных системы минус один. Следовательно, для первого уравнения достаточное условие идентификации выполнено, уравнение точно идентифицируемо.
Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид
что не менее чем число эндогенных переменных системы минус один. Следовательно, для второго уравнения достаточное условие идентификации выполнено, уравнение точно идентифицируемо.
Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид
что не менее чем число эндогенных переменных системы минус один. Следовательно, для третьего уравнения достаточное условие идентификации выполнено, уравнение точно идентифицируемо.
- Все уравнения системы точно идентифицируемы, следовательно, система в целом точно идентифицируема, для оценки ее параметров может быть применен косвенный метод наименьших квадратов.
- Запишем приведенную форму модели в общем виде:
- Вычисление структурных коэффициентов модели:
1) из третьего уравнения приведенной формы выразим 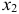
Данное выражение содержит переменные 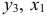
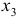
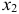
Откуда получим первое уравнение СФМ в виде
2) во втором уравнении СФМ нет переменных 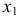

Первый этап: выразим 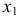
Подстановка данного выражения во второе уравнение ПФМ не решило бы задачу до конца, так как в выражении присутствует 

Подставим его в выражение для
Второй этап: аналогично, чтобы выразить 
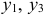
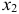

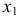
Подставим полученные 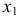

В результате получаем второе уравнение СФМ
3) из второго уравнения ПФМ выразим 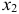
Подставим полученное выражение в третье уравнение ПФМ
В результате получаем третье уравнение СФМ
Таким образом, СФМ примет вид
Пример задачи с уравнением №4.2.3.
Изучается модель вида
где 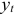
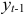
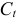
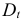
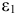
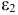
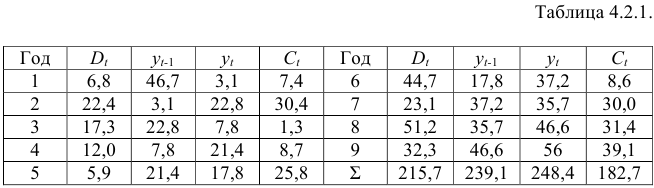
Информация за девять лет о приросте всех показателей дана в таблице 4.2.1.
Для данной модели была получена система приведенных уравнений
- Применив необходимое и достаточное условие идентификации, определить, идентифицировано ли каждое из уравнений модели.
- Рассчитать параметры первого уравнения структурной модели.
Решение:
- В данной модели две эндогенные переменные (
и
) и две экзогенные переменные (
и
). Второе уравнение точно идентифицировано, так как содержит две эндогенные переменные и не содержит одну экзогенную переменную из системы. Иными словами, для второго уравнения имеем по счетному правилу идентификации равенство: 2=1 + 1.
Первое уравнение сверхидентифицировано, так как в нем на параметры при 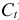
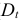
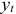
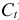
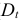
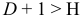
- Для определения параметров сверхидентифицированной модели используется двухшаговый метод наименьших квадратов.
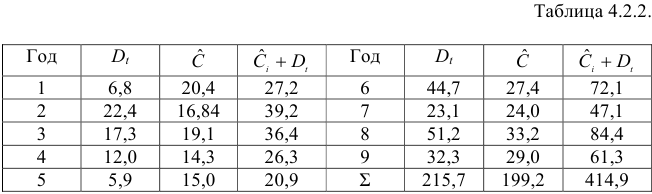
Шаг 1. На основе системы приведенных уравнений по точно идентифицированному второму уравнению определим теоретические значения эндогенной переменной 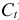
подставим значения 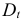
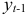
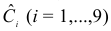
Шаг 2. По сверхидентифицированному уравнению структурной формы модели заменяем фактические значения 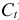
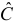
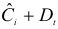
Далее к сверхидентифицированному уравнению применяется метод наименьших квадратов. Обозначим новую переменную 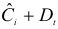
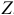
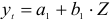
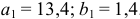
Пример задачи с уравнением №4.2.4.
Рассматривается следующая модель:
— расходы на потребление в период
;
— совокупный доход период
:
— инвестиции в период
;
— процентная ставка в период
;
— денежная масса в период
;
— государственные расходы в период
;
— расходы на потребление в период
;
— инвестиции в период
;
— текущий период;
— предыдущий период;
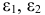
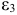
В предположении, что имеются временные ряды данных по всем переменным модели, предложить способ оценки ее параметров.
Как изменится ваш ответ на вопрос п. 1, если из модели исключить тождество дохода?
Решение:
- Модель представляет собой систему одновременных уравнений. Для ответа на вопрос о способе оценки параметров модели проверим каждое ее уравнение на идентификацию.
Модель включает четыре эндогенные переменные 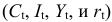
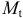
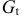
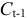
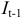
Проверим необходимое условие идентификации для уравнений модели.
Это уравнение включает две эндогенные переменные ( 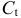
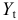
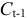
Это уравнение включает две эндогенные переменные 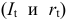
3-е уравнение тоже включает две эндогенные переменные 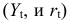
Это уравнение представляет собой тождество, параметры которого известны. Необходимости в его идентификации нет.
Проверим для каждого из уравнений достаточное условие идентификации. Для этого составим матрицу коэффициентов при переменных модели
В соответствии с достаточным условием идентификации определитель матрицы коэффициентов при переменных, не входящих в исследуемое уравнение, не должен быть равен нулю, а ранг матрицы должен быть не менее числа эндогенных переменных модели минус 1, т. е. 4-1=3.
Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид
Ее ранг равен 3, так как определитель квадратной подматрицы 3×3 этой матрицы не равен нулю
Достаточное условие идентификации для 1-го уравнения выполняется.
Выпишем матрицу коэффициентов при переменных, не входящих в уравнение
Ее ранг равен 3, так как определитель квадратной подматрицы 3×3 этой матрицы не равен нулю
Достаточное условие идентификации для 2-го уравнения выполняется.
Выпишем матрицу коэффициентов при переменных, не входящих в уравнение
Ее ранг равен трем, так как имеется квадратная подматрица 3×3 этой матрицы, определитель которой не равен нулю.
Достаточное условие идентификации для 3-го уравнения выполняется.
Таким образом, все уравнения модели сверхидентифицированы. Для оценки параметров каждого из уравнений будем применять двухшаговый МНК.
Шаг 1. Запишем приведенную форму модели в общем виде
где 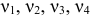
Определим параметры каждого из приведенных выше уравнений в отдельности обычным МНК. Затем найдем расчётные значения эндогенных переменных 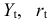
Шаг 2. В исходных структурных уравнениях заменим эндогенные переменные, выступающие в качестве факторных признаков, их расчетными значениями
Применяя к каждому из полученных уравнений в отдельности обычный МНК, определим структурные параметры
Если из модели исключить тождество дохода, число предопределенных переменных модели уменьшится на 1 (из модели будет исключена переменная 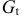
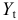
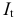
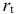
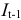
Возможно эти страницы вам будут полезны:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Моделирование структурными уравнениями
8.1. Основные понятия
Наметившийся в последнее время прогресс в области многомерного статистического анализа и анализа корреляционных структур вместе с новейшими вычислительными алгоритмами послужил отправной точкой для создания новой, но уже получившей признание техники моделирования структурными уравнениями (SEPATH). Эта по сути всеобъемлющая и необычайно мощная техника многомерного анализа включает большое количество методов из различных областей статистики.
Кратко можно сказать, что SEPATH представляет собой весьма серьезное развитие многих методов многомерного анализа. Именно здесь получили естественное развитие и были объединены множественная регрессия и факторный анализ . Основными задачами, для решения которых используются структурные уравнения, являются:
причинное моделирование, или анализ путей, при проведении которого предполагается, что между переменными имеются причинные взаимосвязи. Возможна проверка гипотез и подгонка параметров причинной модели, описываемой линейными уравнениями. Причинные модели могут включать явные или латентные переменные, а также те и другие одновременно;
подтверждающий факторный анализ, используемый в развитие обычного факторного анализа для проверки определенных гипотез о структуре факторных нагрузок и корреляций между факторами;
факторный анализ второго порядка, являющийся модификацией факторного анализа, при проведении которого для получения факторов второго порядка анализируется корреляционная матрица общих факторов;
построение регрессионных моделей, что является модификацией многомерного линейного регрессионного анализа, при котором коэффициенты регрессии могут быть зафиксированы равными друг другу или каким-нибудь заданным значениям;
моделирование ковариационной структуры, позволяющее проверить гипотезу о том, что матрица ковариации имеет определенный вид. Например, с помощью этой процедуры можно проверить гипотезу о равенстве дисперсий у всех переменных;
построение моделей корреляционной структуры, которое позволяет проверить гипотезу о том, что матрица корреляции имеет определенный вид. Классическим примером является гипотеза о том, что матрица корреляции имеет циклическую структуру;
построение моделей структуры средних, которые позволяют исследовать структуру средних, например, одновременно с анализом дисперсий и ковариаций.
Поскольку многие виды моделей подпадают сразу под несколько из названных категорий, при практическом анализе структурной модели ее довольно сложно классифицировать. Впрочем, в этом нет особой необходимости.
Структурные уравнения, включающие только линейные связи между явными и латентными переменными, могут быть изображены в виде диаграмм путей. Поэтому даже начинающий пользователь может провести сложный анализ с минимальными затратами времени на обучение.
8.2. Основы структурного моделирования
Одной из основных идей структурного моделирования, со знакомства с которой начинается изучение статистики, является эффект воздействия аддитивных и мультипликативных преобразований. Студентов учат, что если умножить каждое число на некоторую константу 


Таким образом, если мы имеем набор чисел 

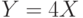




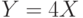


Эта идея может быть различными способами распространена на несколько переменных, связанных системой линейных уравнений. При этом правила преобразований становятся более громоздкими, а вычисления более сложными. Но основной смысл остается прежним: проверить, связаны ли переменные линейной зависимостью, можно, изучая их дисперсии и ковариации.
Чтобы проверить, имеет ли ковариационная матрица заданную структуру, статистики используют несколько процедур. Процесс структурного моделирования включает в себя следующие этапы:
- исследователь (пользователь) описывает (обычно с помощью диаграммы путей) модель, представляющую его понимание зависимостей между переменными;
- программа с помощью специальных внутренних методов определяет, какие значения дисперсий и ковариаций переменных получаются в текущей модели на основании входных данных;
- программа проверяет, насколько хорошо полученные дисперсии и ковариации отвечают данной модели;
- программа сообщает пользователю полученные результаты статистических испытаний, а также выводит оценки параметров и стандартные ошибки для численных коэффициентов в линейных уравнениях и одновременно выдает большое количество дополнительной диагностической информации;
- на основании этой информации пользователь решает, хорошо ли текущая модель согласуется с его данными.
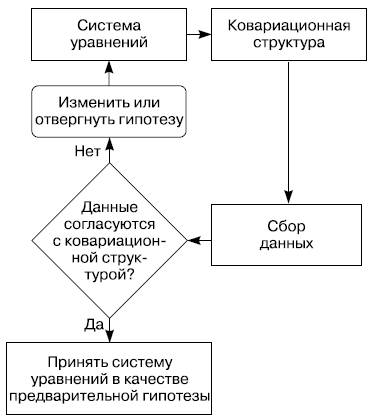
Последовательность процесса структурного моделирования можно представить в виде блок-схемы (рис. 8.1).
Хотя логика математических вычислений при проведении структурного моделирования очень сложна, основные этапы соответствуют пяти шагам на схеме (см. рис. 8.1). Однако следует помнить, что по ряду причин не разумно ожидать идеального соответствия модели и данных. Структурные модели с линейными зависимостями являются только приближениями реальных явлений. Природные зависимости далеки от линейных. Поэтому истинные зависимости между переменными скорее всего не линейны. Более того, истинность многих статистических предположений, накладываемых на проверяемую модель, остается под большим вопросом.
На практике важна не идеальность согласованности модели с данными, а ее пригодность для практического использования и разумного объяснения структуры наблюдаемых данных. Кроме того, следует помнить, что идеальное соответствие модели данным не обязательно означает, что модель верна. Возможно, существует другая модель, которая ничуть не хуже согласуется с теми же данными. И вообще, умение доказывать правильность модели эквивалентно умению предсказывать будущее.
Оценивание параметров структурной модели
Структурная и приведенная формы модели.
Система одновременных уравнений (т.е. структурная форма модели) обычно содержит эндогенные и экзогенные переменные.
Эндогенные переменные –это зависимые переменные, число которых равно числу уравнений в системе. Они обозначаются через y
Экзогенные переменные –это предопределенные переменные, влияющие на эндогенные переменные, но не зависящие от них. Они обозначаются через x.
Простейшая структурная форма модели имеет вид:
Классификация переменных на эндогенные и экзогенные зависит от теоретической концепции принятой модели. Экономические переменные могут выступать в одних моделях как эндогенные, а в других — как экзогенные переменные. Внеэкономические переменные (например, климатические условия) входят в систему как экзогенные переменные. В качестве экзогенных переменных можно рассматривать значения эндогенных переменных за предшествующий период времени (лаговые переменные). Например, потребление текущего года yt может зависеть также и от уровня потребления в предыдущем году yt-1.
Структурная форма модели позволяет увидеть влияние изменений любой экзогенной переменной на значения эндогенной переменной. Целесообразно в качестве экзогенных переменных выбирать такие переменные, которые могут быть объектом регулирования. Меняя их и управляя ими, можно заранее иметь целевые значения эндогенных переменных.
Коэффициенты 



Использование МНК для оценивания структурных коэффициентов модели дает смещенные и несостоятельные оценки. Поэтому обычно для определения структурных коэффициентов модели структурная форма преобразуется в приведенную.
Приведенная форма моделипредставляет собой систему линейных функций эндогенных переменных от экзогенных:


По своему виду приведенная форма модели ничем не отличается от системы независимых уравнений, Применяя МНК, можно оценить 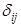
Приведенная форма позволяет выразить значения эндогенных переменных через экзогенные, однако аналитически уступает структурной форме модели, т.к. в ней отсутствуют оценки взаимосвязи между эндогенными переменными.
Проблема идентификации
При переходе от приведенной формы модели к структурной исследователь сталкивается с проблемой идентификации. Идентификация –это единственность соответствия между приведенной и структурной формами модели.
Структурная модель (2) в полном виде, состоящая в каждом уравнении системы из n эндогенных и m экзогенных переменных, содержит n(n-1+m) параметров. Приведенная модель (3) в полном виде содержит nm параметров. Таким образом, в полном виде структурная модель содержит большее число параметров, чем приведенная форма модели. Поэтому n(n-1+m) параметров структурной модели не могут быть однозначно определены через nm параметров приведенной формы модели.
Чтобы получить единственно возможное решение для структурной модели, необходимо предположить, что некоторые из структурных коэффициентов модели равны нулю. Тем самым уменьшится число структурных коэффициентов.
С позиции идентифицируемости структурные модели можно подразделить на три вида:
Модель идентифицируема,если все структурные ее коэффициенты определяются однозначно, единственным образом по коэффициентам приведенной формы модели, т.е. число параметров структурной модели равно числу параметров приведенной формы модели.
Модель неидентифицируема,если число приведенных коэффициентов меньше числа структурных коэффициентов, и в результате структурные коэффициенты не могут быть оценены через коэффициенты приведенной формы модели. Модель (2) в полном виде всегда неидентифицируема.
Модель сверхидентифицируема,если число приведенных коэффициентов больше числа структурных коэффициентов. В этом случае на основе приведенных коэффициентов можно получить два или более значений одного структурного коэффициента. Сверхидентифицируемая модель, в отличие от неидентифицируемой, практически решаема, но требует для этого специальных методов исчисления параметров.
Структурная модель всегда представляет собой систему совместных уравнений, каждое из которых требуется проверять на идентификацию. Модель считается идентифицируемой, если каждое уравнение системы идентифицируемо.Если хотя бы одно из уравнений системы неидентифицируемо, то и вся модель считается неидентифицируемой. Сверхидентифицируемая модель содержит хотя бы одно сверхидентифицируемое уравнение.
Обозначим Н – число эндогенных переменных в i— ом уравнении системы, D – число экзогенных переменных, которые содержатся в системе, но не входят в данное уравнение. Тогда условие идентифицируемости уравнения может быть записано в виде следующего счетного правила:
D+1 = Н – уравнение идентифицируемо;
D+1 Н – уравнение сверхидентифицируемо.
Это счетное правило отражает необходимое, но не достаточное условие идентификации. Более точно условия идентификации определяются, если накладывать ограничения на коэффициенты матриц параметров структурной модели. Уравнение идентифицируемо, если по отсутствующим в нем переменным (эндогенным и экзогенным) можно из коэффициентов при них в других уравнениях системы получить матрицу, определитель которой не равен нулю, а ранг матрицы не меньше, чем число эндогенных переменных в системе без одного.
Пример. Рассмотрим следующую макроэкономическую модель:
где M – доля импорта в ВВП;
N – общее число прошений об освобождении от таможенных пошлин;
S – число удовлетворенных прошений;
E – фиктивная переменная, означающая, является ли курс доллара искусственно завышенным или нет;
Y – реальный ВВП;
X – реальный объём чистого экспорта;
t – текущий период;
t-1 – предыдущий период.
Проверим данную модель на идентификацию и определим, каким методом могут быть рассчитаны её коэффициенты (в случае, если модель сверх – или точно идентифицируема).
Сначала рассмотрим общие характеристики структурной формы. Здесь три эндогенные переменные – Mt, Nt и St, они стоят в левых частях уравнений. Кроме того, в правых частях находятся четыре предопределенные переменные – одна лаговая (Mt-1) и три экзогенные – Et-1, Yt и Xt. Теперь проверим каждое уравнение.
Уравнение I. В этом уравнении присутствуют три эндогенные переменные (Mt, Nt и St), но отсутствуют две предопределенные переменные — Yt и Xt. Поэтому Н=3, D=2, и необходимое условие идентификации выполняется, поскольку D+1=H. Это означает, что первое уравнение точно идентифицируемо.
Уравнение II. В этом уравнении присутствуют три эндогенные переменные (Mt, Nt и St), но отсутствуют три экзогенные — Еt—1, Mt-1 и Xt. Поэтому Н=3, D=3, D+1>H и второе уравнение по необходимому условию является сверхидентифицируемым.
Уравнение III. В этом уравнении, как и в других уравнениях, присутствуют все три эндогенные переменные, но отсутствуют три экзогенные — Еt—1, Mt-1 и Yt . Поэтому Н=3, D=3, D+1>H, и третье уравнение системы является сверхидентифицируемым.
Проверим каждое уравнение на выполнение достаточного условия идентификации. Для этого сначала запишем расширенную матрицу системы в виде следующей таблицы:
| Уравнение | Mt | Nt | St | Et-1 | Mt-1 | Yt | Xt |
| I | -1 | b12 | b13 | b14 | b15 | ||
| II | b21 | -1 | b23 | b26 | |||
| III | b31 | b32 | -1 | b37 |
Как видим, в эту матрицу включены коэффициенты при всех переменных и не включены свободные члены, поскольку они могут быть исключены из системы, если задавать все переменные в отклонениях от среднего значения. Кроме того, здесь все переменные перенесены в правые части уравнений.
Достаточное условие идентификации для соответствующего уравнения будет выполнено, если ранг подматрицы, построенной только из коэффициентов при переменных, отсутствующих в этом уравнении, равен количеству эндогенных переменных в системе минус единица.
Рассмотрим подробно этот процесс для первого уравнения системы. Первому уравнению соответствует первая строка расширенной матрицы, поэтому первую строку не следует включать в подматрицу. Из остальной части расширенной матрицы оставим только столбцы, которые имеют нули в первой строке. Получаем подматрицу:

определитель которой не равен нулю, поскольку 
Аналогично рассмотрим другие уравнения. Подматрица для второго уравнения имеет вид:

Её ранг также равен двум, поскольку определитель, составленный, например, из первого и третьего столбцов, очевидно, не равен нулю.
Подматрица для третьего уравнения имеет вид:

Она также имеет ранг, равный двум.
Таким образом, достаточное условие идентификации выполнено для каждого уравнения системы. Поскольку среди уравнений системы нет неидентифицируемых, а второе и третье уравнения являются сверхидентифицированными, то и модель в целом сверхидентифицирована. Для определения параметров первого уравнения должен быть применен косвенный МНК (поскольку оно точно идентифицировано), а для других уравнений – двухшаговый МНК.
Приведенная форма модели имеет вид:
Здесь 
Оценивание параметров структурной модели
Коэффициенты структурной модели могут быть оценены разными способами в зависимости от вида системы одновременных уравнений. Наибольшее распространение получили два метода оценивания коэффициентов структурной модели: косвенный МНКи двухшаговый МНК.
Косвенный МНК (КМНК) применим в случае точно идентифицируемой структурной модели. Процедура следующая:
1. Структурная модель преобразуется в приведенную форму.
2. Для каждого уравнения приведенной формы обычным МНК оцениваются коэффициенты δij
3. Коэффициенты приведенной модели трансформируются в параметры структурной модели.
Рассмотрим применение КМНК для модели:
Для построения модели имеем таблицу:
| № п/п |  |  |  |  |
| Средние | 6,2 | 2,4 | 3,4 |
Приведенная форма модели имеет вид:
где 
Для каждого уравнения приведенной формы применим традиционный МНК и определим δ— коэффициенты. Для простоты работаем в отклонениях, т.е. 
Для приведенных данных система составит:
Отсюда получаем первое уравнение ( и аналогично второе):
Перейдем к структурной форме следующим образом: исключим из первого уравнения приведенной формы x2 , выразив его из второго уравнения приведенной формы и подставив в первое уравнение:
Первое уравнение структурной формы:
Аналогично исключим из второго уравнения x1 выразив его через первое уравнение и подставив во второе:

Структурная форма модели имеет вид:
Эту же систему можно записать, включив в нее свободный член уравнения, т.е. перейти от переменных в виде отклонений от среднего к исходным переменным 
Тогда структурная модель имеет вид:
Если к каждому уравнению структурной формы применить традиционный МНК, то результаты могут сильно отличаться. В данном примере будет:
Двухшаговый МНК.ДМНК используется для сверхидентифицируемых систем. Основная идея ДМНК: на основе приведенной формы модели получить для сверхидентифицируемого уравнения теоретические значения эндогенных переменных, содержащихся в правой части уравнения. Далее, подставив их вместо фактических значений, можно применить обычный МНК к структурной форме сверхидентифицируемого уравнения. Здесь дважды используется МНК: на первом шаге при определении приведенной формы модели и нахождении на ее основе оценок теоретических значений эндогенной переменной 
Сверхидентифицируемая структурная модель может быть двух типов:
— все уравнения системы сверхидентифицируемые;
— система содержит также точно идентифицируемые уравнения.
В первом случае для оценки структурных коэффициентов каждого уравнения используется ДМНК. Во втором случае структурные коэффициенты для точно идентифицируемых уравнений находятся из системы приведенных уравнений.
Она получена из предыдущего примера наложением ограничения 
На первом шаге найдем приведенную форму модели. С использованием тех же исходных данных получим систему:
На основе второго уравнения этой системы можно найти теоретические значения для эндогенной переменной 

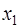

 |  | 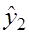 |  |  |  |  |
| -1,4 | -0,4 | 0,103 | -1,297 | -2 | 2,594 | 1,682 |
| -0,4 | -2,4 | 0,042 | -0,358 | -1 | 0,358 | 0,128 |
| 0,6 | -1,4 | -0,035 | 0,565 | 0,319 | ||
| -0,4 | 1,6 | 0,02 | -0,38 | -0,38 | 0,144 | |
| 1,6 | 2,6 | -0,13 | 1,47 | 2,94 | 2,161 | |
| 5,512 | 4,434 |
После того, как найдены оценки 

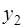



В целом рассматриваемая система будет иметь вид:
Второе уравнение не изменилось по сравнению с предыдущим примером.
ДМНК является наиболее общим и широко распространенным методом решения системы одновременных уравнений. Для точно идентифицируемых уравнений ДМНК дает тот же результат, что и КМНК.
http://intuit.ru/studies/courses/3545/787/lecture/30355
http://poisk-ru.ru/s25199t11.html

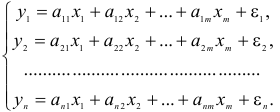
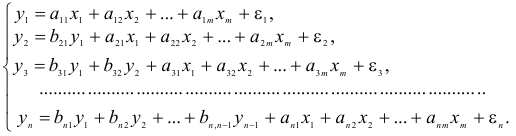
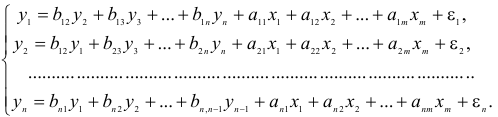
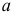 и
и 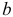 при переменных — структурные коэффициенты модели.
при переменных — структурные коэффициенты модели.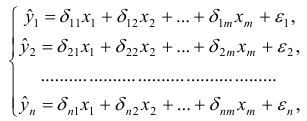
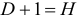 ;
;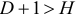 ;
;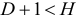 .
.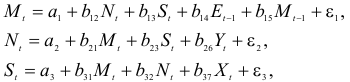

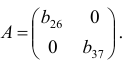
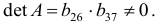
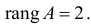
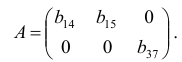
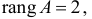
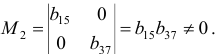
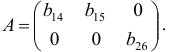
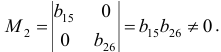
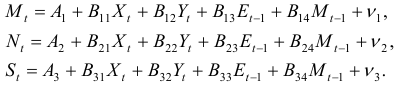
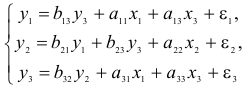
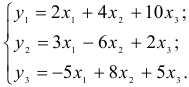

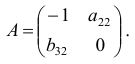
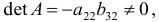
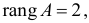
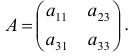
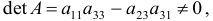
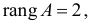
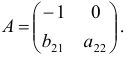
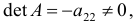
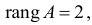
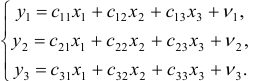
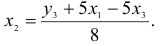
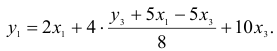
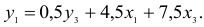
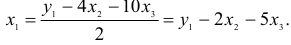
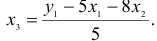
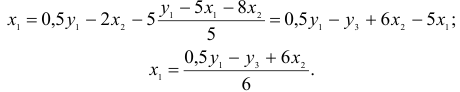
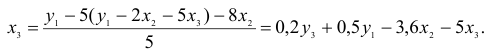
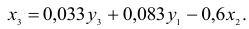
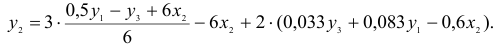
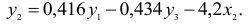
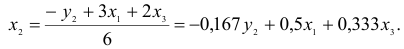
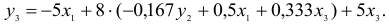
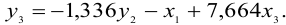
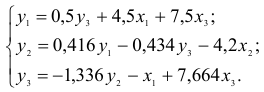
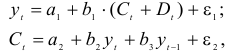
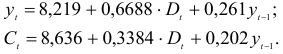
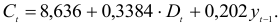
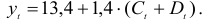
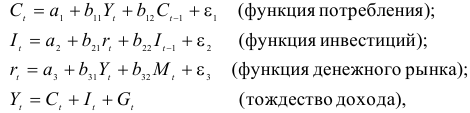
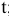 ;
;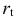 — процентная ставка в период
— процентная ставка в период 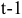 ;
;