Исследовательская работа по математике обучающейся 11 класса Петряевой Марии на тему «Матрицы. Решение систем линейных уравнений»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Научно — практическая конференция «Первые шаги в науку»
Матрицы. Решение систем линейных уравнений
Автор работы: Петряева Мария Савровна
Место выполнения работы: РК, Яшалтинский р-н, с. Яшалта,
МКОУ «Яшалтинская СОШ имени В. А. Панченко»
Руководитель : Точка И. Г. , учитель математики.
Глава 1. Матрицы. Действия с матрицами ____________________________ 5
Основные сведения о матрицах_______________________________ 5
1.2 Операции над матрицами_______________________________ ______ 6
Глава 2. Определители. Метод Крамера. Решение систем линейных уравнений.______________________________________________________ 7
2.1 Определители. Способы вычисления определителей . ___________ ____7
2.2 Решение систем линейных уравнений методом Крамера ._________ ____ 9
Глава 3. Обратная матрица. Решение систем линейных уравнений с помощью обратной матрицы._______________________________________10
Глава 4. Метод Гаусса решения систем линейных уравнений.____________11
4.1 Ранг матрицы и его вычисление__________________________________11
4.2 Теорема Кронекера-Капелли.____________________________________12
4.3 Метод Гаусса__________________________________________________13
Глава 5 . Практикум по решению систем линейных уравнений различными способами. Применение матричного исчисления для решения экономических задач ________________________________________________________14
Список литературы ___________________________________________ 29
Приложение _________________________________________________ 30
Обоснование выбора темы: Посмотрев фильм 2017 года «Матрица времени», я поняла, что слышу понятие матрицы довольно часто, но не знаю, что оно означает. И вот у меня возник вопрос: «Что такое матрица?». Поискав нужное определение в интернете, я узнала, что это математическое понятие, и меня это очень порадовало, потому что математика была всегда интересна мне. Изучив это понятие глубже, я увидела некую связь с темой «Массивы» в информатике, а также выяснила, что с помощью матриц можно решать системы линейных уравнений с произвольным количеством переменных и уравнений. В школьном курсе мы изучали способы решения систем уравнений: способ подстановки, сложения, графический. При этом разбирали системы с двумя неизвестными. Теперь в задачнике встретились системы с тремя неизвестными, т.е. они стали сложнее, поэтому возникла проблема, найти для себя способ решения систем удобный, короткий, универсальный. Кроме того, я нашла непосредственно примеры применения линейной алгебры при решении экономических задач.
Поэтому мой интерес к матрицам усилился. Именно поэтому я решила более детально изучить тему, которая затрагивает два моих любимых предмета: математику и информатику.
Цели и задачи исследования:
1. Познакомиться с понятием «Матрица».
2. Изучить возможные операции над матрицами.
3. Научиться решать системы линейных уравнений разными способами.
4 . Рассмотреть применение матриц в жизни человека.
Новизна исследования : написание программы на языке программирования Pascal для решения систем линейных уравнений.
Практическая значимость : полученные мною знания пригодятся мне в дальнейшем изучении математики, так как я планирую продолжить обучение в ВУЗе, где математика будет ведущим предметом. Также подобранный мною материал пригодится ученикам и учителям для расширения математического кругозора школьников.
Гипотеза: возможно ли ученикам средней школы воспринять материал, который студенты изучают на первом курсе университетов.
Актуальность: Сегодня любому квалифицированному экономисту, финансисту, логисту, статисту просто необходима мощная математическая база. Для них, одним из главных предметов в высшей математике является линейная алгебра, а именно матричная алгебра. Именно она является наиболее компактной и удобной для решения многих поставленных задач. Матричные методы все чаще применяются на практике: различные виды статистических расчётов, сокращение документооборота, организация внутри производства хозяйственных расчётов и экономико-математического анализа. Поэтому, выполнив свою работу, я получу полезные знания, которые, уверенна, пригодятся мне в будущем.
Объект исследования : матрицы
Предмет исследования: способы решения систем линейных уравнений.
Методы исследования : анализ, синтез, сравнение.
ГЛАВА 1.МАТРИЦЫ. ДЕЙСТВИЯ С МАТРИЦАМИ
1.1. Основные сведения о матрицах .
Матрицей размерности m×n называется совокупность чисел, расположенных в виде таблицы, содержащей m строк и n столбцов:
где a ij ∈ R (i=1,2. m; j=1,2. n).
Числа ij a называются элементами матрицы . Индекс i– номер строки (он всегда стоит на первом месте), j– номер столбца.
Матрицы обозначаются прописными (заглавными) буквами латинского алфавита, в сокращённой записи:
A= (a ij ); i =1, 2, …, m; j =1, 2, …, n. Например: A 2×3 =
Если матрица состоит из одной строки, то она называется матрицей–строкой размерности 1×n:
Если матрица состоит из одного столбца, то она называется матрицей–столбцом размерности m×1:
При n=m матрица (1) называется квадратной матрицей n–го порядка.
Элементы матрицы ij a , у которых номер строки равен номеру
столбца (i=j), называются диагональными и образуют главную диагональ матрицы.
Если все недиагональные элементы квадратной матрицы равны нулю, то матрица называется диагональной.
Если у диагональной матрицы n–го порядка все диагональные элементы равны единице, то матрица называется единичной матрицей n–го порядка, она обозначается E.
Матрица любого размера называется нулевой , или нуль–матрицей , если все её элементы равны нулю: O = .
1.2. Операции над матрицами
Над матрицами, как и над числами, можно производить ряд операций, причём некоторые из них аналогичны операциям над числами, а некоторые специфические.
1. Умножение матрицы на число. Произведением матрицы А на
число λ (l ∈ R) называется матрица B = λ ⋅ A с элементами b ij = λ ⋅ a ij для i =1,2, . m,;
j =1,2. n, (размерности матриц А и В одинаковые).
Следствие. Общий множитель всех элементов матрицы можно
выносить за знак матрицы.
Матрица (–1) ⋅ А называется противоположной матрице А и обозначается –А.
2. Сложение матриц. Суммой двух матриц А и В одинаковой размерности m×n называется матрица С=А+В размерности m×n, элементы которой определяются равенствами c ij = a ij + b ij для всех значений индексов i и j (т.е. две матрицы складываются поэлементно). В
частном случае A = A + 0 , где 0– нулевая матрица.
3. Вычитание матриц. Разностью двух матриц А и В одинаковой размерности m×n называется матрица С=А+(–1) ⋅ В той же размерности, если для всех значений индексов i, j выполнены равенства c ij = a ij –b ij , (т.е. две матрицы вычитаются поэлементно).
4. Умножение матриц. Умножение матрицы А на матрицу В определено, когда число столбцов первой матрицы равно числу строк второй. Тогда произведением матриц A ⋅ B называется такая m × k k × n матрица C m × n , каждый элемент которой равен сумме произведений соответствующих элементов i –й строки первой матрицы на элементы j –го столбца второй матрицы: c ij = a i 1 ⋅ b 1 j + a i 2 ⋅ b 2 j +. + a ik ⋅ b kj , где i =1, 2, …, m ; j =1, 2, …, n .
5. Транспонирование матриц. Транспонирование – переход от матрицы А к матрице A T , в которой строки и столбцы поменялись местами с сохранением порядка. Матрица A T называется транспонированной относительно матрицы А.
ГЛАВА 2.ОПРЕДЕЛИТЕЛИ. МЕТОД КРАМЕРА. РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ.
2.1 Определители. Способы вычисления определителей.
Определителем матрицы первого порядка А= (а ij ) называется элемент а 11 .
Обозначают определитель матрицы А как : Δ, det , │А│.
Определителем матрицы второго порядка А=( а ij ) называется число , которое вычисляется по формуле:
Определителем матрицы третьего порядка А= (а ij ) называется число, которое вычисляют по формуле:
Знаки, с которыми члены определителя входят в формулу легко запомнить, пользуясь схемой ,которой называется «правилом треугольников».
Определитель не изменится , если строки определителя заменить столбцами, а столбцы- соответствующими строками.
Общий множитель всех элементов какой-нибудь строки (или столбца) можно выносить за знак определителя
Определитель с двумя одинаковыми строками (столбцами ) равен нулю.
При перестановке двух строк (столбцов) определитель меняет свой знак на противоположный.
Определитель с двумя пропорциональными строками (столбцами) равен нулю.
Определитель не изменится, если к элементам одной строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженных на одно и то же число.
Определителем квадратной матрицы n -го порядка называется число, равное алгебраической сумме n ! Членов, каждый из которых является произведением n элементов матрицы, взятых по одному из каждой строки и и каждого столбца.
На практике расчет определителей n -го порядка удобнее вести с помощью разложения по элементам строки или столбца. Для использования этого метода введем определения минора и алгебраического дополнения.
Минором М ij элемента a ij матрицы n –порядка называется определитель матрицы ( n -1)-го порядка, полученной из матрицы А вычеркиванием i -строки и j -го столбца. Каждая матрица n -го порядка имеет n 2 миноров ( n -1)-го порядка.
Алгебраическим дополнением А ij элемента a ij матрицы n –порядка называется соответствующий этому элементу минор, умноженный на
Теорема разложения. Определитель квадратной матрицы равен сумме произведений элементов любой строки или любого столбца на соответствующее им алгебраическое дополнения.
2.2 Решение систем линейных уравнений методом Крамера.
С помощью определителей очень удобно записывать решение СЛУ. Рассмотрим систему трех линейных уравнений с тремя неизвестными.
Обозначим Δ –определитель , составленный из коэффициентов при неизвестных, такой определитель называется главным определителем системы.
Если Δǂ 0, система имеет единственное решение, которое определяется по формулам:
т. е. определители Δ 1 , Δ 2 , Δ 3 получаются из определителя Δ путем замены его первого, второго и третьего столбцов столбцом свободных членов.
Формулы (*) называются формулами Крамера.
Эти же формулы обобщаются и на систему n линейных уравнений с n неизвестными.
ГЛАВА 3. ОБРАТНАЯ МАТРИЦА. РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ С ПОМОЩЬЮ ОБРАТНОЙ МАТРИЦЫ.
Пусть матрица А невырожденная матрица, т. е. ее определитель не равен нулю. Матрица А -1 , удовлетворяющая условию: А*А -1 = Е, называется обратной матрицей.
Формула расчета обратной матрицы имеет вид:
С помощью обратной матрицы можно находить решения СЛУ.
Пусть требуется решить систему из n линейных уравнений с n неизвестными:
Введем обозначение матриц:
Найдем решение системы уравнений в матричной форме: используя правило умножения матриц и условие равенства матриц, систему уравнений можно представить в виде:
Таким образом, чтобы найти матрицу неизвестных Х, достаточно найти матрицу А -1 и умножить ее на матрицу свободных членов В.
ГЛАВА4. МЕТОД ГАУССА РЕШЕНИЙ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ.
4.1 Ранг матрицы и его вычисление
В матрице А размера mxn вычеркиванием каких-либо строк или столбцов можно вычленить квадратные матрицы k -го порядка, где k ≤ min ( m ; n ). Определители таких подматриц называют минорами k -го порядка матрицы А.
Рангом матрицы А называется наибольший порядок отличных от нуля миноров этой матрицы.
Ранг матрицы А обозначают rangA или r ( A ) . Из определения матрицы следует:
А) ранг матрицы А mxn не превосходит меньшего из ее размеров ;
Б) r ( A )=0 тогда и только тогда, когда все элементы матрицы равны нулю.
В) для квадратной матрицы n -го порядка r ( A )= n тогда и только тогда, когда матрица А – невырожденная.
В общем случае определение ранга матрицы перебором всех миноров достаточно трудоемко. Для облегчения этой задачи используются элементарные преобразования матрицы:
Вычеркивание нулевой строки (столбца);
Умножение всех элементов строки (столбца) матрицы на число, не равное нулю;
Изменение порядка строк (столбцов)
Прибавление к каждому элементу одной строки (столбца) соответствующих элементов другой строки (столбца), умноженных на число, отличное от нуля;
В результате таких преобразований исходную матрицу можно преобразовать в единичную. Число единиц на главной диагонали равно рангу этой матрицы.
4.2 Теорема Кронекера-Капелли.
Нахождение ранга матрицы позволяет упростить решение СЛУ.
Рассмотрим систему m линейных уравнений с n неизвестными:
C истема уравнений называется совместной , если она имеет хотя бы одно решение. Если система не имеет решений, то она называется несовместной .
Система называется определенной , если она имеет только одно решение, и неопределенной если таких решений несколько.
называются соответственно основной матрицей и расширенной матрицей системы уравнений. Очевидно, что rang A ≤ rangB .
Теорема Кронекера- Капелли: система линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы А равен рангу расширенной матрицы В этой системы.
Из теоремы Кронекера- Капелли следует, что :
Если ранг матрицы совместной системы равен числу переменных, то система является определенной и имеет единственное решение, т. е.
Если ранг матрицы совместной системы меньше числа переменных, то система неопределенная и имеет бесконечное множество решений,
т. е. r ( A )= r (В) n .
3. Если r ( A ) r (В) , то система несовместна и решений не имеет.
С помощью элементарных преобразований строк расширенная (и одновременно основная ) матрицы системы могут быть приведены к упрощенной форме.
Для того, чтобы решить систему уравнений , можно придерживаться следующей схемы:
Расширенную матрицу системы приводим к упрощенной форме.
Проверяем совместность, пользуясь теоремой Кронекера –Капелли.
Решаем упрощенную систему уравнений, если она оказалась совместной.
4.3 Метод Гаусса.
Поиск ранга матрицы удобно совместить с решением системы методом Гаусса, который обеспечивает последовательное исключение переменных и заключается в том , что с помощью элементарных преобразований СЛУ приводится к системе ступенчатого вида.
Если система имеет единственное решение, то ступенчатая система уравнений приводится к треугольной, т. е. к такой, в которой последнее уравнение содержит одно неизвестное. Переход системы к равносильной треугольной называют прямым ходом метода Гаусса, а нахождение переменных из треугольной системы- обратным ходом метода Гаусса.
В случае неопределенной системы, допускающей бесконечное множество решений , треугольной системы не получается.
Когда же система несовместна, то после приведения к ступенчатому виду она содержит хотя бы одно уравнение вида 0=1. Такая система не имеет решений.
ГЛАВА 5. ПРАКТИКУМ ПО НАХОЖДЕНИЮ РЕШЕНИЙ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ РАЗНЫМИ СПОСОБАМИ.
№ 1 Найти матрицу 3·А+4· B -5 ·E , если А=,В=,Е – единичная матрица.
Решение. Имеем 3·А=, 4· B =, 5 ·E =.
Решение. Имеем А=, 2·В Т =.
Произведение матриц 2·В Т и С возможно, т.к. в матрице 2·В Т один столбец, а в матрице С одна строка. Матрица 2·В Т ·С будет иметь размер 3×2.
Решение. Произведение матриц А и В возможно, т.к. в матрице А три столбца, а в матрице В три строки. Матрица A·B будет иметь размер 2×2.
Матрица произведение С 2 возможно, т.к. в матрице число столбцов равно числу строк. Матрица С 2 будет иметь размер 2×2.
Найдем D =( A·B ) T — C 2 =.
№ 4 Найти произведение матриц А·В, В·А, (А+В Т )·В, если А=,В=.
Решение. Произведение матриц А и В возможно, т.к. в матрице А три столбца, а в матрице В три строки. Матрица A·B будет иметь размер 2×2.
Произведение матриц В и А возможно, т.к. в матрице В два столбца, а в матрице А две строки. Матрица A·B будет иметь размер 2×3.
Произведение матриц А+В Т и В возможно, т.к. в матрице А+В Т три столбца, а в матрице В три строки. Матрица A·B будет иметь размер 2×2.
№ 5 Вычислить определитель .
Решение. Воспользуемся правилом треугольника:
№ 6 Вычислить определитель .
Решение. Вычислим определитель разложением по первой строке:
№ 7 Решить неравенство
Решение. Раскроем определитель:2(3х 2 -7)-12х 2 -14-12х 2 -12х-18
Решим это неравенство методом интервалов, получим х (-1;3).
№ 8 Решить уравнение =0.
Решение. Найдем определитель: (х-2)·(-1)·1+х·2·(-2)+3·2·3-(х·(-1)·3+2·3·1+(х-2)·(-2)·2), раскроем скобки:-х+2-4х+18+3х-6+4х-8=0, приведем подобные: 2х+6=0. Решим уравнение: х=-3.
№ 9 Решить систему линейных уравнений по формулам Крамера: .
Решение. ==5+21+12+10+6-21=33. Определитель данной системы отличен от нуля, следовательно, она имеет единственное решение. Находим его по формулам Крамера.
№ 10 Найти обратную матрицу для А=.
Решение. Определитель матрицы А=20.
Найдем алгебраические дополнения элементов матрицы А:
Матрица , обратная для матрицы А имеет вид:
№ 11 Найти обратную матрицу для А=.
Решение. Определитель матрицы А=10.
Найдем алгебраические дополнения элементов матрицы А:
Следовательно, А -1 =.
№ 12 С помощью элементарных преобразований вычислить ранг матрицы А=.
Решение. Прибавим к третьему столбцу второй, затем к первому столбцу прибавим удвоенный третий. Вычтем из второго столбца удвоенный третий
Ответ: ранг исходной матрицы равен 3.
№ 13 Решить систему линейных уравнений методом Гаусса, предварительно исследовав систему с помощью теоремы Кронекера-Капелли..
Решение. Выписав расширенную матрицу этой системы, после элементарных преобразований получим:
откуда rangA = rangB = n =3, следовательно, система совместна и является определенной. Значит система имеет единственное решение. Вернемся к системе уравнений:
Решение этой системы можно получить при использовании обратного хода метода Гаусса. Из последних двух уравнений можно найти y и z : y =11,5; z =10.Подставив их в первое уравнение, найдем х: x =36-10-11,5=14,5.
С помощью программы, которую я создала, найдем решение данной системы линейных уравнений . Вводим коэффициенты перед неизвестными в ABC Pascal
(Приложение таблица 1), получаем серии ответов:
№ 14 Решить систему линейных уравнений методом Гаусса, предварительно исследовав систему с помощью теоремы Кронекера-Капелли.
Решение: Выписав расширенную матрицу этой системы, после элементарных преобразований получим:
-4 7 5 -2 -4 7 5 -2 -4 7 5 -2
5 15 6 -9 0 — 0 0
-1 6 7 1 0 0 0 0 0
откуда rangA = rangB = n =3, следовательно, система совместна и является определенной. Значит система имеет единственное решение. Вернемся к системе уравнений:
Решение этой системы можно получить при использовании обратного хода метода Гаусса. Из последних двух уравнений можно найти х 2 и х 1.
Подставив нижнее выражение в верхнее, получим решение
Также решить данное уравнение можно с помощью составленной программы (Приложение таблица 1). Вводим коэффициенты перед неизвестными в ABC Pascal и получаем серии ответов:
№ 15 Исследовать систему линейных уравнений:
Приведем расширенную матрицу системы к ступенчатому виду:
Так как r ( A )= r ( A B )=2 4= n , то система совместна и определенна.
Количество главных переменных равно r (А)=2, количество свободных переменных равно n — r (А)=4-2=2.
№ 16 Исследовать систему линейных уравнений на наличие корней
Приведем к ступенчатому виду расширенную матрицу системы:
Так как r ( A )=2≠3= r ( B ), то система несовместна (не имеет решений). В самом деле, последней строке полученной расширенной матрицы соответствует уравнение 0·х 1 +0·х 2 +0х 3 =-13, не имеющее решение.
5.1ПРИМЕНЕНИЕ ЭЛЕМЕНТОВ ЛИНЕЙНОЙ АЛГЕБРЫ В ЭКОНОМИКЕ
Рассмотрим задачи, в которых необходимо использовать действия над матрицами или составлять и решать системы линейных алгебраических уравнений.
№ 1 Обувная фабрика специализируется по выпуску изделий трех видов: сапог, кроссовок и ботинок; при этом используется сырье трех типов: S 1 S 2 S 3 / нормы расхода каждого их них на одну пару обуви и объем расхода сырья на 1 день заданы таблицей:
Найти ежедневный объем выпуска каждого вида обуви.
Решение: Пусть ежедневно фабрика выпускает х 1 пар сапог, х 2 пар кроссовок и х 3 пар ботинок. Тогда в соответствии с расходом сырья каждого вида имеем систему:
Решая систему любым способом, находим(200,300,200), т.е. фабрика выпускает 200 пар сапог, 300-кроссовок и 200 пар ботинок.
№ 2 В три магазина завозят два раза в месяц одинаковое количество диванов, кресел, тумбочек. В первый – по 10 диванов, 6 кресел, 8 тумбочек, во второй –по 5 диванов, 7 кресел, 10 тумбочек, в третий – по 2 дивана, 3 кресла и 5 тумбочек. Во всех магазинах устанавливали одинаковые цены и меняли их в связи с завозами. Найдите суммарные месячные выручки, если в магазинах все распродали, и матрица цен выглядит так:
Реферат: Определители матрицы и системы линейных алгебраических уравнений
| Название: Определители матрицы и системы линейных алгебраических уравнений Раздел: Рефераты по математике Тип: реферат Добавлен 19:37:15 08 июня 2011 Похожие работы Просмотров: 7696 Комментариев: 23 Оценило: 8 человек Средний балл: 4.4 Оценка: 4 Скачать | |||
| Вложение | Размер |
|---|---|
| nou._reshenie_sistem_lineynykh_algebraicheskikh_uravneniy.doc | 515 КБ |
Предварительный просмотр:
Муниципальное бюджетное образовательное учреждение
Средняя общеобразовательная школа № 81
Сормовского района г. Н. Новгорода
Научное общество учащихся
«Решение систем линейных алгебраических уравнений»
Выполнил: Тихонов Никита,
ученик 10 «а» класса
Капочкина Антонина Николаевна,
1.Системы линейных алгебраических уравнений
2. Решение систем линейных алгебраических уравнений методом Крамера.
2.1. Основные понятия.
2.2 Определители второго порядка и их свойства.
2.3 Определители третьего порядка и их свойства.
2.4. Решение СЛАУ методом Крамера.
3. Матрицы и действия над ними.
3.2. Действия над матрицами.
3.3.Обратная матрица. Матричный метод решения СЛАУ.
4. Решение систем линейных алгебраических уравнений методом Гаусса.
4.1. Совместность СЛАУ.
4.2. Решение СЛАУ методом Гаусса.
Уравнения в школьном курсе алгебры занимают ведущее место. На их изучение отводится времени больше, чем на любую другую тему. Действительно, уравнения не только имеют важное теоретическое значение, но и служат чисто практическим целям. Подавляющее большинство задач о пространственных формах и количественных отношениях реального мира сводится к решению различных видов уравнений и их систем. Овладевая способами их решения, учащиеся находят ответы на различные вопросы из науки и техники (транспорт, сельское хозяйство, промышленность, связь и т.д.).
Многие теоритические и практические вопросы, приводят не к одному уравнению, а к целой системе уравнений с несколькими неизвестными.
Способы решения систем линейных уравнений – очень интересная и важная тема в школьном курсе математики, задания из данной темы были представлены на экзамене в 9 классе, а также входят в состав заданий для ЕГЭ.
С решением систем линейных уравнений мы познакомились в седьмом классе. Тогда мы решали системы линейных уравнений двумя способами:
- метод подстановки;
- метод сложения.
Нужно заметить, что не все методы решения системы линейных алгебраических уравнений рассматриваются в школьном курсе математики. Существуют и другие методы, например, такие, как: метод Крамера , Гаусса (исключение неизвестных), матричный способ.
С этими способами решения систем линейных уравнений мы познакомимся в данной исследовательской работе.
В процессе работы приобретаются навыки, с помощью которых последующее решение систем линейных уравнений станет намного проще и быстрее.
Рассмотреть решение систем линейных алгебраических уравнений методом Крамера, методом Гаусса и матричным методом.
- Познакомится с понятием определителя и методами его вычисления.
- Рассмотреть метод Крамера решения систем линейных алгебраических уравнений.
- Познакомиться с понятием матрицы, элементами матриц, и их элементарными преобразованиями.
- Рассмотреть решение систем линейных алгебраических уравнений матричным методом.
- Рассмотреть решение систем линейных алгебраических уравнений методом Гаусса.
1.Системы линейных алгебраических уравнений
1.1 Основные понятия и определения
Система m линейных уравнений с n переменными имеет вид:
где a ij, b i (i = 1,2,…,m; j = 1,2,…,n) – произвольные числа, называемые соответственно коэффициентами при переменных и свободными членами уравнений.
В более краткой записи с помощью знаков суммирования систему можно записать в виде:
Решением системы (1.1) называется такая совокупность n чисел ( x 1 = k 1, x 2 = k 2 ,…, x n = k n ), при подстановке которых каждое уравнение системы обращается в верное равенство.
Система уравнений называется совместной , если она имеет хотя бы одно решение, и несовместной , если она не имеет решений.
Совместная система уравнений называется определенной , если она имеет единственное решение, и неопределенной , если она имеет более одного решения. Например, система уравнений – совместная и определенная, так как имеет единственное решение (10;0); система – несовместная; а система уравнений – совместная и неопределенная, так как имеет более одного, а точнее бесконечное множество решений ( x 1 = c, x 2 = 20-c, где с – любое число).
Две системы уравнений называются равносильными , или эквивалентными , если они имеют одно и то же множество решений. С помощью элементарных преобразований системы уравнений получается система (1.1), равносильная данной.
2. Решение систем линейных алгебраических
уравнений методом Крамера.
2.1. Основные понятия.
Определителем n-го порядка называется число n , составленное по определенному правилу и записываемое в виде квадратной таблицы
Определитель вычисляется согласно указанному ниже правилу, по заданным числам ( ), которые называются элементами определителя (всего их n 2 ). Индекс i указывает номер строки, j – номер столбца квадратной таблицы (1), на пересечении которых находится элемент . Любую строку или столбец этой таблицы будем называть рядом.
Главной диагональю определителя называется совокупность элементов , , …, определителя (1).
Побочной диагональю определителя называется совокупность элементов , , …, определителя (1).
Минором M ij элемента a ij называется определитель (n–1)–го порядка n–1 , полученный из определителя n–го порядка n вычеркиванием i-й строки и jстолбца.
Алгебраическое дополнение A ij элемента a ij определяется равенством
A ij = (–1) i+j M ij (2)
Значение определителя n находится по следующему правилу.
Для n = 3 в определителе выбирается разрешающая строка или столбец, относительно которой или которого вычисляются определители 2-го порядка
Здесь в качестве разрешающей была выбрана первая строка определителя (4), однако, без ограничения общности, в качестве разрешающей может быть выбрана любая другая строка либо столбец.
В дальнейшем в качестве разрешающей будем рассматривать первую строку определителя.
Величины A 11 , A 12 , A 13 – алгебраические дополнения, а M 11 , M 12 , M 13 – миноры, соответствующие элементам a 11 , a 12 , a 13 определителя 3 . Эти миноры являются определителями второго порядка, получаемыми из определителя 3 вычеркиванием первой строки и соответствующих столбцов. Например, чтобы найти минор M 13 , следует в определителе 3 вычеркнуть первую строку и третий столбец, а из оставшихся элементов составить определитель второго порядка.
Для произвольного n
где A 1k = (–1) 1+k M 1k , а миноры M 1k , являющиеся определителями (n–1)-го порядка, получаются из n вычеркиванием первой строки и k-го столбца.
2.2 Определители второго порядка и их свойства.
Определителем второго порядка называется число
Приведем основные свойства определителей второго порядка.
- Величина определителя не изменится, если его строки поменять местами соответственными столбцами.
- При перестановке двух строк (столбцов) абсолютная величина определителя сохранится, а знак изменится на противоположный.
- Если определитель содержит две одинаковые строки (два одинаковых столбца), то его величина равна нулю.
- Общий множитель всех элементов строки (столбца) можно вынести за знак определителя.
- Если все элементы какой – либо строки (столбца) определителя равны нулю, то величина определителя равна нулю.
- Если к элементам какой – либо строки (столбца) определителя прибавить соответственные элементы другой строки (столбца), умноженные на одно то же число, то величина определителя не изменится.
Пример 1. Вычислить определитель ∆= .
Решение. По формуле (1) находим
Пример 2. Вычислить определитель ∆= .
Решение. Вынесем за знак определителя общие элементов 1-й и 2-й строк, т.е. числа 125 и 4:
Вынося за знак определителя общий множитель элементов 2-ого столбца, равный 4, получим
2.3 Определители третьего порядка и их свойства.
Определителем третьего порядка называется число
Свойства определителей третьего порядка аналогичны свойствам определителей второго порядка.
Пример 1. Вычислить определитель
Решение. По формуле (1) находим
Пример 2. Вычислить определитель
Решение. Вынося за знак определителя общие множители элементов 1, 2 и 3-й строк, получим
∆=3∙6∙2∙ =36∙ — 2 + 3 =36(4(1-5)-2∙0+3(5-
Пример 3. Вычислить определитель
Решение. Вынесем общий множитель элементов 2-й строки за знак определителя:
Вычтем из элементов 3-й строки соответственные элементы 1-й строки:
Так как определитель с двумя равными строками равен нулю, то ∆=7∙0=0.
Для вычисления определителя третьего порядка 3 часто пользуются привилом Сарруса (правило треугольников):
3 = a 11 a 22 a 33 + a 12 a 23 a 31 + a 21 a 32 a 13 – (a 13 a 22 a 31 + a 12 a 21 a 33 + a 23 a 32 a 11 )
Схематическая запись этого правила приведена ниже:
Пример 4. Вычислить определить 4-го порядка.
2.4. Решение СЛАУ методом Крамера.
Пусть задана система линейных алгебраических уравнений в следующем виде:
Пусть определитель матрицы A коэффициентов системы отличен от нуля, т.е. det A 0. Тогда справедливы формулы Крамера для вычисления неизвестных :
где , а являются определителями n-го порядка, которые получаются из путем замены в нем i-го столбца столбцом свободных членов исходной системы.
Пример 1. Решить систему уравнений с помощью формул Крамера:
= 56 – 18 + 20 + 21 = 79.
Последовательно заменяя в 3 первый, второй и третий столбцы столбцом свободных членов, получим
Пример 2. Решить систему уравнений
Найдем определитель системы =5. Так как то по теореме Крамера система имеет единственное решение.
Вычислим определители , , , полученных из матрицы А, заменой соответственно первого, второго и третьего столбцов столбцом свободных членов:
Теперь по формулам Крамера (1.8)
x 1 = ; x 2 = ; x 3 =
т. е. решение системы (4; 2; 1).
Пример 3. Решить систему уравнений
Система уравнений имеет одно решение, так как определитель отличен от нуля.
Остальные определители получим путем замены соответствующего столбца исходного определителя на столбец свободных членов системы уравнений.
Решения находим по формулам:
3. Матрицы и действия над ними.
Матрица размерами m × n – совокупность mn чисел, расположенных в виде прямоугольной таблицы из m строк и n столбцов, например (обозначим за А )
2 5 2
А = 3 10 7 — матрица. (1)
Числа, из которых состоит матрица, называются элементами матрицы. В общем виде матрицы:
а 11 a 12 … a 1n
a 21 a 22 … a 2n
M = a 31 a 32 … a 3n (2)
a m1 a m2 … a mn
они обозначаются буквами с двумя индексами: 1ый индекс указывает номер строки, а 2ой – номер столбца, в которых содержится этот элемент.
Если m = n, то матрица называется квадратной , а число строк (или столбцов) – её порядком .
Две матрицы, имеющие одинаковое количество строк и столбцов, называются матрицами одинакового типа. Две матрицы А = [a ij ] и В = [b ij ] одинакового типа называются равными , если a ij = b ij при всех i и j.
Матрица, состоящая из одной строки (одного столбца), называется матрицей-строкой ( матрицей-столбцом ), а матрица, у которой все элементы а ij = 0 , – нулевой или нуль матрицей.
Элементы квадратной матрицы, имеющие одинаковые значения индексов, составляют главную диагональ , а элементы квадратной матрицы порядка n ,сумма индексов каждого из которых равна n+1, – побочную диагональ.
Сумма элементов главной диагонали квадратной матрицы называется следом матрицы. Квадратные матрицы, у которых все элементы вне главной диагонали равны нулю, называются диагональными (обозначается Е ):
Квадратная матрица, все элементы которой, стоящие ниже (выше) главной диагонали, равны нулю, называется треугольной :
a 11 а 12 … а 1n b 11 0 … 0
А = 0 а 22 … а 2n ; B = b 21 b 22 … 0 (4)
0 0 … a nn b n1 b n2 … b nn
Диагональная матрица является частным случаем треугольной. Преобразование элементов квадратной матрицы, состоящее в замене строк соответствующими столбцами, называется транспонированием матрицы. Таким образом, если
a 11 a 12 … a 1n
A = a 21 a 22 … a 2n ; (5)
a n1 a n2 … a nn
то
a 11 a 21 … a n1
A T = a 12 a 22 … a n2 . (6)
a 1n a 2n … a nn
Определитель n-го порядка матрицы
а 11 а 12 … а 1n
А = а 21 а 22 … а 2n
а n1 а n2 … а nn
а 11 а 12 … а 1n
∆ = а 21 а 22 … а 2n = ∑ (-1) I(k , k , …, k ) a 1k a 2k … a nk (7)
а n1 а n2 … а nn
Здесь суммирование распространяется на всевозможные перестановки индексов элементов а ij , т.е. на всевозможные перестановки ( k 1 , k 2 , …, k n ). Числа а ij называют элементами определителя .
Квадратная матрица, определитель которой отличен от нуля, называется невырожденной, а матрица с определителем, равным нулю – вырожденной .
Определитель обладает некоторыми свойствами. Перечислим их:
- При транспонировании матрицы её определитель не изменяется.
2. Если все элементы некоторой строки определителя состоят из
нулей, определитель равен нулю.
3.От перестановки двух строк определитель меняет знак.
- Определитель, содержащий две одинаковые строки, равен нулю.
- Общий множитель всех элементов некоторой строки определителя можно вынести за знак определителя, или, если все элементы некоторой строки определителя умножить на одно и тоже число, то определитель умножается на это число.
- Определитель, содержащий две пропорциональные строки, равен нулю.
- Если все элементы i -й строки определителя представлены в виде суммы двух слагаемых, то определитель равен сумме двух определителей, у которых все строки, кроме i -й, те же, что и у данного определителя; i -я строка определителя состоит из первых слагаемых элементов i -й строки данного определителя, а i -я
строка другого – из вторых слагаемых элементов i -й строки.
- Определитель не изменяется, если к элементам одной строки прибавить соответствующие элементы другой строки, умноженные на одно и тоже число.
3.2. Действия над матрицами.
Основные операции, которые производятся над матрицами, – сложение, вычитание, умножение, а также умножение матрицы на число. Указанные операции являются основными операциями алгебры матриц – теории, играющей весьма важную роль в различных разделах математики и естествознания.
Суммой двух матриц А и В одинаковых размеров называется матрица того же размера, элементы которой равны сумме соответствующих элементов матриц А и В . Таким образом, если
а 11 … а 1n b 11 … b 1n
a m1 … а mn b m1 … b mn
a 11 + b 11 … a 1n + b 1n
a m1 + b m1 … a mn + b mn
Операция нахождения суммы матриц называется сложением матриц и распространяется на случай конечного числа матриц одинаковы размеров.
Так же, как и сумма, определяется разность двух матриц
a 11 – b 11 … a 1n – b 1n
A – B = ……………………… (10)
a m1 – b m1 … a mn – b mn
Операция нахождения разности двух матриц называется вычитанием матриц . Проверкой можно убедиться, что операция сложения матриц удовлетворяет следующим свойствам:
- А + В = В + А ; (коммутативность)
- А + (В + С) = (А + В) + С ; (ассоциативность)
- А + О = А .
Здесь А, В, С – произвольные матрицы одинаковых размеров; О – нулевая матрица того же размера.
Произведением матрицы А = [а ij ] на число λ называется матрица, элементы которой получаются из соответствующих элементов матрицы А умножением их на число λ. Произведение обозначим
λА. Таким образом от умножения матрицы (1) на число, получим:
a 11 … a 1n λa 11 … λa 1n
A = ………… , то λA = ……………… (11)
a m1 … a mn λa m1 … λa mn
Операция нахождения произведения матрицы на число называется умножением матрицы на число. Матрица –А = –1А называется противоположной матрице А . Проверкой можно убедиться, что операция умножения матрицы на число удовлетворяет следующим свойствам:
Здесь А, В – произвольные матрицы; μ, λ — произвольные числа; О – нулевая матрица.
Произведение АВ матрицы А на матрицу В определяется только в том случае, когда число столбцов матрицы А равно числу строк матрицы В . Пусть матрицы А и В такие, что число столбцов матрицы А равно числу строк матрицы В :
а 11 … а 1n b 11 … b 1n
a m1 … a mn b m1 … b mn
В этом случае произведением матрицы А на матрицу В , которые
заданы в определенном порядке ( А – 1ая, В – 2ая ), является матрица С , элемент которой с ij определяется по следующему правилу:
c ij = a i1 b 1j + a i2 b 2j + … + a in b nj = ∑ n α = 1 a iα b αj, (12)
где i = 1,2, …, m; j = 1, 2, …, k.
Для получения элемента с ij матрицы произведения С = АВ нужно элементы i -й строки матрицы А умножить на соответствующие элементы j -го столбца матрицы В и полученные произведения сложить. Например, если:
1 2 3 7 8
А = ; В = 9 10 , то (13)
4 5 6 11 12
1 7 + 2 9 + 3 11 1 8 + 2 10 + 3 12 58 64
АВ = = (14)
4 7 + 5 9 + 6 11 4 8 + 5 10 + 6 12 139 154
Число строк матрицы С = АВ равно числу строк матрицы А , а число столбцов – числу столбцов матрицы В .
Операция нахождения произведения двух матриц называется умножением матриц . Умножение матриц некоммутативно, т.е.
АВ ≠ ВА . Убедимся в примере матриц (13). Перемножив их в обратном порядке, получим:
39 54 69
ВА = 49 68 87 (15)
Сравнив правые части выражений (14) и (15), убедимся, что АВ ≠ ВА.
Матрицы А и В , для которых АВ = ВА, называются перестановочными . Например:
1 2 -3 2
А = ; В = перестановочны, т.к.
-2 0 -2 -4
-7 -6
Проверкой можно показать, что умножение матриц удовлетворяет следующим свойствам:
- А(ВС) = (АВ)С ; (ассоциативность)
- λ(АВ) = (λА)В = А(λВ);
- А(В + С) = АВ + АС . (дистрибутивность)
Здесь А, В, С – матрицы соответствующих определению умножения матриц размеров; λ — произвольное число.
Операция умножения двух прямоугольных матриц распространяется на случай, когда число столбцов в 1ом множителе равно числу строк во 2ом, в остальных случаях произведение не определяется. А также, если матрицы А и В – квадратные одного и того же порядка, то умножение матриц всегда выполнимо при любом порядке следования сомножителей.
3.3.Обратная матрица. Матричный метод решения СЛАУ.
Пусть дана квадратная матрица
a 11 … a 1n
A – её определитель.
Если существует матрица Х такая, что АХ = ХА = Е, где Е – единичная матрица, то матрица Х называется обратной по отношению к матрице А , а сама матрица А – обратимой . Обратная матрица для А обозначается А -1 .
Теорема 1.1. Для каждой обратимой матрицы существует только одна обратная ей матрица.
Д о к а з а т е л ь с т в о. Пусть для матрицы А наряду с матрицей Х существует еще хотя бы одна отличная от Х обратная матрица, которую обозначим за Х 1 . Тогда должны выполняться следующие условия: ХА = Е, АХ 1 = Е . Умножив второе равенство на матрицу Х , получим ХАХ 1 = ХЕ =Х. Но, т.к. ХА = Е , то предыдущее равенство можно записать в виде ЕХ 1 = Х или Х = Х 1 .
Т е о р е м а д о к а з а н а.
Пример 1. Найти матрицу обратную матрице
1 2 3
Р е ш е н и е. Проверим, обратима матрица А или нет, т.е. является ли она невырожденной:
1 2 3 1 2 5
∆ А = –3 –1 1 = –3 –1 0 = 5 –3 1 = 5 (–3 + 2) = –5 ≠ 0.
2 1 –1 2 1 0 2 1
Найдем алгебраические дополнения всех элементов матрицы А :
А 11 = –1 1 = 0; А 12 = – –3 1 = –1;
1 –1 2 –1
А 13 = –3 –1 = –1; А 21 = – 2 3 = 5;
2 1 1 –1
А 22 = 1 3 = –7; А 23 = – 1 2 = 3;
2 –1 2 1
А 31 = 2 3 = 5; А 32 = — 1 3 = –10;
А 33 = 1 2 = 5.
Составим присоединённую матрицу для матрицы А :
0 5 5
Отсюда находим обратную матрицу:
Пример 2. Найти неизвестную матрицу Х из уравнения АХ = В , если:
А = 2 3 ; В = 3 4 .
Р е ш е н и е. Умножив обе части данного матричного уравнения слева на матрицу А -1 , получим:
А -1 АХ = А -1 В; Х = А -1 В.
Найдем А -1 : ∆ А = 1, А 11 = 2, А 12 = -1, А 21 = -3, А 22 = 1 , следовательно,
Найдем матрицу Х:
Х = А -1 В = 2 -3 3 4 = 9 5 .
Пример1. Решите систему алгебраических линейных уравнений матричным методом.
А= 1 -1 4 ; Х= у ; В= -5
Найдём обратную матрицу А -1 :
∆ = 1 -1 4 = 4*(-1)*1 + 1*1*1 + 1*2*4 – 4*(-1)*1 – 1*1*4 – 1*
4 1 -4 *2*1 = -4+1+8+4-4-2=9-6=3 =0
Следовательно обратная матрица существует. Построим её:
Составим алгебраические дополнения к элементам матрицы А:
А 11 = (-1) 2 -1 2 = -6 А 12 = (-1) 3 1 2 =4 А 13 = (-1) 4 1 -1 = 5
А 21 = (-1) 3 1 1 = -3 А 22 = (-1) 4 1 1 =0 А 23 = (-1) 5 1 1 =3
А 31 = (-1) 4 1 1 =3 А 32 = (-1) 5 1 1 =-1 А 33 = (-1) 6 1 1 =-2
Составим матрицу из алгебраических дополнений:
Транспонируем полученную матрицу:
Умножим полученную матрицу на число, обратное определителю матрицы А т.е на 1/3:
А -1 = 4/3 0/3 -1/3 = 4/3 0 -1/3
5/3 3/3 -2/3 5/3 1 4/3
Х= 4/3 0 -1/3 * -5 = 4/3+2/3 = 2
5/3 1 4/3 -2 5/3-5+4/3 -2
Таким образом, х=1,у= 2, z= -2
Ответ: х=1,у= 2, z= -2
Найдем алгебраические дополнения
Отсюда получаем x = 2, y = 3, z =1.
4 . Решение систем линейных алгебраических
уравнений методом Гаусса.
4.1. Совместность СЛАУ.
Одним из ключевых понятий при решении систем линейных алгебраических уравнений является понятие ранга матрицы. Введем это понятие. Выделим в матрице A размерности m n k строк и k столбцов, где k – число, меньшее или равное меньшему из чисел m и n. Определитель порядка k, составленный из элементов, стоящих на пересечении выделенных k строк и k столбцов, называется минором или определителем , порожденным матрицей A. Например, для матрицы
при k = 2 определители
будут порожденными данной матрицей.
Рангом матрицы A (обозначается rang A) называется наибольший порядок порожденных ею определителей, отличных от нуля. Если равны нулю все определители порядка k, порожденные данной матрицей, то rang A
Теорема 1. Ранг матрицы не изменится, если
- Поменять местами любые два параллельных ряда.
- Умножить каждый элемент ряда на один и тот же множитель 0.
- Прибавить к элементам ряда соответствующие элементы другого параллельного ряда, умноженные на один и тот же множитель.
Преобразования 1–3 называются элементарными . Две матрицы называются эквивалентными, если одна матрица получается из другой с помощью элементарных преобразований.
Базисным минором матрицы называется всякий отличный от нуля минор, порядок которого равен рангу данной матрицы.
Минор M k+1 порядка k+1, содержащий в себе минор M k порядка k, называется окаймляющим минором M k . Если у матрицы A существует минор M k 0, а все окаймляющие его миноры M k+1 = 0, то rang A = k.
Пример. Найти ранг матрицы
Имеем . Для M 2 окаймляющими будут только два минора:
каждый из которых равен нулю. Поэтому rang A = 2, а указанный минор M 2 может быть принят за базисный.
Теорема 2 (Кронекера-Капелли). Для того, чтобы система m линейных алгебраических уравнений относительно n неизвестных x 1 , x 2 , …, x n
была совместна (имела решение), необходимо и достаточно, чтобы ранг основной матрицы
системы и ранг так называемой расширенной матрицы
системы были равны, т.е. rang A = rang B = r.
Далее, если rang A = rang B и r = n, то система имеет единственное решение; если r
Система называется однородной, если все ее свободные члены b i (i = 1, m) равны нулю. Если хотя бы одно из чисел отлично от нуля, то система называется неоднородной. Для однородной системы уравнений rang A = rang B, поэтому она всегда совместна.
4.2. Решение СЛАУ методом Гаусса.
Метод Гаусса – метод последовательного исключения переменных – заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которой последовательно, начиная с последних (по номеру) переменных, находится все остальные переменные.
Пусть задана система линейных алгебраических уравнений в следующем виде:
(1)
Пусть все хотя бы один из свободных членов системы уравнений отличен от нуля, т.е. система неоднородна. Если основная матрица A системы имеет ранг r = n, то расширенная матрица B этой системы с помощью элементарных преобразований строк и перестановок столбцов всегда может быть приведена к треугольному виду, где на главной диагонали матрицы располагаются единицы, а все элементы ниже главной диагонали равны нулю:
Эта матрица является расширенной матрицей системы
которая эквивалентна исходной системе (т.е. имеет те же самые решения, что и исходная система). Если хотя бы одно из чисел отлично от нуля, то система (2) и исходная система (1) несовместны. Если же , то система (1) совместна, а из системы (2) можно последовательно выразить в явном виде базисные переменные через свободные переменные . Если r = n, то решение этой системы единственно. В дальнейшем будем рассматривать последний случай, т.е. когда r = n.
Пример 1. Решить систему уравнений:
Р е ш е н и е. Расширенная матрица системы имеет вид:
Шаг 1. Так как a 0, то умножая вторую, третью и четвертую строки матрицы на числа (-2), (-3), (-2) и прибавляя полученные соответственно ко второй, третьей, четвертой строкам, исключим переменную x 1 из всех строк, начиная со второй. Поменяем местами вторую и третью строки:
Шаг 2. Умножая вторую строку на (-7/4) и прибавляя полученную строку к четвертой, исключим переменную x 2 из всех строк, начиная с третьей:
Шаг 3. Умножаем третью строку на 13,5/8=27/16, и прибавляя строку к четвертой, исключим из нее переменную x 3 . Получим систему уравнений
откуда, используя обратный ход метода Гаусса, найдем из четвертого уравнения x 4 =-2; из третьего x 3 = = =-1; из второго x 2 = = =2 и из первого уравнения x 1 =6+2 x 4 -3 x 3 — -2 x 2 =6+2(-2)-3(-1)-2·2=1, т.е. решение системы (1; 2; -1; 2).
Пример 2. Методом Гаусса решить систему уравнений:
Р е ш е н и е. Преобразуем расширенную матрицу системы
Итак, уравнение, соответствующее третьей строке последней матрицы, противоречиво – оно привелось к неверному равенству 0=-1, следовательно, данная система несовместна.
Пример3. С помощью метода последовательных исключений Гаусса решить вопрос о совместности данной системы и в случае совместности решить ее.
Составим расширенную матрицу B и проведем необходиые элементарные преобразования строк:
Последней матрице соответствует система, эквивалентная исходной
Из нее, двигаясь снизу вверх, последовательно находим: x 4 = –1, x 3 = 1, x 2 = 0, x 1 = –2.
Пример 4. . Методом Гаусса решить систему уравнений:
Запишем расширенную матрицу коэффициентов системы уравнений
Произведем элементарные преобразования со строками расширенной матрицы.
Разделим все элементы первой строки расширенной матрицы на 2.
Вычтем из второй строки первую, умноженную на 3.
Вычтем из третьей строки первую, умноженную на 1.
Теперь умножим все элементы второй строки расширенной матрицы на -2/11.
Вычтем из третьей строки вторую, умноженную на ½.
Теперь умножим все элементы третьей строки расширенной матрицы на -11/16
Произведенные выше элементарные преобразования – это прямой ход в метода Гаусса
Теперь нужно провести алгебраические преобразования в обратном порядке:
сначала с элементами третьего столбца, а затем второго столбца расширенной матрицы
Вычтем из второй строки третью, умноженную на (-1/11), а из первой строки третью, умноженную на 1/2
Вычтем из первой строки вторую, умноженную на 3/2
В результате последнего преобразования было получено решение системы уравнений:
Работа над это темой была очень интересной.
− в процессе работы я узнал много нового;
− я научился пользоваться научной литературой, сопоставлять и сравнивать различные точки зрения, выделять главное;
− теперь я знаю, какие действия можно выполнять над матрицами, какой путь решения систем линейных уравнений наиболее простой и быстрый, и ещё в своей работе я изучила многие другие теоретические вопросы;
− также весь материал я исследовал не только теоретически, но и практически, приводя некоторые примеры в тексте.
Тема решения систем линейных уравнений предлагается на выпускных экзаменах, поэтому умение их решать очень важно.
Исследовательская работа может использоваться учащимися, как пособие для самостоятельного изучения по теме „Методы решения систем линейных уравнений ”, а также в качестве дополнительного материала.
- Кремер Н. Ш. Высшая математика для экономистов: Учебное пособие для ВУЗов.- М.: Издательское объединение «ЮНИТИ», 1997.
- Апанасов П. Т., Орлов М. И. Сборник задач по математике: Учебное пособие для техникумов. — М.: Высшая школа, 1987.
- Демин И. И. Математика для экономистов: Программа курса и практические задания. – М.: МИЭП, 1997.
- Большой энциклопедический словарь «Математика». Ю.В.Прохоров 2000 г.
- Справочник по математике для средних учебных заведений. А.Г.Цыпкин Москва «Наука» 1983г.
http://www.bestreferat.ru/referat-218196.html
http://nsportal.ru/ap/library/drugoe/2014/06/26/reshenie-sistem-lineynykh-algebraicheskikh-uravneniy-10-klass


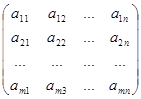
 = E,
= E, — симметрическая матрица
— симметрическая матрица называется диагональной матрицей.
называется диагональной матрицей. cij = aij ± bij
cij = aij ± bij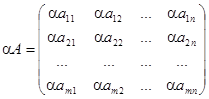
 ; B =
; B =  , найти 2А + В.
, найти 2А + В. , 2А + В =
, 2А + В =  .
.
 .
. ; В = А Т =
; В = А Т = ;
; , В =
, В =  , С =
, С =  и число a = 2. Найти А Т В+aС.
и число a = 2. Найти А Т В+aС. ; A T B =
; A T B =  =
=  ;
; ; А Т В+aС =
; А Т В+aС =  .
. и В =
и В =  .
. .
. , В =
, В = 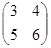
 =
=  .
. называется число, которое может быть вычислено по элементам матрицы по формуле:
называется число, которое может быть вычислено по элементам матрицы по формуле: det A =
det A =  , где
, где det A =
det A = 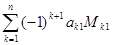
 detA =
detA =  , i = 1,2,…,n.
, i = 1,2,…,n.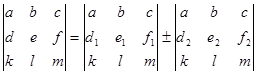
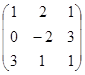
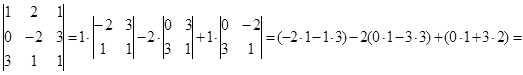
 , В =
, В =  . Найти det (AB).
. Найти det (AB). , det (AB) = 7×18 — 8×19 = 126 – 152 = -26.
, det (AB) = 7×18 — 8×19 = 126 – 152 = -26. , i=(1,n), j=(1,n),
, i=(1,n), j=(1,n), ,
, , найти А -1 .
, найти А -1 .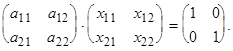
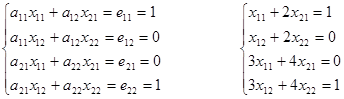
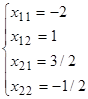
 .
.
 ,
,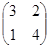 , найти А 3 .
, найти А 3 . ; A 3 =
; A 3 =  .
. .
.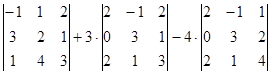
 = -1(6 – 4) – 1(9 – 1) + 2(12 – 2) = -2 – 8 + 20 = 10.
= -1(6 – 4) – 1(9 – 1) + 2(12 – 2) = -2 – 8 + 20 = 10. =
=  = 2(0 – 2) – 1(0 – 6) = 2.
= 2(0 – 2) – 1(0 – 6) = 2. =
=  = 2(-4) – 3(-6) = -8 + 18 = 10.
= 2(-4) – 3(-6) = -8 + 18 = 10.

 ,
,  RgA = 2.
RgA = 2.


 ,
,  Rg = 2.
Rg = 2.
 ,
,  Þ Rg = 2.
Þ Rg = 2.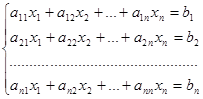
 ; X =
; X =  .
.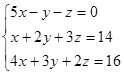
 , B =
, B =  , A =
, A = 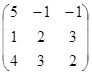
 5(4-9) + 1(2 – 12) – 1(3 – 8) = -25 – 10 +5 = -30.
5(4-9) + 1(2 – 12) – 1(3 – 8) = -25 – 10 +5 = -30. = -5; M21 =
= -5; M21 =  = 1; M31 =
= 1; M31 =  = -1;
= -1; M22 =
M22 =  M32 =
M32 = 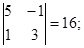
 M23 =
M23 =  M33 =
M33 = 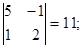
 A -1 =
A -1 =  ;
; =E.
=E. = А -1 В =
= А -1 В =  =
=  .
.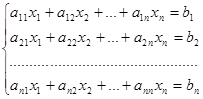
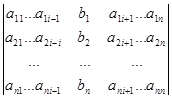
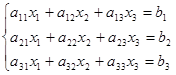
 ; D1 =
; D1 =  ; D2 =
; D2 =  ; D3 =
; D3 =  ;
;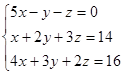
 = 5(4 – 9) + (2 – 12) – (3 – 8) = -25 – 10 + 5 = -30;
= 5(4 – 9) + (2 – 12) – (3 – 8) = -25 – 10 + 5 = -30; = (28 – 48) – (42 – 32) = -20 – 10 = -30.
= (28 – 48) – (42 – 32) = -20 – 10 = -30. = 5(28 – 48) – (16 – 56) = -100 + 40 = -60.
= 5(28 – 48) – (16 – 56) = -100 + 40 = -60. = 5(32 – 42) + (16 – 56) = -50 – 40 = -90.
= 5(32 – 42) + (16 – 56) = -50 – 40 = -90. ; Ответ: x = 0; y = 0; z = -2.
; Ответ: x = 0; y = 0; z = -2.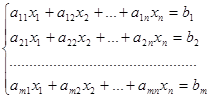 ,
, называется матрицей системы, а матрица
называется матрицей системы, а матрица называется расширенной матрицей системы
называется расширенной матрицей системы + x2
+ x2  + … + xn
+ … + xn 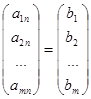
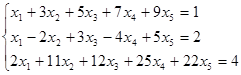
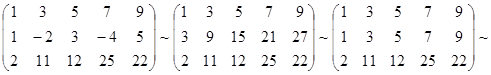
 .
.  RgA = 2.
RgA = 2. RgA* = 3.
RgA* = 3. А =
А =  ;
;  = 2 + 12 = 14 ¹ 0; RgA = 2;
= 2 + 12 = 14 ¹ 0; RgA = 2;
 RgA* = 2.
RgA* = 2. , где d1j = a1j /a11 , j = 2, 3, …, n+1.
, где d1j = a1j /a11 , j = 2, 3, …, n+1.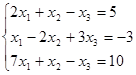
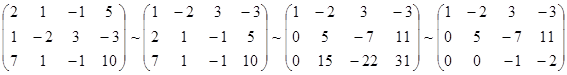
 , откуда получаем: x3 = 2; x2 = 5; x1 = 1.
, откуда получаем: x3 = 2; x2 = 5; x1 = 1.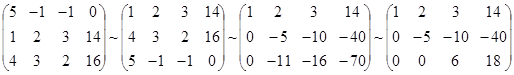
 , откуда получаем: z = 3; y = 2; x = 1.
, откуда получаем: z = 3; y = 2; x = 1.