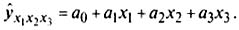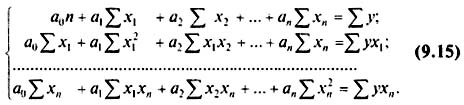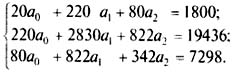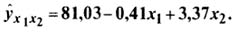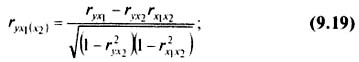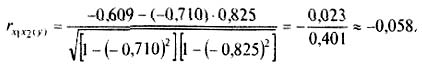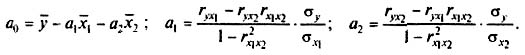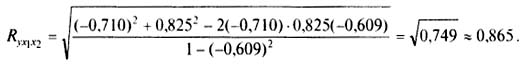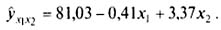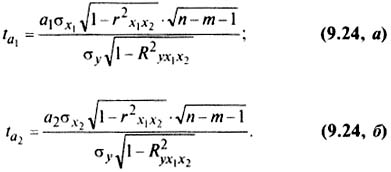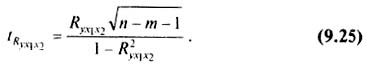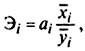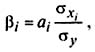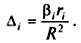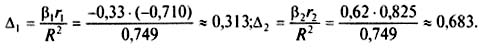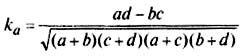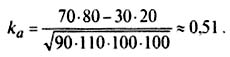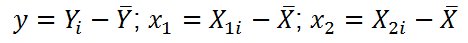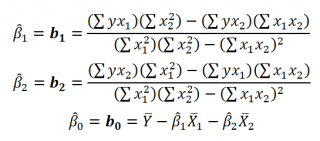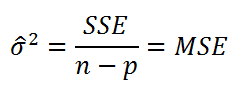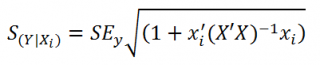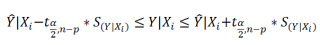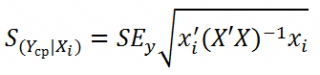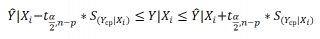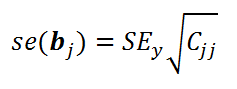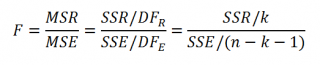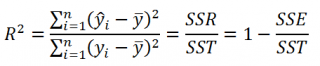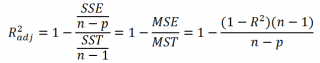Контрольная работа: Построение двухфакторной модели, моделей парной линейной прогрессии и множественной линейной регрессии
| Название: Построение двухфакторной модели, моделей парной линейной прогрессии и множественной линейной регрессии Раздел: Рефераты по экономико-математическому моделированию Тип: контрольная работа Добавлен 06:38:33 25 марта 2010 Похожие работы Просмотров: 1383 Комментариев: 22 Оценило: 4 человек Средний балл: 5 Оценка: неизвестно Скачать | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| n | у | х1 | х2 | х3 |
| 1 | 88 | 38 | 54 | 87 |
| 2 | 71 | 49 | 92 | 57 |
| 3 | 62 | 44 | 74 | 68 |
| 4 | 49 | 78 | 76 | 42 |
| 5 | 76 | 62 | 41 | 76 |
Для получения искомых величин составим расчетную таблицу:
Получим: x1 = 54,2, х2=67,4, х3= 66; у*х1=3617; у*х2=4542,4; у*х3=4750,6; х1*х2=3657,2; х1*х3=3415,8; х2*х3= 4256,4
Рассчитаем r коэффициент корреляции между величинами у и х1; у и х2; у и х3; х1 и х2; х2 и х3; х1 и х3;
Rх1х2 = cov(х1;х2)=4,12= 4,12 = 0,016
Построим расчетную таблицу для двухфакторной модели
Для построения двухфакторной модели по модулю подходят х1 и х3 т.к у них более высокий показатель, но по факторному признаку х1 и х3> 0,6 значит выбираем х1 и х2
Результаты обследования десяти статистически однородных филиалов фирмы в таблице (цифры условные). Требуется:
А. Построить модель парной линейной прогрессии производительности труда от фактора фондовооруженности, определить коэффициент регрессии, рассчитать парный коэффициент корреляции, оценить тесноту корреляционной связи, найти коэффициент эластичности и бета – коэффициент: пояснить экономический смысл всех коэффициентов;
Б. Построить модель множественной линейной регрессии производительности труда от факторов фондо- и энерго- вооруженности, найти все коэффициенты корреляции и детерминации, коэффициенты эластичности и — коэффициенты, пояснить экономический смысл всех коэффициентов.
А. Обозначим производительность труда через у – резтивный признак, два других признака фондовооруженость и энерговооруженность будут фак.х1 и х2. Рассмотрим линейную модель зависимости производительности труда – у от величины фондовооруженности – х 1 это модель выражения линейной функции f вида у = а0 + а1*х1, параметры которой находят в результате решения системы нормального уровня, сформированных на основе метода наименьших квадратов, суть которого заключается в то, что бы сумма квадратов отклонений фактических уравнений ряда от соответствующих, выровненных по кривой роста значений была наименьшей.

где суммирование приводится по всем
— параметры а 0 и а 1можно рассчитать по формуле:


396*а 0+15838*а 1 = 38856
Составим расчетную таблицу
Из расчета таблицы имеем
ух 1 = 95,9*39,6 = 3797,64
х 1 = (39,6)^2 = 1568.16
а 1 = 3885,6-3797,64 = 87,96 = 5,624040
а 0 = 95,9-5,624040*39,6 = -126,81,
таким образом однофакторная модель имеет вид:
у регр = -126,812+5624041*х 1
Полученное уравнение является уравнением парной регрессии, коэффициента а 1 в этом уравнении называется коэффициентом регрессии. Знак этого коэффициента определяется направлением связи между у и х 2. В нашем случае эта связь образуется а 1 = +5,624040(+) – связь прямая.

rух1 = V1-о у регр.^ 2/ оу^2 , где оу – средняя квадратная ошибка выборки у из значений таблицы
| rух1 | 0.8809071 |
rух1 = V1-142.79937/637.49 = 0.8809071
Чем ближе коэффициент корреляции к единице, тем теснее корреляционная связь: rух1=0,881, следовательно, связь между производительностью труда и фондовооруженностью достаточно тесная.
Коэффициент детерминации rух1^2
| rух1^2 | 0.7759974 |
Это означает, что фактором фондовооруженности можно объяснить 77,6% изменения производительности труда.
Коэффициент эластичности Эух1 = а1*х1 ср./ у ср.; Эух1 = 5,624040*39,6/95,9
| Эух1 | 2,322336 |
Это означает, что при увеличении фондовооруженности на 1%, производительность труда увеличится на 2,3223%.
Бета коэффициент _ух1 = а1*ох1/оу,
_ух1 = 5,624040*V15.64/ V637,49 = 0,8809072
| _ух1 | 0,8809072 |
Это значит, что увеличение фондовооруженности на величину среднеквадратического отклонения этого показателя приведет к увеличению среднего значения производительности труда на 0,88 среднеквадратического отклонения.
Б. Модуль множественных регрессий рассматривается на периметре двухфакторной линейной модели, отражающей зависимость производительности труда у, от величины фондовооруженности (х 1) и энерговооруженности (х 2), модуль множественной регрессии имеет вид у = а 0+а 1у 1+а 2х 2.Параметры модели а 0,а 1,а 2, находятся путем решения системы нормальных уравнений:


396*а 0+15838*а 1+31689*а 2 = 38859
787*а 0+31689*а 1+64005*а 2 = 78094
Решаем систему нормальным уравнением,методом Гаусса (метод исключения неизвестных).
Разделим каждое уравнение системы на коэффициент при а 0 соответственно:

а 0+39,994949*а 1+80,022727*а 2 = 98,128787
а 0+40,26556*а 1+81,327827*а 2 = 99,229987
из первогоуравнения системы вычитаем второе уравнение системы

а 0 +39,994949а 1+30,022727а 2 = 98,128787
Из первого вычитаем третье уравнение:

а 0+40,26556*а 1+81,327827*а 2 = 99,229987
получим систему с двумя неизвестными

0,665565*а 1+2,627827а 2 = 3,329987
Делим каждое уравнение на β при а 1 соответственно:

а 1+3,948265а 2 = 5,003248
из первого вычитаем второе
| а 2 = -1,0681323 |
Полученное значение а 2 подставим в уравнение с двумя неизвестными:
а 1+3,349108а 2 = 5,643227
а 1 = 5,643227-3,349108*(-1,0681323)
а 1 = 5,643227+3,577290
| а 1 =9,220517 |
Полученное значение а 1 и а 2 подставим в любое из уравнений с тремя неизвестными
а 0 = 95,9-39,6*9,220517-78,7*(-1,0681323)
а 0 = 95,9-365,132473+84,062012
| а 0 = -185,170461 |
у = -185,170461+9,220517х 1-1,0681323х 2
Ответ: у = -185,170461+9,220517х 1-1,0681323х 2
Парные коэффициенты корреляции:
| rух 1 | 0,881 |
| rух 2 | 0,722 |
| ох 2 | 14,38 |
| rх 1х 2 | 0,921 |
Чем ближе коэффициент корреляции к 1, тем теснее связь.
Коэффициент множественной корреляции:
| rх 1х 2 | 0,91 |
Таким образом, степень тесноты связи производительности труда с факторами фондовооруженности и энерговооруженности является высокой.
Совокупный коэффициент детерминации:
Это означает, что совместное влияние двух факторов определяет 82,9% производительности труда.
Частные коэффициенты корреляции:
| r ух 1(х 2) | 0,831 |
т.е. теснота связи между производительностью труда и фондовооруженностью, при энерговооруженности, значительная.
| rух 2(х 1) | -0,486 |
т.е. связи между производительностью труда и энерговооруженностью, при неизменной фондовооруженности, в данной выборке нет.
Частные коэффициенты эластичности:
| эух 1(х 2) | 3.807 |
т.е. при увеличении фондовооруженности на 1% и неизменной энерговооруженности, производительность труда увеличится на 3,807%.
| эух 2(х 1) | -0,877 |
т.е. при увеличении энерговооруженности, производительность труда не изменится.
Частные бета β коэффициенты:
| βух 1(х 2) | 1,444 |
это означает, что при неизменной энерговооруженности, увеличение на величину среднеквадратического отклонения размера фондовооруженности приведет к увеличению средней производительности труда на 1,444 среднеквадратического отклонения.
Решение. 3 страница
Анализируя остатки, можно сделать ряд практических выводов. Значения остатков (см. табл.9.2) имеют как положительные, так и отрицательные отклонения от ожидаемого уровня анализируемого показателя. Экономический интерес представляют выработки рабочих, обозначенных номерами: 5: 1; 4: 8; 7, поскольку их выработки отличаются наибольшими отклонениями. Тем самым выявляются передовые рабочие — номера: 1: 8; 7, обеспечивающие наибольшее повышение средней выработки (наибольшие положительные остатки) и отстающие, требующие особого внимания рабочие — номера: 5, 4 (наибольшие отрицательные остатки). В итоге положительные отклонения выработки большинства рабочих уравновешиваются отрицательными отклонениями небольшого числа рабочих, т.е. ∑ εi = 0.
9.2.2.6. Построение и статистический анализ двухфакторной линейной модели (трехмерной регрессии)
Для расчета параметров простейшего уравнения множественной линейной двухфакторной регрессии
где ŷx1x2 — расчетные значения зависимой неременной (результативного признака):
x1x2 — независимые переменные (факторные признаки);
Построим следующую систему нормальных уравнений:
Параметры этой системы могут быть найдены, например, методом К. Гаусса.
9.2.2.7. Трехфакторные линейные регрессионные модели
В случае линейной трехфакторной связи уравнение регрессии имеет вид
Для расчета параметров по способу наименьших квадратов используют следующую систему нормальных уравнений:
Чтобы получить эту систему, необходимо иметь таблицу значений следующих показателей:
Для решения множественной регрессии с n -факторами 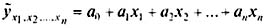
Вручную целесообразно выполнять построение и анализ только двух-, максимум трехфакторных моделей. Для п >3 все расчеты рекомендуется осуществлять на компьютерах по специальным программам, предусматривающим исчисление параметров уравнения и показателей, используемых для проверки его адекватности.
Многофакторный корреляционный и регрессионный анализ может быть использован в экономико-статистических исследованиях:
- для приближенной оценки фактического и заданного уровней;
- в качестве укрупненного норматива (для этого достаточно в уравнение регрессии подставить вместо фактических значений факторов их средние значения);
- для выявления резервов производства;
- для проведения межзаводского сравнительного анализа и выявления на его основе скрытых возможностей предприятий;
- для краткосрочного прогнозирования развития производства и др.
Построение и анализ трехмерной регрессионной модели рассмотрим на конкретном примере.
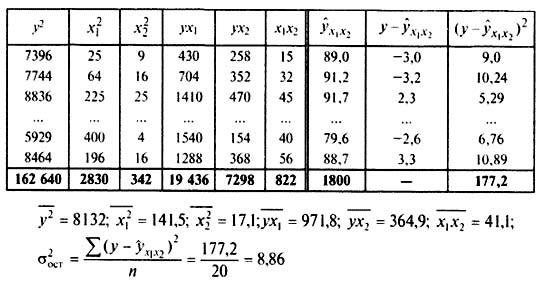
Пример 2. По выборочным данным, представленным в табл.9.3, о выработке деталей за смену 20 рабочими цеха требуется выявить зависимость производительности труда у от двух факторов: внутрисменных простоев x1 и квалификации рабочих x2.
Стохастическая связь между производительностью труда, внутрисменными простоями и квалификацией рабочих
Теоретический анализ исходных данных позволяет установить наличие причинно-следственной связи факторных признаков (внутри-сменных простоев и квалификации рабочих) с результативным показателем — производительностью труда. Регрессионную двухфакторную модель построим в линейной форме 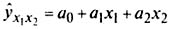
Для нахождения параметров этого уравнения произведем вычисления вспомогательных величин, которые запишем в табл. 9.4.
К расчету параметров и оценке линейной двухфакторной регрессионной модели
Составим систему нормальных уравнений:
Решая данную систему методом К. Гаусса, получаем
Уравнение множественной регрессии, выражающее зависимость производительности труда ŷ от внутренних простоев x1 и квалификации рабочих x2, примет вид:
Вычислим по нему ŷx1 x1 и занесем полученные значения в табл.9.4.
После построения регрессионной модели необходимо исчислить различного рода характеристики тесноты связи между
зависимой и независимой переменными: парные, частные и множественные коэффициенты корреляции, множественный коэффициент детерминации, а затем проверить адекватность данной модели.
9.2.2.8. Парные коэффициенты корреляции
Для измерения тесноты связи между двумя из рассматриваемых переменных (без учета их взаимодействия с другими переменными) применяются парные коэффициенты корреляции. Методика расчета таких коэффициентов и их интерпретация аналогичны методике расчета линейного коэффициента корреляции в случае однофакторной связи. Если известны средние квадратические отклонения анализируемых величин, то парные коэффициенты корреляции можно рассчитать проще по следующим формулам:
Предварительно исчислим средние квадратические отклонения:
Тогда парные коэффициенты корреляции будут равны:
9.2.2.9.Частные коэффициенты корреляции
Однако в реальных условиях все переменные, как правило, взаимосвязаны. Теснота этой связи определяется
частными коэффициентами корреляции, которые характеризуют степень и влияние одного из аргументов на функцию при условии, что остальные независимые переменные закреплены на постоянном уровне. В зависимости от количества переменных, влияние которых исключается, частные коэффициенты корреляции могут быть различного порядка: при исключении влияния одной переменной получаем частный коэффициент корреляции первого порядка; при исключении влияния двух переменных — второго порядка и т.д. Парный коэффициент корреляции между функцией и аргументом обычно не равен соответствующему частному коэффициенту.
Частный коэффициент корреляции первого порядка между признаками x1 и у при исключении влияния признака x2 вычисляют по формуле:
то же — зависимость у от x2 при исключении влияния x1:
Можно рассчитать взаимосвязь факторных признаков при устранении влияния результативного признака:
где r — парные коэффициенты корреляции между соответствующими признаками.
Выполним расчет частных коэффициентов корреляции для нашею примера:
Итак, связь каждого фактора с изучаемым показателем при условии комплексного воздействия факторов слабее. Практически отсутствует связь между факторными признаками при элиминировании результативного показателя rx1x2(y) = -0,058. Это вполне понятно — внутрисменные простои и квалификация рабочих никак не связаны между собой (если не принимать во внимание необходимость выполнения задания). Другое дело, если стоит вопрос о выполнении задания: более квалифицированный рабочий допустит меньше внутрисменных простоев. Значение парного коэффициента корреляции, в этом случае rx1x2 = -0,609 , подтверждает наличие довольно заметной обратной связи между этими факторами.
Изучение парных и частных коэффициентов корреляции позволяет отобрать наиболее существенные, значимые факторы.
На основе парных коэффициентов корреляции и средних квадратических отклонений можно легко рассчитать параметры уравнения линейной двухфакторной связи 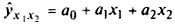
9.2.2.11. Совокупный коэффициент множественной детерминации
Совокупным коэффициентом множественной детерминации. называется величина R 2 , которая показывает, какая доля вариации изучаемого показателя объясняется влиянием факторов, включенных в уравнение множественной регрессии. Значение совокупного коэффициента множественной детерминации находится в пределах от 0 до 1. Поэтому, чем ближе R 2 к единице, тем вариация изучаемого показателя в большей мере характеризуется влиянием отобранных факторов.
Для выявления, в нашем примере, тесноты связи производительности труда с обоими факторами одновременно исчисляем совокупный коэффициент множественной корреляции:
Совокупный коэффициент множественной детерминации R 2 yx1x2 = 0,749 показывает, что вариация производительности труда на 74,9% обусловливается двумя анализируемыми факторами. Значит, выбранные факторы существенно влияют на показатель производительности труда. Таким образом, изучаемая с помощью многофакторного корреляционного и регрессионного анализа стохастическая связь между исследуемыми показателями свидетельствует о целесообразности построения двухфакторной регрессионной модели производительности труда в виде линейного уравнения регрессии:
9.2.2.12. Многошаговый регрессионный анализ
Однако показатели множественной регрессии и корреляции могут оказаться подверженными действию случайных факторов. Поэтому только после проверки адекватности уравнения оно
может быть пригодно, например, для выявления резервов повышения производительности труда.
Общая оценка адекватности уравнения может быть получена с помощью дисперсионного F-критерия Фишера. Применение же в этих целях множественного коэффициента корреляции недопустимо ввиду того, что многофакторный регрессионный анализ оперирует случайными наблюдениями, но не обязательно распределенными по многомерному нормальному закону (этому закону должны подчиняться отклонения фактических значений функции от расчетных). Совокупный коэффициент множественной детерминации определяет только качество выравнивания по уравнению регрессии.
Проверку значимости уравнения регрессии производят на основе вычисления F-критерия Фишера:
где m — число параметров в уравнении регресси.
Полученное значение — критерия Fрасч сравнивают с критическим (табличным) для принятого уровня значимости 0,05 или 0,01 и чисел степеней свободы v1 = m — 1 и v2 = n — m. Если оно окажется больше соответствующего табличного значения, то данное уравнение регрессии статистически значимо, т. е. доля вариации, обусловленная регрессией, намного превышает случайную ошибку.
Принято считать, что уравнение регрессии пригодно для практического использования в том случае, если Fрасч > Fтабл не менее чем в 4 раза.
Для оценки значи.чости коэффициентов регрессии при линейной зависимости y от x1 и x2— (двух факторов) используют t — критерий Стьюдента при n — m — 1 степенях свободы:
Существенность совокупного коэффициента корреляции определяют по формуле:
Если в уравнении все коэффициенты регрессии значимы, то данное уравнение признают окончательным и применяют в качестве модели изучаемого показателя для последующего анализа.
Оценку значимости коэффициентов регрессии с помощью t-критерия используют для завершения отбора существенных факторов в процессе многошагового регрессионного анализа. Он заключается в том, что после оценки значимости всех коэффициентов регрессии из модели исключают тот фактор, коэффициент при котором незначим и имеет наименьшее значение критерия. Затем уравнение регрессии строится без исключенного фактора, и снова проводится оценка адекватности уравнения и значимости коэффициентов регрессии. Такой процесс длится до тех пор, пока все коэффициенты регрессии не окажутся значимыми, что свидетельствует о наличии в регрессионной модели только существенных факторов. В некоторых случаях расчетное значение tрасч находится вблизи tтабл. поэтому с точки зрения содержательности модели такой фактор можно оставить для последующей проверки его значимости в сочетании с другим набором факторов.
Последовательный отсев несущественных факторов рассмотренным выше приемом (или последовательным включением новых факторов) составляет основу многошагового регрессионного анализа.
Проверим адекватность построенной двухфакторной модели производительности труда по F-критерию Фишера:
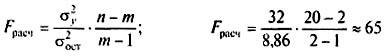
9.2.2.13. Экономическая интерпретация многофакторной регрессионной моделиd
Анализ коэффициентов уравнения множественной регрессии: ŷx1x2 = 81,03 — 0,41 + 3,37x2 позволяет сделать вывод о степени влияния каждого из двух факторов на показатель производительности труда. Так, параметр a1 = -0,41 свидетельствует о том, что с увеличением продолжительности внутри-сменных простоев на 1 мин следует ожидать снижения производительности труда (дневной выработки деталей одним рабочим) на 0,41 шт. (обратная связь). Повышение же квалификации рабочего на 1 разряд может привести к увеличению выработки на 3,37 детали. Отсюда можно сделать соответствующие практические выводы и осуществить мероприятия, направленные на повышение производительности труда.
Однако на основе коэффициентов регрессии нельзя сказать, какой из факторных признаков оказывает наибольшее влияние на результативный признак, так как коэффициенты регрессии между собой не сопоставимы, поскольку они измерены разными единицами. На их основе нельзя также установить, в развитии каких факторных признаков заложены наиболее крупные резервы изменения результативного показателя, потому что в коэффициентах регрессии не учтена вариация факторных признаков.
Чтобы иметь возможность судить о сравнительной силе влияния отдельных факторов и о тех резервах, которые в них заложены, должны быть вычислены частные коэффициенты эластичности Эi , а также бета-коэффициенты bi и дельта коэффициенты ∆i.
Различия в единицах измерения факторов устраняют с помощью частных коэффициентов эластичности, которые рассчитывают по формуле:
где ai — коэффициент регрессии при I — го факторе;
xi — среднее значение i-го фактора;

Частные коэффициенты эластичности показывают, на сколько процентов в среднем изменяется анализируемый показатель с изменением на 1% каждого фактора при фиксированном положении других факторов.
Для определения факторов, в развитии которых заложены наиболее крупные резервы улучшения изучаемого показателя, необходимо учесть различия в степени варьирования вошедших в уравнение факторов. Это можно сделать с помощью b —коэффициентов, которые вычисляют по формуле:
где σxi — среднее квадратическое отклонение i-го фактора;
σi — среднее квадратическое отклонение показателя.
b — коэффициент показывает, на какую часть среднего квадратического отклонения изменяется результативный признак с
изменением соответствующего факторного признака на величину его среднего квадратического отклонения.
Исходя из соотношения 
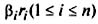
Поделив произведение biri на коэффициент множественной детерминации R 2 , получим коэффициент, который показывает какова доля вклада анализируемого фактора в суммарное влияние всех отобранных факторов. Обозначив этот коэффициент ∆i, получим
Рассчитаем для нашего примера коэффициенты эластичности Эi, а также коэффициенты bi и ∆i , дадим им экономическую интерпретацию:
Анализ частных коэффициентов эластичности показывает, что по абсолютному приросту наибольшее влияние на производительность труда оказывает фактор x2 — повышение квалификации рабочих на 1 % приводит к росту производительности труда на 0,15 %. Снижение же продолжительности внутрисменных простоев на 1% повышает производительность труда только на 0,05%:
Анализ b -коэффициентов показывает, что на производительность труда наибольшее влияние из двух исследуемых факторов с учетом уровня их вариации способен оказать фактор x2 — квалификация рабочих, так как ему соответствует наибольшее (по абсолютной величине) значение b -коэффициента:
На основании анализа ∆i -коэффициентов установлено, что наибольшая доля прироста производительности труда из двух
анализируемых факторов может быть обеспечена развитием такою фактора, как повышение квалификации рабочих.
Таким образом, на основании частных коэффициентов эластичности Эi, bi и ∆i — коэффициентов можно судить о резервах роста производительности труда, которые заложены в том или ином факторе.
Увеличение числа существенных факторов, включаемых в модель исследуемого показателя, позволяет выявить дополнительные резервы производства. Для этого могут быть использованы трех-, четырех- (и т.д.), n-факторные регрессии.
9.3. Непараметрические методы
Применение корреляционного и регрессионного анализа требует, чтобы все признаки были количественно измеренными. Построение аналитических группировок предполагает, что количественным должен быть результативный признак. Параметрические методы основаны на использовании основных количественных параметров распределения (средних величин и дисперсий).
Вместе с тем в статистике применяются также непараметрические методы, с помощью которых устанавливается связь между качественными (атрибутивными) признаками. Сфера их применения шире, чем параметрических, поскольку не требуется соблюдения условия нормальности распределения зависимой переменной, однако при этом снижается глубина исследования связей. При изучении зависимости между качественными признаками не ставится задача представления ее уравнением. Здесь речь идет только об установлении наличия связи и измерении ее тесноты.
В практике статистических исследований приходится иногда анализировать связи между альтернативными признаками, представленными только группами с противоположными (взаимоисключающими) характеристиками. Тесноту связи в этом случае можно оценить, вычислив коэффициент ассоциации.
Для расчета коэффициента ассоциации строится четырехклеточная корреляционная таблица, которая носит название таблицы «четырех полей » и имеет следующий вид:
Применительно к таблице «четырех полей» с частотами lа, b, с и d коэффициент ассоциации выражается формулой:
Коэффициент ассоциации изменяется от -1 до +1; чем ближе к +1 или -1, тем сильнее связаны между собой изучаемые признаки.
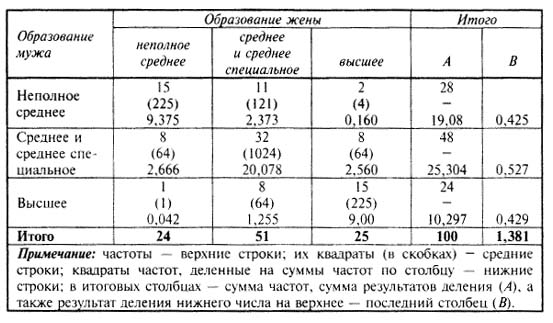
Если ka не менее 0,3 то это свидетельствует о росте отцов и сыновей представленыв табл. 9.5.
Распределение отцов и сыновей по росту, чел.
Посчитаем коэффициент ассоциации по данным табл. 9.5:
Поскольку ka > 0,3, между ростом отцов и сыновей существует корреляционная связь.
Если по каждому из взаимосвязанных признаков выделяется число групп более двух, то для подобного рода таблиц теснота связи между качественными признаками может быть измерена с помощью показателя взаимной сопряженности А. А. Чупрова:
Вычтя из этой суммы единицу, получим φ 2 .
Коэффициент взаимной сопряженности А.А. Чупрова изменяется от 0 до 1, но уже при значении 0,3 можно говорить о тесной связи между вариацией изучаемых признаков.
Его значение показывает заметную связь между уровнями образования мужа и жены при формировании семьи.
Контрольные вопросы
- В чем состоит отличие между функциональной и стохастической связью?
- Что собой представляет корреляционая связь?
- Какими статистическими методами исследуются функциональные и корреляционные связи?
- В чем достоинства и недостатки метода парамельных рядов и аналитических группировок ?
- Какие основные задачи решают с помощью корреляционного и регрессионного анализа ?
- Дайте определение статистической модели.
- Охарактеризуйте основные проблемы и правила построения однофакторной линейной регрессионной модели.
- В чем состоит значение уравнения регрессии ?
- Что характеризуют коэффициенты регрессии?
- Метод определения параметров уравнения регрессии.
- Зачем необходима проверка адекватности регрессионной модели?
- Как осуществляется проверка значимости коэффициентов регрессии ?
- Какими показателями измеряется теснота корреляционной связи?
- Какое значение имеет расчет коэффициента детерминации?
- Линейные коэффициенты корреляции и детерминации, их смысл и назначение.
- Проверка существенности показателей тесноты связи как необходимое условие распространения выводов по результатами выборки на всю генеральную совокупность. Как она осуществляется ?
- Как экономически охарактеризовать однофакторную регрессионную модель ?
- Какой экономический смысл имеют коэффициенты эластичности ?
- В чем преимущество межфакторного регрессионного анализа перед другими методами ?
- Основные проблемы и правила построения многофакторной корреляционной модели.
- Сущность и назначение парных и частных коэффициентов корреляции.
- Сущность и значение совокупного коэффициента множественной корреляции и совокупного коэффициента детерминации.
- Как проверить адекватность уравнения в целом? Значимость коэффициента регрессии? Какие критерии для этого можно использовать?
- Как экономически интерпретировать многофакторную регрессионную модель ?
- Какой экономический смысл имеют коэффициенты эластичности, bi -, ∆i -коэффициенты?
- Каким образом выделить факторы, в изменении которых заложены наибольшие возможности в управлении изменением результативного признака ?
- Какие непараметрические методы применяют для моделирования связи?
РАЗДЕЛ II
МАКРОЭКОНОМИЧЕСКАЯ СТАТИСТИКА
Макроэкономическая статистика является одной из статистических дисциплин прикладного характера. В ней решаются вопросы приложения всей совокупности статистических методов к конкретному объекту исследования.
Объект макроэкономической статистики может быть четко обозначен, исходя из определения предмета статистики, которое дано в курсе теории статистики.
Статистика — комплекс учебных дисцилшн, обеспечивающих овладение методологией статистического исследования массовых социально-экономических явлений и процессов с целью выявления закономерностей их развития в конкретных условиях места и времени.
При конкретизации данного определения применительно к макроэкономической статистике следует исходить из того, что ее объектом изучения являются массовые социально-экономические явления и процессы, совершающиеся на уровне экономики страны в целом.
Макроэкономическая статистика разрабатывает методологию статистического исследования экономических процессов и их развития: систему показателей и методику их расчета, в совокупности обеспечивающих количественную характеристику результатов функционирования экономики страны и регионов в разрезе отраслей, секторов и форм собственности, ее эффективность и уровень жизни населения; использует принятую в международной практике систему национальных счетов в качестве макростатистической модели рыночной экономики.
Являясь самостоятельной научной дисциплиной, макроэкономическая статистика при количественном измерении экономических процессов и явлений основывается на положениях экономической теории, результатах изучения качественных аспектов экономических процессов, полученных в рамках общей экономической теории и различных прикладных ее разделов.
В познании статистических закономерностей и количественной характеристики проявления и действия экономических законов в конкретных условиях места и времени состоит познавательная сила макроэкономической статистики.
С учетом вышеизложенного предлагается следующее определение предмета макроэкономической статистики.
Макроэкономическая статистика — приклодная статистическая дисцилтна, обеспечивающая овладение методологией статистического исследования массовых социально-экономических явлений и процессов с целью выявления закономерностей их развития на макроуровне.
Таким образом, выявление закономерностей поведения макроэкономики требует организации специальной отрасли научных знаний и практической деятельности — макроэкономической статистики, основные аспекты которой рассматриваются ниже.
Глава 10.Статистика населения и трудовых ресурсов
10.1. Показатели численности населения, методы их расчета
Население как предмет изучения в статистике представляет собой совокупность людей, проживающих на территории мира, континента, страны или её части, отдельного региона, населенного пункта и непрерывно возобновляющихся за счет рождений и смертей.
Множественная регрессия в EXCEL
history 26 января 2019 г.
- Группы статей
- Статистический анализ
Рассмотрим использование MS EXCEL для прогнозирования переменной Y на основании нескольких переменных Х, т.е. множественную регрессию.
Перед прочтением этой статьи рекомендуется освежить в памяти простую линейную регрессию – прогнозирование на основе значений только одного фактора.
Disclaimer : Данную статью не стоит рассматривать, как пересказ главы из учебника по статистике. Статья не обладает ни полнотой, ни строгостью изложения положений статистической науки. Эта статья – о применении MS EXCEL для целей Множественного регрессионного анализа. Теоретические отступления приведены лишь из соображения логики изложения. Использование данной статьи для изучения Регрессии – плохая идея.
Статья про Множественный регрессионный анализ получилась большая, поэтому ниже для удобства приведены ее разделы:
Прогнозирование единственной переменной Y на основании значений 2-х или более переменных Х называется множественной регрессией .
Множественная линейная регрессионная модель (Multiple Linear Regression Model) имеет вид Y=β 0 +β 1 *X 1 +β 2 *X 2 +…+β k *X k +ε. В этом случае переменная Y зависит от k поясняющих переменных Х, т.е. регрессоров . ε — случайная ошибка . Модель является линейной относительно неизвестных параметров β.
Оценка неизвестных параметров
В этой статье рассмотрим модель с 2-мя регрессорами. Сначала введем необходимые обозначения и понятия множественной регрессии.
Для описания зависимости Y от 2-х переменных линейная модель имеет вид:
Параметры этой модели β i нам неизвестны, но их можно оценить, используя случайную выборку (измеренные значения переменной Y от заданных Х). Оценки параметров модели (β 0 , β 1 , β 2 ) обычно вычисляются методом наименьших квадратов (МНК) , который минимизирует сумму квадратов ошибок прогнозирования (критерий минимизации в англоязычной литературе обозначают как SSE – Sum of Squared Errors).
Ошибка ε имеет случайную природу и имеет свою функцию распределения со средним значением =0 и дисперсией σ 2 .
Оценки b 1 и b 2 называются коэффициентами регрессии , они определяют влияние соответствующей переменной X, когда все остальные независимые переменные остаются неизменными .
Сдвиг (intercept) или постоянный член b 0 , определяет прогнозируемое значение Y, когда все поясняющие переменные Х равны 0 (часто сдвиг не имеет физического смысла в рамках модели и обусловлен лишь математическими вычислениями МНК ).
Вычислив оценки, полученные методом МНК, позволяют прогнозировать значения переменной Y:
Примечание : Для случая 2-х регрессоров, все спрогнозированные значения переменной Y будут лежать в плоскости (в плоскости регрессии ).
В качестве примера рассмотрим технологический процесс изготовления нити:
Инженер, на основе имеющегося опыта, предположил, что прочность нити Y зависит от концентрации исходного раствора (Х 1 ) и температуры реакции (Х 2 ), и соответствует модели линейной регрессии. Для нахождения комбинации переменных Х, при которых Y принимает максимальное значение, необходимо определить коэффициенты регрессии, сделав выборку.
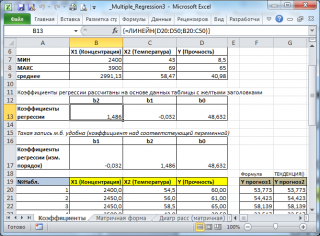
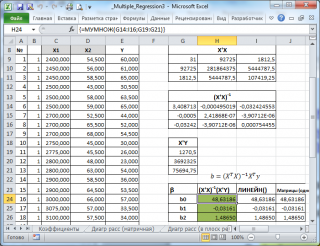
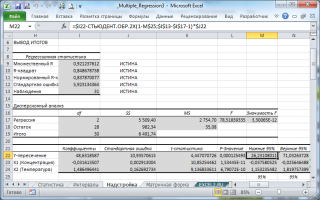
В MS EXCEL коэффициенты множественной регрессии удобнее всего вычислить с помощью функции ЛИНЕЙН() . Это сделано в файле примера на листе Коэффициенты . Чтобы вычислить оценки:
- выделите 3 ячейки в одной строке (т.к. мы рассматриваем случай 2-х регрессоров, то будут вычислены 2 коэффициента регрессии + величина сдвига = 3 значения, для вывода которых понадобится 3 ячейки). Пусть это будет диапазон С8:Е8 ;
- в Строке формул введите = ЛИНЕЙН(D20:D50;B20:C50) . Предполагается, что в столбце В содержатся прогнозируемые значения Y (в нашей модели это Прочность нити), в столбцах С и D содержатся значения контролируемых параметров Х (Х1 – Концентрация в столбце С и Х2 – Температура в столбце D).
- нажмите CTRL+SHIFT+ENTER (т.к. это формула массива ).
В левой ячейке будет рассчитано значение коэффициента регрессии b 2 для переменной Х2, в средней ячейке — значение коэффициента регрессии b 1 для переменной Х1, в правой – сдвиг . Обратите внимание, что порядок вывода коэффициентов регрессии обратный по отношению к расположению столбцов с данными соответствующих переменных Х (вычисленный коэффициент b 2 располагается левее по отношению к b 1 , тогда как значения переменной Х2 располагаются правее значений переменной Х1). Это может привести к путанице, поэтому лучше разместить коэффициенты над соответствующими столбцами с данными, как это сделано в строке 17 файла примера .
Примечание : В принципе без функции ЛИНЕЙН() можно обойтись, записав альтернативные формулы. Для этого в файле примера на листе Коэффициенты в столбцах I : K вычислены отклонения значений переменных Х 1i , Х 2i , Y i от их средних значений 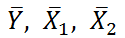
Далее коэффициенты регрессии рассчитываются по следующим формулам (эти формулы справедливы только при прогнозировании по 2-м независимым переменным Х):
При прогнозировании по 3-м и более независимым переменным Х формулы для вычисления коэффициентов регрессии значительно усложняются, поэтому следует использовать матричный подход.
В файле примера на листе Матричная форма выполнены расчеты коэффициентов регрессии с помощью матричного подхода.
Расчет можно произвести как пошагово, так и одной формулой массива :
Коэффициенты регрессии (вектор b ) в этом случае вычисляются по формуле b =(X T X) -1 (X T Y) или в другом виде записи b =(X ’ X) -1 (X ’ Y)
Под Х подразумевается матрица, состоящая из столбцов значений переменной Х с дополнительным столбцом единиц, а под Y – вектор-столбец значений Y.
Диаграмма рассеяния
В случае простой линейной регрессии (один регрессор, т.е. одна переменная Х) для визуализации связи между прогнозируемым значением Y и переменной Х строят диаграмму рассеяния (двумерную).
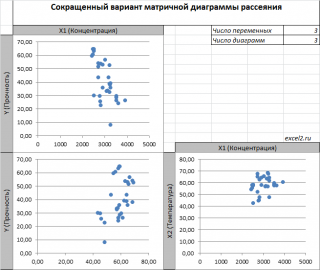
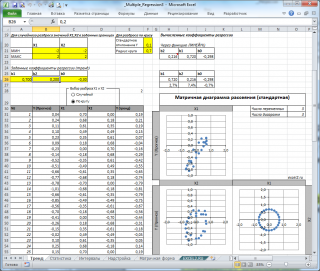
В случае множественной линейной регрессии двумерную диаграмму рассеяния можно построить только для анализа влияния каждого отдельного регрессора на Y (при этом остальные Х не меняются), т.е. так называемую Матричную диаграмму рассеивания (См. файл примера лист Диагр расс (матричная) ).
К сожалению, такую диаграмму трудно интерпретировать.
Более того, матричная диаграмма может вводить в заблуждение (см. Introduction to linear regression analysis / D . C . Montgomery , E . A . Peck , G . G . Vining , раздел 3.2.5 ), демонстрируя наличие или отсутствие линейной взаимосвязи между отдельным регрессором X i и Y.
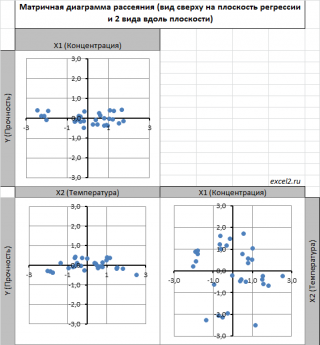
Для случая с 2-мя регрессорами можно предложить альтернативный вид матричной диаграммы рассеяния . В стандартной диаграмме рассеяния строятся проекции на координатные плоскости Х1;Х2, Y;X1 и Y;X2. Однако, если взглянуть на точки относительно плоскости регрессии , то картину, на мой взгляд, будет проще интерпретировать.
Сравним две матричные диаграммы рассеяния (см. файл примера на листе «Диагр расс (в плоск регрессии)» , построенные для одних и тех же наблюдений. Первая – стандартная,
вторая представляет собой вид сверху на плоскость регрессии и 2 вида вдоль плоскости.
На второй диаграмме становится очевидно, что разброс точек относительно плоскости регрессии совсем не большой и поэтому, скорее всего, построенная модель является полезной, а выбранные 2 переменные Х позволяют прогнозировать Y (конечно, для подтверждения этой гипотезы нужно провести процедуру F-теста ).
Несколько слов о построении альтернативной матричной диаграммы рассеяния:
- Перед построением необходимо нормировать значения наблюдений (для каждой переменной вычесть среднее и разделить на стандартное отклонение ). В этом случае практически все точки на диаграммах будут находится в диапазоне +/-3 (по аналогии со стандартным нормальным распределением , 99% значений которого лежат в пределах +/-3 сигма). В этом случае, на диаграмме можно фиксировать мин/макс значений осей, чтобы EXCEL автоматически не модифицировал масштаб осей при изменении данных (это не всегда удобно);
- Теперь координаты точек необходимо рассчитать в системе отсчета относительно плоскости регрессии (в которой плоскость Оху’ совпадает с плоскостью регрессии). Для этого необходимо найти матрицу вращения , например, через вращение приводящее к совмещению нормали к плоскости регрессии и вектора оси Z (0;0;1);
- Новые координаты позволяют построить альтернативную матричную диаграмму. Кроме того, для удобства можно вращать систему координат вокруг новой оси Z, чтобы нагляднее представить себе распределение точек относительно плоскости регрессии (для этого использована Полоса прокрутки в ячейках Q31:S31 ).
Вычисление прогнозных значений Y (отдельное наблюдение и среднее значение) и построение доверительных интервалов
После того, как нами были найдены тем или иным способом коэффициенты регрессии можно приступать к вычислению прогнозных значений Y на основе заданных значений переменных Х.
Уравнение прогнозирования или уравнение регрессии в случае 2-х независимых переменных (регрессоров) записывается в виде:
Примечание: В MS EXCEL прогнозное значение Y для заданных Х 1 и Х 2 можно также предсказать с помощью функции ТЕНДЕНЦИЯ() . При этом 2-й аргумент будет ссылкой на столбцы, содержащие все значения переменных Х 1 и Х 2 , а 3-й аргумент функции должен быть ссылкой на диапазон ячеек, содержащий 2 значения Х (Х 1i и Х 2i ) для выбранного наблюдения i (см. файл примера, лист Коэффициенты, столбец G ). Функция ПРЕДСКАЗ() , использованная нами в простой регрессии, не работает в случае множественной регрессии .
Найдя прогнозное значение Y, мы, таким образом, вычислим его точечную оценку. Понятно, что фактическое значение Y, полученное при наблюдении, будет, скорее всего, отличаться от этой оценки. Чтобы ответить на вопрос о том, на сколько хорошо мы можем предсказывать новые значения Y, нам потребуется построить доверительный интервал этой оценки, т.е. диапазон в котором с определенной заданной вероятностью, скажем 95%, мы ожидаем новое значение Y.
Доверительные интервалы построим при фиксированном Х для:
- нового наблюдения Y;
- среднего значения Y (интервал будет уже, чем для отдельного нового наблюдения)
Как и в случае простой линейной регрессии , для построения доверительных интервалов нам потребуется сначала вычислить стандартную ошибку модели (standard error of the model) , которая приблизительно показывает насколько велика ошибка предсказания значений переменной Y на основании значений переменных Х.
Для вычисления стандартной ошибки оценивают дисперсию ошибки ε, т.е. сигма^2 (ее часто обозначают как MS Е либо MSres ) . Затем, вычислив из полученной оценки квадратный корень, получим Стандартную ошибку регрессии (часто обозначают как SEy или sey ).
где SSE – сумма квадратов значений ошибок модели ei=yi — ŷi ( Sum of Squared Errors ). MSE означает Mean Square of Errors (среднее квадратов ошибок, точнее остатков).
Величина n-p – это количество степеней свободы ( df – degrees of freedom ), т.е. число параметров системы, которые могут изменяться независимо (вспомним, что у нас в этом примере есть n независимых наблюдений переменной Y, р – количество оцениваемых параметров модели). В случае простой множественной регрессии с 2-мя регрессорами число степеней свободы равно n-3, т.к. при построении плоскости регрессии было оценено 3 параметра модели b (т.е. на это было «потрачено» 3 степени свободы ).
В MS EXCEL стандартную ошибку SEy можно вычислить формулы (см. файл примера, лист Статистика ):
Стандартная ошибка нового наблюдения Y при заданных значениях Х (вектор Хi) вычисляется по формуле:
x i — вектор-столбец со значениями переменных Х (с дополнительной 1) для заданного наблюдения i.
Соответствующий доверительный интервал вычисляется по формуле:
где α (альфа) – уровень значимости (обычно принимают равным 0,05=5%)
р – количество оцениваемых параметров модели (в нашем случае = 3)
n-p – число степеней свободы
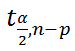
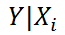
Стандартная ошибка среднего значения Y при заданных значениях Х (вектор Хi) будет меньше, чем стандартная ошибка отдельного наблюдения. Вычисления производятся по формуле:
x i — вектор-столбец со значениями переменных Х (с дополнительной 1) для заданного наблюдения i.
Соответствующий доверительный интервал вычисляется по формуле:
Прогнозное значение Yi (точечная оценка) используется тоже, что и для отдельного наблюдения.
Стандартные ошибки и доверительные интервалы для коэффициентов регрессии
В разделе Оценка неизвестных параметров мы получили точечные оценки коэффициентов регрессии . Так как эти оценки получены на основе случайных величин (значений переменных Х и Y), то эти оценки сами являются случайными величинами и соответственно имеют функцию распределения со средним значением и дисперсией . Но, чтобы перейти от точечных оценок к интервальным , необходимо вычислить соответствующие стандартные ошибки (т.е. стандартные отклонения ) коэффициентов регрессии .
Стандартная ошибка коэффициента регрессии b j (обозначается se ( b j ) ) вычисляется на основании стандартной ошибки по следующей формуле:
где C jj является диагональным элементом матрицы (X ’ X) -1 . Для коэффициента сдвига b 0 индекс j=1 (верхний левый элемент), для b 1 индекс j=2, b 2 индекс j=3 (нижний правый элемент).
SEy – стандартная ошибка регрессии (см. выше ).
В MS EXCEL стандартные ошибки коэффициентов регрессии можно вычислить с помощью функции ЛИНЕЙН() :
Примечание : Подробнее о функции ЛИНЕЙН() см. статью Функция MS EXCEL ЛИНЕЙН() .
Применяя матричный подход стандартные ошибки можно вычислить и через обычные формулы (точнее через формулу массива , см. файл примера лист Статистика ):
= КОРЕНЬ(СУММКВРАЗН(E13:E43;F13:F43) /(n-p)) *КОРЕНЬ (ИНДЕКС (МОБР (МУМНОЖ(ТРАНСП(B13:D43);(B13:D43)));j;j))
При построении двухстороннего доверительного интервала для коэффициента регрессии его границы определяются следующим образом:
где t – это t-значение , которое можно вычислить с помощью формулы = СТЬЮДЕНТ.ОБР.2Х(0,05;n-p) для уровня значимости 0,05.
В результате получим, что найденный доверительный интервал с вероятностью 95% (1-0,05) накроет истинное значение коэффициента регрессии b j . Здесь мы считаем, что коэффициент регрессии b j имеет распределение Стьюдента с n-p степенями свободы (n – количество наблюдений, т.е. пар Х и Y).
Проверка гипотез
Когда мы строим модель, мы предполагаем, что между Y и переменными X существует линейная взаимосвязь. Однако, как это иногда бывает в статистике, можно вычислять параметры связи даже тогда, когда в действительности она не существует, и обусловлена лишь случайностью.
Единственный вариант, когда Y не зависит X, возможен, когда все коэффициенты регрессии β равны 0.
Чтобы убедиться, что вычисленная нами оценка коэффициентов регрессии не обусловлена лишь случайностью (они не случайно отличны от 0), используют проверку гипотез . В качестве нулевой гипотезы Н 0 принимают, что линейной связи нет, т.е. ВСЕ β=0. В качестве альтернативной гипотезы Н 1 принимают, что ХОТЯ БЫ ОДИН коэффициент β <>0.
Процедура проверки значимости множественной регрессии, приведенная ниже, является обобщением дисперсионного анализа , использованного нами в случае простой линейной регрессии (F-тест) .
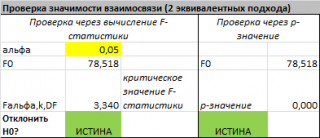
Если нулевая гипотеза справедлива, то тестовая F -статистика имеет F-распределение со степенями свободы k и n — k -1 , т.е. F k, n-k-1 :
Проверку значимости регрессии можно также осуществить через вычисление p -значения . В этом случае вычисляют вероятность того, что случайная величина F примет значение F 0 (это и есть p-значение ), затем сравнивают p-значение с заданным уровнем значимости α (альфа) . Если p-значение больше уровня значимости , то нулевую гипотезу нет оснований отклонить, и регрессия незначима.
В MS EXCEL значение F 0 можно вычислить на основании значений выборки по вышеуказанной формуле или с помощью функции ЛИНЕЙН() :
В MS EXCEL для проверки гипотезы через p -значение используйте формулу =F.РАСП.ПХ(F 0 ;k;n-k-1) файл примера лист Статистика , где показано эквивалентность обоих подходов проверки значимости регрессии).
В MS EXCEL критическое значение для заданного уровня значимости F 1-альфа, k, n-k-1 можно вычислить по формуле = F.ОБР(1- альфа;k;n-k-1) или = F.ОБР.ПХ(альфа;k; n-k-1) . Другими словами требуется вычислить верхний альфа- квантиль F -распределения с соответствующими степенями свободы .
Таким образом, при значении статистики F 0 > F 1-альфа, k, n-k-1 мы имеем основание для отклонения нулевой гипотезы.
В программах статистики результаты процедуры F -теста выводят с помощью стандартной таблицы дисперсионного анализа . В файле примера такая таблица приведена на листе Надстройка , которая построена на основе результатов, возвращаемых инструментом Регрессия надстройки Пакета анализа MS EXCEL .
Генерация данных для множественной регрессии с помощью заданного тренда
Иногда, бывает удобно сгенерировать значения наблюдений, имея заданный тренд.
Для решения этой задачи нам потребуется:
- задать значения регрессоров в нужном диапазоне (значения переменных Х);
- задать коэффициенты регрессии ( b );
- задать тренд (вычислить значения Y= b0 +b1 * Х 1 + b2 * Х 2 );
- задать величину разброса Y вокруг тренда (варианты: случайный разброс в заданных границах или заданная фигура, например, круг)
Все вычисления выполнены в файле примера, лист Тренд для случая 2-х регрессоров. Там же построены диаграммы рассеяния .
Коэффициент детерминации
Коэффициент детерминации R 2 показывает насколько полезна построенная нами линейная регрессионная модель .
По определению коэффициент детерминации R 2 равен:
R 2 = Изменчивость объясненная моделью ( SSR ) / Общая изменчивость ( SST ).
Этот показатель можно вычислить с помощью функции ЛИНЕЙН() :
При добавлении в модель новой объясняющей переменной Х, коэффициент детерминации будет всегда расти. Поэтому, рост коэффициента детерминации не может служить основанием для вывода о том, что новая модель (с дополнительным регрессором) лучше прежней.
Более подходящей статистикой, которая лишена указанного недостатка, является нормированный коэффициент детерминации (Adjusted R-squared):
где p – число независимых регрессоров (вычисления см. файл примера лист Статистика ).
http://helpiks.org/2-35593.html
http://excel2.ru/articles/mnozhestvennaya-regressiya-v-ms-excel