Решения задач: линейная регрессия и коэффициент корреляции

Парная линейная регрессия — это зависимость между одной переменной и средним значением другой переменной. Чаще всего модель записывается как $y=ax+b+e$, где $x$ — факторная переменная, $y$ — результативная (зависимая), $e$ — случайная компонента (остаток, отклонение).

В учебных задачах по математической статистике обычно используется следующий алгоритм для нахождения уравнения регрессии.

1. Выбор модели (уравнения). Часто модель задана заранее (найти линейную регрессию) или для подбора используют графический метод: строят диаграмму рассеяния и анализируют ее форму.
2. Вычисление коэффициентов (параметров) уравнения регрессии. Часто для этого используют метод наименьших квадратов.
3. Проверка значимости коэффициента корреляции и параметров модели (также для них можно построить доверительные интервалы), оценка качества модели по критерию Фишера.
4. Анализ остатков, вычисление стандартной ошибки регрессии, прогноз по модели (опционально).

Ниже вы найдете решения для парной регрессии (по рядам данных или корреляционной таблице, с разными дополнительными заданиями) и пару задач на определение и исследование коэффициента корреляции.

Примеры решений онлайн: линейная регрессия

Простая выборка

Пример 1. Имеются данные средней выработки на одного рабочего Y (тыс. руб.) и товарооборота X (тыс. руб.) в 20 магазинах за квартал. На основе указанных данных требуется:
1) определить зависимость (коэффициент корреляции) средней выработки на одного рабочего от товарооборота,
2) составить уравнение прямой регрессии этой зависимости.

Пример 2. С целью анализа взаимного влияния зарплаты и текучести рабочей силы на пяти однотипных фирмах с одинаковым числом работников проведены измерения уровня месячной зарплаты Х и числа уволившихся за год рабочих Y:
X 100 150 200 250 300
Y 60 35 20 20 15
Найти линейную регрессию Y на X, выборочный коэффициент корреляции.

Пример 3. Найти выборочные числовые характеристики и выборочное уравнение линейной регрессии $y_x=ax+b$. Построить прямую регрессии и изобразить на плоскости точки $(x,y)$ из таблицы. Вычислить остаточную дисперсию. Проверить адекватность линейной регрессионной модели по коэффициенту детерминации.

Пример 4. Вычислить коэффициенты уравнения регрессии. Определить выборочный коэффициент корреляции между плотностью древесины маньчжурского ясеня и его прочностью.
Решая задачу необходимо построить поле корреляции, по виду поля определить вид зависимости, написать общий вид уравнения регрессии Y на Х, определить коэффициенты уравнения регрессии и вычислить коэффициенты корреляции между двумя заданными величинами.

Пример 5. Компанию по прокату автомобилей интересует зависимость между пробегом автомобилей X и стоимостью ежемесячного технического обслуживания Y. Для выяснения характера этой связи было отобрано 15 автомобилей. Постройте график исходных данных и определите по нему характер зависимости. Рассчитайте выборочный коэффициент линейной корреляции Пирсона, проверьте его значимость при 0,05. Постройте уравнение регрессии и дайте интерпретацию полученных результатов.

Корреляционная таблица

Пример 6. Найти выборочное уравнение прямой регрессии Y на X по заданной корреляционной таблице

Пример 7. В таблице 2 приведены данные зависимости потребления Y (усл. ед.) от дохода X (усл. ед.) для некоторых домашних хозяйств.
1. В предположении, что между X и Y существует линейная зависимость, найдите точечные оценки коэффициентов линейной регрессии.
2. Найдите стандартное отклонение $s$ и коэффициент детерминации $R^2$.
3. В предположении нормальности случайной составляющей регрессионной модели проверьте гипотезу об отсутствии линейной зависимости между Y и X.
4. Каково ожидаемое потребление домашнего хозяйства с доходом $x_n=7$ усл. ед.? Найдите доверительный интервал для прогноза.
Дайте интерпретацию полученных результатов. Уровень значимости во всех случаях считать равным 0,05.

Пример 8. Распределение 100 новых видов тарифов на сотовую связь всех известных мобильных систем X (ден. ед.) и выручка от них Y (ден.ед.) приводится в таблице:
Необходимо:
1) Вычислить групповые средние и построить эмпирические линии регрессии;
2) Предполагая, что между переменными X и Y существует линейная корреляционная зависимость:
А) найти уравнения прямых регрессии, построить их графики на одном чертеже с эмпирическими линиями регрессии и дать экономическую интерпретацию полученных уравнений;
Б) вычислить коэффициент корреляции, на уровне значимости 0,05 оценить его значимость и сделать вывод о тесноте и направлении связи между переменными X и Y;
В) используя соответствующее уравнение регрессии, оценить среднюю выручку от мобильных систем с 20 новыми видами тарифов.

Коэффициент корреляции

Пример 9. На основании 18 наблюдений установлено, что на 64% вес X кондитерских изделий зависит от их объема Y. Можно ли на уровне значимости 0,05 утверждать, что между X и Y существует зависимость?

Пример 10. Исследование 27 семей по среднедушевому доходу (Х) и сбережениям (Y) дало результаты: $\overline=82$ у.е., $S_x=31$ у.е., $\overline=39$ у.е., $S_y=29$ у.е., $\overline =3709$ (у.е.)2. При $\alpha=0,05$ проверить наличие линейной связи между Х и Y. Определить размер сбережений семей, имеющих среднедушевой доход $Х=130$ у.е.

ТЕМА 1. Парная линейная регрессия.

Аналитический метод выбора функциональной зависимости сводится к попытке выяснения содержательного смысла зависимости изучаемого показателя от объясняющего фактора и последующего выбора на этой основе соответствующей функциональной зависимости.

Временной (динамический) ряд (time-seriesdata) — выборка, в которой важны не только сами наблюдаемые значения, но и порядок их следования друг за другом. Чаще всего данные представляют собой наблюдения одной и той же величины в последовательные моменты времени.

Выборочная остаточная дисперсия — статистика, которая является несмещенной оценкой теоретической остаточной дисперсии σ 2 и определяется формулой

Выборочный коэффициент парной корреляции определяется по формуле

где — выборочные дисперсии x и y , соответственно.

Геометрический метод выбора функциональной зависимости сводится к следующему. На координатной плоскости Oxy наносятся точки (x_i,y_i), i=1. n, соответствующие выборке. Полученное графическое изображение называется полем корреляции (диаграммой рассеяния).

Достоверным событием называется некоторое событие, которое обязательно происходит в условиях данного эксперимента.

Задача эконометрического моделирования: На основании экспериментальных данных определить (оценить) объясненную часть зависимой переменной и, рассматривая случайную составляющую как случайную величину, получить оценки параметров ее распределения.

Коэффициент детерминации определяется по формуле:

Величина коэффициента детерминации представляет собой долю вариации зависимой переменной, обусловленную вариацией объясняющей переменной.

Метод наименьших квадратов (МНК). Согласно методу наименьших квадратов значения параметров функции (будем обозначать их через a,b) выбираются таким образом, чтобы сумма квадратов отклонений выборочных значений y_i от значений была минимальной

где минимум ищется по параметрам a, b, которые входят в зависимость .

Модель линейной парной регрессии — y=α+βx+ε.

Объясняющие переменные (факторы) — переменные (факторы) от которых зависят зависимые (объесняемые) переменные.

Основная задача эконометрического моделирования — построение по выборке эмпирической модели, выборочной парной регрессии , являющейся оценкой теоретической регрессии (функции f(x) ):, здесь — эмпирическая (выборочная) регрессия, описывающая усредненную по x зависимость между изучаемым показателем и объясняющим фактором.

Основные этапы эконометрического моделирования и анализа:

• Постановочный — формируется цель исследования (анализ экономического объекта, прогноз его показателей, имитация развития, выработка управленческих решений), теоретическое обоснование выбора переменных;
• Априорный — анализ сущности изучаемого объекта, формирование и формализация имеющейся информации;
• Параметризация — выбор вида модели (вида функции f(X)), анализ взаимосвязей и спецификация модели;
• Информационный — сбор необходимой статистической информации — наблюдаемых значений переменных;
• Идентификация модели — статистический анализ модели и оценка ее параметров;
• Верификация модели — проверка адекватности, статистической значимости модели.

Оценка теоретическое регрессии линейной парной регрессии строится в виде: =a+bx, где a, b являются оценками параметров α, β теоретической регрессии.

Оценками неизвестных параметров регрессии по методу наименьших квадратов (оценками МНК) называются значения параметров a и b, которые минимизируют сумму квадратов отклонений выборочных значений у_i от значений .

Пространственная выборка (cross-sectional data) — набор экономических показателей, полученных в некоторый момент времени (или в относительно небольшом промежутке времени), т. е. набор независимых выборочных данных из некоторой генеральной совокупности (так как практически независимость случайных величин проверить трудно, то обычно за независимые принимаются величины, не связанные причинно);

Спецификация модели — формулировка исходных предпосылок и ограничений, выбор структуры уравнения модели, представление в математической форме обнаруженных взаимосвязей и соотношений, установление состава объясняющих переменных.

Средняя ошибка аппроксимации регрессии по формуле определяется по формуле:

Значение этой ошибки в пределах 5-7% свидетельствует о хорошем соответствии модели эмпирическим данным.

Статическая (стохастическая, вероятностная) зависимость — форма связи между переменными величинами, когда каждому значению одной переменной соответствует не какое-то определенное значение другой переменной, а множество возможных значений (более точно — некоторое условное распределение) другой переменной.

Теорема Гаусса-Маркова . Если регрессионная модель y=α+βx+ε удовлетворяет условиям Гаусса-Маркова, то оценки МНК a и b имеют наименьшую дисперсию в классе всех линейных несмещенных оценок.

Теоретическое уравнение регрессии — E_X(y)=f(X), где f(X) — теоретическая функция регрессии.

Уравнение регрессионной модели — y= E_X(y)+ε

• Величины ε_i являются случайными.
• Математическое ожидание возмущений равно нулю: E(ε_i)=0.
• Возмущения ε_i и ε_j некоррелированы: E(ε_iε_j)=0, i ≠ j.
• Дисперсия возмущения ε_i постоянна для каждого i: D(ε_i)=σ 2 . Это условие называется условием гомоскедастичности. Нарушение этого условия называется гетероскедастичностью.
• Величины ε_i взаимно независимы со значениями объясняющих переменных.
  Здесь, во всех условиях i=1,2. n.

Эконометрика — это раздел математики, занимающийся разработкой и применением статистических методов для измерений взаимосвязей между экономическими переменными.

Эконометрическая модель — y=f(X)+ε, y — зависимая переменная, X=(x₁,x₂. x_k) — объясняющие переменные, f(X) — объясненная часть, ε — случайная составляющая (возмущение или ошибка).

Эмпирическое уравнение регрессии (модельная функция регрессии) — y=f(X,B).

Эмпирический метод выбора функциональной зависимости состоит в следующем. Выбирается некоторая параметрическая функциональная зависимость f(x).

ТЕМА 2. Множественная линейная регрессия.

Выборочная остаточная дисперсия — статистика, вычисляемая по правилу , где n — число наблюдений, k — число факторов модели.

Выборочный коэффициент частной корреляции (частный коэффициент корреляции) между зависимыми переменными x_i и x_j используется для оценки взаимосвязи этих переменных, «очищенной» от влияния других факторов (см. § 2.4).

Качественный признак — признак, имеющий несколько значений.

Классическая нормальная линейная модель множественной регрессии

Модель множественной линейной регрессии Y=Xβ+ε, удовлетворяющая условиям Гаусса-Маркова, называется классической нормальной линейной моделью множественной регрессии , в предположении, что ε — нормально распределенный случайный вектор.

Коэффициент детерминации (множественный) является мерой адекватности регрессионной модели и определяется по формуле , где — сумма квадратов отклонений, обусловленная регрессией, — остаточная сумма квадратов, представляет собой общую сумму квадратов отклонений зависимой переменной от средней.

Коэффициент эластичности (частный коэффициент эластичности) используют для сравнения влияния на зависимую переменную различных объясняющих переменных. Он показывает, на сколько процентов изменится в среднем y при увеличении только переменной x_i на 1% и неизменных значениях остальных переменных.

Ловушкой фиктивных переменных называют ситуацию, когда сумма фиктивных переменных тождественно равна константе.

Модель множественной линейной регрессии имеет вид y_i=α+β₁x_i1+. +β_kx_ik+ε, , что в матричной форме может быть записано Y=Xβ+ε, где , x_ij — i-е наблюдение объясняющей переменной x_j, n — объем выборки,k — число факторов.

Под мультиколлинеарностью понимается высокая взаимная коррелированность объясняющих переменных. Мультиколлинеарность может проявляться в двух формах: функциональной и стохастической.

Оценками неизвестных параметров α, β₁, β₂. β_k линейной множественной регрессии по методу наименьших квадратов (оценками МНК) называются значения параметров a,b₁,b₂. b_k, минимизирующие сумму квадратов отклонений выборочных значений у_i от расчетных значений (см. §2.2).

Правило введения фиктивных переменных: если качественный признак имеет p альтернативных значений (градаций), то число бинарных фиктивных переменных должно быть равно p-1.

Регрессионные уравнения с переменной структурой — модели, в которых качественные признаки существенно влияют на структуру линейных связей между переменными.

Скорректированный (исправленный) коэффициент детерминации определяется формулой: .

Стандартизованный коэффициент регрессии , используют для сравнения влияния на зависимую переменную различных объясняющих переменных. Он показывает, на сколько величин s_y изменится в среднем зависимая переменная y при увеличении только i-ой переменной на .

Стандартная ошибка m_a коэффициента a вычисляется по правилу , где — первый элемент, стоящий на главной диагонали матрицы (X T X) -1 .

Стандартная ошибка коэффициента b_i вычисляется по правилу .

Стохастическая (неполная, несовершенная) форма мультиколлинеарности имеет место в случае, когда хотя бы между двумя объясняющими переменными имеется достаточно высокая степень корреляции.

Если выполнены условия Гаусса-Маркова, то оценки метода наименьших квадратов параметров модели линейной множественной регрессии являются наиболее эффективными (в смысле минимума дисперсии линейных комбинаций оценок параметров) в классе линейных несмещенных оценок.

Фиктивная (искусственная) переменная — переменная, описывающая количественным образом различные состояния качественного признака.

Функциональная (полная, совершенная) форма мультиколлинеарности — форма мультиколлинеарности, при которой, по крайней мере, между двумя объясняющими переменными существует линейная зависимость.

Эконометрическая модель множественной регрессии — y=f(x₁,x₂. x_k)+ε, где f(x₁,x₂. x_k) — неизвестная функциональная зависимость (теоретическая регрессия); ε — случайное слагаемое (возмущение), представляющее собой совокупное действие не включенных в модель факторов, ошибки измерения.

Эмпирическая (выборочная) множественная линейная регрессия имеет вид: , где a,b₁,b₂. b_k являются оценками параметров α, β₁, β₂,. β_k теоретической регрессии.

Эмпирическая (выборочная) регрессия — оценка теоретической регрессии (функции f(x₁,x₂. x_k)), описывающая усредненную зависимость между изучаемым показателем и факторами.

ТЕМА 3. Гетероскедастичность и автокоррелированность остатков.

Под автокорреляцией (сериальной, последовательной корреляцией) понимается корреляция между наблюдаемыми показателями, упорядоченными определенным образом.

Автокорреляция первого порядка — тип автокорреляции, для которого наибольшее влияние на наблюдение оказывает результат предыдущего наблюдения.

Гетероскедастичности условие — условие непостоянства дисперсий возмущений.

Гомоскедастичности условие — условие постоянства дисперсий возмущений.

Классическая регрессионная модель

Модель множественной линейной регрессии Y=Xβ+ε, удовлетворяющая условиям Гаусса-Маркова, называется классической регрессионной моделью .

Коэффициент автокорреляции первого порядка — парный коэффициент корреляции между рядами e₁, e₂. e_n-1 и e₂, e₃. e_n, вычисляемый по формуле .

Лаговые переменные — факторы, влияние которых характеризуется определенным запаздыванием.

Модели с гетероскедастичностью — регрессионные модели, для которых дисперсии возмущений не одинаковы.

Модели с корреляцией ошибок — регрессионные модели, для которых наблюдаемые значения зависимой переменной коррелируют со значениями в предыдущие моменты времени, т.е. имеет место корреляция между различными возмущениями.

Обобщенная линейная модель множественной регрессии имеет вид Y=Xβ+ε, где переменые Y — вектор зависимых переменных размера (nx1), X — (nxk) матрица объясняющих переменных, β — (kx1) вектор параметров регрессии, ε — (nx1) вектор случайных возмущений, причем предполагаются выполненными условия:

1. Вектор возмущений ε=(ε₁. ε_n) является случайным вектором.
2. E(ε)=0_n (0_n — нулевой вектор размера n).
3. Σ_ε= E(εε T )=Ω, где Ω — положительно определнная матрица.
4. Величины ε_i взаимно независимы со значениями объясняющих переменных.
5. r(X)=k+1.

Обобщенный метод наименьших квадратов (ОМНК) — способ оценивания вектора коэффициентов регрессионного уравнения, при котором оценка зависит от матрицы ковариации ошибок.

Отрицательная автокорреляция имеет место, если r(ε_t-1,ε_t) Положительная автокорреляция имеет место, если r(ε_t-1,ε_t)>0.

Статистика Дарбина-Уотсона используется в тесте Дарбина-Уотсона для оценки корреляции остатков и вычисляется

В классе линейных несмещенных оценок вектора β для обобщенной регрессионной модели оценка имеет наименьшую матрицу ковариаций.

Тест Дарбина-Уотсона является критерием обнаружения автокорреляции первого порядка (см. §3.3.1).

Тест Голдфелда-Квандта позволяет определить наличие гетероскедастичности (см. §3.2.2).

Тест ранговой корреляции Спирмена позволяет определить наличие гетероскедастичности (см. §3.2.1).

ТЕМА 4. Нелинейные модели и их линеаризация.

Абсолютная ошибка аппроксимации используется для оценки качества нелинейной регрессии и вычисляется следующим образом:

Двойная логарифмическая модель — линейная модель, в которой и зависимая и объясняющая переменные заданы в логарифмической виде .

Индекс корреляции используется для оценки качества нелинейной регрессии и вычисляется следующим образом:

Коэффициент эластичности характеризует влияние фактора на зависимую переменную и вычисляется по формуле .

Линейно логарифмические (полулогарифмические) модели — нелинейные по объясняющим переменным, но линейные по оцениваемым параметрам модели, имеющие вид: .

Логарифмически линейная (логлинейная) модель — нелинейная модель вида lny= α+βx+ε.

Модель с квадратными корнями — нелинейная по объясняющим переменным, но линейная по оцениваемым параметрам модель, имеющая вид: .

Обратная (гиперболическая) модель — нелинейная по объясняющим переменным, но линейная по оцениваемым параметрам модель, имеющая вид: .

Показательная (экспоненциальная) модель — нелинейная модель вида y=αe βx ε.

Полиномиальная модель — нелинейная по объясняющим переменным, но линейная по оцениваемым параметрам модель, имеющая вид:

Среднее абсолютное отклонение используется для оценки качества нелинейной регрессии и вычисляется следующим образом:

Стандартная ошибка регрессии (среднее квадратическое отклонение) используется для оценки качества нелинейной регрессии и вычисляется следующим образом:

Степенная модель — нелинейная по объясняющим переменным, но линейная по оцениваемым параметрам модель, имеющая вид:

ТЕМА 5. Системы линейных уравнений.

Двухшаговый метод наименьших квадратов – метод построения оценок структурных коэффициентов, основанный на методе инструментальных переменных (см. §5.2).

Идентифицируемость – возможность определения структурных коэффициентов уравнения по коэффициентам приведенной формы.

Идентифицируемое уравнение – уравнение, все входящие структурные параметры которого идентифицируемы.

Идентифицируемый параметр – структурный параметр, который может быть однозначно оценен с помощью косвенного метода наименьших квадратов.

Инструментальные переменные – новые переменные, которые тесно коррелируют с исходными регрессорами и не коррелируют со случайными составляющими.

Косвенный метод наименьших квадратов – метод построения оценок структурных коэффициентов с помощью оценок коэффициентов приведенной формы (см. §5.1).

Лагированные переменные (эндогенные переменные с лагом) — эндогенные переменные, относящиеся к предыдущим моментам времени.

Метод инструментальных переменных – один из самых распространенных методов оценивания уравнений, в которых регрессоры коррелируют со случайными компонентами (см. §5.2).

Неидентифицируемый параметр – структурный параметр, значение которого нельзя определить, даже зная точные значения параметров приведенной формы.

Предопределенными переменными называют экзогенные переменные и эндогенные переменные с лагом.

Приведенная форма системы одновременных уравнений – разрешенная относительно эндогенных переменных система уравнений в структурной форме, в правых частях новых уравнений которой останутся только экзогенные переменные:

Порядковые условия – необходимые условия, используемые для проверки идентифицируемости структурных уравнений (см. §5.3).

Сверхидентифицируемый параметр – структурный параметр, которому косвенный метод наименьших квадратов дает несколько различных его оценок, то есть существует несколько значений структурного коэффициента, соответствующих найденным значениям приведенных коэффициентов.

Система линейных одновременных уравнений записывается таким образом, что в левых частях уравнений будут выделены эндогенные переменные, рассматриваемые как объясняемые переменные, в правой части будет представлена зависимость этих переменных от экзогенных переменных и оставшихся эндогенных.

Структурная форма системы линейных одновременных уравнений имеет вид

то есть, эндогенных переменных в такой системе столько же, сколько и уравнений, но в отдельном уравнении их может быть несколько. В каждом уравнении, взятом в отдельности, только одна переменная, помещенная в левую часть, может рассматриваться как объясняемая, а остальные эндогенные переменные в этом уравнении являются регрессорами, причем коррелирующими со случайным возмущением.

Структурные параметры – параметры системы линейных одновременных уравнений, записанной в структурной форме.

Трехшаговый метод наименьших квадратов – метод построения оценок структурных коэффициентов, сочетающий процедуру одновременного оценивания и метод инструментальных переменных (см. §5.2).

Экзогенные переменные — переменные, определяемые вне системы.

Эндогенные переменные — переменные, определяемые внутри системы.

ТЕМА 6. Временные ряды.

Авторегрессионная модель скользящей средней порядков p и q соответственно имеет вид

Авторегрессионная модель p-го порядка описывает изучаемый показатель в момент t в зависимости от его значений в предыдущие моменты y_t-1, y_t-2. y_t-p и имеет вид:

Авторегрессионные модели – модели, в которых в качестве лаговых переменных участвуют значения зависимых переменных.

Аддитивная модель временного ряда представляется в виде суммы компонент: y_t=u_t+s_t+v_t+ε_t.

Временной (динамический) ряд – последовательность наблюдений некоторого признака, упорядоченных в порядке возрастания моментов времени.

Выборочный коэффициент автокорреляции определяется по формуле

Гипотеза случайности значений ряда наблюдений – гипотеза о независимости и стационарности распределения наблюдений, образующих временной ряд.

Коррелограмма – график выборочной автокорреляционной функции .

Критерий «восходящих и нисходящих» серий – критерий, согласно которому проверяется гипотеза случайности (см. §6.2.2).

Критерий серий, основанный на медиане выборки – критерий, согласно которому проверяется гипотеза случайности (см. §6.2.1).

Лаговые переменные — переменные, влияние которых характеризуется некоторым запаздыванием.

Метод аналитического выравнивания используется для оценки тренда и периодической составляющей временного ряда (см. §6.3).

Методы сглаживания временного ряда используются для оценки тренда и периодической составляющей временного ряда и делятся на:

• сглаживание с помощью скользящей средней (см. §6.4);
• сглаживание с помощью простой скользящей средней (см. §6.4);
• сглаживание с помощью взвешенной скользящей средней (см. §6.4);
• сглаживание с помощью скользящей медианы (см. §6.4);
• экспоненциальное сглаживание (см. §6.5).

Модели с лагами (распределенными лагами) – динамическая модели, содержащие в качестве лаговых переменных только независимые (объясняющие) переменные.

Модель скользящей средней q-го порядка имеет вид:

Мультипликативная модель временного ряда представляется в виде произведения компонент: y_t=u_t× s_t× v_t× ε_t.

Сезонная компонента s_t уровней временного ряда – компонента уровней временного ряда, отражающая повторяемость экономических процессов в течение не слишком длительного периода.

Случайная компонента ε_t уровней временного ряда – компонента уровней временного ряда, отражающая влияние случайных, а также неучтенных факторов.

Стационарный временной ряд – временной ряд y_t, вероятностные свойства которого (закон распределения y_t и его числовые характеристики) не зависят от момента времени t.

Тренд u_t уровней временного ряда – плавно меняющаяся компонента уровней временного ряда, отражающая влияние долговременных, систематических факторов, основную тенденцию в формировании рассматриваемого показателя.

Уровни ряда – отдельные наблюдения y_t, t=1,2. n (где n – число наблюдений).

Циклическая компонента v_t уровней временного ряда – компонента уровней временного ряда, отражающая повторяемость экономических процессов в течение длительных периодов.

Выборочное уравнение регрессии

Две случайные величины могут быть связаны либо функциональной зависимостью, либо статистической зависимостью, либо быть независимыми. Строгая функциональная зависимость реализуется редко, так как обе или одна из двух величин подвержены еще воздействию случайных факторов. Причем среди этих факторов могут быть и общие для обеих величин, т.е. воздействующие на обе случайные величины. В этих случаях возникает статистическая зависимость.

Статистическойназывается зависимость, при которой изменение одной из величин влечет изменение распределения другой. В частности, изменение одной из величин вызывает изменение среднего значения другой. В этом случае статистическая зависимость называется корреляционной.Например, связь между количеством удобрений и урожаем, между вложенными средствами и прибылью.

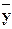
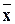
Среднее арифметическое наблюдавшихся значений случайной величины Y , соответствующих значению X=x, называется условным средним _xи является точечной оценкой математического ожидания. Аналогично определяется условное среднее _y .

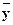
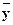
Условное математическое ожидание M ( Y | x )является функцией отx,следовательно, его оценка, т.е. условное среднее _x,также функция от x:

_x = f*(x).

Это уравнение называется выборочным уравнением регрессии Y на X. Функцию f*(x)называют выборочной регрессией, а ее график – выборочной линией регрессии Y на X . Аналогично уравнение

_y = φ * (y),

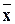
функцию φ * (y) и ее график называют выборочным уравнением регрессии, выборочной регрессией и выборочной линией регрессии X на Y .

Отыскание параметров функций f*(x)и φ * (y), если вид их известен, оценка тесноты связи между величинами X и Y – задачи корреляционного анализа.Задачей регрессионного анализа есть оценка параметров функции регрессии β_i и остаточной дисперсии σ_ост 2 .

Остаточная дисперсия – та часть рассеивания Y , которую нельзя объяснить действием X. σ_ост 2 может служить для оценки точности подбора функции регрессии и полноты набора признаков, включенных в анализ. Вид зависимости g(x) выбирают, исходя из характера поля корреляции и природы процесса.

Оценкой коэффициента линейной регрессии β является выборочный коэффициент регрессии Y на X r_yx. Значения параметра r_yxи параметра b уравнения прямой линии регрессии

Y = r_yx x + b

подбираются таким образом, чтобы точки (x₁,y₁), (x₂,y₂),…,(x_n,y_n), построенные по данным наблюдений, на плоскости xOy лежали как можно ближе к прямой линии регрессии. Это равносильно требованию, чтобы сумма квадратов отклонений функции Y(x_i) от y_i была минимальной. В этом суть МНК.

Выборочное уравнение прямой линии регрессии Y на X может быть записано в таком виде:

_x – = r_в s_y/s_x (x – ) ,

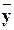
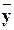
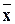
где s_x и s_y – выборочные средние квадратические отклонения X и Y , а

r_в = –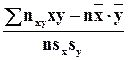

выборочный коэффициент корреляции, вычисленный по сгруппированным данным. Здесь n_xy – частота пары вариант (x,y). Аналогично находят выборочное уравнение прямой линии регрессии X на Y :

_y – = r_в s_x/s_y (y – )

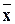
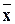
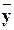
Для того, чтобы установить, соответствует ли найденная по выборке математическая модель зависимости между Y и X статистическим данным, следует оценить значимость коэффициентов регрессии и значимость уравнения регрессии.

Проверить значимость коэффициентов регрессии означает установить, достаточна ли величина оценки для обоснованного вывода о том, что коэффициент регрессии отличен от нуля. Выдвигают гипотезу H₀ : коэффициент регрессии равен нулю β =0. Проверку гипотезы H₀ осуществляют с помощью распределенной по закону Стьюдента статистики

t = │b / s_b│

где b – оценка коэффициента регрессии, а s_b – оценка его среднего квадратического отклонения, другими словами стандартная ошибка оценки. Если │t │≥ t_кр ( α, k ), нулевую гипотезу о равенстве нулю коэффициента регрессии отвергают, и коэффициент считают значимым. При │t │

b – t(α,k)s_b 2 – коэффициент детерминации, n – объем выборки, k – количество факторных признаков.