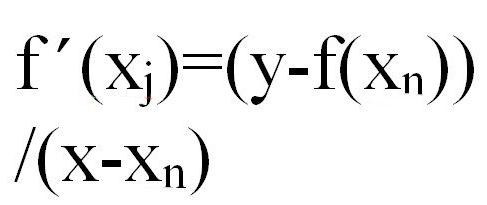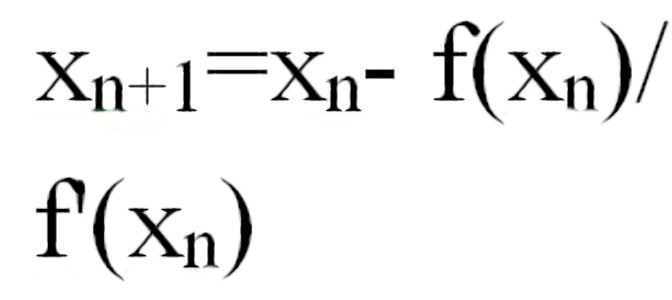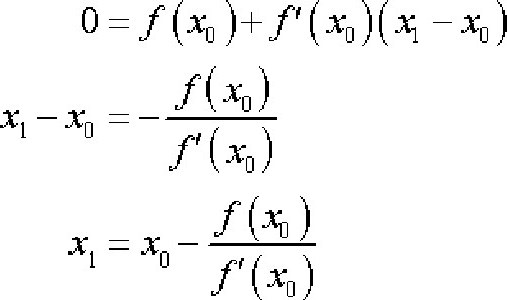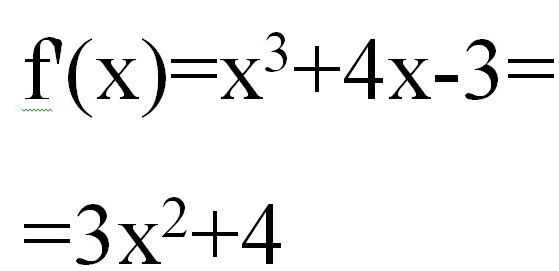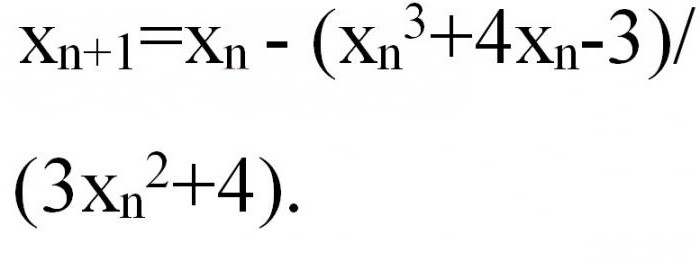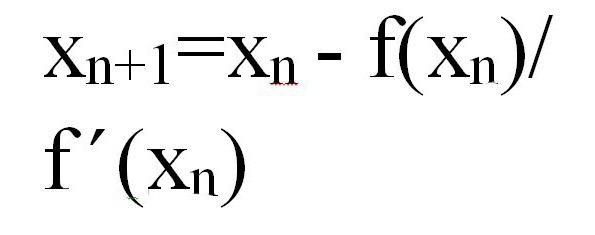Вычисление корня уравнения методом касательных

Метод Ньютона

Инструкция . Введите выражение F(x) , нажмите Далее . Полученное решение сохраняется в файле Word . Также создается шаблон решения в Excel .

• Решение онлайн
• Видеоинструкция
• Оформление Word

Правила ввода функции, заданной в явном виде

2. Примеры правильного написания F(x) :
   1. 10•x•e 2x = 10*x*exp(2*x)
   2. x•e -x +cos(3x) = x*exp(-x)+cos(3*x)
   3. x 3 -x 2 +3 = x^3-x^2+3
   4. Выражение 0.9*x=sin(x)+1 необходимо преобразовать к виду: sin(x)+1-0.9*x . Аналогично, x^2-7=5-3x к виду x^2+3x-12 .

   Пусть дано уравнение f(x)=0 , где f(x) определено и непрерывно в некотором конечном или бесконечном интервале a ≤ x ≤ b . Всякое значение ξ, обращающее функцию f(x) в нуль, то есть такое, что f(ξ)=0 называется корнем уравнения или нулем функции f(x) . Число ξ называется корнем k -ой кратности, если при x = ξ вместе с функцией f(x) обращаются в нуль ее производные до (k-1) порядка включительно: f(ξ)=f’(ξ)= … =f k-1 (ξ) = 0 . Однократный корень называется простым.
   Приближенное нахождение корней уравнения складывается из двух этапов:

   1. Отделение корней, то есть установление интервалов [α_i,β_i] , в которых содержится один корень уравнения.
      1. f(a)•f(b) , т.е. значения функции на его концах имеют противоположные знаки.
      2. f’(x) сохраняет постоянный знак, т.е. функция монотонна (эти два условия достаточны, но НЕ необходимы) для единственности корня на искомом отрезке).
      3. f”(x) сохраняет постоянный знак, т.е. функция выпукла вверх, либо – вниз.
   2. Уточнение приближенных корней, то есть доведение их до заданной точности.

   Геометрическая интерпретация метода Ньютона (метод касательных)

   Критерий завершения итерационного процесса имеет вид

   Метод Ньютона

   Этот онлайн калькулятор ищет корень (нуль) заданной функции, используя метод Ньютона (также известный как метод касательных)

   Этот онлайн калькулятор применяет метод Ньютона (также известный как метод касательных) используя калькулятор производных для получения аналитической формулы производной заданной функции (метод Ньютона требует вычисления производной). Под калькулятором можно прочитать краткое описание метода.

   

   Метод Ньютона

   Метод Ньютона 1

   Метод Ньютона, алгоритм Ньютона (также известный как метод касательных) — это итерационный численный метод нахождения корня (нуля) заданной функции. Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном (1643—1727). Поиск решения осуществляется путём построения последовательных приближений и основан на принципах простой итерации.

   Основная идея метода заключается в следующем: задаётся начальное приближение вблизи предположительного корня, после чего строится касательная к графику исследуемой функции в точке приближения, для которой находится пересечение с осью абсцисс. Эта точка берётся в качестве следующего приближения. Далее процесс повторяется, пока не будет достигнута необходимая точность.

   Уравнение касательной к графику функции выглядит следующим образом:
   ,
   где — тангенс угла пересечения касательной с осью абсцисс.

   Тангенс угла пересечения касательной с осью абсцисс, — не что иное, как значение производной в точке .
   С учетом того факта, что в точке пересечения с осью абсцисс значение y равно нулю, можно записать следующее выражение для нахождения точки пересечения (следующей точки приближения):

   Метод Ньютона является очень мощным методом поиска корней функции, так как имеет квадратичную скорость сходимости — количество значащих цифр примерно удваивается с каждым шагом итерации, однако существуют и ограничения, затрудняющие его применение. Так, например, если начальное приближение недостаточно близко к решению, то метод может не сойтись, если производная не непрерывна в точке корня, то метод может расходиться в любой окрестности корня, если не существует вторая производная в точке корня, то скорость сходимости метода может быть заметно снижена, если производная в точке корня равна нулю, то скорость сходимости не будет квадратичной, а сам метод может преждевременно прекратить поиск, и дать неверное для заданной точности приближение.

   Теорема Канторовича дает следующие условия применимости метода для поиска корней функции:

   1. функция должна быть ограничена;
   2. функция должна быть гладкой, дважды дифференцируемой;
   3. её первая производная f'(x) равномерно отделена от нуля;
   4. её вторая производная f»(x) должна быть равномерно ограничена.

   Метод касательных: описание

   Мучаясь в школе над решением уравнений на уроках математики, многие ученики часто уверены, что тратят время абсолютно впустую, а между тем такой навык пригодится в жизни не только тем, кто решит пойти по стопам Декарта, Эйлера или Лобачевского.

   На практике, например в медицине или экономике, сплошь и рядом встречаются ситуации, когда специалисту требуется выяснить, когда концентрация активного вещества того или иного препарата достигнет требуемого уровня в крови пациента или нужно высчитать время, необходимое конкретному бизнесу для того, чтобы он стал рентабельным.

   Чаще всего речь идет о решении нелинейных уравнений различного типа. Сделать это максимально быстро, особенно с использованием ЭВМ, позволяют численные методы. Они хорошо изучены и давно доказали свою эффективность. К их числу относится и метод касательных Ньютона, которым посвящена эта статья.

   

   Постановка задачи

   В данном случае имеется функция g, которая задана на отрезке (a, b) и принимает на нем определенные значения, т. е. каждому x, принадлежащему (a, b) возможно сопоставить конкретное число g(x).

   Требуется установить все корни уравнения из промежутка между точками a и b (включая концы), для которых функция обнуляется. Очевидно, что это будут точки пересечения y = g(x) с ОХ.

   В некоторых случаях удобнее заменить g(x)=0 на аналогичное, вида g₁(x) = g₂(x). В таком случае в качестве корней выступают абсциссы (значение x) точек пересечения графиков g₁(x) и g₂(x).

   Решение нелинейного уравнения важно и для задач оптимизации, для которых условие локального экстремума — обращение в 0 производной функции. Иными словами, такая задача может свестись к поиску корней уравнения p(x) = 0, где p(x) тождественна g'(x).

   Методы решения

   Для некоторых видов нелинейных уравнений, например квадратных или простых тригонометрических, найти корни можно достаточно простыми способами. В частности, каждый школьник знает формулы, используя которые можно без проблем находить значения аргумента точек, где обнуляется квадратный трехчлен.

   Способы извлечения корней нелинейных уравнений принято делить на аналитические (прямые) и итерационные. В первом случае искомое решение имеет вид формулы, используя которую за некоторое число арифметических операций можно найти значение искомых корней. Подобные методы разработаны для показательных, тригонометрических, логарифмических и простейших алгебраических уравнений. Для остальных же приходится использовать специальные численные методы. Их легко реализовать с помощью ЭВМ, которые позволяют найти корни с требуемой точностью.

   К их числу относится и так называемый численный метод касательных. Последний был предложен великим ученым Исааком Ньютоном в конце XVII века. В последующие столетия метод неоднократно совершенствовался.

   Локализация

   Численные способы решения сложных уравнений, не имеющих аналитических решений, принято осуществлять в 2 этапа. Сначала требуется их локализировать. Эта операция заключается в нахождение таких отрезков на ОХ, на которых существует один корень решаемого уравнения.

   Рассмотрим отрезок [a,b]. Если g(x) на нем не имеет разрывов и принимает в концевых точках значения разных знаков, то между a и b или в них самих расположен по крайней мере 1 корень уравнения g(x) = 0. Чтобы он был единственным, требуется, чтобы g(x) на [a,b] была монотонной. Как известно, таким свойством она будет обладать при условии знакопостоянства g’(x).

   Говоря иначе, если на [a,b] g(x) не имеет разрывов и монотонно растет или убывает, а ее значения в концевых точках имеют не одинаковые знаки, то на [a, b] существует 1 и только 1 корень g(x).

   При этом следует знать, что этот критерий не будет действовать для корней уравнений, являющихся кратными.

   Решение уравнения делением пополам

   Прежде чем рассматривать более сложные численные методы (метод касательных и его разновидности) стоит познакомиться с наиболее простым способом выявления корней. Он называется дихотомией и относится к интуитивным методам. Алгоритм нахождения корней основан на теореме о том, что если для g(x), непрерывной на [x₀, x₁] выполняется условие разнознаковости, то на рассматриваемом отрезке есть хотя бы 1 корень g(x) = 0.

   Для его обнаружения нужно поделить отрезок [x₀, x₁] пополам и обозначить среднюю точку как x₂. Тогда возможны два варианта: g(x₀) * g(x₂) либо g(x₂) * g(x₁) равны или меньше 0. Выбираем тот, для которого верно одно из этих неравенств. Повторяем процедуру, описанную выше, пока длина [x₀, x₁] не станет меньше некой, заранее выбранной величины, определяющей точность определения корня уравнения на [x₀, x₁].

   К достоинствам метода относится его надежность и простота, а недостаток — необходимость изначально выявить точки, в которых g(x) принимает разные знаки, поэтому его нельзя применять для корней, обладающих четной кратностью. Кроме того, он не обобщается на случай системы уравнений или если речь идет о комплексных корнях.

   Пример 1

   Пусть мы хотим решить уравнение g(x) = 2x 5 + x — 1 = 0. Чтобы долго не искать подходящий отрезок, строим график, используя, например, известную программу «Эксель». Мы видим, что в качестве отрезка для локализации корня лучше брать значения из промежутка [0,1]. Мы можем быть уверены, что хотя бы один корень искомого уравнения на нем есть.

   g'(x) = 10x 4 + 1, т. е. это монотонно возрастающая функция, поэтому на выбранном отрезке есть только 1 корень.

   Подставляем концевые точки в уравнение. Имеем 0 и 1 соответственно. На первом шаге за решение берем точку 0,5. Тогда g(0,5) = -0,4375. Значит ,следующий отрезок для деления пополам будет [0,5, 1]. Его серединная точка — 0,75. В ней значение функции равно 0,226. Берем для рассмотрения отрезок [0,5, 0,75] и его середину, которая находится в точке 0,625. Вычисляем значение g(x) в 0,625. Оно равно -0,11, т. е. отрицательное. Опираясь на этот результат, выбираем отрезок [0,625, 0,75]. Получаем x = 0,6875. Тогда g(x) = -0,00532. Если точность решения 0,01, то можем считать, что искомый результат равен 0,6875.

   Теоретическая база

   Этот способ нахождения корней методом касательных Ньютона пользуется популярностью из-за его очень быстрой сходимости.

   Он основан на том доказанном факте, что если x_n — приближение к корню f(x)=0, таком, что f’ C 1 , то следующая апроксимация будет в точке, где обнуляется уравнение касательной к f(x), т. е.

   

   Подставляем x = x_n+1 и обнуляем y.

   Тогда алгоритм метода касательных выглядит так:

   

   Пример 2

   Попробуем использовать классический метод касательных Ньютона и найти решение какого-либо нелинейного уравнения, которое сложно или невозможно отыскать аналитически.

   Пусть требуется выявить корни для x 3 + 4x — 3 = 0 с некоторой точностью, например 0,001. Как известно, график любой функции в виде многочлена нечетной степени должен хотя бы раз пересекать ось ОХ, т. е. сомневаться в существовании корней не приходится.

   Прежде чем решить наш пример методом касательных, строим график f(x) = x 3 + 4x — 3 поточечно. Это очень легко сделать, например, используя табличный процессор «Эксель». Из полученного графика будет видно, что на [0,1] происходит его пересечение с осью ОХ и функция y = x 3 + 4x — 3 монотонно возрастает. Мы можем быть уверены, что на [0,1] уравнения x 3 + 4x — 3 = 0 имеет решение и оно единственное.

   

   Алгоритм

   Любое решение уравнений методом касательных начинается с вычисления f ‘(x). Имеем:

   

   Тогда вторая производная будет иметь вид x * 6.

   Используя эти выражения, можем записать формулу для выявления корней уравнения по методу касательных в виде:

   

   Далее требуется выбрать начальное приближение, т. е. заняться определением, какую точку считать стартовой (об. x₀) для итерационного процесса_. Рассматриваем концы отрезка [0,1]. Нам подойдет тот, для которого верно условие разнознаковости функции и ее 2-ой производной в x₀. Как видим, при подстановке x₀ = 0 оно нарушено, а вот x₀ = 1 вполне подходит.

   

   то если нас интересует решение методом касательных с точностью e, то значение x_n можно считать удовлетворяющим требованиям задачи, при условии выполнения неравенства|f(x_n) / f’(x_n)| 3 + 4x₀ — 3) / (3x₀ 2 + 4) = 1- 0,2857 = 0,71429;

3. так как условие не выполняется, идем далее;
4. получаем новое значение для x₂, которое равно 0,674;
5. замечаем, что отношение значения функции к ее производной в x₂ меньше 0,0063, прекращаем процесс.



Метод касательных в Excel

Решить предыдущий пример можно намного легче и быстрее, если не производить расчеты вручную (на калькуляторе), а использовать возможности табличного процессора от компании «Майкрософт».

Для этого в «Эксель» нужно создать новую страницу и заполнить ее ячейки следующими формулами:

• в C7 записываем «= СТЕПЕНЬ (B7;3) + 4 * B7 — 3»;
• в D7 вписываем «= 4 + 3 * СТЕПЕНЬ (B7;2)»;
• в E7 записываем «= (СТЕПЕНЬ (B7;3)- 3 + 4 * B7) / (3* СТЕПЕНЬ (B7;2) + 4)»;
• в D7 вписываем выражение «=В7 – Е7»;
• в B8 вписываем формулу-условие «= ЕСЛИ(Е7 4 – 4 – 2 * х методом касательных в Паскале.

Используем вспомогательную функцию, которая поможет осуществить приближенное вычисление f'(x) = (f(x + delta) — f(x)) / delta. В качестве условия для завершения итерационного процесса выберем выполнение неравенства|x₀-x₁| 27 августа, 2017




источники:

http://planetcalc.ru/7748/

http://fb.ru/article/337323/metod-kasatelnyih-opisanie