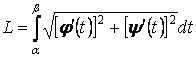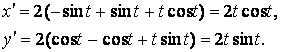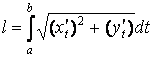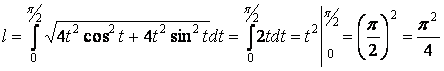Вычислить длины дуг линий заданных уравнениями

Калькулятор длины дуги кривой линии в декартовых координатах

Одним из приложений определенного интеграла является вычисление длины дуги плоской кривой. На рисунке изображен график функции :

Для того, чтобы узнать длину дуги кривой линии изображенной на рисунке, необходимо вычислить определенный интеграл:

В более общем случае, если у нас задана функция в декартовых координатах и стоит задача найти длину дуги этой кривой между точками и , нам необходимо вычислить интеграл:

В приведенной выше формуле, выражение означает, что сначала нужно вычислить производную функции , а затем полученное выражение возвести в квадрат.

Наш онлайн калькулятор, построенный на основе системы Wolfram Alpha, позволяет вычислить длину кривой, заданной в декартовых координатах для любой, даже очень сложной функции.

Вычислить длины дуг линий заданных уравнениями

&nbsp &nbsp &nbsp &nbsp Пусть кривая задана уравнениями в параметрической форме

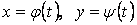
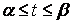
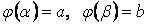
где &nbsp &nbsp &nbsp &nbsp и &nbsp &nbsp &nbsp &nbsp .
&nbsp &nbsp &nbsp &nbsp Длина дуги кривой

&nbsp &nbsp &nbsp &nbsp Прежде, чем Вы начнёте скачивать свои варианты, попробуйте найти интеграл по образцу, приведённому ниже для варианта 27.

&nbsp &nbsp &nbsp &nbsp Вариант 1 &nbsp &nbsp Вариант 2 &nbsp &nbsp Вариант 3 &nbsp &nbsp Вариант 4 &nbsp &nbsp Вариант 5 &nbsp &nbsp Вариант 6

&nbsp &nbsp &nbsp &nbsp Вариант 7 &nbsp &nbsp Вариант 8 &nbsp &nbsp Вариант 9 &nbsp &nbsp Вариант 10 &nbsp &nbsp Вариант 11 &nbsp &nbsp Вариант 12

&nbsp &nbsp Вариант 13 &nbsp &nbsp Вариант 14 &nbsp &nbsp Вариант 15 &nbsp &nbsp Вариант 16 &nbsp &nbsp Вариант 17 &nbsp &nbsp Вариант 18

&nbsp &nbsp Вариант 19 &nbsp &nbsp Вариант 20 &nbsp &nbsp Вариант 21 &nbsp &nbsp Вариант 22 &nbsp &nbsp Вариант 23 &nbsp &nbsp Вариант 24

&nbsp &nbsp Вариант 25 &nbsp &nbsp Вариант 26 &nbsp &nbsp Вариант 27 &nbsp &nbsp Вариант 28 &nbsp &nbsp Вариант 29 &nbsp &nbsp Вариант 30

&nbsp &nbsp &nbsp &nbsp Задача 18.27. Вычислить длину дуги кривой, заданной параметрическими уравнениями.

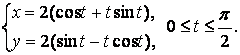
Решение

&nbsp &nbsp &nbsp &nbsp Найдём производные

&nbsp &nbsp &nbsp &nbsp Длина дуги кривой, заданной параметрически, ищется по формуле

&nbsp &nbsp &nbsp &nbsp Подставляя данные, получим

&nbsp &nbsp &nbsp &nbsp Ответ: &nbsp &nbsp &nbsp &nbsp .

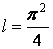
Как найти длину дуги кривой с помощью интеграла

Задачи на вычисление длины дуги кривой — однотипные. Существуют чёткие схемы для решения таких задач по формулам, которые отличаются в зависимости от того, какими и сколькими уравнениями задана кривая. Формулы представляют собой интегралы от корня, под которым в тех или иных сочетаниях присутствуют производные функций, которыми задана кривая. Следовательно, для того, чтобы вычислять длину дуги кривой, требуется уметь вычислять производные и интегралы. При вычислении интегралов возможны типичные трудности, связанные, например, с выбором подходящей подстановки. Эти задачи будем решать в примерах к данному уроку.

Вычисление длины дуги кривой, заданной в прямоугольных координатах

Пусть в прямоугольных координатах на плоскости уравнением y = f(x) задана кривая.

Найдём длину дуги AB этой кривой, заключённой между вертикальными прямыми x = a и x = b (рисунок ниже).

Возьмём на дуге AB точки A, M 1 , M 2 , . M i , . B с абсциссами x 0 = a, x 1 , x 2 , . x i , . b = x n и проведём хорды AM 1 , M 1 M 2 , . M n-1 B , длины которых обозначим соответственно через Δs 1 , Δs 2 , . Δs n . Тогда получим ломаную AM 1 M 2 . M n-1 B , вписанную в дугу AB. Длина ломаной равна

.

Длиной s дуги AB называется тот предел, к которому стремится длина вписанной ломаной, когда длина её наибольшего звена стремится к нулю:

.

Этот предел интегральной суммы равен определённому интегралу

(1).

Формула выше и есть формула для вычисления дуги кривой.

Пример 1. Найти длину дуги кривой , если .

Решение. Находим производную данной функции:

Используем формулу (1), подставляя найденную производную:

Ответ: длина дуги кривой равна 74.

Пример 2. Найти длину окружности .

Решение. Вычислим сначала длину четвёртой части окружности, лежащей в первом квадранте. Тогда уравнение дуги будет:

,

откуда находим производную функции:

Используем формулу (1) подставляя в неё производную, получаем:

Ответ: длина всей окружности равна .

Если в прямоугольных координатах уравнениями z = x(x) и y = y(x) задана пространственная кривая, то длина её дуги вычисляется по формуле:

. (2)

Вычисление длины дуги кривой, заданной параметрически

Найдём теперь длину дуги кривой в том случае, когда кривая задана параметрическими уравнениями:

В этом случае длину дуги кривой следует находить по формуле

(3).

Пример 3. Найти длину дуги кривой, заданной параметрическими уравнениями

если .

Решение. Рассчитаем интервал, в котором будет меняться значение t, если :

Вычислим производные функций x и y:

Используем формулу (3):

.

Ответ: длина дуги кривой равна 26.

Если параметрическими уравнениями

задана пространственная кривая, то длина её дуги вычисляется по формуле:

. (4)

Пример 4. Найти длину дуги винтовой линии, заданной параметрическими уравнениями

Решение. Вычислим производные функций x, y и z:

Используем формулу (4):

Вычисление длины дуги кривой, заданной в полярных координатах

Пусть кривая задана в полярных координатах:

Длина её дуги вычисляется по формуле:

(5).

Пример 5. Найти длину дуги кривой, заданной в полярных координатах .

Решение. Вычислим производную функции:

.

Заданная кривая — кардиоида (рисунок выше). Так как она симметрична, вычислим только ту часть длины дуги, у которой и и умножим её на 2. Используем формулу (5):

.