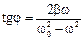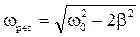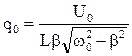Вынужденные электромагнитные колебания дифференциальное уравнение его решение

Вынужденные колебания

Определение вынужденных колебаний

Для того чтобы в реально существующей колебательной системе получать незатухающие колебания, следует каким-либо образом компенсировать потери энергии, которые происходят в результате существования сил сопротивления. Самым простым способом реализации незатухающих колебаний является воздействие на систему при помощи внешней периодической силы. Работа внешней силы обеспечить приток энергии в систему извне. Эта энергия не даст колебаниям затухнуть, при действии сил трения.

Колебания, которые возникают под действием периодически меняющейся силы (периодически изменяющейся ЭДС), называют вынужденными механическими (электромагнитными) колебаниями.

Дифференциальное уравнение вынужденных колебаний

Допустим, на механическую колебательную систему действует гармонически изменяющаяся внешняя сила:

Рассмотрим колебания груза на пружине (пружинный маятник). Уравнение незатухающих гармонических колебаний для этой системы можно записать как:

где $x$ — координата; $\delta $ — коэффициент затухания; $<\omega >_0$ — циклическая частота свободных незатухающих колебаний (если $\delta $=0, то $<\omega >_<0\ >$называют собственной частотой колебаний).

Если рассматривается, например, электрический колебательный контур, то роль периодически действующей силы может играть внешняя ЭДС или переменное напряжение. Их подводят к контуру извне и изменяются они по гармоническому закону. Уравнение колебаний в электрическом контуре можно представить как:

где $q$ — заряд; $\delta =\frac<2L>$ — коэффициент затухания; $<\omega >_0=\frac<1><\sqrt>$; $U=U_m<\cos \left(\omega t\right)\ >$ — внешнее переменное напряжение.

Уравнения (2) и (3) можно свести к линейному неоднородному дифференциальному уравнению вида:

где $s$ — колеблющийся параметр; $x_0=\frac$ если колебания механические ($x_0=\frac-\ в\ случае\ электрических\ колебаний$).

Решением уравнения (4) является сумма общего решения однородного уравнения и частного решения неоднородного уравнения. Однородное уравнение при этом имеет вид:

Его общее решение:

где $A_0$ — начальная амплитуда колебаний.

Частное решение уравнения (4) в представлено выражением:

Слагаемое $s_1$ в решении уравнения (5) играет значительную роль в начальной стадии установления колебаний, пока амплитуда вынужденных колебаний не будет определяться выражением (8).

Установившись, вынужденные колебания происходят с частотой $\omega $ и являются гармоническими. Амплитуда и фаза этих колебаний определяются равенствами (8) и (9), и они зависят от частоты $\omega $.

Резонанс вынужденных колебаний

Если частота вынуждающей силы приближается к собственной частоте колебаний, то возникает резкое увеличение амплитуды колебаний. Такое явление называют резонансом.

Из выражения (8) видно, что амплитуда имеет максимум. Для нахождения резонансной частоты (частоты при которой $A=max$), следует найти максимум функции $A(\omega )$. Взяв производную $\frac$ и приравняв ее к нулю получим:

Равенство (10) справедливо при:

Получается, что резонансная частота ($<\omega >_r$) равна:

При $<\delta >^2\ll <\omega >^2_0$ резонансная частота совпадает с собственной частотой колебаний $<\omega >_0.$ Подставим вместо частоты правую часть выражения (11) в формулу (8), получим выражение для резонансной амплитуды вынужденных колебаний:

При небольшом затухании колебаний (если $<\delta >^2\ll <\omega >^2_0$) амплитуда при резонансе равна:

где $Q=\frac<<\omega >_0><2\delta >$ — добротность колебательной системы, величина, характеризующая резонансные свойства колебательной системы. С увеличением добротности увеличивается амплитуда резонанса.

Примеры задач с решением

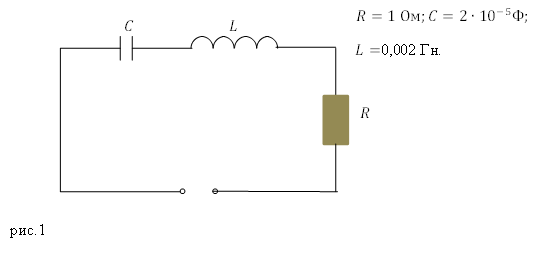
Задание. Какова добротность колебательного контура, представленного на рис.1?

Решение. Добротность электрического колебательного контура найдем как:

При этом собственная частота колебаний в таком контуре равна:

коэффициент затухания находим как:

Подставляет правые части выражений (1.2) (1.3) вместо соответствующих величин в (1.1), в результате, добротность представленного на рис. 1 контура найдем при помощи формулы:

Ответ. $Q=10$

Задание. Пружинный маятник выполняет вынужденные колебания в вязком веществе. Масса груза на пружине равна $m$, коэффициент упругости пружины $k$. Коэффициент сопротивления среды равен $r$. Систему заставляет совершать колебания сила $F=<\cos \left(\omega t\right)(Н).\ \ \ >$Чему равна резонансная амплитуда заданных колебаний ($A_r$)?

Решение. Допустим, что груз совершает колебания вдоль прямой X, тогда уравнением данных механических колебаний будет выражение:

где коэффициент затухания равен $\delta =\frac<2m>$. Из функции, которая задает вынуждающую силу:

мы видим, что амплитуда силы равна единице:

Собственная частота колебаний груза на пружине:

Амплитуда при резонансе таких колебаний равна:

Вынужденные электромагнитные колебания. Электромагнитные колебания в контуре — источник радиоволн

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На применении электромагнитных колебаний основана работа электромоторов, электрические лампы в наших квартирах и на улице, холодильник и пылесос работают, используя энергию электромагнитных колебаний. Электромагнитные колебания лежат в основе работы всей электронной аппаратуры, работающей с информацией, принимая, передавая или обрабатывая ее. Это связь, теле- и радиовещание, Интернет, поэтому важно изучить механизм протекания колебаний. Тема нашего урока связана с вынужденными электромагнитными колебаниями, сегодня мы рассмотрим электромагнитное поле и электромагнитные колебания в контуре.

Дифференциальное уравнение электромагнитных вынужденных колебаний и его решение. Резонанс

Электромагн вынужденные колебания:

Для того чтобы колеб в конт были не затух – подключим к нему послед-го источник синусоидального напряжения.

q’’+2βq’+ω 2 q=U₀cosωt/L-диф ур-ие вынужд элмагн колеб. Решение: q=q₀cos(ωt+φ)

Фазовое соотношение напряжений

U_c=q/c=q₀/c*cos(ωt-φ)=U_0c cos(ωt-φ), где U_0c= q₀/c-амплитудное значение напряж.на обклад. конденсатора изменяется в одной фазе.

Резонанс-резкое возрастание амплитуды вынужденных колебаний при приближении собственной частоты вынуждающей силы к собственной чатоте колебаний.

52.Волновой процесс: механизм образования механических волн в упругой среде. Уравнение плоской и сферической волн. Волновое уравнение.

Если в каком-либо месте упругой (жидкой, твердой или газообразной) среды возбудить колебания ее частиц, то вследствие взаимодействия между частицами это колебание может распространяться в среде от частицы к частице с некоторой скоростью 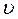. Процесс распространения колебаний в пространстве называется волной или волновым движением.

Направление распространения волны (колебания) называется лучом. Волна называется поперечной, если частицы среды колеблются перпендикулярно к лучу. Если же они колеблются вдоль луча, то волна называется продольной.

Продольные волны могут возникать в среде, облапдающей упругостью объема, т.е. в твердых, жидких и газообразных телах. Поперечные волны возникают только в среде, обладающей упругостью формы, т.е. только в твердых телах. Исключение составляет волны на поверхности воды ( и вообще на поверхности раздела сред, имееющих разную плотность), где упругость формы обеспечивается силами тяжести и поверхностного натяжения.

Распространяясь от источника колебаний, волновой процесс охватывает все новые и новые части пространства. Фронт волны представляет собой ту поверхность, которая отделяет часть пространства, уже вовлеченную в волновой процесс, от области, в которой колебания еще не возникли.

Геометрическое место точек, колеблющихся в одной фазе, называется волновой поверхностью. Волновые поверхности остаются неподвижными. Волновой фронт все время перемещается.

Волновые поверхности могут быть любой формы. В простейших случаях они имеют форму плоскости или сферы. Соответственно волна в этих случаях называется плоской или сферической.

Выведем уравнение плоской волны. Его называют еще уравнением бегущей волны.

Поперечная волна распространяется по оси ОХ (Рис.17.5) от источника гармонических колебаний с частотой . В точку С на расстоянии Х колебание придет через время , ( — скорость вдоль оси), тогда колебания

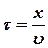
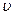
частицы в этой точке опишутся уравнение

Для опис-я волнового проц в среде треб найти ампл и фазу колеб разл точек среды и изм-я их по времени. Ур-ем волны назыв матем выр-ие которое задает смещения точек среды как ф-ию их коор. ξ(x,t)=0 Рассм одномерн синусоид плоскую волну распр вдоль оси Х. х=0; ξ(0;t)=acos(ωt); среда не погл a=const, за время τ→x=Vτ;

x→ξ(x,t)=acos[ω(t-τ)+φ]; ξ(x,t)=asin[ω(t-x/V)+φ]; с учетом ω=2π/T; VT=λ; 2π/λ=k;

ξ(x,t)=asin(ωt-kx+φ)-ур-е плоской одномерн волны. Где к-назыв волн числом, оно пок-т сколько длин волн λ откладыв на отрезке 2π метров.

Рассм сфер волну: в проц распр сфер волны за равные пром-и времени в колеб движ вовлек частицы среды в возр-х объемах ω↓; a↓; ξ(r,t)=Acos(ωt-kr+φ)/r – справедл при усл r>>d (d-диам ист-а сфер волн).

Ур-ие плоск волны явл-я реш-м диф ур-ия назыв-го волновым уравн: ξ(x,t)=Acos(ωt-kx- +φ0);