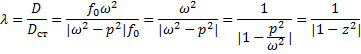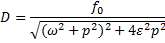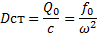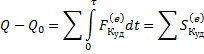Вынужденные колебания с одной степенью свободы уравнение

Вынужденные колебания системы с одной степенью свободы

Вынужденные колебания совершает механическая система, на которую наряду с упругими силами действуют периодически изменяющиеся силы, называемые возмущающими силами.

Пусть на одно из тел системы действует возмущающая сила, изменяющаяся по гармоническому закону

(1.27)

где F_o— амплитуда силы, р— частота, δ— начальная фаза.

Дифференциальное уравнение вынужденных колебаний системы с одной степенью свободы с учетом сил сопротивления имеет вид [1,2,3]:

, (1.28)

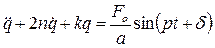
где .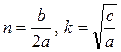

Из этого уравнения легко получить дифференциальное уравнение вынужденных колебаний системы с одной степенью свободы без учета сопротивления, положив в (1.28) n=0 , получаем:

(1.29)

Общее решение неоднородного дифференциального уравнения (1.28)

Можно найти как сумму двух решений: решения однородного дифференциального уравнения (1.11) и частного решения данного неоднородного дифференциального уравнения (1.28).

Решение однородного дифференциального уравнения (1.11) подробно рассмотрено в предыдущем параграфе.

Вид частного решения определяется видом правой части дифференциального уравнения (1.28).

Рассмотрим случай, когда закон изменения возмущающей силы имеет вид:

(1.30)

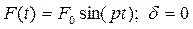
Для нашего случая частное решение ищем в виде:

(1.31)

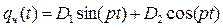
Подставляя (1.31) в (1.28) с учетом (1.30), после несложных преобразований, получаем:

(1.32)

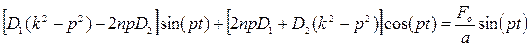
Сравнивая коэффициенты при соответствующих тригонометрических функциях справа и слева, получаем систему алгебраических уравнений для определения постоянных D₁ и D₂:

(1.33)

Решая эту систему, получаем следующие выражения для коэффициентов D₁ и D₂:

(1.34)

Таким образом, частное решение (1.31) определено.

Складывая теперь частное решение с решением однородного дифференциального уравнения (1.11), получаем уравнение движения системы, совершающей вынужденные колебания в среде с сопротивлением:

(1.35)

Вид решения однородного уравнения зависит от степени действующего на систему сопротивления среды.

Так, для случая малого сопротивления (n

(1.36)

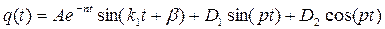
Постоянные А и β определяются из начальных условий q(0)=q₀ и .

Для этого найдем еще производную по времени от q(t) (1.36):

(1.37)

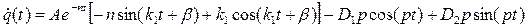
Подставляя начальные условия в (1.36) и (1.37) получаем систему алгебраических уравнений:

Решая эту систему, получаем:

(1.38)

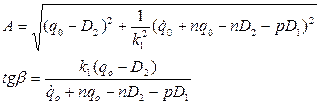
Таким образом, константы D₁, D₂, A, β в уравнении (1.36) определены, и следовательно получен закон вынужденных колебаний механической системы с одной степенью свободы для случая малого сопротивления (n k) общее решение уравнения (1.28) будет

(1.39)

А для случая достаточно большого сопротивления (n=k) ,будем иметь:

(1.40)

Константы А₁ и γ в уравнении (1.39) и С₁ и С₂ в уравнении (1.40) определяются по начальным условиям движения q₀ и 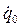. Процедура определения констант описана выше для случая малого сопротивления.

2.КУРСОВАЯ РАБОТА «ИССЛЕДОВАНИЕ ДВИЖЕНИЯ МЕХАНИЧЕСКОЙ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ ПРИ НАЛИЧИИ УПРУГИХ СВЯЗЕЙ»

Целью курсовой работы является приобретение навыков получения математической модели описывающей движение механической системы с одной степенью свободы с упругими связями путем составления дифференциального уравнения движения с помощью основных теорем и принципов теоретической механики и его дальнейшего решения аналитическим методом, а также проведение последующего численного анализа динамического поведения механической системы.

Вынужденные колебания с одной степенью свободы уравнение

1) Вынужденные колебания в системе с одной степенью свободы. Исследование коэффициента динамичности.

Колебательное движение механической системы — такое движени, при котором все ее обобщенные координаты или хотя бы одна из них изменяется с неоднократным возрастанием и убыванием.

Вынужденные колебания в системе с одной степенью свободы.

Вынужденные колебания — колебания, возникающие под влиянием внешнего воздействия на тела и точки механической системы.

Дифференциальное уравнение вынужденных колебаний линейной системы с одной степенью свободы:

, где a>0; b0; c>0.

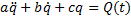
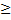
а — обобщенный коэффициент инерции; b — обобщенный коэффициент сопротивления; с — обобщенный коэффициент жесткости; Q(t) — обобщенная сила.

В случае, когда обобщенная сила Q(t), характеризующая внешнее воздействие на колебательную систему, изменяется во времени по закону синуса или косинуса:

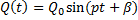
где Q₀ — амплитуда обобщенной силы; p — частота обобщенной силы; 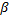— начальная фаза обобщенной силы, имеет место гармоническое возбуждение колебаний.

Амплитуда — наибольшее отклонение какой либо точки тела, совершающего колебания, от положения равновесия.

Частота — физическая величина, характеристика периодического процесса, равная числу полных циклов, совершённых за единицу времени, или проще: число периодов за одну секунду.

Фаза колебаний — физическая величина, при заданной амплитуде и коэффициенте затухания, определяющая состояние колебательной системы в любой момент времени, или проще: аргумент синуса.

Гармонические колебания — колебания, при которых обобщенная координата изменяется во времени по закону синуса или косинуса.

Исследование коэффициента динамичности.

λ — коэффициент динамичности, т.е. отношение амплитуды установившихся вынужденных колебаний к статическому смещению.

— коэффициент расстройки

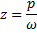
D — амплитуда вынужденных колебаний.

f₀ = Q₀/a — амплитуда вынуждающего ускорения

p — частота вынужденных колебаний

— коэффициент затухания

— круговая или циклическая частота

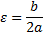
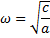
Dст — статическое смещение системы от положения равновесия под действием постоянной силы, равной амплитудному значению гармонического возмущающего воздействия.

Q₀ — амплитуда обобщенной возмущающей силы Q(t)

2) Удар точки о неподвижную поверхность. Коэффициент восстановления.

Удар — механическое явление при котором происходит конечное измменение скоростей точки системы за очень малый промежуток времени.

Удар точки о неподвижную поверхность.

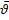
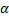
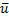
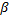
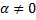
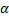
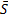
Материальная точка массы m падает на гладкую поверхность со скоростью , под углом (угол падения) к нормали (перпендикуляру) к поверхности (см. рисунок). После удара точка имеет скорость , направленную под углом (угол отражения) к нормали. Если , то удар точки о поверхность — косой, если =0 — прямой. Импульс ударной реакции поверхности направлен по нормали к поверхности.

Импульс силы (количество движения) — векторная физическая величина, являющаяся мерой действия силы за некоторый промежуток времени.

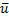
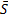
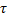
Для определения скорости точки после удара и импульса ударной реакции воспользуемся теоремой об изменении количества движения точки, в проекциях на нормаль n и касательную .

Теорема об изменении количества движения (при ударе):

Следовательно: ; .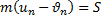

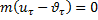
Отсюда: .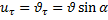

Для определения S и u_n необходимо знать коэффициент восстановления.

Коэффициент восстановления — отношение фазы восстановления к фазе деформирования, или отношение скорости после удара к скорости до удара.

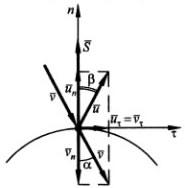
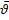
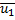
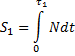
Для определения коэффициента восстановления представим удар точки о поверхность в двух фазах. В начале фазы деформирования скорость точки равна , в конце — . Импульс ударной реакции в этой фазе:

где 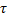1- время фазы деформирования; N — нормальная ударная реакции поверхности.

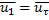
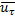
В конце фазы деформирования нормальная составляющая скорости точки равна нулю и (где — качательная составляющая скорости точки).

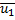
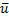
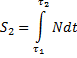
Фаза восстановления начинается при скорости точки и заканчивается, когда точка покидает поверхность со скоростью . Импульс ударной реакции в этой фазе:

Согласно теореме об изменении количества движения точки в проекции на нормаль для первой и второй фаз удара соответственно имеем:

; .

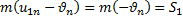
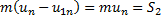
Заметим, что S₁ + S₂ = S. Разделив уравнение S₂ на S_1, получим уравнение для коэффициента восстановления:

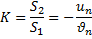
Коэффициент восстановления определяют экспериментально. Если K=1 удар называют абсолютно упругим и при K=0 — абсолютно неупругим, а при 0

Курсовая, реферат, контрольная – в чем же разница?

Вынужденные колебания систем с одной степенью свободы

К вынужденным колебаниям приводит непрерывное воздействие на механическую систему внешней периодической силы, например, изменяющейся по гармоническому закону

, (7.4.1)

где Р0 – амплитуда, т.е. максимальное значение возмущающей силы, W – круговая частота ее изменения.

Амплитуда вынужденных колебаний системы Авын рассчитывается по формуле

(7.4.2)

где yst – перемещение y системы, которое вызвало бы статическое приложение максимального значения Р0 возмущающей силы;

(7.4.3)

– коэффициент нарастания колебаний (без затухания).

В расчетах на прочность систем, совершающих вынужденные колебания, используют динамический коэффициент kd , определяемый по формуле

(7.4.4)

где – статическое перемещение y системы, вызванное ее собственным весом Р = mg.

С учетом закона Гука условие прочности для системы, совершающей вынужденные колебания, записывается следующим образом

(7.4.5)

Здесь – статическое напряжение, вызванное собственным весом системы.

Задача 7.4.1. На двух двутавровых балках № 12 посередине установлен двигатель весом Q = 7 кН (рис. 7.4.1). Неуравновешенные массы двигателя условно заменены вра-щающимся со скоростью

грузом Q2 = 120 Н, радиус вращения которого R = 0,21 м.

Проверить прочность балок, приняв их длину l = 1,6 м, модуль упругости материала балок Е = 2·105 МПа, расчетное сопротивление стали изгибу, растяжению по пределу текучести Ry = 220 МПа.

Коэффициент условий работы балок g с = 1 (табл.1.1).

Решение. 1. Выписываем из сортамента (таблица III, a приложения) геометрические характеристики поперечного сечения двутавровой балки и устанавливаем вес Q1 одной балки: момент инерции Iz = 350 см4, момент сопротивления Wz = 58,4 см3, масса 1 м двутавра № 12 q = 11,5 кг/м. Масса одной балки m1 = ql = 11,5·1,6 = 18,4 кг; вес Q1 одной балки

В дальнейшем расчет проводится для одной балки (из двух).

2. Рассчитаем собственную круговую частоту колебаний w системы, для чего воспользуемся формулой (7.3.5)

где yst – прогиб посередине балки, вызванный весом Q /2 и весом балки Q1.

Следует учесть, что при расчете собственной частоты балки, как системы с одной степенью свободы, в расчет вводится приведенная масса

Для балки на двух опорах коэффициент привидения a = 17/35 » 0,5.

При расчете yst можно использовать известную в теории изгиба балок формулу

(7.4.6)

которая в данной задаче принимает вид

Таким образом, частота собственных колебаний системы равна

3. Рассчитаем максимальное напряжение s st в среднем сечении балки, нагруженной статически приложенными силами Q /2 и Q1 = qlg,

4. Рассчитаем коэффициент нарастания колебаний b по формуле (7.4.3), установив предварительно величину частоты Ω возмущающей силы

5. Рассчитаем динамический коэффициент kd, используя формулу (7.4.4).

Для этого по известным из теории изгиба балок формулам определим прогибы: yst(Q2) – прогиб посередине балки, от статической сосредоточенной силы Р0, равной силе инерции груза Q2 /2

т.е., применяя формулу (7.4.6), находим

yst(Q,Q1) = yst(Q) + yst(Q1) – прогиб посередине балки, нагруженной статической сосредоточенной силой Q /2 и равномерно распределенной нагрузкой q = Q1 / l