Вынужденные колебания уравнение вынужденных колебаний и его решение

Вынужденные колебания. Резонанс. Автоколебания

Если колебания совершаются под воздействием внешней силы, они называются вынужденными. Работа внешней силы, которая обеспечивает колебательную систему энергией, при этом является положительной. Благодаря ей колебания не затухают и могут противодействовать силам трения.

Внешняя сила не обязательно должна быть постоянной. С течением времени она может изменяться по разным законам. Особый случай – воздействие на колебательную систему внешней силы, которая изменяется по гармоническому закону с частотой, равной ω , в то время как сама система совершает собственные колебания с той же самой частотой.

Установившиеся вынужденные колебания всегда происходят с частотой внешней силы. Частоту свободных колебаний определяют параметры системы.

Когда внешняя сила начинает воздействовать на колебательную систему, должно пройти некоторое время Δ t , прежде чем вынужденные колебания установятся. Это время будет равно тому времени τ , за которое затухают свободные колебания в данной системе.

В момент начала воздействия в системе начинают происходить два процесса одновременно – свободные колебания с собственной частотой ω 0 и вынужденные с частотой ω . Однако из-за сил трения свободные колебания в определенный момент затухают, поэтому по прошествии времени в системе сохраняются лишь стационарные колебания с той частотой, которая соответствует внешней (вынуждающей) силе.

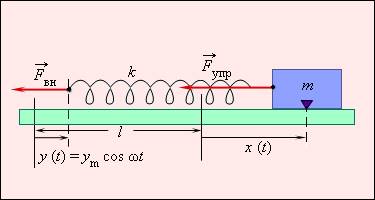
Разберем пример. У нас есть тело на пружине, совершающее вынужденные колебания (см. иллюстрацию ниже). Приложим внешнюю силу, обозначенную F → в н , к свободному концу пружины, после чего этот конец начнет перемещаться по закону, выражаемому формулой:

Здесь буквой ω обозначена круговая частота, а y m – амплитуда колебаний.

Перемещения такого рода обеспечиваются шатунным механизмом, который преобразует круговые движения в возвратно-поступательные.

Рисунок 2 . 5 . 1 . Груз на пружине, совершающий вынужденные колебания. Перемещение свободного конца выражено формулой y = y m cos ω t , где l означает длину недеформированной пружины, а k –ее жесткость.

При смещении левого конца пружины на некоторое расстояние y и правого – на x по сравнению с первоначальным положением недеформированной пружины будет происходить ее удлинение. Найти величину этого удлинения можно по следующей формуле:

∆ l = x — y = x — y m cos ω t .

В таком случае мы можем переформулировать второй закон Ньютона для этого случая следующим образом:

m a = — k ( x — y ) = — k x + k y m cos ω t .

Здесь сила, которая действует на тело, показана как сумма двух слагаемых, первым из которых является упругость, стремящаяся к равновесию тела, а вторым – внешнее воздействие, совершающееся с определенными интервалами. Внешнюю силу также называют вынуждающей.

Теперь выразим эту зависимость в строгой математической формуле, учитывающей связь между координатой тела a = x ¨ и его ускорением. У нас получится следующее:

x ¨ + ω 0 2 x = A cos ω t .

Эта зависимость называется уравнением внешних колебаний. Здесь ω 0 = k m является собственной круговой частотой свободного колебания, а ω – циклической частотой внешней (вынуждающей) силы.

Чтобы найти величину A для вынужденного колебания груза на пружине, нужно воспользоваться следующей формулой:

A = k m y m — ω 0 2 y m .

То уравнение, что мы записали перед этим, не учитывает, что на тело действуют также и силы трения. В уравнении вынужденных колебаний, в отличие от уравнения свободных, учитываются сразу обе частоты – частота вынуждающей силы и частота свободных колебаний.

Вынужденные колебания груза на пружине, которые устанавливаются со временем, имеют частоту внешнего воздействия. Это определяется следующим законом:

x ( t ) = x m cos ( ω t + θ ) .

Здесь x m обозначает амплитуду вынужденного колебания, а буква θ – его начальную фазу. Значения обоих этих показателей будут зависеть от амплитуды внешней силы и соотношения частот.

Если частоты очень низкие, т.е. ω ≪ ω 0 , то тело, прикрепленное к правому концу пружины, движется точно так же, как и левый конец этой пружины. Тогда получается, что x ( t ) = y ( t ) . Сама пружина при этом практически не деформируется, а модуль внешней силы F → в н , приложенной к ее левому концу, стремится к нулю. Работа при этом не совершается.

Понятие резонанса

Резонанс – это резкое возрастание амплитуды вынужденных колебаний при сближении частоты внешней силы с собственной частотой колебания тела.

С помощью резонансной кривой (резонансной характеристики) можно описать зависимость, существующую между амплитудой внешних колебаний x m и частотой вынуждающей силы ω .

Когда происходит резонанс, амплитуда x m может оказаться значительно больше, чем амплитуда колебаний левого (свободного) конца пружины.. Если мы не будем учитывать силы трения, то получится, что при резонансной частоте амплитуда вынужденных колебаний будет возрастать неограниченно. В реальности она будет зависеть от следующего условия: работа внешней силы в течение всего времени колебаний должна совпадать с потерями механической энергии, происходящими из-за трения. При уменьшении трения (и, соответственно, повышении добротности Q колебательной системы) амплитуда вынужденных колебаний при резонансе возрастет.

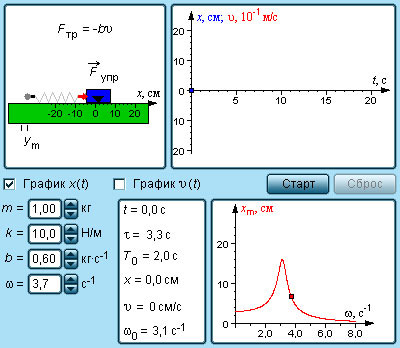
Рисунок 2 . 5 . 2 . Моделирование вынужденных колебаний.

Если добротность колебательной системы невысока (менее 10 ), то частота резонанса будет находиться ближе к низким частотам. Это показано на иллюстрации 2 . 5 . 2 .

Явление резонанса имеет большое практическое значение. Именно из-за него зачастую разрушаются здания, мосты и другие сооружения. Это происходит в тот момент, когда их собственные частоты совпадают с частотой внешней силы, например, колебаниями мотора.

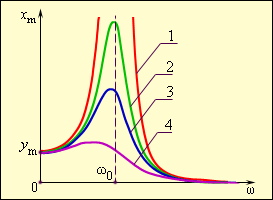
Рисунок 2 . 5 . 3 . Изображение затухания различных колебаний при помощи резонансных кривых: 1 — условная система без учета трения (бесконечное возрастание амплитуды вынужденных колебаний), 2 , 3 , 4 – резонансные колебания в реальных условиях, происходящих в системах разной степени добротности ( Q 2 > Q 3 > Q 4 ) . Если частоты низкие, то ( ω ≪ ω 0 ) x m ≈ y m , а если высокие, то ( ω ≫ ω 0 ) x m → 0 .

Вынужденные колебания являются незатухающими. При трении неизбежно теряется часть энергии, однако воздействие внешних периодически действующих сил компенсирует ее.

Что такое автоколебательные системы

Автоколебательные системы – это системы, в которых могут возникать незатухающие колебания безотносительно внешнего воздействия, а лишь за счет способности самостоятельно регулировать подвод энергии от внешнего источника. Процесс колебаний в таких системах называют автоколебаниями.

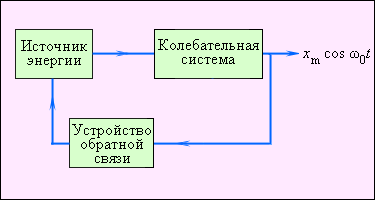
Внутри этой системы можно выделить три составляющих – саму систему, источник внешней постоянной энергии и обратную связь между ними. Первым элементом выступает любая механическая система, которая может совершать затухающие колебания, например, часовой маятник. В качестве источника можно использовать потенциальную энергию груза в поле тяжести или энергию деформации пружины. Система обратной связи – это, как правило, особый механизм, функцией которого является регулирование поступлений энергии. На иллюстрации показано, как эти компоненты взаимодействуют между собой.

Рисунок 2 . 5 . 4 . Автоколебательная система со всеми основными составляющими.

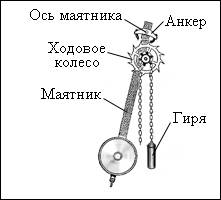
Какие можно привести примеры таких систем? Ярким примером является часовой механизм с так называемым анкерным ходом. В нем есть ходовое колесо с косыми зубчиками, прочно сцепленное с зубчатым барабаном, через который перекинута цепочка с грузом. В верхней части маятника закреплен якорек (анкер), состоящий из двух твердых пластинок, дугообразно изогнутых по окружности с центром на основной оси. В механизме ручных часов вместо гири используется пружина, а вместо маятника – маховичок-балансир, соединенный со спиральной пружиной, который совершает круговые колебания вокруг своей оси. В качестве источника внешней энергии выступает заведенная пружина или поднятая гиря. Обратная связь осуществляется с помощью анкера: он позволяет ходовому колесу совершать поворот только на один зубец за полупериод. Когда анкер взаимодействует с ходовым колесом, происходит передача энергии. Когда маятник колеблется, зубец ходового колеса передает анкерной вилке энергию по направлению движения маятника, и именно этим компенсируются силы трения. Таким образом, энергия поднятой гири или заведенной пружины поступает маленькими порциями к маятнику.

Существует также много других автоколебательных систем, которые широко применяются в технике. Автоколебания происходят внутри двигателей внутреннего сгорания, паровых машин, электрических звонков, музыкальных инструментов, голосовых связок и т.д.

Рисунок 2 . 5 . 5 . Схема маятникового часового механизма.

Вынужденные колебания

Определение вынужденных колебаний

Для того чтобы в реально существующей колебательной системе получать незатухающие колебания, следует каким-либо образом компенсировать потери энергии, которые происходят в результате существования сил сопротивления. Самым простым способом реализации незатухающих колебаний является воздействие на систему при помощи внешней периодической силы. Работа внешней силы обеспечить приток энергии в систему извне. Эта энергия не даст колебаниям затухнуть, при действии сил трения.

Колебания, которые возникают под действием периодически меняющейся силы (периодически изменяющейся ЭДС), называют вынужденными механическими (электромагнитными) колебаниями.

Дифференциальное уравнение вынужденных колебаний

Допустим, на механическую колебательную систему действует гармонически изменяющаяся внешняя сила:

Рассмотрим колебания груза на пружине (пружинный маятник). Уравнение незатухающих гармонических колебаний для этой системы можно записать как:

где $x$ — координата; $\delta $ — коэффициент затухания; $<\omega >_0$ — циклическая частота свободных незатухающих колебаний (если $\delta $=0, то $<\omega >_<0\ >$называют собственной частотой колебаний).

Если рассматривается, например, электрический колебательный контур, то роль периодически действующей силы может играть внешняя ЭДС или переменное напряжение. Их подводят к контуру извне и изменяются они по гармоническому закону. Уравнение колебаний в электрическом контуре можно представить как:

где $q$ — заряд; $\delta =\frac<2L>$ — коэффициент затухания; $<\omega >_0=\frac<1><\sqrt>$; $U=U_m<\cos \left(\omega t\right)\ >$ — внешнее переменное напряжение.

Уравнения (2) и (3) можно свести к линейному неоднородному дифференциальному уравнению вида:

где $s$ — колеблющийся параметр; $x_0=\frac$ если колебания механические ($x_0=\frac-\ в\ случае\ электрических\ колебаний$).

Решением уравнения (4) является сумма общего решения однородного уравнения и частного решения неоднородного уравнения. Однородное уравнение при этом имеет вид:

Его общее решение:

где $A_0$ — начальная амплитуда колебаний.

Частное решение уравнения (4) в представлено выражением:

Слагаемое $s_1$ в решении уравнения (5) играет значительную роль в начальной стадии установления колебаний, пока амплитуда вынужденных колебаний не будет определяться выражением (8).

Установившись, вынужденные колебания происходят с частотой $\omega $ и являются гармоническими. Амплитуда и фаза этих колебаний определяются равенствами (8) и (9), и они зависят от частоты $\omega $.

Резонанс вынужденных колебаний

Если частота вынуждающей силы приближается к собственной частоте колебаний, то возникает резкое увеличение амплитуды колебаний. Такое явление называют резонансом.

Из выражения (8) видно, что амплитуда имеет максимум. Для нахождения резонансной частоты (частоты при которой $A=max$), следует найти максимум функции $A(\omega )$. Взяв производную $\frac$ и приравняв ее к нулю получим:

Равенство (10) справедливо при:

Получается, что резонансная частота ($<\omega >_r$) равна:

При $<\delta >^2\ll <\omega >^2_0$ резонансная частота совпадает с собственной частотой колебаний $<\omega >_0.$ Подставим вместо частоты правую часть выражения (11) в формулу (8), получим выражение для резонансной амплитуды вынужденных колебаний:

При небольшом затухании колебаний (если $<\delta >^2\ll <\omega >^2_0$) амплитуда при резонансе равна:

где $Q=\frac<<\omega >_0><2\delta >$ — добротность колебательной системы, величина, характеризующая резонансные свойства колебательной системы. С увеличением добротности увеличивается амплитуда резонанса.

Примеры задач с решением

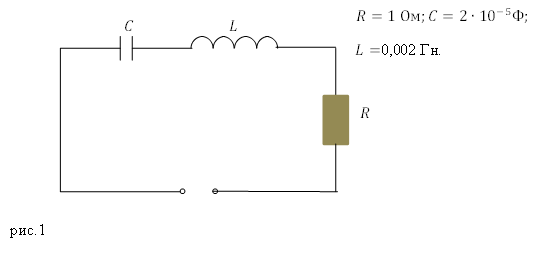
Задание. Какова добротность колебательного контура, представленного на рис.1?

Решение. Добротность электрического колебательного контура найдем как:

При этом собственная частота колебаний в таком контуре равна:

коэффициент затухания находим как:

Подставляет правые части выражений (1.2) (1.3) вместо соответствующих величин в (1.1), в результате, добротность представленного на рис. 1 контура найдем при помощи формулы:

Ответ. $Q=10$

Задание. Пружинный маятник выполняет вынужденные колебания в вязком веществе. Масса груза на пружине равна $m$, коэффициент упругости пружины $k$. Коэффициент сопротивления среды равен $r$. Систему заставляет совершать колебания сила $F=<\cos \left(\omega t\right)(Н).\ \ \ >$Чему равна резонансная амплитуда заданных колебаний ($A_r$)?

Решение. Допустим, что груз совершает колебания вдоль прямой X, тогда уравнением данных механических колебаний будет выражение:

где коэффициент затухания равен $\delta =\frac<2m>$. Из функции, которая задает вынуждающую силу:

мы видим, что амплитуда силы равна единице:

Собственная частота колебаний груза на пружине:

Амплитуда при резонансе таких колебаний равна:

Уравнение вынужденных колебаний

Если маятник отвести от положения устойчивого равновесия и отпустить, то он начнет совершать собственные затухающие колебания под действием упругой силы и силы сопротивления. Будем считать, что упругая сила пропорциональна смещению F_упр = −kx, а сила сопротивления пропорциональна скорости движения . Здесь и r – коэффициенты упругости и сопротивления. Если кроме этого приложить к маятнику еще внешнюю периодическую силу , то он будет совершать вынужденные колебания.

Получим формулу для амплитуды вынужденных колебаний маятника, решив уравнение второго закона Ньютона

. (16.1)

Разделив на массу, приведем уравнение к канонической форме

, (16.2)

Это дифференциальное уравнение вынужденных колебаний. В нем введены обозначения: – коэффициент затухания, – циклическая частота собственных свободных колебаний.

Как показывает опыт, если на маятник начать действовать периодической силой, то вынужденные колебания устанавливаются не сразу. В течение некоторого времени на вынужденные колебания накладываются собственные колебания. Но так как собственные колебания являются затухающими, то со временем они исчезают и маятник совершает только вынужденные колебания. Их частота равна частоте внешней периодической силы. Поэтому частное решение уравнения (16.2) будем искать для установившихся вынужденных колебаний в виде

, (16.3)

где – амплитуда колебаний, наибольшее смещение маятника от положения равновесия. Чтобы убедиться, что функция (16.3) является решением, следует подставить ее и первую, вторую производные в уравнение (16.2)

. (16.4)

Это уравнение содержит две неизвестные величины: амплитуду колебаний А и сдвиг фаз между силой и смещением . Для их определения воспользуемся заменой тригонометрического уравнения его геометрическим представлением в виде векторной диаграммы (рис. 16.1).

Для этого из полюса О следует провести векторы, длины которых равны амплитудам, а углы относительно полярной оси равны начальным фазам. Теперь, если вращать векторы вокруг полюса О против часовой стрелки с угловой скоростью, равной частоте ω, то их проекции будут равны членами уравнения (16.4).

На векторной диаграмме сумма векторов, изображающих слагаемые в левой части уравнения должна быть равна вектору, изображающему правую часть уравнения (16.4). Запишем теорему Пифагора для заштрихованного треугольник

. (16.5)

Отсюда получим уравнение для амплитуды вынужденных колебаний

. (16.6)

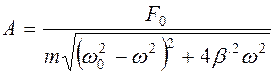
С ростом частоты амплитуда сначала возрастает от величины статического смещения , достигает наибольшего значения и затем снова уменьшается (рис. 16.2). Сильное увеличение амплитуды вынужденных колебаний при некоторой частоте называется резонансом. Чтобы получить условие резонанса, следует, как при поиске максимума функции, приравнять производную от подкоренного выражения (16.6) к нулю. Откуда получим . Как видно, резонанс наступает при частоте вынуждающей силы, близкой к частоте свободных колебаний. Подставив частоту резонансав формулу (16.6), получим для амплитуды резонанса

. (16.7)

Резонанс обусловлен тем, что направление скорости тела и направление силы совпадают в течение всего периода колебания. Поэтому отбор мощности от источника (N=F∙V)оказывается наибольший. Чем меньше сопротивление среды (β → 0), тем выше амплитуда при резонансе.

По резонансной кривой можно определить коэффициент затухания. Проведем на уровне горизонтальную линию (рис. 16.2). Абсциссы точек пересечения определим, подставив в левую часть уравнения (16.6) амплитуду при резонансе (16.7), деленную на . Решив квадратное уравнение относительно корней ω₁ и ω₂, получим, что полуширина резонансной кривой Δω = ω₁– ω₂ равна коэффициенту затухания: .

Сдвиг фаз между силой и смещением можно определить из треугольника векторной диаграммы (рис. 16.1)

. (16.8)

При малых частотах вынуждающей силы (ω

Определим центробежную силу инерции. Якорь – не болванка, а сложная конструкция и изготовить ее идеально точно крайне затруднительно. Центр масс якоря может быть смещен относительно оси вала на некоторое расстояние r₀. Уменьшают этот разбаланс методом статической балансировки, добиваясь при строго горизонтальной оси якоря безразличного равновесия в любом положении. Однако, возможно, что у одной части якоря ее центр масс находится по одну сторону оси вала, а у другой – по другую, хотя общий может быть на оси. Тогда при вращении возникает переменный момент сил. Его устраняют методом динамической балансировки, уравновешивая каждую часть якоря дополнительными грузами.

Ограничимся действием только центробежной силы инерции. Ее равнодействующая приложена к центру масс. Величина центробежной силы равна 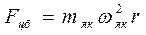, где m_як – масса якоря, ω_як – угловая скорость вращения якоря, r – расстояние от оси вращения до центра масс якоря. Вектор силы вращается вместе с якорем. В проекции на вертикальное направление, вдоль которого происходят колебания двигателя, центробежная сила становится периодической силой, вызывающей вынужденные колебания двигателя с циклической частотой, равной скорости вращения якоря:

. (16.9)

Амплитуда колебаний двигателя относительно вагона рассчитывается по формуле (6), при подстановке амплитуды центробежной силы

. (16.10)

Проблема в приведенных расчетах заключается в том, что вал при вращении под действием центробежной силы изгибается, и расстояние от оси вращения до центра масс r не постоянно, оно зависит от скорости вращения. При малой скорости вращения центробежная сила увеличивает изгиб вала. Если частота вращения оказывается равна частоте собственных колебаний якоря на валу, наступает резонанс и расстояние центра масс от оси вращения наибольшее. А при очень большой скорости вращения сила и смещение оказываются в противофазе, как это должно быть при вынужденных колебаниях якоря на валу, и смещение стремится к нулю. Вибрации при этом почти исчезают.

Таким образом, тяговый электродвигатель может иметь даже две резонансных частоты: при колебаниях двигателя как целого в подвеске и при колебаниях якоря относительно корпуса двигателя. Если же резонанс наступил, то следует быстрее увеличить скорость вращения и пройти опасный диапазон.

Задачи

1. Определить, при какой скорости вагон начнет сильно раскачиваться в вертикальном направлении из-за ударов о стыки рельсов. Масса вагона 60 т, коэффициент упругости восьми пружин подвески 2·10 7 Н/м, длина рельса 25 м.

2. Центр масс ротора массой 400 кг тягового двигателя массой 800 кг смещен относительно оси вращения на 0,01 мм. Двигатель подвешен к раме вагона, коэффициент упругости подвески 8·10 5 Н/м. При какой частоте вращения наступит резонанс. Определить амплитуду колебаний при резонансе, если коэффициент затухания амортизаторов 0,8 1/с.

3. Определить амплитуду вынуждающей силы вибростенда по графику зависимости амплитуды от частоты вынужденных колебаний (рис.16.4) колесной пары массой 1200 кг, установленной с пружинами подвески на вибростенде. Коэффициент затухания колебаний 0,3 1/с

4. Колесная пара массой 1300 кг с подвеской установлена на вибростенде. Определить приближенно по графику (рис.16.4) коэффициент затухания амортизаторов как полуширину резонансного пика на уровне . Определить коэффициент упругости пружин подвески.

5. На вагон массой 40 т со стороны рельсов действует вертикальная переменная сила F = 300 sin 31,4 t Н. При каком значении коэффициента упругости подвески вагона наступит резонанс. Чему равна при этом амплитуда колебаний, если коэффициент затухания 0,4 1/с.

6. Определить, при какой скорости начнет сильно раскачиваться вагон, совершая галопирующие колебания из-за ударов о стыки рельсов. Масса вагона 60 т, расстояние между осями 12 м, длина вагона 15м, коэффициент упругости передней и задней подвесок 1·10 7 Н/м. Длина рельса 25 м.

7. Определить, при какой амплитуде колебаний вагона при вибрации с частотой 20 Гц незакрепленные предметы будут подпрыгивать относительно пола вагона.

17. ВОЛНЫ В УПРУГИХ СРЕДАХ

Волны – это процесс распространения колебаний в пространстве. Существует большое многообразие видов механических волн в упругих средах. Наиболее известны объемные волны. В объеме газа, жидких и твердых сред могут распространяться продольные волны, в которых частицы совершают колебания вдоль направления распространения волны. В твердых средах могут распространяться поперечные волны, в которых частицы совершают колебания перпендикулярно направлению распространения волны. Различные виды волн распространяются вдоль поверхности жидкости, твердых тел, по земной коре. Распространяются волны в стержнях, шнурах, проводах и так далее. Всегда, когда среда обладает упругостью и массой, в ней могут распространяться упругие волны.

Уравнение волны.

Получим уравнение волны. Это уравнение изменения параметра колебаний частиц средыв любой точке пространства в зависимости от времени и расстояния до источника колебаний. Параметром, который периодически изменяется в упругой волне, может быть смещение частиц от положения равновесия, скорость частиц, или плотность и давление в жидкости и газе, механические напряжения, т.д. Под частицей понимается сравнительно небольшой объем вещества, но содержащий огромное число молекул, которые движутся совместно.

Пусть, например, смещение источника происходят по уравнению 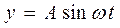, где А – амплитуда колебаний, ω – циклическая частота колебаний. Источник действует на ближайшие частицы окружающей среды, вынуждая их совершать колебания около их положений равновесия с частотой колебаний источника. Те, в свою очередь, заставляют совершать колебания следующие частицы. Происходит процесс распространения вынужденных колебаний в пространстве, который называется волной.

Поверхность среды, до которой дошло возбуждение от источника колебаний, называется фронтом волны. Форма фронта волны может быть различной. В однородной среде фронт от точечного источника (пульсирующий шарик) является сферическим. Фронт можно считать плоским на большом расстоянии от точечного источника или при излучении большой колеблющейся плоскостью, или при колебаниях поршня в цилиндрической трубе.

Пусть от источника распространяется вдоль оси x волна с плоским фронтом. Если можно пренебречь затуханием колебаний, то амплитуда колебаний частиц среды одинакова. Частицы среды начинают колебания позже, чем источник. Время запаздывания равно времени распространения волны , где V – скорость распространения фронта волны, x – расстояние от источника колебаний до частиц на фронте. Уравнение вынужденных колебаний частиц на оси x будет отличаться от уравнения колебаний источника только временем запаздывания

. (17.1)

Это уравнение является уравнением бегущей гармонической (синусоидальной) волны. Его можно изобразить графиком синусоиды, который вместе с волной перемещается вдоль оси x со скоростью фронта (рис. 17.1). За время одного периода колебаний фронт перемещается на расстояние, называемое длиной волны . Длина волны также равна расстоянию между ближайшими точками на линии распространения, разность фаз которых равна 2π радиан.

Перепишем уравнение волны, введя в него длину волны. Подставив при , получим

. (17.2)

Здесь называется волновым вектором. В общем случае это вектор, показывающий направление распространения фронта волны. Если волна распространяется в направлении против оси x, то волновой вектор в уравнении (17.2) отрицателен.

Функция (17.2) описывает распространение монохроматической бесконечной волны. Аргумент функции называется фазой. Поверхность среды, для частиц которой фаза постоянна, , называется волновой поверхностью. Для частиц на фронте фаза равна нулю. Фронт и волновые поверхности перемещаются с так называемой фазовой скоростью. Продифференцировав формулу фазы, получим .

Если волна излучается конечное время, то её описывают как группу монохроматических волн разных близких частот и скорость перемещения группы называют групповой скоростью.

При распространении волны частицы вещества, то есть масса вещества, волной не переносится. Переносится кинетическая и потенциальная энергия колебаний и импульс вследствие взаимодействия частиц.

Интерференция волн

Интерференция – это явление наложения волн, в результате которого в пространстве возникают области усиления и ослабления колебаний. Согласно принципу суперпозиции, волны при встрече не искажают друг друга, проходят друг через друга, не изменяясь. В области наложения волн происходит перераспределение энергии колебаний. Устойчивое во времени и в пространстве интерференционное распределение энергии возможно только при наложении когерентных волн. Волны являются когерентными, если разность фаз в точке наблюдения постоянна по времени и частоты одинаковы. Для поперечных волн дополнительно должно соблюдаться условие параллельности направления колебаний. Усиление колебаний будет, если в точке наблюдения разность фаз равна четному числу π радиан, (горб на горб). Волны ослабляют друг друга, если разность фаз равна нечетному числу π радиан, (горб на впадину).

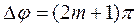
Рассмотрим частный случай интерференции – образование стоячих волн. Например, в струне, концы которой закреплены в стенках. Если перпендикулярно струне действует периодическая сила, то от места возбуждения в обоих направлениях распространяются поперечные волны. Достигнув места закрепления у стенки, волны отражаются. По закону сохранения энергии амплитуда отраженной волны должна быть равна амплитуде бегущей волны. Отраженная и бегущая волны интерферируют. Около самой стенки струна закреплена, и её конец совершать колебания не может. Значит, в этой точке отраженная волна должна быть в противофазе с бегущей волной. Уравнения для бегущей и отраженной волны примут вид

;(17.3)

. (17.4)

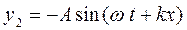
Здесь А – амплитуда колебаний w – циклическая частота, x– координата от начала струны. Бегущая и отраженная волны накладываются. Сложив уравнения волн по формулам тригонометрии, получим уравнение для результата интерференции

. (17.5)

Как видно, частицы струны совершают колебания с частотой бегущей волны, но фазовая скорость отсутствует. Собственно говоря, это не волна, а колебательное состояние среды. Его называют стоячей волной. Выражение имеет смысл амплитуды. Точки среды, где амплитуда равна нулю, называются узлами смещения. Расстояние между двумя соседними узлами равно половине длины волны. Узлы отделяют друг от друга изолированные зоны, называемые пучностями, в которых частицы совершают колебания (рис.17.2). Направления колебаний в соседних пучностях противоположны. Максимальная амплитуда в два раза больше амплитуды бегущих волн. Стоячая волна в струне может возникнуть при условии, что на её закрепленных концах будут узлы смещения. Для этого длина струны должна быть равна целому числу полуволн (рис.17.3).