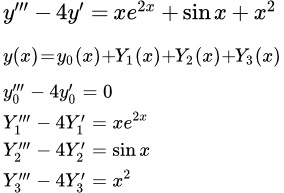Выполните решение неоднородного уравнения 1 степени

(-1) + ; (-1) + , n

+ n; + 2n, n

arctg(-2) + n; arctg + n, n

+ ≤ x ≤ + , n

+ ≤ x ≤ + , n

По окончанию самостоятельной работы учащиеся меняются тетрадями и проводят взаимопроверку. Правильные ответы заранее записаны учителем на закрытой доске.

III. Формирование новых знаний и понятий

Слова учителя: Теперь мы переходим к новой теме нашего занятия – решению неоднородных тригонометрических уравнений I степени.

Дается определение: Уравнение вида a sin x + b cos x = c, где а, b, с не равны 0, называется неоднородным тригонометрическим уравнением I степени.

Данное уравнение может быть решено тремя способами.

Первый способ – универсальная подстановка

sin x =

cos x =

Второй способ – введение дополнительного угла

a sinx + b cosx = sin(x+), где = arctg если a + b c, то уравнение имеет корни

Третий способ – переход к функциям половинного аргумента

sin x = 2 sin cos

cos x = cos — sin

IV. Применение знаний, навыков, понятий

Задания на отработку применения разобранных способов решения неоднородных тригонометрических уравнений. Решаются у доски учениками с помощью учителя:

1) sin 2x + cos 2x = sin 3x (через введение дополнительного угла)

sin (2x + ) = sin 3x sin (2x + ) = sin 3x sin (2x + ) — sin 3x = 0 2 sin cos = 0
sin () = 0 sin ( — ) = 0 x = + 2n, где n	или	cos () = 0 cos ( + ) = 0 x = + , где n

2) 3 sin x – 4 cos x = 5 (применение универсальной подстановки)

3 — 4 = 5
6 tg — 4 (1 — tg) = 5 (1 + tg)
(tg — 3) = 0
x = 2 arctg3 + 2n, где n

3) cos x – sin x = 1 (через переход к функциям половинного аргумента)

cos — sin — 2 sincos = sin + cos 2 sin(sin + cos) = 0
sin = 0 x = 2n	или	sin + cos = 0 – однородное первой степени tg = -1 x = — + 2n

Для самостоятельной работы учащихся (перед началом указываются способы решения):

1) sin x + cos x = (через введение дополнительного угла)

sin (x + ) =
sin (x + ) = 1
x = + 2n, где n

2) 3 sin x + 5 cos x= 6 (универсальная подстановка)

3 + 5 = 6
6 tg +5 — 5 tg = 6 + 6 tg
11 tg — 6 tg + 1= 0
решений нет, так как D 11.06.2011

Линейные неоднородные дифференциальные уравнения первого порядка

В данной теме поговорим о способах решения линейных неоднородных дифференциальных уравнений вида y ‘ = P ( x ) · y = Q ( x ) . Начнем с метода вариации произвольной постоянной и покажем способ применения этого метода для решения задачи Коши. Продолжим рассмотрением метода, который предполагает представление произвольной постоянной у как произведения двух функций u ( x ) и v ( x ) . В разделе мы приводим большое количество задач по теме с детальным разбором решения.

На тот случай, если применяемые при разборе темы термины и понятия окажутся незнакомыми для вас, мы рекомендуем заглядывать в раздел «Основные термины и определения теории дифференциальных уравнений».

Метод вариации произвольной постоянной для решения ЛНДУ первого порядка

Для краткости будет обозначать линейное неоднородное дифференциальное уравнение аббревиатурой ЛНДУ, а линейное однородное дифференциальное уравнение (ЛОДУ).

ЛНДУ вида y ‘ = P ( x ) · y = Q ( x ) соответствует ЛОДУ вида y ‘ = P ( x ) · y = 0 , при Q ( x ) = 0 . Если посмотреть на дифференциальное уравнение y ‘ = P ( x ) · y = 0 , становится понятно, что мы имеем дело с уравнением с разделяющимися переменными. Мы можем его проинтегрировать: y ‘ = P ( x ) · y = 0 ⇔ d y y = — P ( x ) d x , y ≠ 0 ∫ d y y = — ∫ P ( x ) d x ⇔ ln y + C 1 = — ∫ P ( x ) d x ⇔ ln y = ln C — ∫ P ( x ) d x , ln C = — C 1 , C ≠ 0 ⇔ e ln y = e ln C — ∫ P ( x ) d x ⇔ y = C · e — ∫ P ( x ) d x

Мы можем утверждать, что значение переменной y = 0 тоже является решением, так как при этом значении переменной уравнение y ‘ = P ( x ) · y = 0 обращается в тождество. Этому случаю соответствует решение y = C · e — ∫ P ( x ) d x при значении C = 0 .

Получается, что y = C · e — ∫ P ( x ) d x — общее решение ЛОДУ, где С – произвольная постоянная.

y = C · e — ∫ P ( x ) d x — это решение ЛОДУ y ‘ = P ( x ) · y = 0 .

Для того, чтобы найти общее решение неоднородного уравнения y ‘ = P ( x ) · y = Q ( x ) , будем считать С не константой, а функцией аргумента х . Фактически, мы примем y = C ( x ) · e — ∫ P ( x ) d x общим решением ЛНДУ.

Подставим y = C ( x ) · e — ∫ P ( x ) d x в дифференциальное уравнение y ‘ = P ( x ) · y = Q ( x ) . Оно при этом обращается в тождество:

y ‘ = P ( x ) · y = Q ( x ) C x · e — ∫ P ( x ) d x + P ( x ) · C ( x ) · e — ∫ P ( x ) d x = Q ( x )

Теперь обратимся к правилу дифференцирования произведения. Получаем:

C ‘ ( x ) · e — ∫ P ( x ) d x + C ( x ) · e — ∫ P ( x ) d x + P ( x ) · C ( x ) · e — ∫ P ( x ) d x = Q ( x )

Производная сложной функции e — ∫ P ( x ) d x ‘ равна e — ∫ P ( x ) d x · — ∫ P ( x ) d x ‘ .

Теперь вспомним свойства неопределенного интеграла. Получаем:

e — ∫ P ( x ) d x · — ∫ P ( x ) d x ‘ = — e — ∫ P ( x ) d x · P ( x )

Теперь выполним переход:

C ‘ ( x ) · e — ∫ P ( x ) d x + C ( x ) · e — ∫ P ( x ) d x ‘ + P ( x ) · C ( x ) · e — ∫ P ( x ) d x = Q ( x ) C ‘ ( x ) · e — ∫ P ( x ) d x — P ( x ) · C ( x ) · e — ∫ P ( x ) d x + P ( x ) · C ( x ) · e — ∫ P ( x ) d x = Q ( x ) C ‘ ( x ) · e — ∫ P ( x ) d x = Q ( x )

Так мы пришли к простейшему дифференциальному уравнению первого порядка. В ходе решения этого уравнения мы определим функцию C ( x ) . Это позволит нам записать решение исходного ЛНДУ первого порядка следующим образом:

y = C ( x ) · e — ∫ P ( x ) d x

Подведем итог

Метод вариации произвольной постоянной при решении ЛНДУ предполагает проведение трех этапов:

• нахождение общего решения соответствующего ЛОДУ y ‘ + P ( x ) · y = 0 в виде y = C · e — ∫ P ( x ) d x ;
• варьирование произвольной постоянной С , что заключается в замене ее функцией С ( x ) ;
• подстановка функции y = C ( x ) · e — ∫ P ( x ) d x в исходное дифференциальное уравнение, откуда мы можем вычислить C ( x ) и записать ответ.

Теперь применим этот алгоритм к решению задачи.

Найдите решение задачи Коши y ‘ — 2 x y 1 + x 2 = 1 + x 2 , y ( 1 ) = 3 .

Нам нужно отыскать частное решение ЛНДУ y ‘ — 2 x y 1 + x 2 = 1 + x 2 при начальном условии y ( 1 ) = 3 .

В нашем примере P ( x ) = — 2 x 1 + x 2 и Q ( x ) = x 2 + 1 . Начнем с того, что найдем общее решение ЛОДУ. После этого применим метод вариации произвольной постоянной и определим общее решение ЛНДУ. Это позволит нам найти искомое частное решение.

Общим решением соответствующего ЛОДУ y ‘ — 2 x y 1 + x 2 = 0 будет семейство функций y = C · ( x 2 + 1 ) , где С – произвольная постоянная.

Варьируем произвольную постоянную y = C ( x ) · ( x 2 + 1 ) и подставляем эту функцию в исходное уравнение:
y ‘ — 2 x y 1 + x 2 = 1 + x 2 C x · ( x 2 + 1 ‘ — 2 x · C ( x ) · ( x 2 + 1 ) 1 + x 2 = 1 + x 2 C ‘ ( x ) · ( x 2 + 1 ) + C ( x ) · 2 x — 2 x · C ( x ) = 1 + x 2 C ‘ ( x ) = 1 ,

откуда C ( x ) = ∫ d x = x + C 1 , где C 1 – произвольная постоянная.

Это значит, что y = C ( x ) · ( x 2 + 1 ) = ( x + C 1 ) · ( x 2 + 1 ) — общее решение неоднородного уравнения.

Теперь приступим к отысканию частного решения, которое будет удовлетворять начальному условию y ( 1 ) = 3 .

Так как y = ( x + C 1 ) · ( x 2 + 1 ) , то y ( 1 ) = ( 1 + C 1 ) · ( 1 2 + 1 ) = 2 · ( 1 + C 1 ) . Обратившись к начальному условию, получаем уравнение 2 · ( 1 + C 1 ) = 3 , откуда C 1 = 1 2 . Следовательно, искомое решение задачи Коши имеет вид y = x + 1 2 · ( x 2 + 1 )

Теперь рассмотрим еще один метод решения линейных неоднородных дифференциальных уравнений y ‘ + P ( x ) · y = Q ( x ) .

Еще один метод решения ЛНДУ первого порядка

Мы можем представить неизвестную функцию как произведение y = u ⋅ v , где u и v – функции аргумента x .

Мы можем подставить эту функцию в ЛНДУ первого порядка. Имеем:

y ‘ + P ( x ) · y = Q ( x ) ( u · v ) ‘ + P ( x ) · u · v = Q ( x ) u ‘ · v + u · v ‘ + P ( x ) · u · v = Q ( x ) u ‘ · v + u · ( v ‘ + P ( x ) · v ) = Q ( x )

Если найти такое v , чтобы оно было ненулевым частным решением дифференциального уравнения v ‘ + P ( x ) · v = 0 , то u можно будет определить из уравнения с разделяющимися переменными u ‘ · v = Q ( x ) .

Рассмотрим этот алгоритм решения на предыдущем примере. Это позволит нам сосредоточиться на главном, не отвлекаясь на второстепенные детали.

Найдите общее решение линейного неоднородного дифференциального уравнения y ‘ — 2 x y 1 + x 2 = 1 + x 2 .

Пусть y = u ⋅ v , тогда
y ‘ — 2 x y x 2 + 1 = x 2 + 1 ⇔ ( u · v ) — 2 x · u · v x 2 + 1 = x 2 + 1 u ‘ · v + u · v ‘ — 2 x · u · v x 2 + 1 = x 2 + 1 u ‘ · v + u · v ‘ — 2 x · v x 2 + 1 = x 2 + 1

Находим такое v , отличное от нуля, чтобы выражение в скобках обращалось в ноль. Иными словами, находим частное решение дифференциального уравнения v ‘ — 2 x · v x 2 + 1 = 0 .
v ‘ — 2 x · v x 2 + 1 = 0 ⇔ d v d x = 2 x · v x 2 + 1 ⇒ d v v = 2 x d x x 2 + 1 ⇔ d v v = d ( x 2 + 1 ) x 2 + 1 ∫ d v v = ∫ d ( x 2 + 1 ) x 2 + 1 ln v + C 1 = ln ( x 2 + 1 ) + C 2

Возьмем частное решение v = x 2 + 1 , соответствующее C 2 – С 1 = 0 .

Для этого частного решения имеем
u ‘ · v + u · v ‘ — 2 x · v x 2 + 1 = x 2 + 1 ⇔ u ‘ · ( x 2 + 1 ) + u · 0 = x 2 + 1 ⇔ u ‘ = 1 ⇔ u = x + C

Следовательно, общее решение исходного линейного неоднородного дифференциального уравнения есть y = u · v = ( x + C ) · ( x 2 + 1 )

Ответы в обоих случаях совпадают. Это значит, что оба метода решения, которые мы привели в статье, равнозначны. Выбирать, какой из них применить для решения задачи, вам.

Пример решения линейного дифференциального уравнения с постоянными коэффициентами со специальной неоднородной частью

Здесь мы рассмотрим пример решения линейного дифференциального уравнения со специальной неоднородной частью. Метод решения таких уравнений подробно рассмотрен на странице «Решение линейных дифференциальных уравнений с постоянными коэффициентами со специальной неоднородной частью».

Пример

Общее решение однородного уравнения

Вначале находим общее решение однородного дифференциального уравнения
.
Ищем решение в виде . Составляем характеристическое уравнение:
.
Преобразуем его.
;
.
Получили три действительных корня:
.
Им соответствуют три решения фундаментальной системы решений:
.
Общее решение однородного уравнения:
.

Ищем частное решение неоднородного уравнения. Для этого неоднородную часть представим в виде суммы трех частей:
.

Частное решение с первой неоднородностью

Ищем частное решение дифференциального уравнения с первой неоднородной частью.
(П1) .
Неоднородность имеет вид многочлена первой степени, умноженного на экспоненту:
.
Характеристическое уравнение имеет корень , кратности . Тогда частное решение имеет вид многочлена первой степени, умноженного на и на экспоненту:
.
Находим производные.
;

;

;

.
Подставляем в (П1):

.
Сокращаем на и преобразуем:
.
Отсюда:

;
.

Частное решение со второй неоднородностью

Ищем частное решение со второй неоднородной частью:
(П2) .
Неоднородность имеет вид суммы произведений многочленов степени 0 (то есть постоянных), умноженных на косинус и синус:

.
Поскольку характеристическое уравнение не имеет комплексного корня , то частное решение имеет вид суммы произведений многочленов степеней 0 (то есть постоянных), умноженных на косинус и синус:
.
Находим производные.
;
;
;
.
Подставляем в (П2):
.
Преобразуем:
.
Отсюда

;
.

Частное решение с третьей неоднородностью

Ищем частное решение дифференциального уравнения с третьей неоднородной частью:
(П3) .
Здесь неоднородная часть является многочленом второй степени. Ему соответствует . Правую часть можно записать в стандартном виде так:
.
Поскольку характеристическое уравнение имеет однократный корень , то частное решение имеет вид многочлена второй степени, умноженного на (здесь p = 1 – кратность корня ):
.
Находим производные:
;
;
.
Подставляем в (П3):
.
Преобразуем:
.
Отсюда

;
.

Общее решение исходного уравнения:
.

Автор: Олег Одинцов . Опубликовано: 30-07-2013 Изменено: 15-10-2020