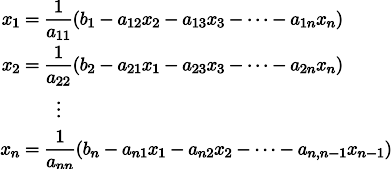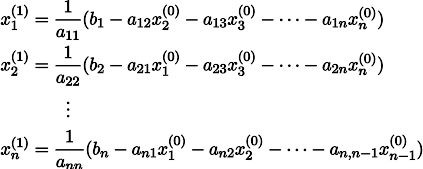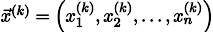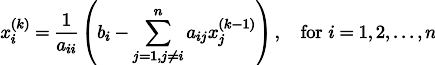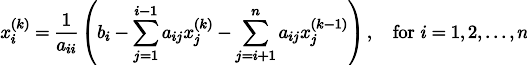Метод наименьших квадратов
Начнем статью сразу с примера. У нас есть некие экспериментальные данные о значениях двух переменных – x и y . Занесем их в таблицу.
| i = 1 | i = 2 | i = 3 | i = 4 | i = 5 | |
| x i | 0 | 1 | 2 | 4 | 5 |
| y i | 2 , 1 | 2 , 4 | 2 , 6 | 2 , 8 | 3 , 0 |
После выравнивания получим функцию следующего вида: g ( x ) = x + 1 3 + 1 .
Мы можем аппроксимировать эти данные с помощью линейной зависимости y = a x + b , вычислив соответствующие параметры. Для этого нам нужно будет применить так называемый метод наименьших квадратов. Также потребуется сделать чертеж, чтобы проверить, какая линия будет лучше выравнивать экспериментальные данные.
В чем именно заключается МНК (метод наименьших квадратов)
Главное, что нам нужно сделать, – это найти такие коэффициенты линейной зависимости, при которых значение функции двух переменных F ( a , b ) = ∑ i = 1 n ( y i — ( a x i + b ) ) 2 будет наименьшим. Иначе говоря, при определенных значениях a и b сумма квадратов отклонений представленных данных от получившейся прямой будет иметь минимальное значение. В этом и состоит смысл метода наименьших квадратов. Все, что нам надо сделать для решения примера – это найти экстремум функции двух переменных.
Как вывести формулы для вычисления коэффициентов
Для того чтобы вывести формулы для вычисления коэффициентов, нужно составить и решить систему уравнений с двумя переменными. Для этого мы вычисляем частные производные выражения F ( a , b ) = ∑ i = 1 n ( y i — ( a x i + b ) ) 2 по a и b и приравниваем их к 0 .
δ F ( a , b ) δ a = 0 δ F ( a , b ) δ b = 0 ⇔ — 2 ∑ i = 1 n ( y i — ( a x i + b ) ) x i = 0 — 2 ∑ i = 1 n ( y i — ( a x i + b ) ) = 0 ⇔ a ∑ i = 1 n x i 2 + b ∑ i = 1 n x i = ∑ i = 1 n x i y i a ∑ i = 1 n x i + ∑ i = 1 n b = ∑ i = 1 n y i ⇔ a ∑ i = 1 n x i 2 + b ∑ i = 1 n x i = ∑ i = 1 n x i y i a ∑ i = 1 n x i + n b = ∑ i = 1 n y i
Для решения системы уравнений можно использовать любые методы, например, подстановку или метод Крамера. В результате у нас должны получиться формулы, с помощью которых вычисляются коэффициенты по методу наименьших квадратов.
n ∑ i = 1 n x i y i — ∑ i = 1 n x i ∑ i = 1 n y i n ∑ i = 1 n — ∑ i = 1 n x i 2 b = ∑ i = 1 n y i — a ∑ i = 1 n x i n
Мы вычислили значения переменных, при который функция
F ( a , b ) = ∑ i = 1 n ( y i — ( a x i + b ) ) 2 примет минимальное значение. В третьем пункте мы докажем, почему оно является именно таким.
Это и есть применение метода наименьших квадратов на практике. Его формула, которая применяется для поиска параметра a , включает в себя ∑ i = 1 n x i , ∑ i = 1 n y i , ∑ i = 1 n x i y i , ∑ i = 1 n x i 2 , а также параметр
n – им обозначено количество экспериментальных данных. Советуем вам вычислять каждую сумму отдельно. Значение коэффициента b вычисляется сразу после a .
Обратимся вновь к исходному примеру.
Здесь у нас n равен пяти. Чтобы было удобнее вычислять нужные суммы, входящие в формулы коэффициентов, заполним таблицу.
| i = 1 | i = 2 | i = 3 | i = 4 | i = 5 | ∑ i = 1 5 | |
| x i | 0 | 1 | 2 | 4 | 5 | 12 |
| y i | 2 , 1 | 2 , 4 | 2 , 6 | 2 , 8 | 3 | 12 , 9 |
| x i y i | 0 | 2 , 4 | 5 , 2 | 11 , 2 | 15 | 33 , 8 |
| x i 2 | 0 | 1 | 4 | 16 | 25 | 46 |
Решение
Четвертая строка включает в себя данные, полученные при умножении значений из второй строки на значения третьей для каждого отдельного i . Пятая строка содержит данные из второй, возведенные в квадрат. В последнем столбце приводятся суммы значений отдельных строчек.
Воспользуемся методом наименьших квадратов, чтобы вычислить нужные нам коэффициенты a и b . Для этого подставим нужные значения из последнего столбца и подсчитаем суммы:
n ∑ i = 1 n x i y i — ∑ i = 1 n x i ∑ i = 1 n y i n ∑ i = 1 n — ∑ i = 1 n x i 2 b = ∑ i = 1 n y i — a ∑ i = 1 n x i n ⇒ a = 5 · 33 , 8 — 12 · 12 , 9 5 · 46 — 12 2 b = 12 , 9 — a · 12 5 ⇒ a ≈ 0 , 165 b ≈ 2 , 184
У нас получилось, что нужная аппроксимирующая прямая будет выглядеть как y = 0 , 165 x + 2 , 184 . Теперь нам надо определить, какая линия будет лучше аппроксимировать данные – g ( x ) = x + 1 3 + 1 или 0 , 165 x + 2 , 184 . Произведем оценку с помощью метода наименьших квадратов.
Чтобы вычислить погрешность, нам надо найти суммы квадратов отклонений данных от прямых σ 1 = ∑ i = 1 n ( y i — ( a x i + b i ) ) 2 и σ 2 = ∑ i = 1 n ( y i — g ( x i ) ) 2 , минимальное значение будет соответствовать более подходящей линии.
σ 1 = ∑ i = 1 n ( y i — ( a x i + b i ) ) 2 = = ∑ i = 1 5 ( y i — ( 0 , 165 x i + 2 , 184 ) ) 2 ≈ 0 , 019 σ 2 = ∑ i = 1 n ( y i — g ( x i ) ) 2 = = ∑ i = 1 5 ( y i — ( x i + 1 3 + 1 ) ) 2 ≈ 0 , 096
Ответ: поскольку σ 1 σ 2 , то прямой, наилучшим образом аппроксимирующей исходные данные, будет
y = 0 , 165 x + 2 , 184 .
Как изобразить МНК на графике функций
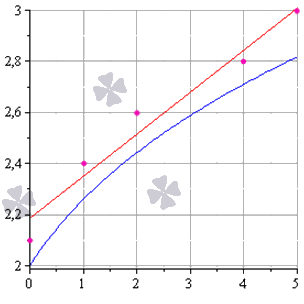
Метод наименьших квадратов наглядно показан на графической иллюстрации. С помощью красной линии отмечена прямая g ( x ) = x + 1 3 + 1 , синей – y = 0 , 165 x + 2 , 184 . Исходные данные обозначены розовыми точками.
Поясним, для чего именно нужны приближения подобного вида.
Они могут быть использованы в задачах, требующих сглаживания данных, а также в тех, где данные надо интерполировать или экстраполировать. Например, в задаче, разобранной выше, можно было бы найти значение наблюдаемой величины y при x = 3 или при x = 6 . Таким примерам мы посвятили отдельную статью.
Доказательство метода МНК
Чтобы функция приняла минимальное значение при вычисленных a и b , нужно, чтобы в данной точке матрица квадратичной формы дифференциала функции вида F ( a , b ) = ∑ i = 1 n ( y i — ( a x i + b ) ) 2 была положительно определенной. Покажем, как это должно выглядеть.
У нас есть дифференциал второго порядка следующего вида:
d 2 F ( a ; b ) = δ 2 F ( a ; b ) δ a 2 d 2 a + 2 δ 2 F ( a ; b ) δ a δ b d a d b + δ 2 F ( a ; b ) δ b 2 d 2 b
Решение
δ 2 F ( a ; b ) δ a 2 = δ δ F ( a ; b ) δ a δ a = = δ — 2 ∑ i = 1 n ( y i — ( a x i + b ) ) x i δ a = 2 ∑ i = 1 n ( x i ) 2 δ 2 F ( a ; b ) δ a δ b = δ δ F ( a ; b ) δ a δ b = = δ — 2 ∑ i = 1 n ( y i — ( a x i + b ) ) x i δ b = 2 ∑ i = 1 n x i δ 2 F ( a ; b ) δ b 2 = δ δ F ( a ; b ) δ b δ b = δ — 2 ∑ i = 1 n ( y i — ( a x i + b ) ) δ b = 2 ∑ i = 1 n ( 1 ) = 2 n
Иначе говоря, можно записать так: d 2 F ( a ; b ) = 2 ∑ i = 1 n ( x i ) 2 d 2 a + 2 · 2 ∑ x i i = 1 n d a d b + ( 2 n ) d 2 b .
Мы получили матрицу квадратичной формы вида M = 2 ∑ i = 1 n ( x i ) 2 2 ∑ i = 1 n x i 2 ∑ i = 1 n x i 2 n .
В этом случае значения отдельных элементов не будут меняться в зависимости от a и b . Является ли эта матрица положительно определенной? Чтобы ответить на этот вопрос, проверим, являются ли ее угловые миноры положительными.
Вычисляем угловой минор первого порядка: 2 ∑ i = 1 n ( x i ) 2 > 0 . Поскольку точки x i не совпадают, то неравенство является строгим. Будем иметь это в виду при дальнейших расчетах.
Вычисляем угловой минор второго порядка:
d e t ( M ) = 2 ∑ i = 1 n ( x i ) 2 2 ∑ i = 1 n x i 2 ∑ i = 1 n x i 2 n = 4 n ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2
После этого переходим к доказательству неравенства n ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2 > 0 с помощью математической индукции.
- Проверим, будет ли данное неравенство справедливым при произвольном n . Возьмем 2 и подсчитаем:
2 ∑ i = 1 2 ( x i ) 2 — ∑ i = 1 2 x i 2 = 2 x 1 2 + x 2 2 — x 1 + x 2 2 = = x 1 2 — 2 x 1 x 2 + x 2 2 = x 1 + x 2 2 > 0
У нас получилось верное равенство (если значения x 1 и x 2 не будут совпадать).
- Сделаем предположение, что данное неравенство будет верным для n , т.е. n ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2 > 0 – справедливо.
- Теперь докажем справедливость при n + 1 , т.е. что ( n + 1 ) ∑ i = 1 n + 1 ( x i ) 2 — ∑ i = 1 n + 1 x i 2 > 0 , если верно n ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2 > 0 .
( n + 1 ) ∑ i = 1 n + 1 ( x i ) 2 — ∑ i = 1 n + 1 x i 2 = = ( n + 1 ) ∑ i = 1 n ( x i ) 2 + x n + 1 2 — ∑ i = 1 n x i + x n + 1 2 = = n ∑ i = 1 n ( x i ) 2 + n · x n + 1 2 + ∑ i = 1 n ( x i ) 2 + x n + 1 2 — — ∑ i = 1 n x i 2 + 2 x n + 1 ∑ i = 1 n x i + x n + 1 2 = = ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2 + n · x n + 1 2 — x n + 1 ∑ i = 1 n x i + ∑ i = 1 n ( x i ) 2 = = ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2 + x n + 1 2 — 2 x n + 1 x 1 + x 1 2 + + x n + 1 2 — 2 x n + 1 x 2 + x 2 2 + . . . + x n + 1 2 — 2 x n + 1 x 1 + x n 2 = = n ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2 + + ( x n + 1 — x 1 ) 2 + ( x n + 1 — x 2 ) 2 + . . . + ( x n — 1 — x n ) 2 > 0
Выражение, заключенное в фигурные скобки, будет больше 0 (исходя из того, что мы предполагали в пункте 2 ), и остальные слагаемые будут больше 0 , поскольку все они являются квадратами чисел. Мы доказали неравенство.
Ответ: найденные a и b будут соответствовать наименьшему значению функции F ( a , b ) = ∑ i = 1 n ( y i — ( a x i + b ) ) 2 , значит, они являются искомыми параметрами метода наименьших квадратов (МНК).
Методы наименьших квадратов без слёз и боли
Итак, очередная статья из цикла «математика на пальцах». Сегодня мы продолжим разговор о методах наименьших квадратов, но на сей раз с точки зрения программиста. Это очередная статья в серии, но она стоит особняком, так как вообще не требует никаких знаний математики. Статья задумывалась как введение в теорию, поэтому из базовых навыков она требует умения включить компьютер и написать пять строк кода. Разумеется, на этой статье я не остановлюсь, и в ближайшее же время опубликую продолжение. Если сумею найти достаточно времени, то напишу книгу из этого материала. Целевая публика — программисты, так что хабр подходящее место для обкатки. Я в целом не люблю писать формулы, и я очень люблю учиться на примерах, мне кажется, что это очень важно — не просто смотреть на закорючки на школьной доске, но всё пробовать на зуб.
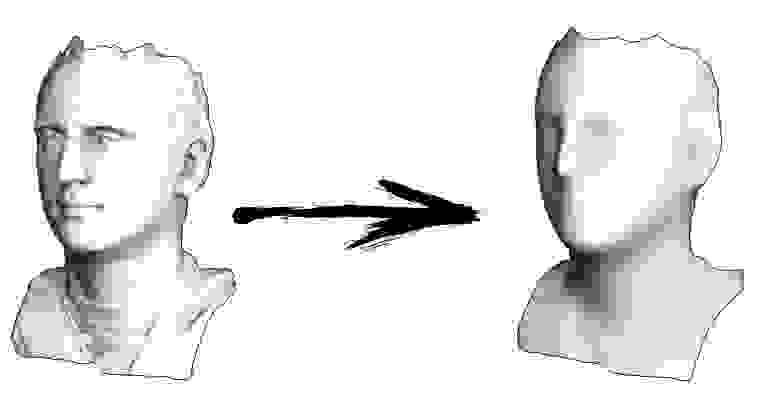
Итак, начнём. Давайте представим, что у меня есть триангулированная поверхность со сканом моего лица (на картинке слева). Что мне нужно сделать, чтобы усилить характерные черты, превратив эту поверхность в гротескную маску?
В данном конкретном случае я решаю эллиптическое дифференциальное уравнение, носящее имя Симеона Деми Пуассона. Товарищи программисты, давайте сыграем в игру: прикиньте, сколько строк в C++ коде, его решающем? Сторонние библиотеки вызывать нельзя, у нас в распоряжении только голый компилятор. Ответ под катом.
На самом деле, двадцати строк кода достаточно для солвера. Если считать со всем-всем, включая парсер файла 3Д модели, то в двести строк уложиться — раз плюнуть.
Пример 1: сглаживание данных
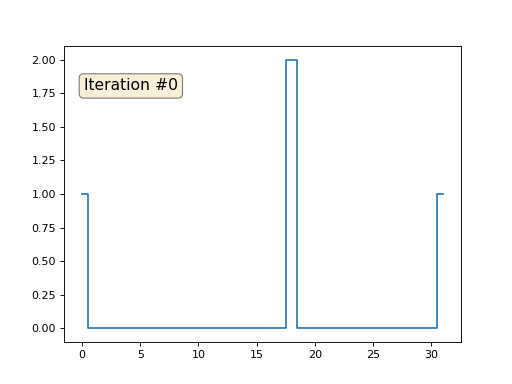
Давайте расскажу, как это работает. Начнём издалека, представьте, что у нас есть обычный массив f, например, из 32 элементов, инициализированный следующим образом:
А затем мы тысячу раз выполним следующую процедуру: для каждой ячейки f[i] мы запишем в неё среднее значение соседних ячеек: f[i] = ( f[i-1] + f[i+1] )/2. Чтобы было понятнее, вот полный код:
Каждая итерация будет сглаживать данные нашего массива, и через тысячу итераций мы получим постоянное значение во всех ячейках. Вот анимация первых ста пятидесяти итераций:
Если вам неясно, почему происходит сглаживание, прямо сейчас остановитесь, возьмите ручку и попробуйте порисовать примеры, иначе дальше читать не имеет смысла. Триангулированная поверхность ничем принципиально от этого примера не отличается. Представьте, что для каждой вершины мы найдём соседние с ней, посчитаем их центр масс, и передвинем нашу вершину в этот центр масс, и так десять раз. Результат будет вот таким:
Разумеется, если не остановиться на десяти итерациях, то через некоторое время вся поверхность сожмётся в одну точку ровно так же, как и в предыдущем примере весь массив стал заполнен одним и тем же значением.
Пример 2: усиление/ослабление характеристических черт
Полный код доступен на гитхабе, а здесь я приведу самую важную часть, опустив лишь чтение и запись 3Д моделей. Итак, триангулированная модель у меня представлена двумя массивами: verts и faces. Массив verts — это просто набор трёхмерных точек, они же вершины полигональной сетки. Массив faces — это набор треугольников (количество треугольников равно faces.size()), для каждого треугольника в массиве хранятся индексы из массива вершин. Формат данных и работу с ним я подробно описывал в своём курсе лекций по компьютерной графике. Есть ещё третий массив, который я пересчитываю из первых двух (точнее, только из массива faces) — vvadj. Это массив, который для каждой вершины (первый индекс двумерного массива) хранит индексы соседних с ней вершин (второй индекс).
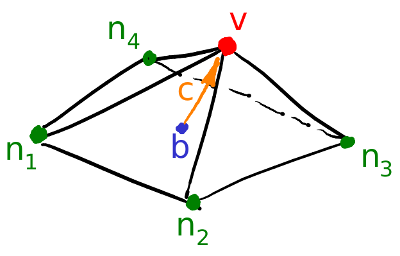
Первое, что я делаю, это для каждой вершины моей поверхности считаю вектор кривизны. Давайте проиллюстрируем: для текущей вершины v я перебираю всех её соседей n1-n4; затем я считаю их центр масс b = (n1+n2+n3+n4)/4. Ну и финальный вектор кривизны может быть посчитан как c=v-b, это не что иное, как обычные конечные разности для второй производной.
Непосредственно в коде это выглядит следующим образом:
Ну а дальше мы много раз делаем следующую вещь (смотрите предыдущую картинку): мы вершину v двигаем v := b + const * c. Обратите внимание, что если константа равна единице, то наша вершина никуда не сдвинется! Если константа равна нулю, то вершина заменяется на центр масс соседних вершин, что будет сглаживать нашу поверхность. Если константа больше единицы (заглавная картинка сделана при помощи const=2.1), то вершина будет сдвигаться в направлении вектора кривизны поверхности, усиливая детали. Вот так это выглядит в коде:
Кстати, если меньше единицы, то детали будут наоборот ослабляться (const=0.5), но это не будет эквивалентно простому сглаживанию, «контраст картинки» останется:
Обратите внимание, что мой код генерирует файл 3Д модели в формате Wavefront .obj, рендерил я в сторонней программе. Посмотреть получившуюся модель можно, например, в онлайн-вьюере. Если вам интересны именно методы отрисовки, а не генерирование модели, то читайте мой курс лекций по компьютерной графике.
Пример 3: добавляем ограничения
Давайте вернёмся к самому первому примеру, и сделаем ровно то же самое, но только не будем переписывать элементы массива под номерами 0, 18 и 31:
Остальные, «свободные» элементы массива я инициализировал нулями, и по-прежнему итеративно заменяю их на среднее значение соседних элементов. Вот так выглядит эволюция массива на первых ста пятидесяти итерациях:
Вполне очевидно, что на сей раз решение сойдётся не к постоянному элементу, заполняющему массив, а к двум линейным рампам. Кстати, действительно ли всем очевидно? Если нет, то экспериментируйте с этим кодом, я специально привожу примеры с очень коротким кодом, чтобы можно было досконально разобраться с происходящим.
Лирическое отступление: численное решение систем линейных уравнений.
Пусть нам дана обычная система линейных уравнений:
Её можно переписать, оставив в каждом из уравнений с одной стороны знака равенства x_i:
Пусть нам дан произвольный вектор 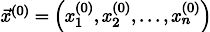
Тогда, воткнув его в правую часть нашей системы, мы можем получить обновлённый вектор приближения решения 
Чтобы было понятнее, x1 получается из x0 следующим образом:
Повторив процесс k раз, решение будет приближено вектором
Давайте на всякий случай запишем рекурретную формулу:
При некоторых предположениях о коэффициентах системы (например, вполне очевидно, что диагональные элементы не должны быть нулевыми, т.к. мы на них делим), данная процедура сходится к истинному решению. Эта гимнастика известна в литературе под названием метода Якоби. Конечно же, существуют и другие методы численного решения систем линейных уравнений, причём значительно более мощные, например, метод сопряжённых градиентов, но, пожалуй, метод Якоби является одним из самых простых.
Пример 3 ещё раз, но уже с другой стороны
А теперь давайте ещё раз внимательно посмотрим на основной цикл из примера 3:
Я стартовал с какого-то начального вектора x, и тысячу раз его обновляю, причём процедура обновления подозрительно похожа на метод Якоби! Давайте выпишем эту систему уравнений в явном виде:
Потратьте немного времени, убедитесь, что каждая итерация в моём питоновском коде — это строго одно обновление метода Якоби для этой системы уравнений. Значения x[0], x[18] и x[31] у меня зафиксированы, соответственно, в набор переменных они не входят, поэтому они перенесены в правую часть.
Итого, все уравнения в нашей системе выглядят как — x[i-1] + 2 x[i] — x[i+1] = 0. Это выражение не что иное, как обычные конечные разности для второй производной. То есть, наша система уравнений нам просто-напросто предписывает, что вторая производная должна быть везде равна нулю (ну, кроме как в точке x[18]). Помните, я говорил, что вполне очевидно, что итерации должны сойтись к линейным рампам? Так именно поэтому, у линейной функции вторая производная нулевая.
А вы знаете, что мы с вами только что решили задачу Дирихле для уравнения Лапласа?
Кстати, внимательный читатель должен был бы заметить, что, строго говоря, у меня в коде системы линейных уравнений решаются не методом Якоби, но методом Гаусса-Зейделя, который является своебразной оптимизацией метода Якоби:
Пример 4: уравнение Пуассона
А давайте мы самую малость изменим третий пример: каждая ячейка помещается не просто в центр масс соседних ячеек, но в центр масс плюс некая (произвольная) константа:
В прошлом примере мы выяснили, что помещение в центр масс — это дискретизация оператора Лапласа (в нашем случае второй производной). То есть, теперь мы решаем систему уравнений, которая говорит, что наш сигнал должен иметь некую постоянную вторую производную. Вторая производная — это кривизна поверхности; таким образом, решением нашей системы должна стать кусочно-квадратичная функция. Проверим на дискретизации в 32 сэмпла:
При длине массива в 32 элемента наша система сходится к решению за пару сотен итераций. А что будет, если мы попробуем массив в 128 элементов? Тут всё гораздо печальнее, количество итераций нужно уже исчислять тысячами:
Метод Гаусса-Зейделя крайне прост в программировании, но малоприменим для больших систем уравнений. Можно попытаться его ускорить, применяя, например, многосеточные методы. На словах это может звучать громоздко, но идея крайне примитивная: если мы хотим решение с разрешением в тысячу элементов, то можно для начала решить с десятью элементами, получив грубую аппроксимацию, затем удвоить разрешение, решить ещё раз, и так далее, пока не достигнем нужного результата. На практике это выглядит следующим образом:
А можно не выпендриваться, и использовать настоящие солверы систем уравнений. Вот я решаю этот же пример, построив матрицу A и столбец b, затем решив матричное уравнение Ax=b:
А вот так выглядит результат работы этой программы, заметим, что решение получилось мгновенно:
Таким образом, действительно, наша функция кусочно-квадратичная (вторая производная равна константе). В первом примере мы задали нулевую вторую производную, в третьем ненулевую, но везде одинаковую. А что было во втором примере? Мы решили дискретное уравнение Пуассона, задав кривизну поверхности. Напоминаю, что произошло: мы посчитали кривизну входящей поверхности. Если мы решим задачу Пуассона, задав кривизну поверхности на выходе равной кривизне поверхности на входе (const=1), то ничего не изменится. Усиление характеристических черт лица происходит, когда мы просто увеличиваем кривизну (const=2.1). А если const Скрытый текст
Это результат по умолчанию, рыжий Ленин — это начальные данные, голубая кривая — это их эволюция, в бесконечности результат сойдётся в точку:
А вот результат с коэффицентом 2.:
Домашнее задание: почему во втором случае Ленин сначала превращается в Дзержинского, а затем снова сходится к Ленину же, но большего размера?
Заключение
Очень много задач обработки данных, в частности, геометрии, могут формулироваться как решение системы линейных уравнений. В данной статье я не рассказал, как строить эти системы, моей целью было лишь показать, что это возможно. Темой следующей статьи будет уже не «почему», но «как», и какие солверы потом использовать.
Кстати, а ведь в названии статьи присутствуют наименьшие квадраты. Увидели ли вы их в тексте? Если нет, то это абсолютно не страшно, это именно ответ на вопрос «как?». Oставайтесь на линии, в следующей статье я покажу, где именно они прячутся, и как их модифицировать, чтобы получить доступ к крайне мощному инструменту обработки данных. Например, в десяток строк кода можно получить вот такое:
Метод наименьших квадратов (МНК), линейная аппроксимация
Постановка задачи на конкретном примере
Предположим, имеются два показателя X и Y. Причем Y зависит от X. Так как МНК интересует нас с точки зрения регрессионного анализа (в Excel его методы реализуются с помощью встроенных функций), то стоит сразу же перейти к рассмотрению конкретной задачи.
Итак, пусть X — торговая площадь продовольственного магазина, измеряемая в квадратных метрах, а Y — годовой товарооборот, определяемый в миллионах рублей.
Требуется сделать прогноз, какой товарооборот (Y) будет у магазина, если у него та или иная торговая площадь. Очевидно, что функция Y = f (X) возрастающая, так как гипермаркет продает больше товаров, чем ларек.
Наборы данных
Метод наименьших квадратов используется для обработки набора данных и прогнозирования будущих значений. Пусть у нас есть массивы данных X = <10, 12, 14, 16, 18, 20>и Y = <18, 22, 24, 26, 27, 28>, при этом значение Y зависит от X. Придадим этим массивам смысл. К примеру, массив X – это мощность паровой машины парохода, а Y — его ходовая скорость в узлах. Это означает, что при мощности энергетической установки в 10 тысяч лошадиных сил, пароход развивает скорость на уровне 18 морских миль в час, и так далее, так как каждое значение игрека соответствует своему иксу.
Эти данные можно представить в виде точек на декартовой плоскости, например как V1(X1, Y1), V2(X2, Y2) и так далее. Если соединить эти точки, то мы получим некую кривую, которую можем описать соответствующим уравнением y = f(x). Данное уравнение должно быть достаточно простым, но при этом максимально близко описывать полученную зависимость.
Получив кривую, мы можем продлить ее в любую сторону и узнать приблизительное значение игреков для любых иксов или наоборот. Например, аппроксимировав данные нашего примера, мы сможем узнать, какая мощность установки требуется для достижения скорости в 15 узлов. Или какую мы получим скорость, установив на борт установку мощностью в 22 тысячи лошадиных сил. Для того чтобы определить эту волшебную y = f(x), нам и необходим метод наименьших квадратов.
Графическая иллюстрация метода наименьших квадратов (мнк).
На графиках все прекрасно видно. Красная линия – это найденная прямая y = 0.165x+2.184, синяя линия – это 
Для чего это нужно, к чему все эти аппроксимации?
Я лично использую для решения задач сглаживания данных, задач интерполяции и экстраполяции (в исходном примере могли бы попросить найти занчение наблюдаемой величины y при x=3 или при x=6 по методу МНК). Но подробнее поговорим об этом позже в другом разделе сайта.
Чтобы при найденных а и b функция принимала наименьшее значение, необходимо чтобы в этой точке матрица квадратичной формы дифференциала второго порядка для функции 
Дифференциал второго порядка имеет вид:
То есть
Следовательно, матрица квадратичной формы имеет вид
причем значения элементов не зависят от а и b .
Покажем, что матрица положительно определенная. Для этого нужно, чтобы угловые миноры были положительными.
Угловой минор первого порядка 

Угловой минор второго порядка
Докажем, что 
Проверим справедливость неравенства для любого значения n, например для n=2.
Получили верное неравенство для любых несовпадающих значений 

Предполагаем, что неравенство верное для n.

Докажем, что неравенство верное для n+1.
То есть, нужно доказать, что 

Поехали.
Выражение в фигурных скобках положительно по предположению пункта 2), а остальные слагаемые положительны, так как представляют собой квадраты чисел. Этим доказательство завершено.
Вывод : найденные значения а и b соответствуют наименьшему значению функции 
Сглаживание ряда методом наименьших квадратов
Задание.
1. Постройте прогноз численности наличного населения города Б на 2010-2011 гг., используя методы: скользящей средней , экспоненциального сглаживания , наименьших квадратов .
2. Постройте график фактического и расчетных показателей.
3. Рассчитайте ошибки полученных прогнозов при использовании каждого метода.
4. Сравните полученные результаты, сделайте вывод.
Решение.
1. Находим параметры уравнения методом наименьших квадратов. Линейное уравнение тренда имеет вид y = bt + a
Система уравнений МНК:
a0n + a1∑t = ∑y
a0∑t + a1∑t 2 = ∑y•t
| t | y | t 2 | y 2 | t•y |
| 1 | 58.8 | 1 | 3457.44 | 58.8 |
| 2 | 58.7 | 4 | 3445.69 | 117.4 |
| 3 | 59 | 9 | 3481 | 177 |
| 4 | 59 | 16 | 3481 | 236 |
| 5 | 58.8 | 25 | 3457.44 | 294 |
| 6 | 58.3 | 36 | 3398.89 | 349.8 |
| 7 | 57.9 | 49 | 3352.41 | 405.3 |
| 8 | 57.5 | 64 | 3306.25 | 460 |
| 9 | 56.9 | 81 | 3237.61 | 512.1 |
| 45 | 524.9 | 285 | 30617.73 | 2610.4 |
Для наших данных система уравнений имеет вид:
9a0 + 45a1 = 524.9
45a0 + 285a1 = 2610.4
Из первого уравнения выражаем а0 и подставим во второе уравнение
Получаем a0 = -0.24, a1 = 59.5
Уравнение тренда:
y = -0.24 t + 59.5
Эмпирические коэффициенты тренда a и b являются лишь оценками теоретических коэффициентов βi, а само уравнение отражает лишь общую тенденцию в поведении рассматриваемых переменных.
Коэффициент тренда b = -0.24 показывает среднее изменение результативного показателя (в единицах измерения у) с изменением периода времени t на единицу его измерения. В данном примере с увеличением t на 1 единицу, y изменится в среднем на -0.24.
Ошибка аппроксимации.
Оценим качество уравнения тренда с помощью ошибки абсолютной аппроксимации.
Ошибка аппроксимации в пределах 5%-7% свидетельствует о хорошем подборе уравнения тренда к исходным данным.
Поскольку ошибка меньше 7%, то данное уравнение можно использовать в качестве тренда.
Однофакторный дисперсионный анализ.
Средние значения
Дисперсия
Среднеквадратическое отклонение
Коэффициент эластичности.
Коэффициент эластичности представляет собой показатель силы связи фактора t с результатом у, показывающий, на сколько процентов изменится значение у при изменении значения фактора на 1%.
Коэффициент эластичности меньше 1. Следовательно, при изменении t на 1%, Y изменится менее чем на 1%. Другими словами – влияние t на Y не существенно.
Эмпирическое корреляционное отношение.
Эмпирическое корреляционное отношение вычисляется для всех форм связи и служит для измерение тесноты зависимости. Изменяется в пределах [0;1].
где ( y -yt)² = 4.4-1.08 = 3.31
В отличие от линейного коэффициента корреляции он характеризует тесноту нелинейной связи и не характеризует ее направление. Изменяется в пределах [0;1].
Связи между признаками могут быть слабыми и сильными (тесными). Их критерии оцениваются по шкале Чеддока:
0.1 0.3 0.5 0.7 0.9 Полученная величина свидетельствует о том, что изменение временного периода t существенно влияет на y.
Коэффициент детерминации.
т.е. в 75.39% случаев влияет на изменение данных. Другими словами – точность подбора уравнения тренда – высокая.
| t | y | y(t) | (y-ycp) 2 | (y-y(t)) 2 | (t-tp) 2 | (y-y(t)) : y |
| 1 | 58.8 | 59.26 | 0.23 | 0.21 | 16 | 0.00786 |
| 2 | 58.7 | 59.03 | 0.14 | 0.11 | 9 | 0.00557 |
| 3 | 59 | 58.79 | 0.46 | 0.0431 | 4 | 0.00352 |
| 4 | 59 | 58.56 | 0.46 | 0.2 | 1 | 0.0075 |
| 5 | 58.8 | 58.32 | 0.23 | 0.23 | 0 | 0.00813 |
| 6 | 58.3 | 58.09 | 0.0004 | 0.0452 | 1 | 0.00365 |
| 7 | 57.9 | 57.85 | 0.18 | 0.0022 | 4 | 0.000825 |
| 8 | 57.5 | 57.62 | 0.68 | 0.0137 | 9 | 0.00204 |
| 9 | 56.9 | 57.38 | 2.02 | 0.23 | 16 | 0.00847 |
| 45 | 524.9 | 524.9 | 4.4 | 1.08 | 60 | 0.0476 |
Интервальный прогноз.
Определим среднеквадратическую ошибку прогнозируемого показателя.
m = 1 – количество влияющих факторов в уравнении тренда.
Uy=yn+L±K
где
L – период упреждения; уn+L – точечный прогноз по модели на (n + L)-й момент времени; n – количество наблюдений во временном ряду; Sy – стандартная ошибка прогнозируемого показателя; Tтабл – табличное значение критерия Стьюдента для уровня значимости α и для числа степеней свободы, равного n-2.
По таблице Стьюдента находим Tтабл
Tтабл (n-m-1;α/2) = (7;0.025) = 2.365
Точечный прогноз, t = 10: y(10) = -0.24*10 + 59.5 = 57.15
57.15 – 1.08 = 56.07 ; 57.15 + 1.08 = 58.23
Интервальный прогноз:
t = 10: (56.07;58.23)
Точечный прогноз, t = 11: y(11) = -0.24*11 + 59.5 = 56.91
56.91 – 1.14 = 55.77 ; 56.91 + 1.14 = 58.05
Интервальный прогноз:
t = 11: (55.77;58.05)
2. Сглаживаем ряд методом скользящей средней. Одним из эмпирических методов является метод скользящей средней. Этот метод состоит в замене абсолютных уровней ряда динамики их средними арифметическими значениями за определенные интервалы. Выбираются эти интервалы способом скольжения: постепенно исключаются из интервала первые уровни и включаются последующие.
| t | y | ys | Формула |
| 1 | 58.8 | 58.75 | (58.8 + 58.7)/2 |
| 2 | 58.7 | 58.85 | (58.7 + 59)/2 |
| 3 | 59 | 59 | (59 + 59)/2 |
| 4 | 59 | 58.9 | (59 + 58.8)/2 |
| 5 | 58.8 | 58.55 | (58.8 + 58.3)/2 |
| 6 | 58.3 | 58.1 | (58.3 + 57.9)/2 |
| 7 | 57.9 | 57.7 | (57.9 + 57.5)/2 |
| 8 | 57.5 | 57.2 | (57.5 + 56.9)/2 |
| 9 | 56.9 | – | – |
Стандартная ошибка (погрешность) рассчитывается по формуле:
где i = (t-m-1, t)
3. Построим прогноз численности с использованием экспоненциального сглаживания. Важным методом стохастических прогнозов является метод экспоненциального сглаживания. Этот метод заключается в том, что ряд динамики сглаживается с помощью скользящей средней, в которой веса подчиняются экспоненциальному закону.
Эту среднюю называют экспоненциальной средней и обозначают St.
Она является характеристикой последних значений ряда динамики, которым присваивается наибольший вес.
Экспоненциальная средняя вычисляется по рекуррентной формуле:
St = α*Yt + (1- α)St-1
где St – значение экспоненциальной средней в момент t;
St-1 – значение экспоненциальной средней в момент (t = 1);
Что касается начального параметра S0, то в задачах его берут или равным значению первого уровня ряда у1, или равным средней арифметической нескольких первых членов ряда.
Yt – значение экспоненциального процесса в момент t;
α – вес t-ого значения ряда динамики (или параметр сглаживания).
Последовательное применение формулы дает возможность вычислить экспоненциальную среднюю через значения всех уровней данного ряда динамики.
Наиболее важной характеристикой в этой модели является α, по величине которой практически и осуществляется прогноз. Чем значение этого параметра ближе к 1, тем больше при прогнозе учитывается влияние последних уровней ряда динамики.
Если α близко к 0, то веса, по которым взвешиваются уровни ряда динамики убывают медленно, т.е. при прогнозе учитываются все прошлые уровни ряда.
В специальной литературе отмечается, что обычно на практике значение α находится в пределах от 0,1 до 0,3. Значение 0,5 почти никогда не превышается.
Экспоненциальное сглаживание применимо, прежде всего, при постоянном объеме потребления (α = 0,1 – 0,3). При более высоких значениях (0,3 – 0,5) метод подходит при изменении структуры потребления, например, с учетом сезонных колебаний.
В качестве S0 берем первое значение ряда, S0 = y1 = 58.8
| t | y | St | Формула |
| 1 | 58.8 | 58.8 | (1 – 0.1)*58.8 + 0.1*58.8 |
| 2 | 58.7 | 58.71 | (1 – 0.1)*58.7 + 0.1*58.8 |
| 3 | 59 | 58.97 | (1 – 0.1)*59 + 0.1*58.71 |
| 4 | 59 | 59 | (1 – 0.1)*59 + 0.1*58.97 |
| 5 | 58.8 | 58.82 | (1 – 0.1)*58.8 + 0.1*59 |
| 6 | 58.3 | 58.35 | (1 – 0.1)*58.3 + 0.1*58.82 |
| 7 | 57.9 | 57.95 | (1 – 0.1)*57.9 + 0.1*58.35 |
| 8 | 57.5 | 57.54 | (1 – 0.1)*57.5 + 0.1*57.95 |
| 9 | 56.9 | 56.96 | (1 – 0.1)*56.9 + 0.1*57.54 |
Прогнозирование данных с использованием экспоненциального сглаживания.
Методы прогнозирования под названием “сглаживание” учитывают эффекты выброса функции намного лучше, чем способы, использующие регрессивный анализ.
Базовое уравнение имеет следующий вид:
F(t+1) = F(t)(1 – α) + αY(t)
F(t) – это прогноз, сделанный в момент времени t; F(t+1) отражает прогноз во временной период, следующий непосредственно за моментом времени t
Стандартная ошибка (погрешность) рассчитывается по формуле:
где i = (t – 2, t)
Пример . Методом наименьших квадратов найти функции вида y=ax+b , y=ax²+bx+c , аппроксимирующие экспериментальную функцию y=f(x) . В обоих случаях найти суммы квадратов невязок ∑bi². В декартовой системе координат построить экспериментальные точки и графики найденных функций y=ax+b,y=ax^2+bx+c.
Пример №5
Пример №3 . Функция y=y(x) задана таблицей своих значений:
x: -2 -1 0 1 2
y: -0,8 -1,6 -1,3 0,4 3,2
Применяя метод наименьших квадратов, приблизить функцию многочленами 1-ой и 2-ой степеней. Для каждого приближения определить величину среднеквадратичной погрешности. Построить точечный график функции и графики многочленов.
Решение. Функция многочлена 2-ой степени имеет вид y = ax 2 + bx + c .
1. Находим параметры уравнения методом наименьших квадратов. Система уравнений МНК:
a0n + a1∑x + a2∑x 2 = ∑y
a0∑x + a1∑x 2 + a2∑x 3 = ∑yx
a0∑x 2 + a1∑x 3 + a2∑x 4 = ∑yx 2
http://habr.com/ru/post/429980/
http://exceltut.ru/metod-naimenshih-kvadratov-mnk-linejnaya-approksimatsiya/