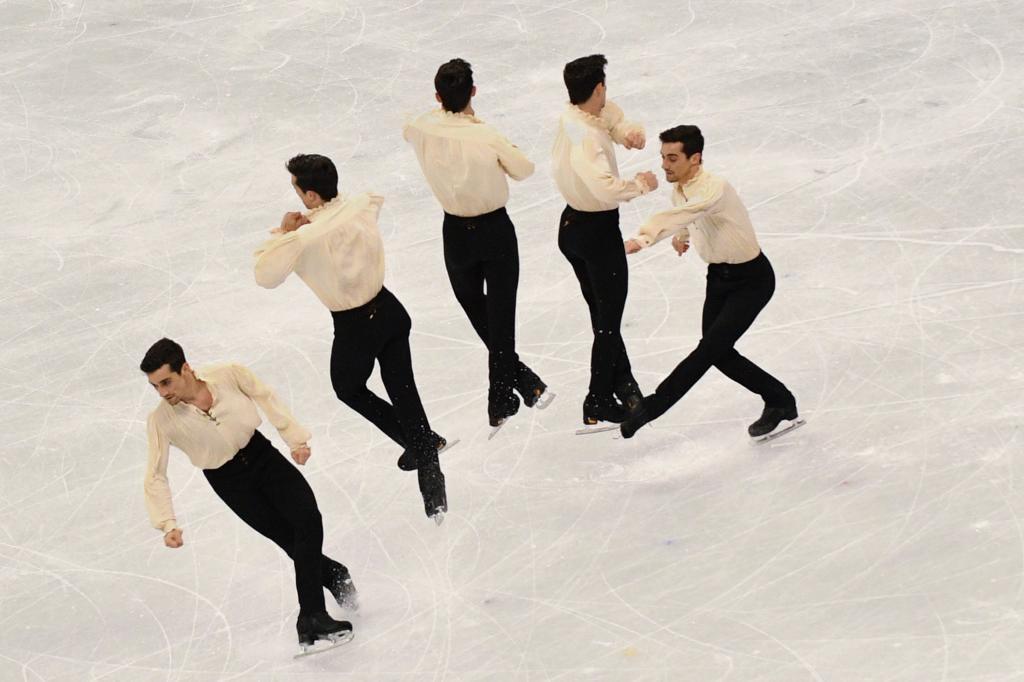Вывести уравнение моментов dl dt m

Вращательное движение тела. Закон вращательного движения

В этой статье описывается важный раздел физики — «Кинематика и динамика вращательного движения».

Основные понятия кинематики вращательного движения

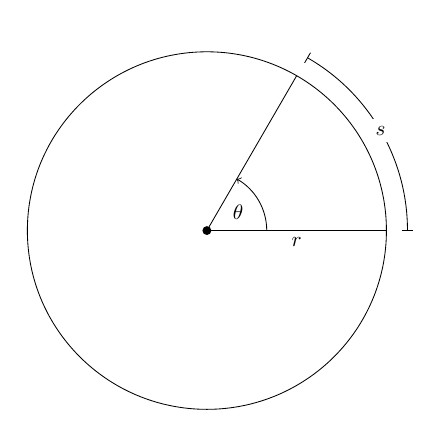
Вращательным движением материальной точки вокруг неподвижной оси называют такое движение, траекторией которого является окружность, находящаяся в плоскости перпендикулярной к оси, а центр ее лежит на оси вращения.

Вращательное движение твердого тела — это движение, при котором по концентрическим (центры которых лежат на одной оси) окружностям движутся все точки тела в соответствии с правилом для вращательного движения материальной точки.

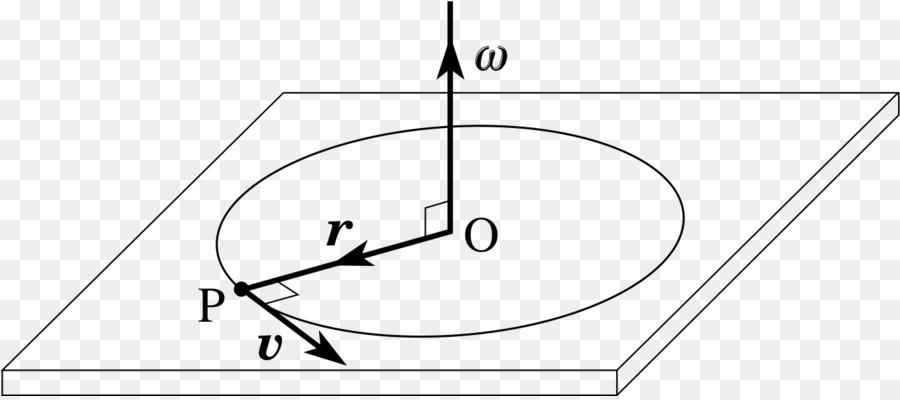
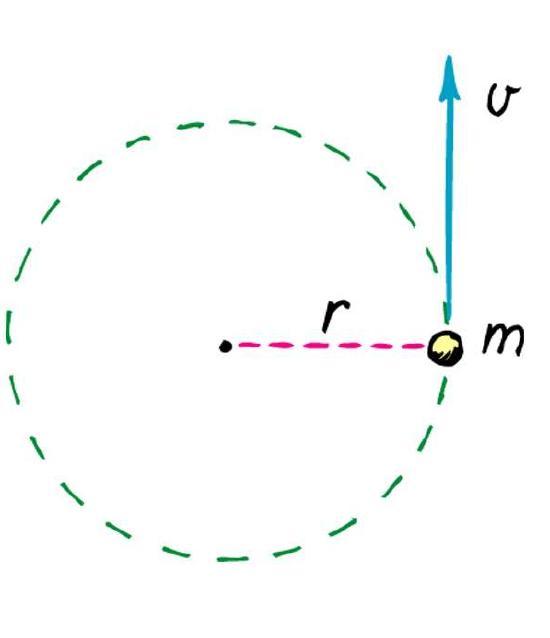
Пусть произвольное твердое тело T совершает вращения вокруг оси O, которая перпендикулярна плоскости рисунка. Выберем на данном теле точку M. При вращении эта точка будет описывать вокруг оси O круг радиусом r.

Через некоторое время радиус повернется относительно исходного положения на угол Δφ.

За положительное направление поворота принято направление правого винта (по часовой стрелке). Изменение угла поворота со временем называется уравнением вращательного движения твердого тела:

Если φ измерять в радианах (1 рад — это угол, соответствующий дуге, длиной равной ее радиусу), то длина дуги окружности ΔS, которую пройдет материальная точка M за время Δt, равна:

Основные элементы кинематики равномерного вращательного движения

Мерой перемещения материальной точки за небольшой промежуток времени dt служит вектор элементарного поворота dφ.

Угловая скорость материальной точки или тела — это физическая величина, которая определяется отношением вектора элементарного поворота к продолжительности этого поворота. Направление вектора можно определить правилом правого винта вдоль оси О. В скалярном виде:

Если ω = dφ/dt = const, то такое движение называется равномерное вращательное движение. При нем угловую скорость определяют по формуле

Согласно предварительной формуле размерность угловой скорости

Равномерное вращательное движение тела можно описать периодом вращения. Период вращения T — физическая величина, определяющая время, за которое тело вокруг оси вращения выполняет один полный оборот ([T] = 1 с). Если в формуле для угловой скорости принять t = T, φ = 2 π (полный один оборот радиуса r), то

поэтому период вращения определим следующим образом:

Число оборотов, которое за единицу времени совершает тело, называется частотой вращения ν, которая равна:

Единицы измерения частоты: [ν]= 1/c = 1 c -1 = 1 Гц.

Сравнивая формулы для угловой скорости и частоты вращения, получим выражение, связывающее эти величины:

Основные элементы кинематики неравномерного вращательного движения

Неравномерное вращательное движение твердого тела или материальной точки вокруг неподвижной оси характеризует его угловая скорость, которая изменяется со временем.

Вектор ε, характеризующий скорость изменения угловой скорости, называется вектором углового ускорения:

Если тело вращается, ускоряясь, то есть dω/dt > 0, вектор имеет направление вдоль оси в ту же сторону, что и ω.

Если вращательное движение замедлено — dω/dt 2 /r = ω 2 r 2 /r.

Итак, в скалярном виде

Тангенциальное ускоренной материальной точки, которая выполняет вращательное движение

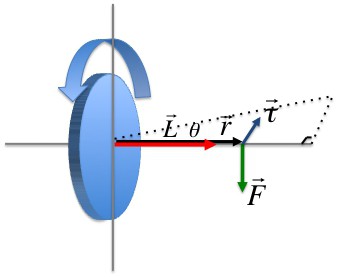
Момент импульса материальной точки

Векторное произведение радиуса-вектора траектории материальной точки массой m_i на ее импульс называется моментом импульса этой точки касательно оси вращения. Направление вектора можно определить, воспользовавшись правилом правого винта.

Момент импульса материальной точки (L_i) направлен перпендикулярно плоскости, проведенной через r_i и υ_i, и образует с ними правую тройку векторов (то есть при движении с конца вектора r_i к υ_i правый винт покажет направление вектора L_i).

В скалярной форме

Учитывая, что при движении по кругу радиус-вектор и вектор линейной скорости для i-й материальной точки взаимно перпендикулярные,

Так что момент импульса материальной точки для вращательного движения примет вид

Момент силы, которая действует на i-ю материальную точку

Векторное произведение радиуса-вектора, который проведен в точку приложения силы, на эту силу называется моментом силы, действующей на i-ю материальную точку относительно оси вращения.

В скалярной форме

Величина l_i, равная длине перпендикуляра, опущенного из точки вращения на направление действия силы, называется плечом силы F_i.

Динамика вращательного движения

Уравнение динамики вращательного движения записывается так:

Формулировка закона следующая: скорость изменения момента импульса тела, которое совершает вращение вокруг неподвижной оси, равна результирующему моменту относительно этой оси всех внешних сил, приложенных к телу.

Момент импульса и момент инерции

Известно, что для i-й материальной точки момент импульса в скалярной форме задается формулой

Если вместо линейной скорости подставить ее выражение через угловую:

то выражение для момента импульса примет вид

Величина I_i = m_ir_i 2 называется моментом инерции относительно оси i-й материальной точки абсолютно твердого тела, проходящей через его центр масс. Тогда момент импульса материальной точки запишем:

Момент импульса абсолютно твердого тела запишем как сумму моментов импульса материальных точек, составляющих данное тело:

Момент силы и момент инерции

Закон вращательного движения гласит:

Известно, что представить момент импульса тела можно через момент инерции:

Учитывая, что угловое ускорение определяется выражением

получим формулу для момента силы, представленного через момент инерции:

Замечание. Момент силы считается положительным, если угловое ускорение, которым он вызван, больше нуля, и наоборот.

Теорема Штейнера. Закон сложения моментов инерции

Если ось вращения тела через центр масс его не проходит, то относительно этой оси можно найти его момент инерции по теореме Штейнера:
I = I₀ + ma 2 ,

где I₀ — начальный момент инерции тела; m — масса тела; a — расстояние между осями.

Если система, которая совершает обороты округ неподвижной оси, состоит из n тел, то суммарный момент инерции такого типа системы будет равен сумме моментов, ее составляющих (закон сложения моментов инерции).

Классическая физика определяет момент импульса твёрдого тела как скорость изменения некоего произвольного вектора (А), связанного с центром масс тела, т.е. с неинерциальной системой координат относительно инерциальной системы координат. Вычисляя производные для каждой из осей инерциальной системы координат, и применяя их к основному уравнению динамики вращательного движения в уравнении второго закона Ньютона простой механической заменой переменных получают уравнения Эйлера. Для этого производную вектора (А) в инерциальной системе координат ( dA / dt ) заменяют новой переменной – моментом силы (М), а производную этого же вектора в подвижной системе координат (∂ A /∂ t ), связанной с телом, но в предположении, что, что оси ( i ‘, j ‘, k ‘) неподвижны, заменяют новой переменной – моментом импульса ( dL / dt )!

Приведём курсивом классический вывод уравнений Эйлера (см. упомянутую выше работу Матвеева А. Н. на стр. 317 – 319.):

Уравнение движения центра масс тела имеет вид:

r ₀ : радиус–вектор центра масс тела, проведённый из точки его закрепления. Реакции связи включены в ( F ).

Пусть некоторый вектор (А) задан компонентами относительно системы координат ( i ‘, j ‘, k ‘):

С течением времени изменяются компоненты ( A ‘ _x , A ‘ _y , A ‘ _z ) относительно движущихся осей координат и ориентировка осей координат относительно инерциальной системы отсчёта.

Скорость точки вращающегося тела, радиус–вектор которой ( r ), равна ( dr / dt = [ ω , r ]). Аналогично, следя за концом вектора ( i ‘), проведённым из точки на оси вращения, находим ( d i ‘ / dt = [ ω , i ‘]). Такой же вид имеют производные от ( j ) и ( k ). Следовательно, ориентировку осей координат с проекциями вектора (А) подвижной системы отсчёта относительно инерциальной системы отсчёта ( d i ‘ / dt * A ‘ _x + d j ‘ / dt * A ‘ _y + dk ‘ / dt * A ‘ _z ) можно выразить следующим образом:

dA / dt = ∂A / ∂t + [ω, A],

где (∂ A / ∂ t ) есть производная от (А), вычисленная в предположении, что оси ( i ‘, j ‘, k ‘) неподвижны:

∂A / ∂t = i’ * dA’_x / dt + j’ * dA’y / dt + k’ * dA’_z / dt

Утверждается, что эта формула справедлива для любых векторов (А). На этом основании после замены переменных, получают следующее выражение:

Принимая во внимание, что ( L_x = I_x * ω _x ), ( L_y = I_y * ω _y ), ( L_z = I_z * ω _z ) последнее выражение, полученное после замены переменных, переписывают в компонентах относительно движущейся системы координат для каждой из осей координат (штрихи опущены):

Это и есть уравнения Эйлера. Классическая физика утверждает, что эти уравнения всегда позволяют определить вращательное движение тела, закреплённого в одной точке. Однако уравнения Эйлера не отражают физическую реальность, т.к. это есть некорректная попытка смешать в одной общей зависимости одноимённые параметры разных видов вращательного движения по радиусу, которые физически могут существовать только автономно в своих собственных системах отсчёта, определяемых именно своим постоянным во всех отношениях радиусом. В общем результирующем движении нет, и не может быть автономных вращений разных масс, хотя и одного тела, но расположенных на разных радиусах по абсолютной величине и осуществляющихся в разных плоскостях. Они существуют только в соответствии с абстрактными математическими представлениями классической динамики вращательного движения.

Вывод уравнений Эйлера представляет собой обычное дифференцирование уравнения второго закона Ньютона, в котором ускорение представлено как дифференциал скорости ( dA / dt ). При этом замена переменных произведена на том основании, что второй закон Ньютона якобы является полным физическим аналогом уравнения моментов. Однако, как показано в главе (3) физической аналогии между классической динамикой вращательного движения и динамикой Ньютона нет. Напомним коротко суть этого несоответствия.

Угловое перемещение определяется из внешней точки отсчёта как угловой размер видимой из этой точки длины линейного перемещения. Однако динамика Ньютона, определяющая динамику вращательного движения, не ограничена ни величиной, ни направлением перемещения в пространстве. Поэтому для объективной и однозначной оценки ограниченного 360–ю градусами углового перемещения должны неукоснительно соблюдаться три условия:

1. Линейное движение тела должно осуществляться на постоянном фиксированном расстоянии от точки отсчёта, т.к. радиальное движение искажает угловой размер даже неизменной линейной траектории.

2. Угловое перемещение определяется из внешней точки наблюдения между двумя направлениями на точки изменяющегося положения центра масс движущегося тела. Это означает, что вместе с точкой отсчёта угловое перемещение определяется тремя точками, через которые одновременно можно провести только одну плоскость. Следовательно, для однозначного определения углового перемещения вращательное движение точки должно осуществляться только в одной плоскости.

3. Первое условие может соблюдаться только при движении тела по окружности, в котором обеспечивается равновесие центробежной и центростремительной силы. В неравномерном движении по окружности с постоянным радиусом это равновесие так же соблюдается только каждый раз на новом энергетическом уровне (см. гл. 7.3).

Перечисленные выше условия могут соблюдаться только относительно вполне определённой точки отсчёта, с которой движущееся тело связано физически либо жесткой механической, либо полевой связью. Третье условие является следствием из первых двух. Однако физически первые два условия обеспечиваются именно третьим условием, т.к. нельзя достоверно определить динамику движения, если исключается его физическая основа – точка его отсчёта.

Именно эти три условия и определяют, как само вращательное движение, так и его динамику. Никакой динамики вращательного движения с переменным радиусом относительно произвольной точки отсчёта и с переменной плоскостью его вращения не может быть в принципе. Радиус это только безразмерный коэффициент связи углового перемещения с линейным. Поэтому динамика вращательного движения может корректно описывать только динамику переменного окружного движения, физически привязанного к постоянному по абсолютной величине радиусу и к постоянной плоскости вращения.

В выводе уравнений Эйлера тело жестко связано с подвижной системой отсчёта, в которой плоскость предполагаемого вращения не изменяется. Следовательно, вектор (А) относительно осей подвижной системы координат можно условно сопоставить с моментом импульса, но только, если его изменения по абсолютной величине обусловлены изменением только параметров динамики окружного движения и не связаны с изменением длины радиуса. Однако в выводе Эйлера эти условия не соблюдаются.

Кроме того, у Эйлера есть ещё и проекции вектора (А) на оси неподвижной инерциальной системы координат, которые в любом случае нарушают три обязательных условия для динамики вращательного движения, что приводит к искажению реальной действительности. Причём в этом нет никакого противоречия с подобным использованием проекций Ньютоновских векторов исходного второго закона Ньютона.

Проецирование линейного движения на оси системы координат в Ньютоновской динамике это фактически оценка линейного движения со стороны, т.к. с реальным перемещением связано только его движение по фактической траектории. Однако в Ньютоновской динамике эти проекции применяются для достоверного определения исходного реального движения. А вот проекции векторов вращательного движения на любые оси, физически не связанные с вращательным движением это очередной абсурд классической физики.

Как отмечалось выше, вектора моментов вращательного движения и его угловой скорости уже сами по себе являются, оценкой вращательного движения из внешней точки, т.е. со стороны. Следовательно, в этом смысле они сами подобны виртуальным проекциям реального движения. Но голая геометрия проекции проекций не отражает реальную действительность. Поэтому в динамике Ньютона проекции проекций запрещены (см. гл. 3.5). Однако это не мешает классической физике применять такое некорректное проецирование в динамике вращательного движения.

Кроме того, вектора вращательного движения в отличие от Ньютоновских векторов не отражают никакого реального силового воздействия или движения в своём направлении. Их единственной физической основой является их физическая связь с осью именно своего вращения в соответствии с третьим условием, которое одновременно является физической основой первых двух условий. Поэтому оценка вращательного движения со стороны любых других не связанных со своим вращением осей, на которые их проецирует Эйлер и классическая физика грубо нарушает три перечисленных выше условия вращательного движения.

Любое линейное движение осуществляется под действием одной единственной результирующей силы. Это особенно актуально для криволинейного движения, в котором результирующая сила обобщает не просто ортогональные составляющие, а множество сил в произвольных направлениях. Когда результирующая сила от множества источников уже полностью сформирована, то физически на тело действует только одна сила. При этом все остальные силы как бы сливаются в едином источнике результирующей силы в одну силу. Но даже в этом случае реальную результирующую силу в динамике Ньютона можно оценить по её проекциям, условно допустив и измерив, ортогональные источники силы.

В динамике вращательного движения эта условность не соответствует реальной действительности. Например, классическая физика допускает располагать ось вращательного движения произвольно, не привязывая её к реальному вращательному движению физически, т.е. это только наблюдательная ось, с которой можно только наблюдать чужое движение.

При этом абстрактное угловое перемещение относительно произвольно выбранной оси можно определить и при движении тела по прямолинейной траектории и даже направить вдоль этой оси моменты. Однако прямая линия имеет бесконечный радиус. Поэтому такой момент фактически будет равен бесконечности, а угловая скорость движения по прямой линии фактически равна нулю, что не совпадает с абстрактными угловыми параметрами при движении вдоль прямой при их оценке со стороны.

На коротком отрезке траектории в минимальном интервале времени ( dt ) расстояние до прямолинейной траектории классическая физика принимает за конечный радиус и далее определяет все остальные параметры динамики такого псевдо вращения. Однако никакого вращательного движения при перемещении по прямой линии физически нет. Более того, в соответствии с классической динамикой вращательного движения ось и моменты могут располагаться даже с обратной стороны кривизны, что в частности проявляется при проецировании реальной кривой линии на оси прямоугольной системы координат.

При этом вместо того, чтобы подобно динамике Ньютона восстанавливать по этим проекциям реальные движение Эйлер осуществляет обратный процесс. Из полученных проекций он спокойно вычисляет параметры такого с позволения сказать либо прямолинейного, либо обратно–криволинейного вращения. Причём последнее теоретически должно иметь даже не нулевую кривизну и бесконечный радиус, как при движении по прямой линии, а отрицательную кривизну и отрицательный радиус! Однако прямолинейные и обратно–криволинейные виртуальные вращения Эйлера не имеют ничего общего с вращением ни по определению, ни физически!

Если в динамике Ньютона виртуальные проекции векторов реального физического перемещения в пространстве самого тела на ортогональные оси хотя бы отражают относительное линейное движение, то относительного вращения в природе не существует. Даже со стороны вращательное движение может быть косвенно оценено как вращение относительно своего же реального центра, т.е. вращение в своей собственной абсолютной системе координат. А вращения в одной плоскости относительно совпадающих в пространстве центров, но имеющие свою собственную физическую связь с центром – это индивидуальные вращения, но не одно общее вращение.

Поскольку всякая теория подкрепляется только опытом, покажем на конкретном примере, что из виртуальных проекций Эйлера в общем случае невозможно получить достоверные параметры динамики вращательного движения ни по направлению, ни по абсолютной величине. Рассмотрим для простоты динамику вращения твёрдого тела в виде плоского диска, изображённого на рисунке (4.7.1.1). На рисунке (4.7.1.1) показаны суммарные вращения диска по двум методам: по правилам классической динамики вращательного движения, т.е. складываются моменты якобы самостоятельных вращений вдоль главных осей; и второе в соответствии с базовой динамикой Ньютона, когда сначала находятся результирующие всех действующих сил, а затем вызванный ими результирующий момент.

Вращательное движение твердого тела: уравнение, формулы

В природе и технике мы часто сталкиваемся с проявлением вращательного движения твердых тел, например, валов и шестерен. Как в физике описывают этот тип движения, какие формулы и уравнения для этого применяются, эти и другие вопросы освещаются в данной статье.

Что такое вращение?

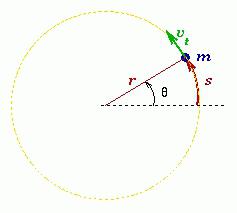
Каждый из нас интуитивно представляет, о каком движении пойдет речь. Вращение — это процесс, при котором тело или материальная точка движется по круговой траектории вокруг некоторой оси. С геометрической точки зрения ось вращения твердого тела — это прямая, расстояние до которой в процессе перемещения остается неизменным. Это расстояние называют радиусом вращения. Далее будем обозначать его буквой r. Если ось вращения проходит через центр масс тела, то ее называют собственной осью. Примером вращения вокруг собственной оси является соответствующее движение планет Солнечной системы.

Вам будет интересно: Афронт — это ситуация, в которой не хочется оказаться

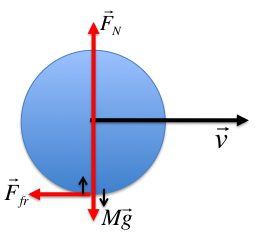
Чтобы вращение происходило, должно существовать центростремительное ускорение, которое возникает за счет центростремительной силы. Эта сила направлена от центра масс тела к оси вращения. Природа центростремительной силы может быть самой разной. Так, в космическом масштабе ее роль выполняет гравитация, если тело закреплено нитью, то сила натяжения последней будет центростремительной. Когда тело вращается вокруг собственной оси, роль центростремительной силы играет внутреннее электрохимическое взаимодействие между составляющими тело элементами (молекулами, атомами).

Вам будет интересно: Декабрист Оболенский Евгений Петрович: биография. Декабристские организации

Необходимо понимать, что без присутствия центростремительной силы тело будет двигаться прямолинейно.

Описывающие вращение физические величины

Во-первых, это динамические характеристики. К ним относятся:

• момент импульса L;
• момент инерции I;
• момент силы M.

Во-вторых, это кинематические характеристики. Перечислим их:

• угол поворота θ;
• скорость угловая ω;
• ускорение угловое α.

Кратко опишем каждую из названных величин.

Момент импульса определяется по формуле:

Где p — линейный импульс, m — масса материальной точки, v — ее линейная скорость.

Момент инерции материальной точки рассчитывается с помощью выражения:

Для любого тела сложной формы величина I рассчитывается, как интегральная сумма моментов инерции материальных точек.

Момент силы M вычисляется так:

Здесь F — внешняя сила, d — расстояние от точки ее приложения до оси вращения.

Физический смысл всех величин, в названии которых присутствует слово «момент», аналогично смыслу соответствующих линейных величин. Например, момент силы показывает возможность приложенной силы сообщить угловое ускорение системе вращающихся тел.

Кинематические характеристики математически определяются следующими формулами:

Как видно из этих выражений, угловые характеристики аналогичны по своему смыслу линейным (скорости v и ускорению a), только они применимы для круговой траектории.

Динамика вращения

В физике изучение вращательного движения твердого тела осуществляется с помощью двух разделов механики: динамики и кинематики. Начнем с динамики.

Динамика изучает внешние силы, действующие на систему вращающихся тел. Сразу запишем уравнение вращательного движения твердого тела, а затем, разберем его составные части. Итак, это уравнение имеет вид:

Момент силы, который действует на систему, обладающую моментом инерции I, вызывает появление углового ускорения α. Чем меньше величина I, тем легче с помощью определенного момента M раскрутить систему до больших скоростей за малые промежутки времени. Например, металлический стержень легче вращать вдоль его оси, чем перпендикулярно ей. Однако, тот же стержень легче вращать вокруг оси, перпендикулярной ему, и проходящей через центр масс, чем через его конец.

Закон сохранения величины L

Выше была введена эта величина, она называется моментом импульса. Уравнение вращательного движения твердого тела, представленное в предыдущем пункте, часто записывают в иной форме:

Если момент внешних сил M действует на систему в течение времени dt, то он вызывает изменение момента импульса системы на величину dL. Соответственно, если момент сил равен нулю, тогда L = const. Это и есть закон сохранения величины L. Для нее, используя связь между линейной и угловой скоростью, можно записать:

L = m*v*r = m*ω*r2 = I*ω.

Таким образом, при отсутствии момента сил произведение угловой скорости и момента инерции является постоянной величиной. Этот физический закон используют фигуристы в своих выступлениях или искусственные спутники, которые необходимо повернуть вокруг собственной оси в открытом космосе.

Центростремительное ускорение

Выше, при изучении вращательного движения твердого тела, уже была описана эта величина. Также была отмечена природа центростремительных сил. Здесь лишь дополним эту информацию и приведем соответствующие формулы для расчета этого ускорения. Обозначим его ac.

Поскольку центростремительная сила направлена перпендикулярно оси и проходит через нее, то момента она не создает. То есть эта сила не оказывает совершенно никакого влияния на кинематические характеристики вращения. Тем не менее, она создает центростремительное ускорение. Приведем две формулы для его определения:

Таким образом, чем больше угловая скорость и радиус, тем большую силу следует приложить, чтобы удержать тело на круговой траектории. Ярким примером этого физического процесса является занос автомобиля во время поворота. Занос возникает, если центростремительная сила, роль которой играет сила трения, становится меньше, чем центробежная сила (инерционная характеристика).

Кинематика вращения

Три основные кинематические характеристики были перечислены выше в статье. Кинематика вращательного движения твердого тела формулами следующими описывается:

θ = ω*t => ω = const., α = 0;

θ = ω0*t + α*t2/2 => ω = ω0 + α*t, α = const.

В первой строке приведены формулы для равномерного вращения, которое предполагает отсутствие внешнего момента сил, действующего на систему. Во второй строке записаны формулы для равноускоренного движения по окружности.

Отметим, что вращение может происходить не только с положительным ускорением, но и с отрицательным. В этом случае в формулах второй строки следует перед вторым слагаемым поставить знак минус.

Пример решения задачи

На металлический вал в течение 10 секунд действовал момент силы 1000 Н*м. Зная, что момент инерции вала равен 50 кг*м2, необходимо определить угловую скорость, которую придал валу упомянутый момент силы.

Применяя основное уравнение вращения, вычислим ускорение вала:

Поскольку это угловое ускорение действовало на вал в течение времени t = 10 секунд, то для вычисления угловой скорости применяем формулу равноускоренного движения:

Здесь ω0 = 0 (вал не вращался до действия момента сил M).

Подставляем в равенство численные значения величин, получаем:

ω = 1000/50*10 = 200 рад/с.

Чтобы это число перевести в привычные обороты в секунду, необходимо его поделить на 2*pi. Выполнив это действие, получаем, что вал будет вращаться с частотой 31,8 об./с.