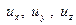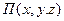Вывод дифференциального уравнения движения жидкости

Дифференциальные уравнения движения идеальной жидкости (уравнения Л. Эйлера)

Дифференциальные уравнения движения идеальной жидкости (уравнения Л. Эйлера)

Дифференциальные уравнения движения идеальной жидкости (уравнения Л. Эйлера). Идеально подходит при выводе дифференциальных уравнений движения Жидкость проигнорирована frictional force. As в результате этого Главным свойством гидростатического давления является независимость От направления можно расширить до гидро Динамическое давление, т. е. Может принимать:px = pv = pv * Во-первых, абсолютное движение, то есть Связь с Землей и движение самой земли Пожалуйста, подумайте. Выберите прямоугольную частицу в потоке жидкости 5d параллелепипед с ребрами длины xx (рис. 8-4).

В рассматриваемом случае, масса Сила тяжести только-еще 80 Поверхностная сила-давление 8Р. Грани. Рассматриваемая частица перемещается в общий случай 4и ИИ. Ускорение a =здесь является производной вектора С ростом-центр частицы во времени. По законам движения Центр инерции Сила должна быть равна произведению массы bm частицы. Йи А = ускорение его центра. 2. Для стабильного движения ТХ + ды (Пу, г) +§к (пт *) =°- (8-22 Дифференциальное уравнение движения для идеальных жидкостей[> 7 Таким образом, уравнение движения является Илиде.

До сих пор неизвестно, существует ли гладкое решение уравнения Эйлера в трёхмерном случае, начиная с заданного момента времени. Людмила Фирмаль

• Чтобы получить уравнение Эйлера, преобразуйте уравнение (8-23). Для этого необходимо сначала спроектировать его на любой оси и Например, по оси x. Что купить： 80 ^ +ЗР, = Прогнозирование оставшихся войск давление на оси x равно нулю. Потому что сила перпендикулярна На оси проекции. Проекция силы тяжести на ось x ЮУ. .Где X-проекция на ось X Только гравитация рения^ .Усилие 8P, гидравлическое для определения разности 6L2 через r динамическое давление центра параллелепипеда .Потому что сила трения равна нулю Р = РХ = Ру = Р * ’ В общем случае гидродинамическое давление Р Функция координат и времени, т . е . п = п (* .г, р, *) .

В этой форме уравнение часто используется для решения различных прикладных задач гидродинамики и газодинамики. Людмила Фирмаль

• Полученные 3 уравнения являются производными Уравнения движения для идеальных жидкостей-уравнения Эйлер .Эти уравнения были получены им в 1755 году .Они правы .Привод как капельницы и газа .Над разницей Социальное уравнение движения неадекватно Количество Больше, чем число известных (p, p7, yi и yi) уравнений .Уравнение второго уравнения закрыть Настой < ?= sopz1), уравнение является непрерывным СТИ (8-21) .Для изучения движения газового потока (п ф сопз ! Необходимо пополнить систему 5-й формулой .Клапейрон-выведено уравнение состояния Менделеева.

Возьмем непрерывное уравнение в виде (8-20) .1 см .сноски на стр . 33 .L .уравнения Эйлера в натуральном виде 19 Уравнение Эйлера абсолютного движения, полученное выше Ния могут быть представлены в векторном виде .(П) =^, (8-26 Где$ вектор ускорения силы тяжести .§Gas1 (p) гидродинамический градиент давления (см .сноску Страница 38) .Правильность этой формы уравнений легко проверить Спроектируйте его по координатным осям и получите уравнение в качестве его заднего Эйлера в координатной форме .Уравнения Эйлера также могут быть использованы для следующих целей.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Уравнение Бернулли. Дифференциальные уравнения движения идеальной жидкости

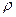
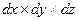
В движущейся идеальной жидкости, плотность которой , выделим элементарный параллелепипед размерами и запишем дифференциальные уравнения движения этого объема жидкости в координатной форме, рассматривая его как материальную точку.

На элемент действуют составляющие сил давления и массовых сил, интенсивность которых на единицу массы по направлению осей равна 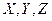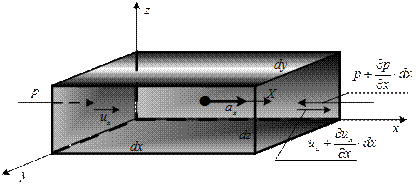(рис. 6.1).

Рис. 6.1

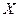
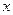
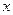
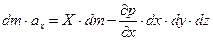На рисунке показаны только составляющая массовых сил по оси , давление на гранях перпендикулярных оси и составляющая ускорения по оси , что позволяет записать уравнение движения выделенного объема в направлении оси

.

(6.1)

Так как масса элементарного объема легко определяется через массовую плотность

,

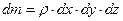(6.2)

то после деления обеих частей уравнения (6.1) на (6.2), получаем

.

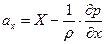(6.3)

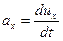
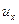
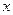
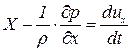С учетом того, что , где – проекция скорости элементарного объема на ось , уравнение (6.3) принимает вид

.

(6.4)

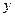
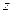
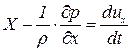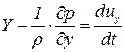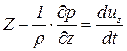Действуя аналогично можно получить уравнения движения выделенного элемента в направлении осей и . Таким образом система дифференциальных уравнений движения идеальной жидкости в декартовой прямоугольной системе координат имеет вид

, ,

(6.5)

Уравнение Бернулли для установившегося движения при действии

Последовательно умножим уравнения (6.5) на и сложим полученные результаты

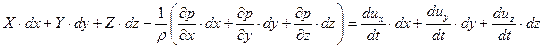(6.6)

При установившемся движении

,

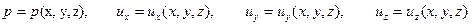(6.7)

тогда в рассматриваемый момент времени

.

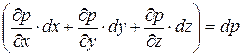(6.8)

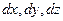
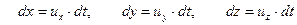В движущейся жидкости размеры элементарного параллелепипеда можно определить через составляющие скорости частицы

.

(6.9)

С учетом (6.9) правая часть уравнения (6.6) приводится к виду

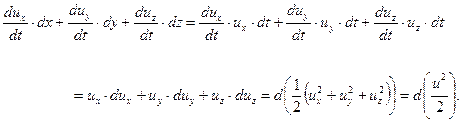(6.10)

Если движение жидкости происходит в потенциальном силовом поле, то составляющие интенсивности массовых сил определяются через потенциальную энергию этого поля, приведенную к единице массы

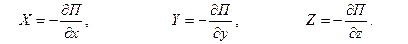(6.11)

Принимая во внимание (6.11), первое слагаемое в левой части уравнения (6.6) можно записать так

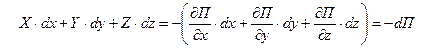(6.12)

С учетом (6.8), (6.10), (6.12) уравнение (6.6) принимает следующий вид

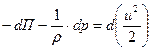(6.13)

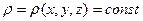
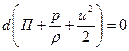Так как идеальная жидкость – это несжимаемая жидкость, и (6.13) можно записать в виде

,

(6.14)

.

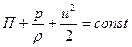(6.15)

Уравнение (6.15) и является уравнением Бернулли для элементарной струйки идеальной жидкости при установившемся движении, когда элементарную струйку можно отождествлять с линией тока. Для различных линий тока значения константы в уравнении (6.15) будут разными.

Замечание. Более детальное изучение движения частицы жидкости позволяет установить, что при изменении положения в пространстве происходит изменение ее формы и объема. Движение можно представить как сумму трех движений: поступательного (вместе с полюсом), деформационного (за счет изменения размеров) и вращательного (вокруг мгновенной оси, проходящей через полюс).

По характеру движения частиц различаютвихревое и потенциальное движения.

Вихревым движением называют такое движение, при котором движущиеся частицы жидкости вращаются вокруг осей, проходящих через их полюсы. Вихревое движение характеризуется вихревыми линиями – линиями, в каждой точке которых касательная совпадает с вектором угловой скорости .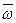

Движение, при котором такое вращение отсутствует, называется безвихревым или потенциальным движением.

Уравнение Бернулли справедливо:

· вдоль линии тока;

· на вихревых линиях;

· при винтовом движении, когда векторы линейной и угловой скоростей параллельны (линия тока совпадает с вихревой линией);

· при потенциальном движении;

· при статическом равновесии жидкости.

Проведем детальное рассмотрение параметров, характеризующих движение жидкой частицы, но ограничимся только движением в плоскости xy (рис. 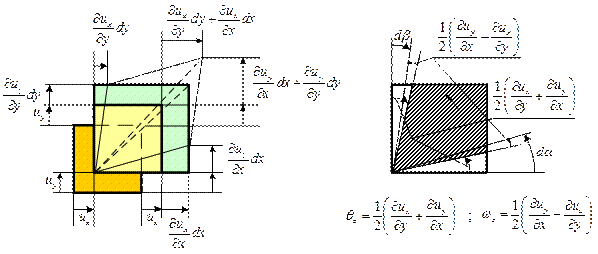6.2).

Рис. 6.2

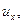
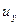
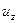
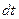
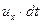
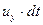
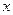
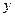
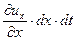Частица жидкости в форме прямоугольного параллелепипеда (рис. 6.1) имеет в точке О локальную скорость, составляющие которой равны , . Если О полюс, движущейся частицы, за время сместится на расстояние в направлении оси x и на расстояние в направлении оси y, то за счет приращения скорости в направлении осей и ребра частицы получат абсолютные удлинения: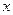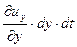

— по оси ; — по оси .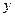

(6.16)

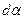
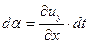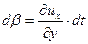Кроме деформаций удлинения частица в окрестности точки О претерпевает деформации сдвига, характеризуемые углами и

; .

(6.17)

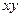
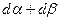
Суммарную деформацию сдвига в плоскости равную можно разложить на две составляющие:

деформацию сдвига, характеризуемую углами

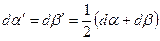(6.18)

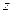
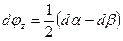и поворот частицы относительно оси , проходящей через полюс О, на угол

(6.19)

Следовательно, изменение положения и формы частицы в плоскости 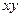характеризуется:

скоростями линейных относительных деформаций

,

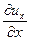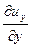(6.20)

скоростью деформации сдвига

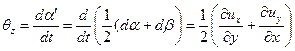(6.21)

угловой скоростью вращения частицы относительно оси

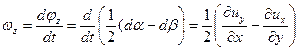(6.22)

В общем случае деформационное движение частицы характеризуется:

скоростями линейных деформаций

, , ;

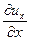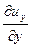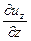(6.23)

скоростями угловых деформаций

;

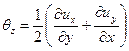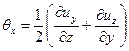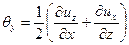(6.24)

составляющими мгновенных угловых скоростей

;

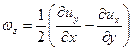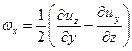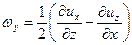(6.25)

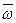
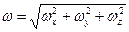Вектор мгновенной угловой скорости направлен по нормали к плоскости в которой происходит вращение, а его модуль легко определяется по составляющим

.

(6.26)

С направлением вектора 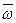связано определение вихревой линии – линии, в каждой точке которой вектор угловой скорости совпадает с направлением касательной к этой линии (рис.6.3).

Рис. 6.3

Дифференциальное уравнение вихревой линии имеет вид

,

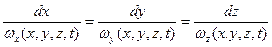(6.27)

где 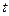рассматривается как параметр.

Дифференциальные уравнения движения жидкости

Это уравнение векторное и в проекциях на оси выбранной системы координат дает три уравнения. Вывод дифференциального уравнения движения в общем случае требует громоздких математических выкладок. Поэтому для упрощения вывода рассмотрим одномерное течение жидкости. Выделим в потоке вязкой жидкости, как показано на рис. 2.3, элементарный объем с размерами ребер dx, dy и dz.

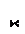
Скорость в потоке изменяется только в направлении оси Оу. Силы, действующие на элемент жидкости, можно разделить на массовые (или объемные) и поверхностные. К массовым силам относятся сила тяжести, центробежная сила и электромагнитные силы. Мы в дальнейшем будем учитывать только силу тяжести. К поверхностным силам относятся силы давления и силы трения. Найдем проекции этих сил на ось Ох.

Сила тяжести равна произведению массы элемента на проекцию ускорения свободного падения на ось Ох

Равнодействующая сил давления в проекции на ось Ох равна

Равнодействующая сил трения с учетом уравнения (1.11) в проекции на ось Ох составляет

Суммируя получим проекцию равнодействующей всех сил на ось Ох, приложенных к объему

(а)

Согласно второму закону механики эта равнодействующая равна произведению массы элемента на проекцию ее ускорения на ось Ох и учитывает силы инерции

(б)

Приравнивая правые части (а) и (б) и производя сокращения, получим уравнение движения вдоль оси Ох

В общем случае трехмерного движения несжимаемой жидкости уравнение движения в проекциях на оси Ox, Oy и Oz соответственно имеет вид:

(2.5)

(2.6)

(2.7)

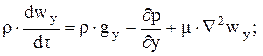
Или в векторном виде

(2.8)

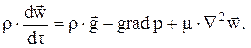
Уравнения (2.5) – (2.8) называют уравнениями Навье-Стокса. Член, стоящий в левой части уравнений, представляет собой полную производную от скорости по времени

(2.9)

где i соответственно x, y, z.

Первые слагаемые в правой части (2.9) характеризуют локальное изменение скорости во времени в какой-либо точке жидкости. Остальные три слагаемых в правой части характеризуют изменение скорости при переходе от точки к точке. Такая полная производная называется субстанциональной производной. Уравнения движения получены при постоянных теплофизических свойствах жидкости. В то же время свободное движение жидкости (естественная конвекция) определяется разностью плотностей холодных и нагретых частиц жидкости. В общем случае при r¹const необходимо учитывать и энергию деформации жидкости. Поэтому ограничимся приближенным учетом переменности плотности в слагаемом, связанным с силой тяжести в уравнениях движения. Пусть плотность линейно зависит от температуры

где r и r₀ – плотности, соответствующие температурам t и t₀;

J=t-t₀; t₀ – некоторая фиксированная температура (точка отсчета).

Подставляя это значение плотности в первое слагаемое правой части (2.8), получим приближенно

Первое слагаемое правой части можно трактовать как сумму силы тяжести , взятой при определенной плотности, и подъемной (архимедовой) силы . Член можно представить как градиент гидростатического давления р₀ в покоящейся жидкости с плотностью r₀. Тогда вместо можно написать grad p₁, где p₁=p-p₀. При такой замене приближенное векторное уравнение движения будет описывать и естественное движение жидкости (естественную конвекцию)

(2.10)

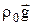
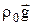
Таким образом, для задач теплообмена система дифференциальных уравнений сохранения массы (уравнение неразрывности или сплошности), энергии и движения в проекциях на координатные оси оказывается замкнутой. Эта система уравнений в принципе позволяет определить в движущейся жидкости поле температуры T=T(x, y, z, t), поле давлений p=p(x, y, z, t) и поля проекций скоростей w_x=w_x(x, y, z, t), w_y=w_y(x, y, z, t), w_z=w_z(x, y, z, t).

Для задач массообмена, не осложненных теплообменом (в изотермических условиях), уравнение энергии в этой системе заменяется уравнением сохранения массы i-го компонента смеси. Вывод этого уравнения, которое называют уравнением массообмена, аналогичен выводу дифференциального уравнения сохранения энергии при q_V=0 и имеет вид

(2.11)

где mi=Ci/r – относительная массовая концентрация i-го компонента.

В случаях, когда массообмен осложнен теплообменом (в неизотермических условиях), кроме уравнения (2.11), необходимо уравнение сохранения энергии. Однако вывод этого уравнения с учетом (1.13) усложняется. Для двух компонентной (бинарной) смеси оно имеет вид

(2.12)

Из этого уравнения видно, что, если удельные изобарные теплоемкости компонентов смеси равны с_р1=с_р2, то результирующий перенос энтальпии отсутствует, и это уравнение переходит в ранее полученное уравнение (2.4).